An affordable explanation of the wave function collapse algorithm
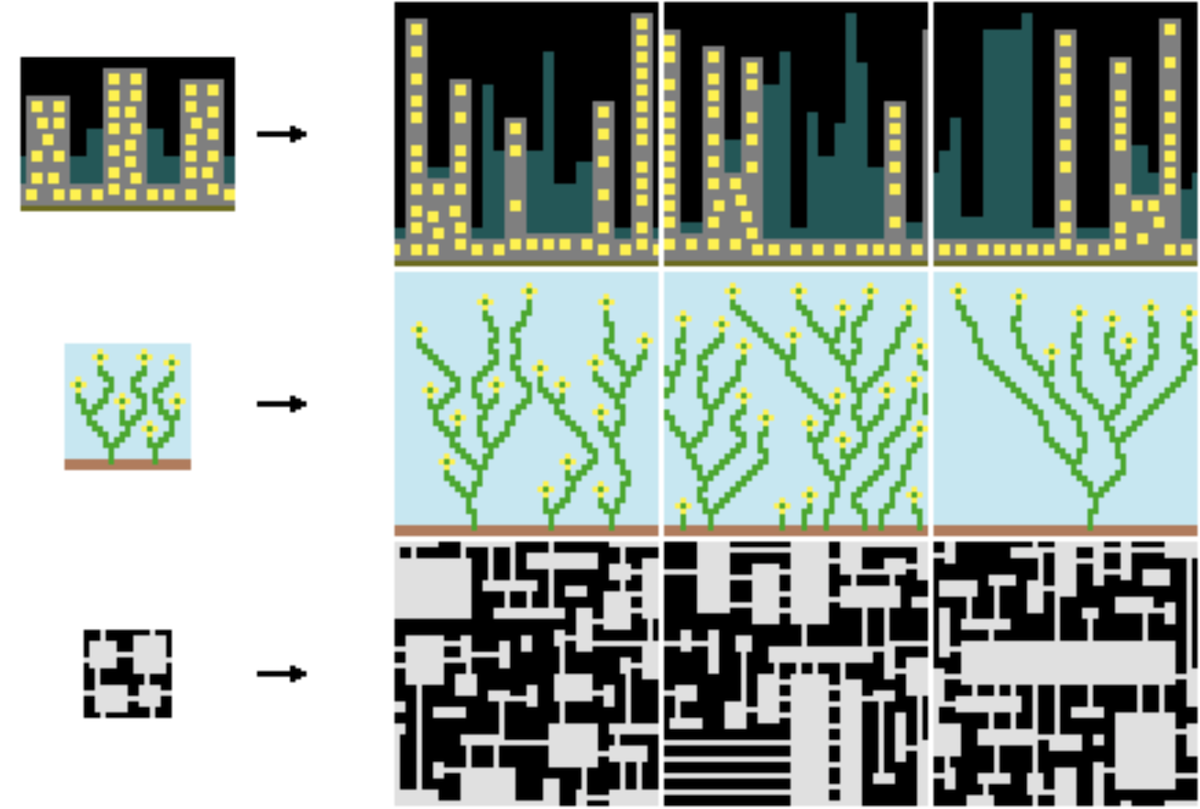
The Wavefunction Collapse Algorithm teaches a computer to improvise. At the input, it receives archetypal data and creates procedurally generated data similar to the original.
( Source )
Most often it is used to create images, but it can also build cities , skateparks and write awful poems .
')

( Source )
The collapse of the wave function is a very independent-minded algorithm that requires virtually no help or instructions from outside. You only need an example of the style that you want to achieve, and he will do the rest. Despite his self-sufficiency, he is surprisingly simple. It does not use any neural networks, random forests, or anything else that resembles machine learning. If you deal with the idea, it will become very understandable and intuitive for you.
Most implementations and explanations of the collapse of the wave function are a complete, speed-optimized version of the algorithm. Of course, all of them are important and necessary, but it is difficult to understand them from scratch. In this post, I will explain everything in a simple language that I understand, focusing on the limited version of Wavefunction, which I called Even Simpler Tiled Model . In addition, I posted an example implementation of ESTM on Github . The code in it is inefficient and slow, but very readable and commented in detail. As soon as you understand the technology underlying ESTM, you will become closer to understanding more complex versions of the algorithm. If you want to understand the wave function collapse algorithm, then this article will be a good start.
Let's start with the story.
Imagine that you are planning your wedding. In addition to the selection of jewelry and music, you need to create a seating plan for guests for dinner. Your family likes to argue and be naughty, so it can be difficult. A father cannot sit closer than two tables from his mother. A cousin becomes lonely if she does not sit with another cousin. And it’s better not to plant Uncle Roy next to the environmentally-friendly members of your partner’s family. There is only 5 hours left before the arrival of food, so you decide to attack this stubborn task using the wave function collapse algorithm.
You start with a long list of rules and an empty seating plan.
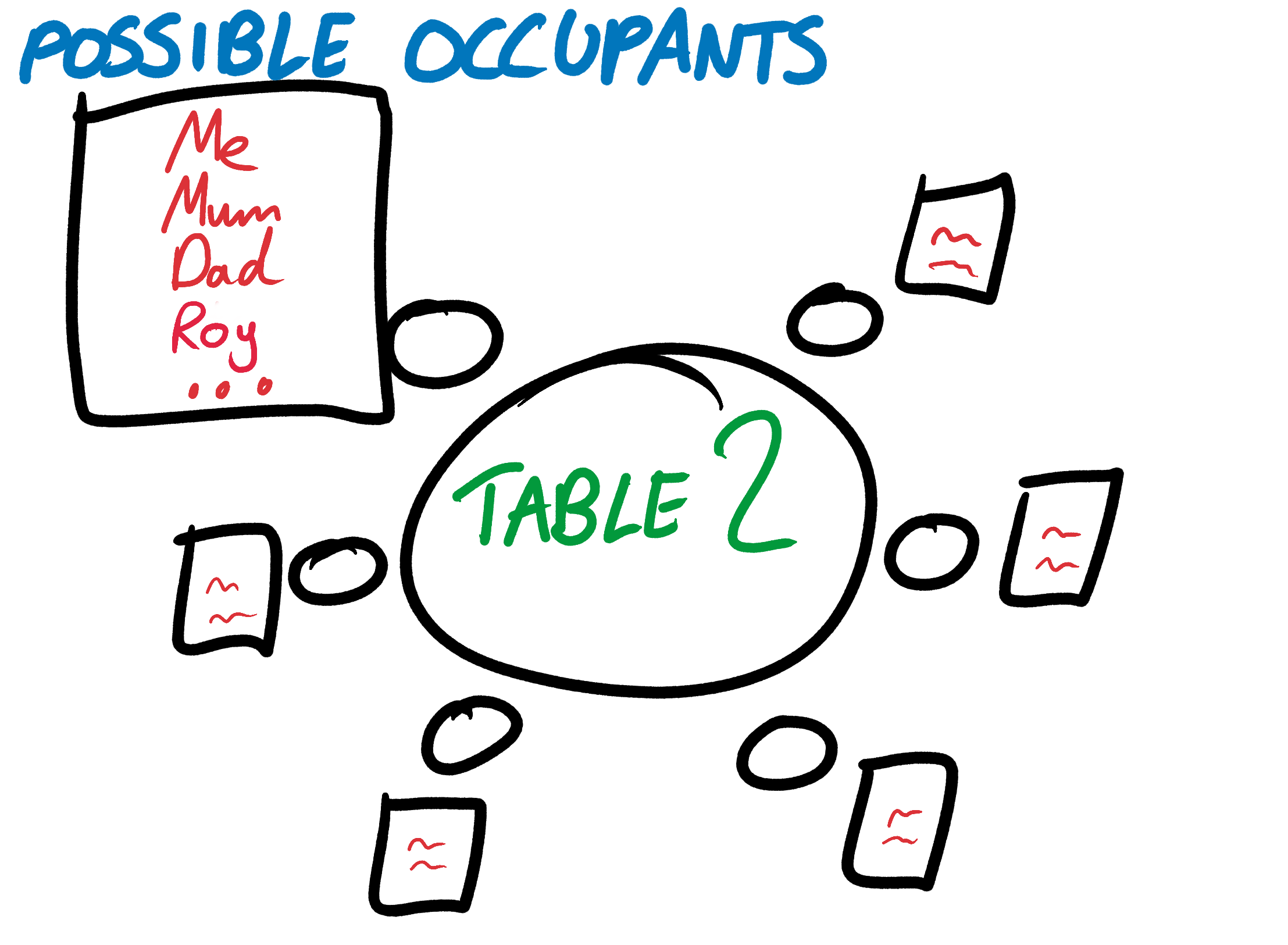
You create the original wave function of the plan. She ties each chair to a list of people who can sit on it. While any person can sit on any chair. The wave function of seating guests begins with a complete superposition (the concept is borrowed from quantum physics) of each possible scheme.
Schrödinger's cat was dead and alive at the same time, until someone opened the box and checked; your plan is at the same time every possible scheme until you put things in order. A complete superposition is a useful theoretical construct, but it will not help your grandmother figure out where she needs to sit. You need to bring the wave function of the guests' location to a single certain state, which can then be turned into ordinary, non-quantum name cards.
We begin to do this by performing the collapse of the wave function for one chair. We select a chair, look at the list of people who can sit on it, and randomly assign it to one of them. In this case, the wave function of the stool becomes collapsed.
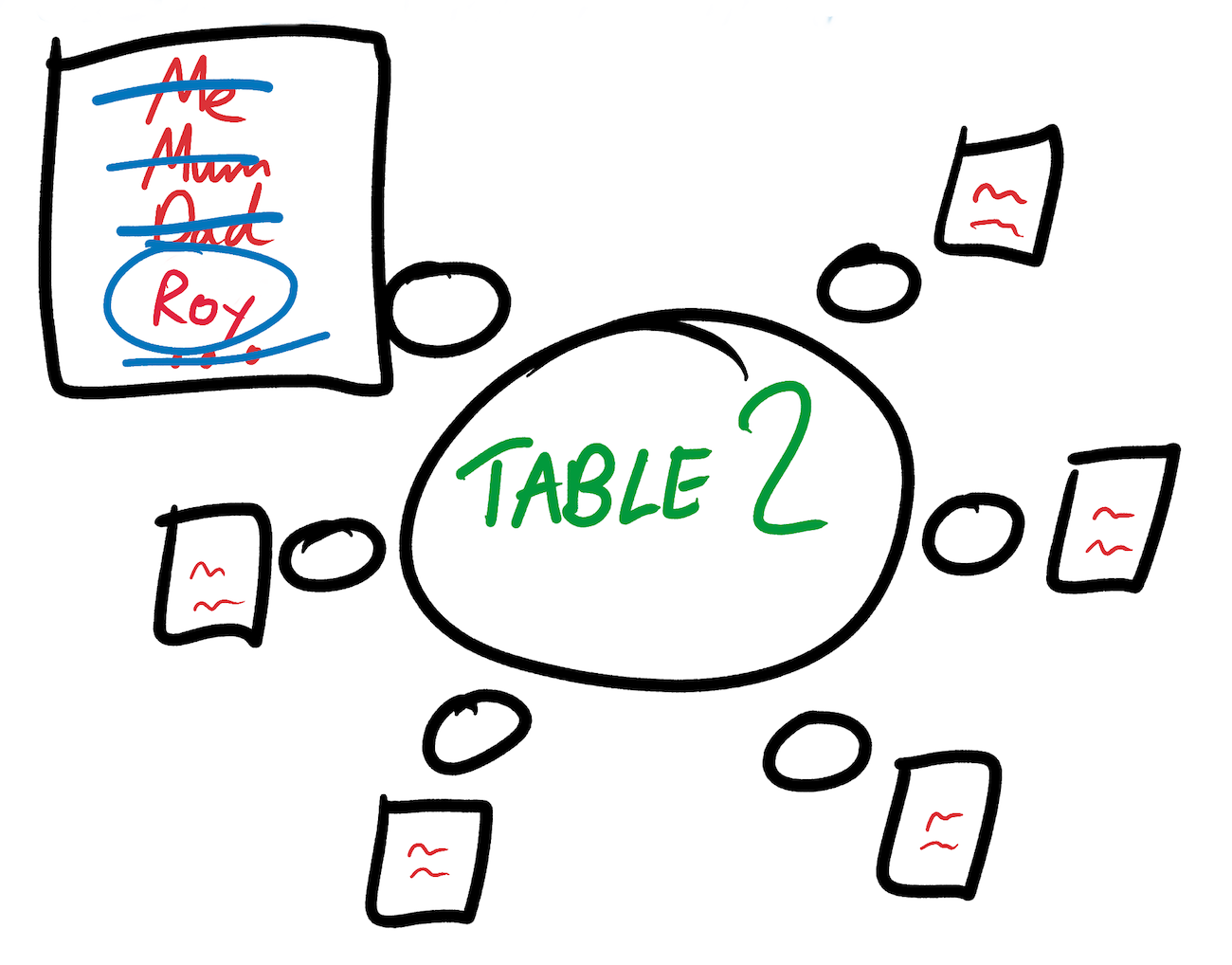
This choice has consequences that apply to the wave functions of the remaining chairs. If Uncle Roy is sitting at table 2, then cousin Frank and Michelle Obama (a friend of your partner's family) will definitely not be next to him. And if Michelle does not sit at table 2, then Barack will not be behind him either. We are updating the wave function of the location plan by deleting people from the lists of possible candidates.
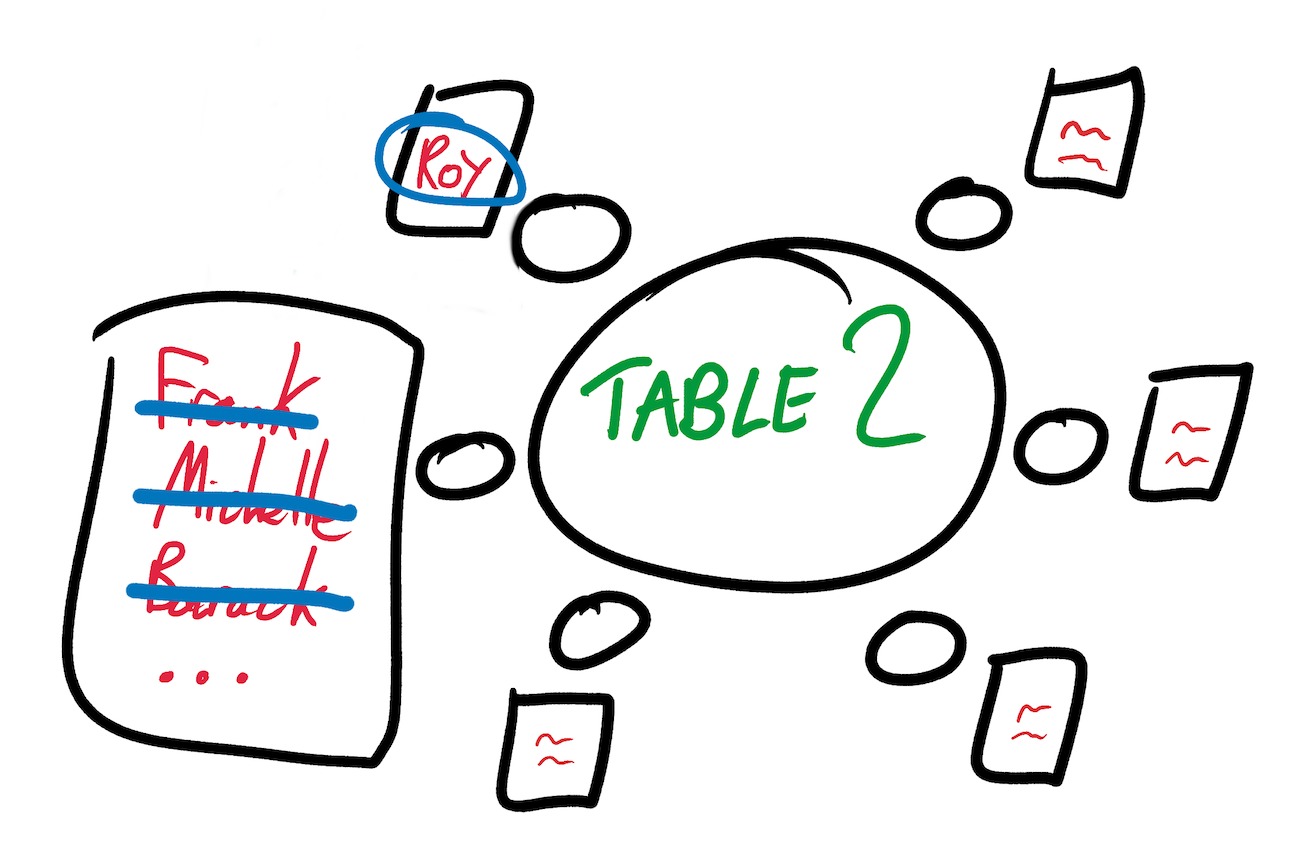
As soon as the vibrations settle, we repeat this process. We select another chair with several possible candidates and collapse its wave function, randomly choosing one of the people acceptable for it. Again, we extend the vibrations caused by this choice to the rest of the plan, removing people from the wave function of the chair if they can no longer sit on it.
We repeat this process either until the wave function collapses (that is, exactly 1 sitting person remains in it), or until we reach a contradiction . Contradiction is a chair that no one can sit on, because they were all expelled due to previous elections. The contradiction makes the impossibility of the collapse of the entire wave function.
If you have reached a contradiction, then the easiest way is to start over. Discard all previous work, find a new empty plan and start the algorithm again, completing the collapse of the wave function for another random chair. You can also implement a backtracking system that allows you to cancel a single choice, rather than immediately abandon everything ("what if Sheila is transferred to chair 54?").
After a few false starts, you will finally reach a completely collapsed state in which each chair is assigned to exactly one person and all the rules are followed. Done!
This is not a theoretical example. You really can implement the option of collapse of the wave function, which will create a seating plan for guests for the wedding. However, in the more traditional Wavefunction Collapse, we usually try not to seat people at the wedding, but to arrange the pixels in the output image. However, the process will be very similar. We teach the algorithm a set of rules that the output should satisfy. We initialize the wave function. We perform the collapse of one element and extend the consequences to the rest of the wave function. And we continue to do so, either until the wave function completely collapses, or until we reach a contradiction.
The traditional collapse of the wave function differs from the wedding collapse in the way we teach the algorithm the rules that it must follow. In the wedding version, we had to write down the rules ourselves. But in the traditional version, we just give the algorithm an example image, and based on it, the algorithm creates the rest. He parses an example, analyzes its patterns and finds out how pixels or tiles should line up.
Let's start researching the real collapse of a wave function by looking at a simple special case, which
In the Simple Tiled Model, input and output images are constructed from a small number of predefined tiles, and each square in the output image is limited to only its four nearest neighbors. For example, suppose we generate random worlds for a two-dimensional game with a top view. We can have tiles for land, coast and sea, as well as a set of rules such as “the coast can be near the sea”, “land can be near the coast” and “the sea can be near another sea”.
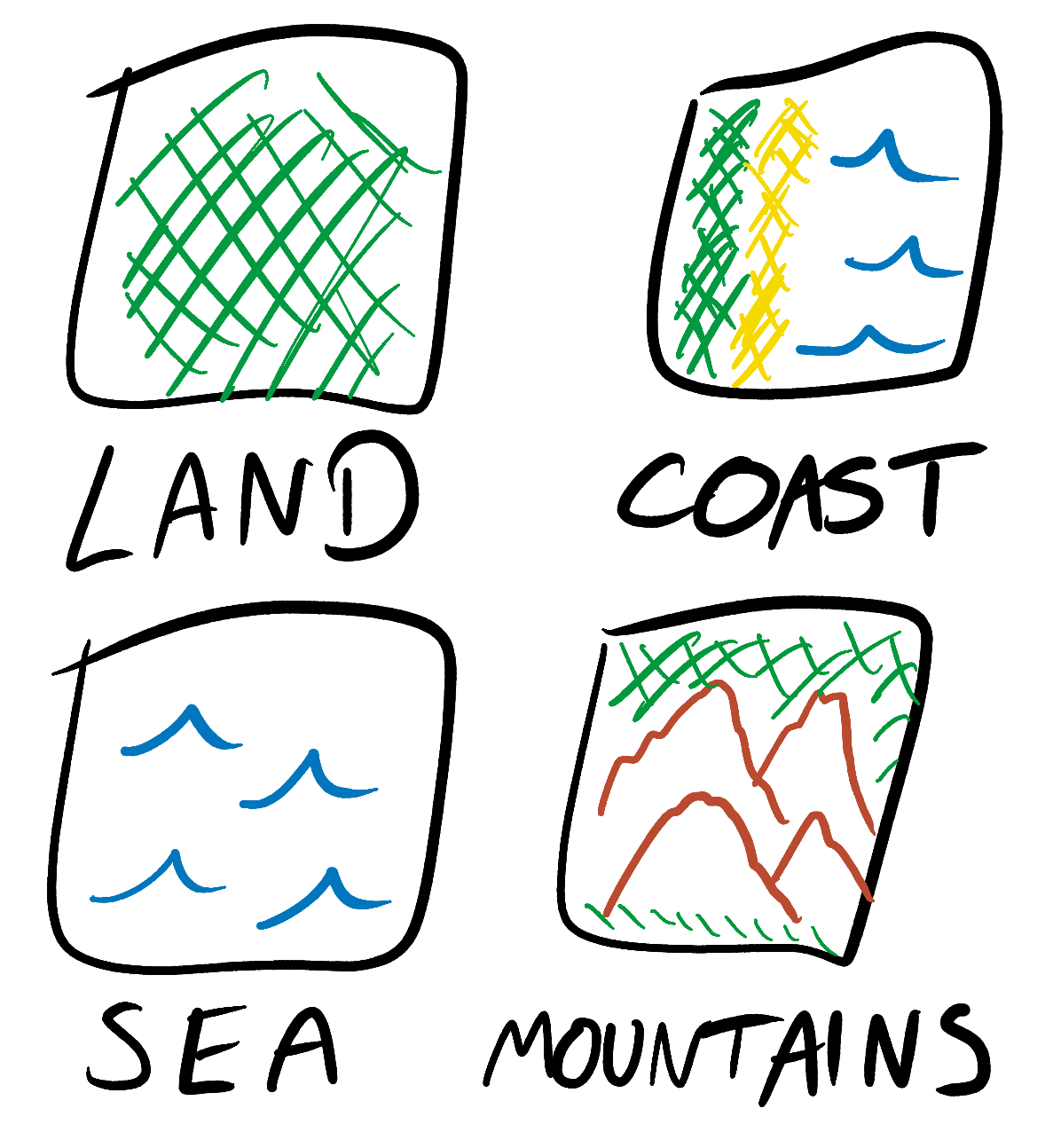
The Simple Tiled Model takes into account the symmetry and rotation of its tiles. For example, land may be near the coast, but only in the correct orientation.
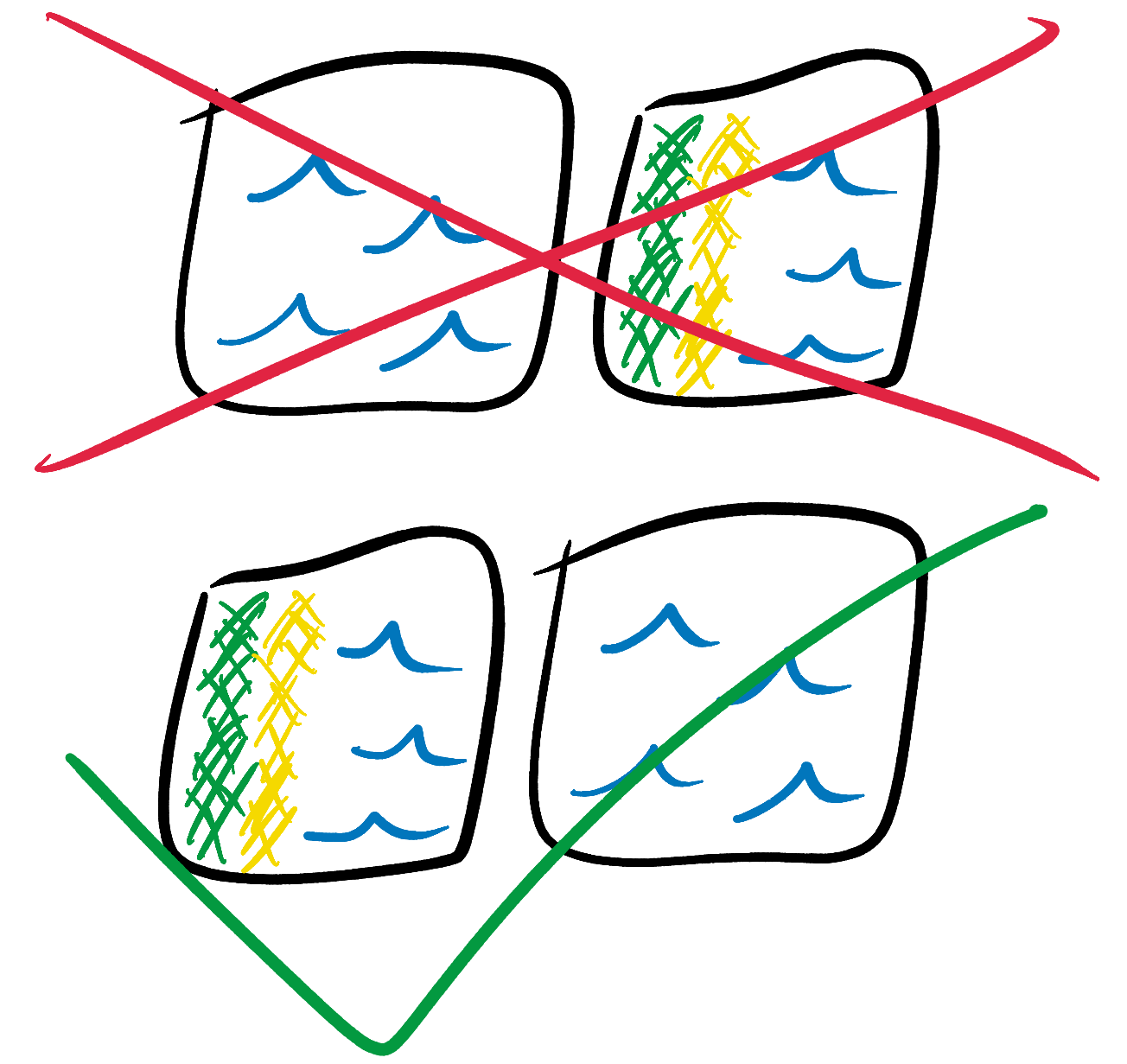
This symmetry processing provides better output images, but complicates the code. To keep things simple, let's look at an even simpler form of wave function collapse, which I called Even Simpler Tiled Model .
Even the Simpler Tiled Model (“an even simpler tile model”) is similar to the Simple Tiled Model, but its tiles do not have symmetry properties. Each tile is one pixel of the same color, that is, we will not be able to confuse their edges in any way.
Even Simpler Tiled Model rules determine which tiles can be placed next to each other and in which orientation. Each rule is a tuple of three elements (3-tuple): two tiles and a direction. For example,

If you want the
As I said above, we do not need to create a list of all these rules ourselves. The collapse of the wave function can create a set of rules for Even Simpler Tile Model by parsing an example image and collecting a list of all 3-tuple it contains.
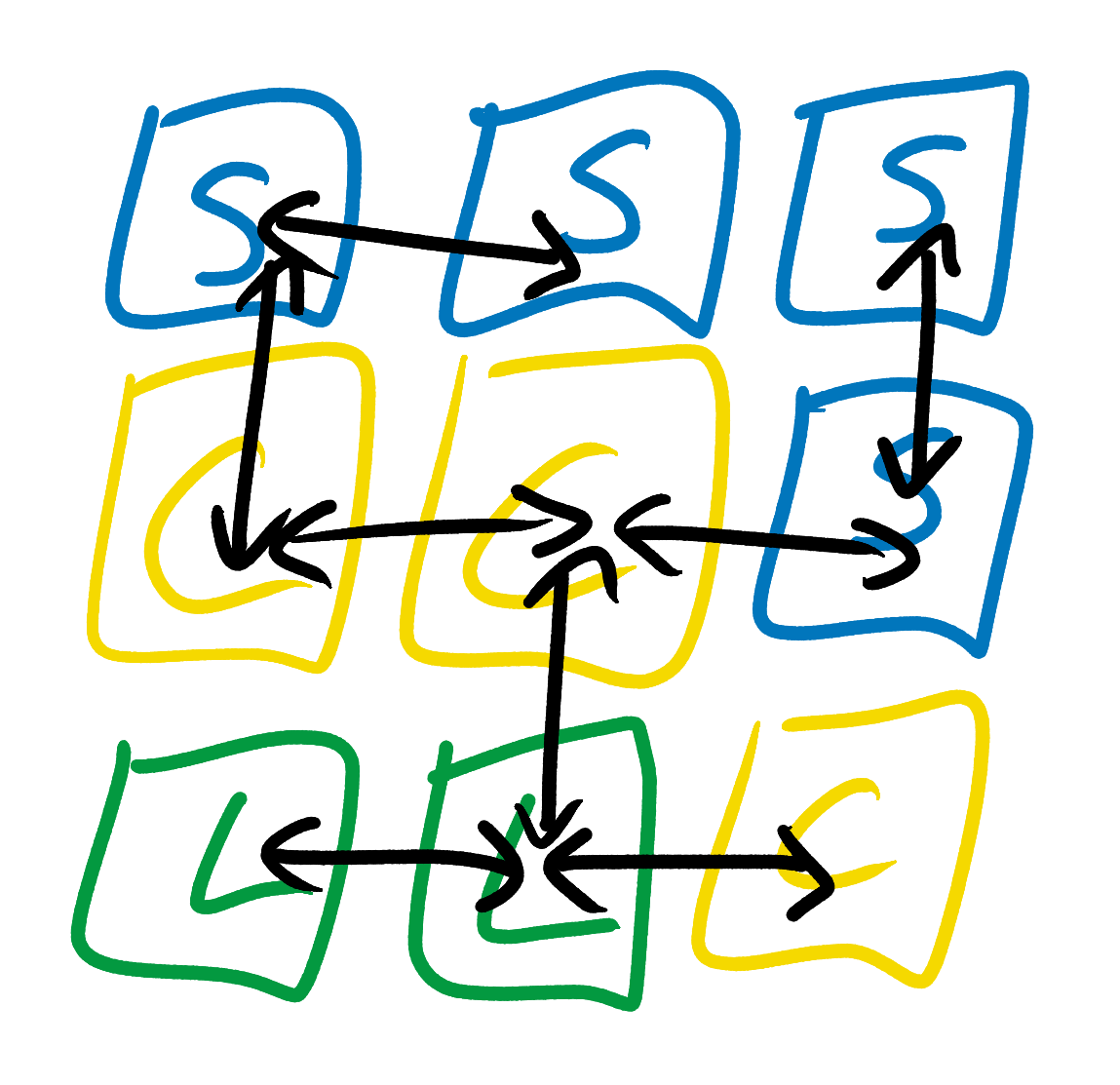
Having examined the example image shown above, Even Simpler Tiled Model notices that the sea tiles can only be under or to the side of the coast tiles, or anywhere near other sea tiles. She also notes that coast tiles can be located next to land, sea, or other coast tiles, but only above sea tiles and under land tiles. She does not try to derive any more complex rules, for example, "sea tiles should be near at least one sea tile" or "each island must contain at least one land tile." None of the tiles can affect the fact that some types of tiles can or cannot be located two or more squares from them. This is similar to a wedding plan model, with the only rule: “X can sit next to Y”.
When analyzing the incoming image, we also need to record the frequency with which each of the tiles meets. Later, we use these numbers as weights when choosing the wave function of the square whose collapse needs to be performed, as well as when choosing the tile assigned to the square when it is collapsed.
Having learned the rules that the output image must adhere to, we are ready to build the collapse of the wave function of the output image.
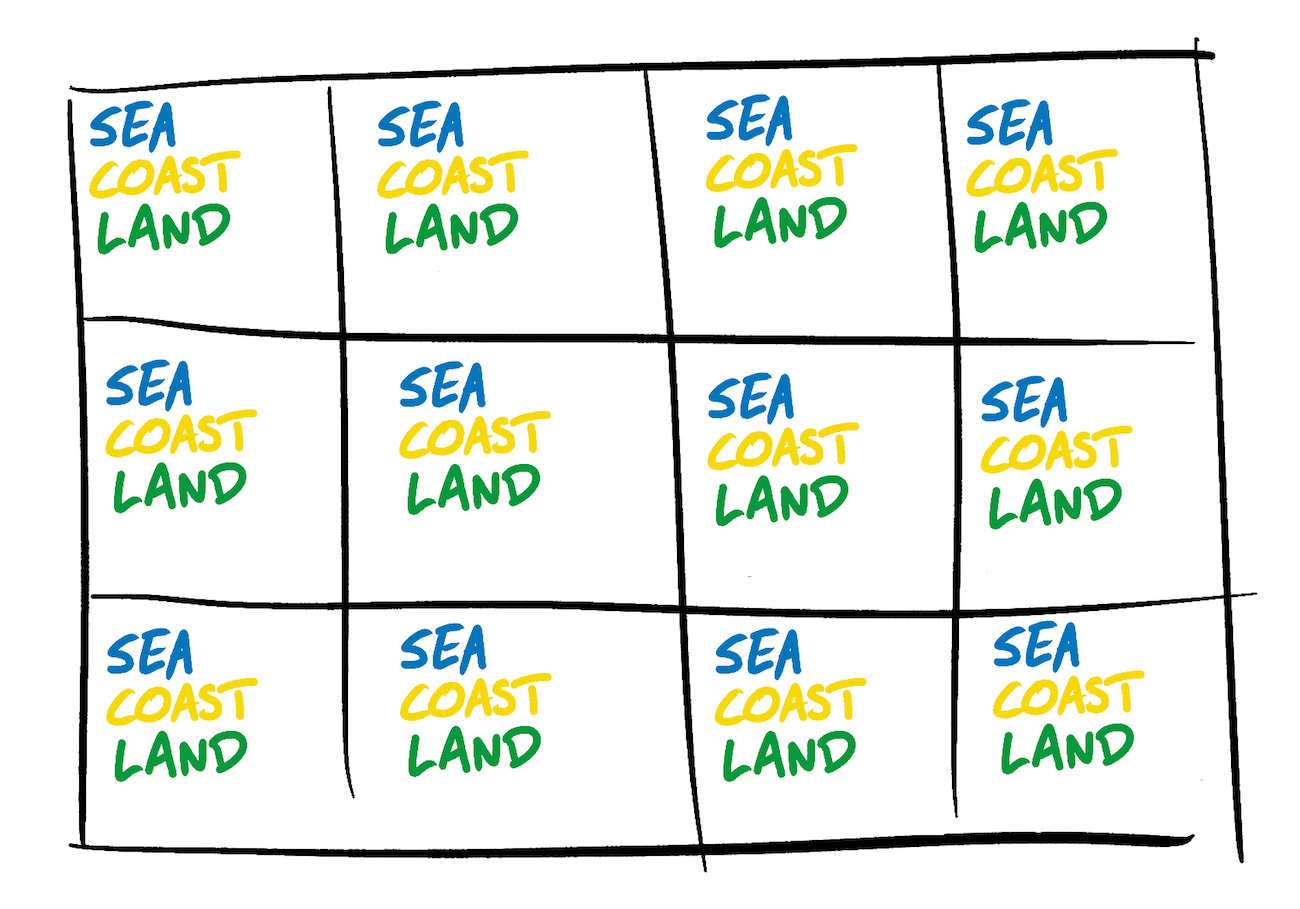
As in the wedding example, we begin the process of collapsing with a wave function in which each square of the output image is in a superposition of each type of tile.
We begin by choosing a square whose wave function will collapse. In the wedding example, this choice was made by chance. However, as
For example, in the Even Simpler Tile Model, a square without information about the surrounding squares is unlimited and can become any tile. Therefore, it has a very high entropy. But a square around which several squares have already collapsed can have a choice of only 2 tiles.
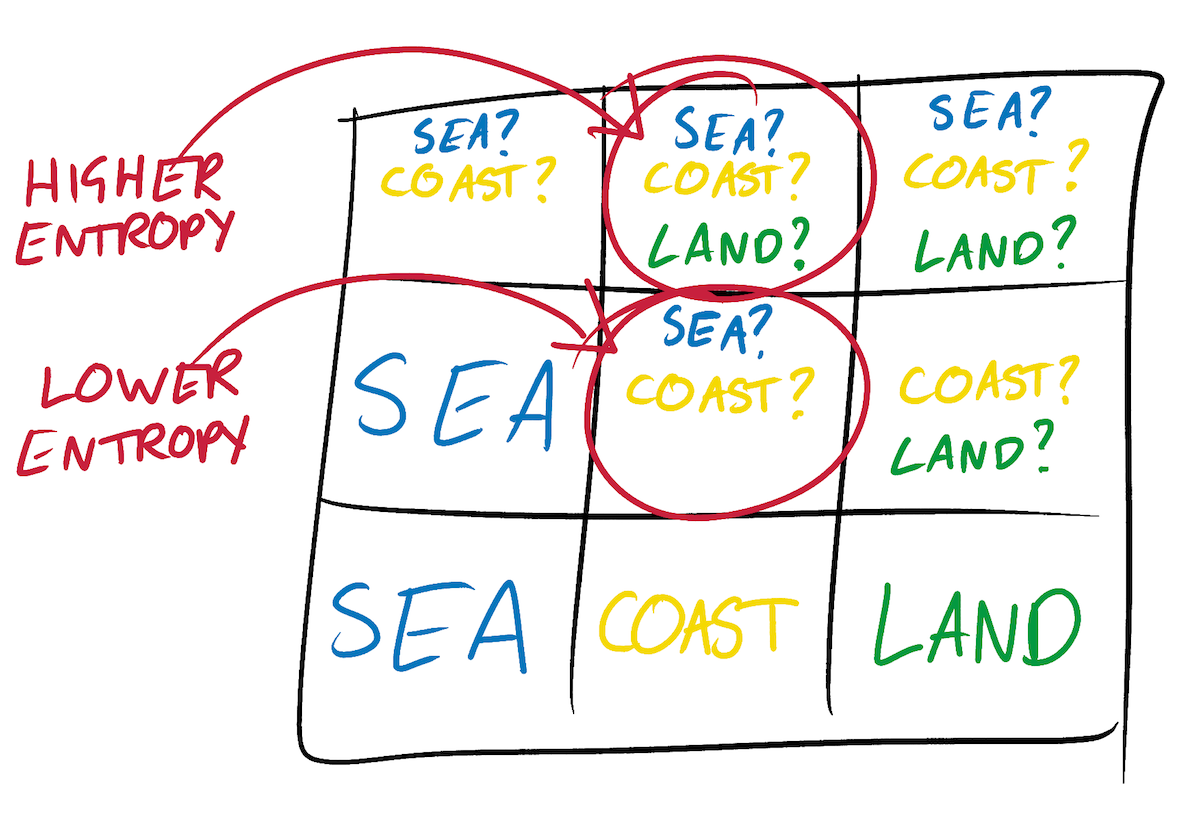
The wave function of the central square in the figure above did not completely collapse, but we already know that it cannot be a land tile. However, it is already limited, which means it has an entropy lower than that of the upper right square, which can still be land, sea or coast.
It is such limited tiles with low entropy that people usually pay attention to when they manually solve such problems. Even if you do not use the collapse of the wave function to create a plan for accommodating guests at the wedding and will draw it up yourself, you will still focus on those areas of the plan that already have the greatest number of restrictions. You will not put Dwayne at table 1, and then randomly jump to get Katie at table 7 (which is empty so far). You first put Dwayne, then you will figure out who can sit next to him, then who can sit next to this person, and so on. I have not yet seen the rationale for this, but my intuition says that using this heuristic of minimal entropy is likely to produce less contradictions than if you randomly select squares for collapse.
The Shannon formula is used as the entropy formula in the wave function collapse algorithm. It uses the weights of the tiles that we parsed from the incoming image in the previous step:
Having calculated the square of the wave function with the smallest entropy, we collapse its wave function. We do this by randomly selecting one of the tiles that are still available for the square, weighted by the weights of the tiles that we parsed from the incoming image. Weights are used because it provides a more realistic output image. Suppose the wave function of a square reports that it can be land or coast. We do not always have to choose one of the options with a probability of 50%. If the input image has more land tiles than the coast, then we should reflect this advantage in the output image. This is realized using simple global weights. If in the example image there are
Then we extend the consequences of the choice to the rest of the wave function of the output (“if that tile turned out to be the sea, then this tile cannot be land, that is, this cannot be the coast”). When all these tremors have settled, we repeat the process using the minimum entropy heuristic to select the next collapsing tile. We repeat this collapse-propagation cycle, either until the entire wave function of the output image completely collapses and we can return the result, or until we reach a contradiction and return an error.
As a result, we created a world (or mistake).
Having dealt with the Even Simpler Tiled Model, you are ready to climb the ladder of power and complexity of the algorithm. Start with the Simple Tiled Model that we mentioned at the beginning of this post, then go on to the full Overlapping Model. In the Overlapping Model, tiles or pixels affect each other from a distance. If you understand such things, then
Wavefunction Collapse can even take into account additional restrictions, for example, “this tile must be sea” or “this pixel must be red” or “there can be only one monster in the output”. All this is described by the README of the main project . You can also study the speed optimizations made to the full implementation. It is not necessary to recalculate the entropy of each square in each iteration, and the dissemination of information by the wave function can be done much faster. These aspects become more important as the size of the output images increases.
The collapse of the wave function is a beautiful and powerful tool that is worth mastering. Think about it the next time you plan a wedding or generate a procedural world.

( Source )
Most often it is used to create images, but it can also build cities , skateparks and write awful poems .
')

( Source )
The collapse of the wave function is a very independent-minded algorithm that requires virtually no help or instructions from outside. You only need an example of the style that you want to achieve, and he will do the rest. Despite his self-sufficiency, he is surprisingly simple. It does not use any neural networks, random forests, or anything else that resembles machine learning. If you deal with the idea, it will become very understandable and intuitive for you.
Most implementations and explanations of the collapse of the wave function are a complete, speed-optimized version of the algorithm. Of course, all of them are important and necessary, but it is difficult to understand them from scratch. In this post, I will explain everything in a simple language that I understand, focusing on the limited version of Wavefunction, which I called Even Simpler Tiled Model . In addition, I posted an example implementation of ESTM on Github . The code in it is inefficient and slow, but very readable and commented in detail. As soon as you understand the technology underlying ESTM, you will become closer to understanding more complex versions of the algorithm. If you want to understand the wave function collapse algorithm, then this article will be a good start.
Let's start with the story.
Wedding
Imagine that you are planning your wedding. In addition to the selection of jewelry and music, you need to create a seating plan for guests for dinner. Your family likes to argue and be naughty, so it can be difficult. A father cannot sit closer than two tables from his mother. A cousin becomes lonely if she does not sit with another cousin. And it’s better not to plant Uncle Roy next to the environmentally-friendly members of your partner’s family. There is only 5 hours left before the arrival of food, so you decide to attack this stubborn task using the wave function collapse algorithm.
You start with a long list of rules and an empty seating plan.

You create the original wave function of the plan. She ties each chair to a list of people who can sit on it. While any person can sit on any chair. The wave function of seating guests begins with a complete superposition (the concept is borrowed from quantum physics) of each possible scheme.

Schrödinger's cat was dead and alive at the same time, until someone opened the box and checked; your plan is at the same time every possible scheme until you put things in order. A complete superposition is a useful theoretical construct, but it will not help your grandmother figure out where she needs to sit. You need to bring the wave function of the guests' location to a single certain state, which can then be turned into ordinary, non-quantum name cards.
We begin to do this by performing the collapse of the wave function for one chair. We select a chair, look at the list of people who can sit on it, and randomly assign it to one of them. In this case, the wave function of the stool becomes collapsed.

This choice has consequences that apply to the wave functions of the remaining chairs. If Uncle Roy is sitting at table 2, then cousin Frank and Michelle Obama (a friend of your partner's family) will definitely not be next to him. And if Michelle does not sit at table 2, then Barack will not be behind him either. We are updating the wave function of the location plan by deleting people from the lists of possible candidates.

As soon as the vibrations settle, we repeat this process. We select another chair with several possible candidates and collapse its wave function, randomly choosing one of the people acceptable for it. Again, we extend the vibrations caused by this choice to the rest of the plan, removing people from the wave function of the chair if they can no longer sit on it.
We repeat this process either until the wave function collapses (that is, exactly 1 sitting person remains in it), or until we reach a contradiction . Contradiction is a chair that no one can sit on, because they were all expelled due to previous elections. The contradiction makes the impossibility of the collapse of the entire wave function.
If you have reached a contradiction, then the easiest way is to start over. Discard all previous work, find a new empty plan and start the algorithm again, completing the collapse of the wave function for another random chair. You can also implement a backtracking system that allows you to cancel a single choice, rather than immediately abandon everything ("what if Sheila is transferred to chair 54?").
After a few false starts, you will finally reach a completely collapsed state in which each chair is assigned to exactly one person and all the rules are followed. Done!
From wedding to bitmaps
This is not a theoretical example. You really can implement the option of collapse of the wave function, which will create a seating plan for guests for the wedding. However, in the more traditional Wavefunction Collapse, we usually try not to seat people at the wedding, but to arrange the pixels in the output image. However, the process will be very similar. We teach the algorithm a set of rules that the output should satisfy. We initialize the wave function. We perform the collapse of one element and extend the consequences to the rest of the wave function. And we continue to do so, either until the wave function completely collapses, or until we reach a contradiction.
The traditional collapse of the wave function differs from the wedding collapse in the way we teach the algorithm the rules that it must follow. In the wedding version, we had to write down the rules ourselves. But in the traditional version, we just give the algorithm an example image, and based on it, the algorithm creates the rest. He parses an example, analyzes its patterns and finds out how pixels or tiles should line up.
Let's start researching the real collapse of a wave function by looking at a simple special case, which
ExUtumno (the creator of the algorithm) calls the Simple Tiled Model .Simple tiled model
In the Simple Tiled Model, input and output images are constructed from a small number of predefined tiles, and each square in the output image is limited to only its four nearest neighbors. For example, suppose we generate random worlds for a two-dimensional game with a top view. We can have tiles for land, coast and sea, as well as a set of rules such as “the coast can be near the sea”, “land can be near the coast” and “the sea can be near another sea”.

The Simple Tiled Model takes into account the symmetry and rotation of its tiles. For example, land may be near the coast, but only in the correct orientation.

This symmetry processing provides better output images, but complicates the code. To keep things simple, let's look at an even simpler form of wave function collapse, which I called Even Simpler Tiled Model .
Even Simpler Tiled Model
Even the Simpler Tiled Model (“an even simpler tile model”) is similar to the Simple Tiled Model, but its tiles do not have symmetry properties. Each tile is one pixel of the same color, that is, we will not be able to confuse their edges in any way.

Even Simpler Tiled Model rules determine which tiles can be placed next to each other and in which orientation. Each rule is a tuple of three elements (3-tuple): two tiles and a direction. For example,
(SEA, COAST, LEFT) means that the SEA tile (sea) can be COAST tile (coast). This rule must be accompanied by another rule that describes the situation from the point of view of COAST - (COAST, SEA, RIGHT) .
If you want the
SEA tiles to be located not only to the COAST tiles. then they need additional rules: (SEA, COAST, RIGHT) and (COAST, SEA, LEFT) .As I said above, we do not need to create a list of all these rules ourselves. The collapse of the wave function can create a set of rules for Even Simpler Tile Model by parsing an example image and collecting a list of all 3-tuple it contains.

Having examined the example image shown above, Even Simpler Tiled Model notices that the sea tiles can only be under or to the side of the coast tiles, or anywhere near other sea tiles. She also notes that coast tiles can be located next to land, sea, or other coast tiles, but only above sea tiles and under land tiles. She does not try to derive any more complex rules, for example, "sea tiles should be near at least one sea tile" or "each island must contain at least one land tile." None of the tiles can affect the fact that some types of tiles can or cannot be located two or more squares from them. This is similar to a wedding plan model, with the only rule: “X can sit next to Y”.
When analyzing the incoming image, we also need to record the frequency with which each of the tiles meets. Later, we use these numbers as weights when choosing the wave function of the square whose collapse needs to be performed, as well as when choosing the tile assigned to the square when it is collapsed.
Having learned the rules that the output image must adhere to, we are ready to build the collapse of the wave function of the output image.
Collapse
As in the wedding example, we begin the process of collapsing with a wave function in which each square of the output image is in a superposition of each type of tile.

We begin by choosing a square whose wave function will collapse. In the wedding example, this choice was made by chance. However, as
ExUtumno noted, people usually approach these tasks differently. Instead, they look for squares with the lowest entropy . Entropy is a measure of uncertainty and disorder. In general, a square with high entropy is a square with many possible tiles remaining in its wave function. It is still not clear to which tile he ultimately collapses. A low entropy square is a square with the fewest possible tiles in the wave function. The set of tiles, to one of which he collapses as a result, is already very limited.For example, in the Even Simpler Tile Model, a square without information about the surrounding squares is unlimited and can become any tile. Therefore, it has a very high entropy. But a square around which several squares have already collapsed can have a choice of only 2 tiles.

The wave function of the central square in the figure above did not completely collapse, but we already know that it cannot be a land tile. However, it is already limited, which means it has an entropy lower than that of the upper right square, which can still be land, sea or coast.
It is such limited tiles with low entropy that people usually pay attention to when they manually solve such problems. Even if you do not use the collapse of the wave function to create a plan for accommodating guests at the wedding and will draw it up yourself, you will still focus on those areas of the plan that already have the greatest number of restrictions. You will not put Dwayne at table 1, and then randomly jump to get Katie at table 7 (which is empty so far). You first put Dwayne, then you will figure out who can sit next to him, then who can sit next to this person, and so on. I have not yet seen the rationale for this, but my intuition says that using this heuristic of minimal entropy is likely to produce less contradictions than if you randomly select squares for collapse.
The Shannon formula is used as the entropy formula in the wave function collapse algorithm. It uses the weights of the tiles that we parsed from the incoming image in the previous step:
# Sums are over the weights of each remaining # allowed tile type for the square whose # entropy we are calculating. shannon_entropy_for_square = log(sum(weight)) - (sum(weight * log(weight)) / sum(weight)) Having calculated the square of the wave function with the smallest entropy, we collapse its wave function. We do this by randomly selecting one of the tiles that are still available for the square, weighted by the weights of the tiles that we parsed from the incoming image. Weights are used because it provides a more realistic output image. Suppose the wave function of a square reports that it can be land or coast. We do not always have to choose one of the options with a probability of 50%. If the input image has more land tiles than the coast, then we should reflect this advantage in the output image. This is realized using simple global weights. If in the example image there are
20 land tiles and 10 coast tiles, then the square collapses into land with a probability of 2/3 , and in the coast - with the remaining probability of 1/3 .Then we extend the consequences of the choice to the rest of the wave function of the output (“if that tile turned out to be the sea, then this tile cannot be land, that is, this cannot be the coast”). When all these tremors have settled, we repeat the process using the minimum entropy heuristic to select the next collapsing tile. We repeat this collapse-propagation cycle, either until the entire wave function of the output image completely collapses and we can return the result, or until we reach a contradiction and return an error.
As a result, we created a world (or mistake).
Where to go next
Having dealt with the Even Simpler Tiled Model, you are ready to climb the ladder of power and complexity of the algorithm. Start with the Simple Tiled Model that we mentioned at the beginning of this post, then go on to the full Overlapping Model. In the Overlapping Model, tiles or pixels affect each other from a distance. If you understand such things, then
ExUtumno notices that the Simple Tiled Model is similar to the Markov chain of order-1, and more complex models resemble chains of a larger order.Wavefunction Collapse can even take into account additional restrictions, for example, “this tile must be sea” or “this pixel must be red” or “there can be only one monster in the output”. All this is described by the README of the main project . You can also study the speed optimizations made to the full implementation. It is not necessary to recalculate the entropy of each square in each iteration, and the dissemination of information by the wave function can be done much faster. These aspects become more important as the size of the output images increases.
The collapse of the wave function is a beautiful and powerful tool that is worth mastering. Think about it the next time you plan a wedding or generate a procedural world.
Source: https://habr.com/ru/post/461323/
All Articles