Greedy approach and slot machines. Analysis of the tasks of the ML-track of the programming championship

We continue to publish analyzes of the tasks that were proposed at the recent championship. Next in line are tasks taken from the qualification round for machine learning specialists. This is the third track out of four (backend, frontend, ML, analytics). Participants needed to make a model for correcting typos in texts, propose a strategy for playing on slot machines, bring to mind a system of recommendations for content, and compose several more programs.

A. Typos

Condition

(epigraph) (from one forum)
- Who composed this nonsense?
- Astrophysicists. They are people too.
- You made 10 mistakes in the word “journalists”.
')
Many users make typing errors, some because of hitting keys, some because of their illiteracy. We want to check if the user could really mean some other word than the one he typed.

More formally, suppose that the following error model takes place: the user begins with a word that he wants to write, and then subsequently makes a number of errors in it. Each mistake is a substitution of some substring of the word for another substring. One error corresponds to replacing only in one position (that is, if the user wants to make a single error by the rule “abc” → “cba”, then from the line “abcabc” he can get either “cbaabc” or “abccba”). After each error, the process repeats. The same rule could be used several times in different steps (for example, in the above example, “cbacba” could be obtained in two steps).

It is required to determine the minimum number of errors a user could make if he had in mind one given word and wrote another.

Decision

Let's try to generate from the correct spelling all possible words with no more than 4 errors. In the worst case, there may be O ((L﹒N) ⁴ ). In the limitations of the problem, this is a rather large number, so you need to figure out how to reduce complexity. Instead, you can use the meet-in-the-middle algorithm: generate words with no more than 2 errors, as well as words from which you can get a user-written word with no more than 2 errors. Note that the size of each of these sets will not exceed 10 ⁶ . If the number of errors made by the user does not exceed 4, then these sets will intersect. Similarly, we can verify that the number of errors does not exceed 3, 2, and 1.

 struct FromTo { std::string from; std::string to; }; std::pair<size_t, std::string> applyRule(const std::string& word, const FromTo &fromTo, int pos) { while(true) { int from = word.find(fromTo.from, pos); if (from == std::string::npos) { return {std::string::npos, {}}; } int to = from + fromTo.from.size(); auto cpy = word; for (int i = from; i < to; i++) { cpy[i] = fromTo.to[i - from]; } return {from, std::move(cpy)}; } } void inverseRules(std::vector<FromTo> &rules) { for (auto& rule: rules) { std::swap(rule.from, rule.to); } } int solve(std::string& wordOrig, std::string& wordMissprinted, std::vector<FromTo>& replaces) { std::unordered_map<std::string, int> mapping; std::unordered_map<int, std::string> mappingInverse; mapping.emplace(wordOrig, 0); mappingInverse.emplace(0, wordOrig); mapping.emplace(wordMissprinted, 1); mappingInverse.emplace(1, wordMissprinted); std::unordered_map<int, std::unordered_set<int>> edges; auto buildGraph = [&edges, &mapping, &mappingInverse](int startId, const std::vector<FromTo>& replaces, bool dir) { std::unordered_set<int> mappingLayer0; mappingLayer0 = {startId}; for (int i = 0; i < 2; i++) { std::unordered_set<int> mappingLayer1; for (const auto& v: mappingLayer0) { auto& word = mappingInverse.at(v); for (auto& fromTo: replaces) { size_t from = 0; while (true) { auto [tmp, wordCpy] = applyRule(word, fromTo, from); if (tmp == std::string::npos) { break; } from = tmp + 1; { int w = mapping.size(); mapping.emplace(wordCpy, w); w = mapping.at(wordCpy); mappingInverse.emplace(w, std::move(wordCpy)); if (dir) { edges[v].emplace(w); } else { edges[w].emplace(v); } mappingLayer1.emplace(w); } } } } mappingLayer0 = std::move(mappingLayer1); } }; buildGraph(0, replaces, true); inverseRules(replaces); buildGraph(1, replaces, false); { std::queue<std::pair<int, int>> q; q.emplace(0, 0); std::vector<bool> mask(mapping.size(), false); int level{0}; while (q.size()) { auto [w, level] = q.front(); q.pop(); if (mask[w]) { continue; } mask[w] = true; if (mappingInverse.at(w) == wordMissprinted) { return level; } for (auto& v: edges[w]) { q.emplace(v, level + 1); } } } return -1; } 

B. Many-armed bandit

Condition

This is an interactive task.

You yourself do not know how it happened, but you found yourself in a hall with slot machines with a whole bag of tokens. Unfortunately, at the box office, they refuse to accept tokens back, and you decided to try your luck. There are many slot machines in the hall that you can play. For one game with a slot machine you use one token. In case of a win, the machine gives you one dollar, in case of a loss - nothing. Each machine has a fixed probability of winning (which you do not know), but it is different for different machines. Having studied the website of the manufacturer of these machines, you found out that the probability of winning for each machine is randomly selected at the manufacturing stage from a beta distribution with certain parameters.

You want to maximize your expected winnings.

Decision

This problem is well known, it could be solved in different ways. The main decision of the jury implemented the Thompson sampling strategy, but since the number of steps was known at the beginning of the program, there are more optimal strategies (for example, UCB1). Moreover, one could even get by with the epsilon-greedy-strategy: with a certain probability ε play a random machine and with a probability (1 - ε) play a machine with the best victory statistics.

 class SolverFromStdIn(object): def __init__(self): self.regrets = [0.] self.total_win = [0.] self.moves = [] class ThompsonSampling(SolverFromStdIn): def __init__(self, bandits_total, init_a=1, init_b=1): """ init_a (int): initial value of a in Beta(a, b). init_b (int): initial value of b in Beta(a, b). """ SolverFromStdIn.__init__(self) self.n = bandits_total self.alpha = init_a self.beta = init_b self._as = [init_a] * self.n # [random.betavariate(self.alpha, self.beta) for _ in range(self.n)] self._bs = [init_b] * self.n # [random.betavariate(self.alpha, self.beta) for _ in range(self.n)] self.last_move = -1 random.seed(int(time.time())) def move(self): samples = [random.betavariate(self._as[x], self._bs[x]) for x in range(self.n)] self.last_move = max(range(self.n), key=lambda x: samples[x]) self.moves.append(self.last_move) return self.last_move def set_reward(self, reward): i = self.last_move r = reward self._as[i] += r self._bs[i] += (1 - r) return i, r while True: n, m = map(int, sys.stdin.readline().split()) if n == 0 and m == 0: break alpha, beta = map(float, sys.stdin.readline().split()) solver = ThompsonSampling(m) for _ in range(n): print >> sys.stdout, solver.move() + 1 sys.stdout.flush() reward = int(sys.stdin.readline()) solver.set_reward(reward) 

C. Alignment of sentences

Condition

One of the most important tasks for training a good machine translation model is a good case of parallel sentences. Typically, the source for parallel offers is parallel documents. It turns out that often in order to build a certain corpus of parallel sentences, you do not need to know anything but their lengths. In particular, you may notice that the longer the sentence in the source language, the longer it will most likely be translated. Some difficulty lies in the fact that during the translation the number of sentences in the text can change: sometimes two neighboring sentences in the translation can be combined into one, or vice versa - one sentence could be divided into two. In some rare cases, sentences may be omitted entirely in a translation, or a translation may appear in a translation that was not in the original.

More formally, suppose the following generative model for parallel enclosures is true. At each step, we do one of the following:

1. Stop

With probability p _h, hull generation ends.

2. [1-0] Skipping offers

With probability p _{d we} ascribe one sentence to the original text. We do not attribute anything to the translation. The length of the sentence in the original language L ≥ 1 is selected from the discrete distribution:

.

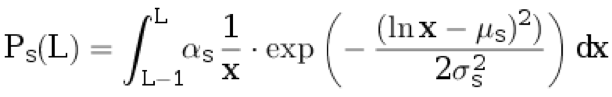Here μ _s , σ _s are the distribution parameters, and α _s is the normalization coefficient chosen so that .

3. [0-1] Insert proposal

With probability p _{i we} ascribe one sentence to the translation. We do not ascribe anything to the original. The length of a sentence in a translation language L ≥ 1 is selected from a discrete distribution:

.

Here μ _t , σ _t are the distribution parameters, and α _t is the normalization coefficient chosen so that .

4. Translation

With probability (1 - p _d - p _i - p _h ) we take the length of the sentence in the original language L _s ≥ 1 from the distribution p _s (with rounding up). Next, we generate the length of the sentence in the translation language L _t ≥ 1 from the conditional discrete distribution:

.

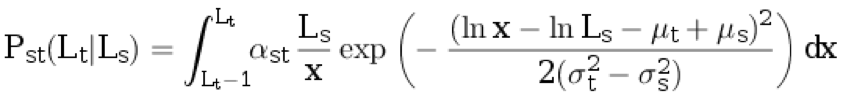Here, α _st is the normalization coefficient, and the remaining parameters are described in the previous paragraphs.

Next is another step:

1. [2-1] With probability p _{split s, the} generated sentence in the original language splits into two non-empty sentences, so that the total number of words increases by exactly one . The probability that a sentence of length L _{s will} fall apart into parts of length L ₁ and L ₂ (that is, L ₁ + L ₂ = L _s + 1) is proportional to P _s (L ₁ ) ⋅ P _s (L ₂ ).

2. [1-2] With probability p _{split t, the} generated sentence in the target language splits into two non-empty sentences, so that the total number of words increases by exactly one. The probability that a sentence of length L _{t will} fall apart into parts of length L1 and L2 (that is, L ₁ + L ₂ = L _t + 1) is proportional to P _t (L ₁ ) ⋅ P _t (L ₂ ).

3. 3. [1-1] With the probability (1 - p _{split s} - p _{split t} ), none of the pair of generated sentences will decay.

Decision

The task is a special case of alignment using hidden Markov models (HMM alignment). The main idea is that you can calculate the probability of generating a specific pair of documents using this model and the forward algorithm : in this case, the state is a pair of document prefixes. Accordingly, the required probability of alignment of a specific pair of parallel sentences can be calculated by the forward-backward algorithm.

D. Guideline

Condition

Consider a feed of recommendations for heterogeneous content. It mixes objects of various types (pictures, videos, news, etc.). These objects are usually ordered by relevance to the user: the more relevant (interesting) the object to the user, the closer to the top of the list of recommendations. However, with such ordering, situations often arise in which several objects of the same type appear in the list of recommendations. This greatly affects the external variety of our recommendations and therefore users do not like it. It is necessary to implement an algorithm that, according to the list of recommendations, will compose a new list that will be free from this problem and will be most relevant.

Let an initial list of recommendations be given a = [a ₀ , a ₁ , ..., a _{n - 1} ] of length n> 0. An object with number i has type with number b _i ∈ {0, ..., m - 1}. In addition, an object under number i has relevance r (a _i ) = 2 _−i . Consider the list that is obtained from the initial one by selecting a subset of objects and rearranging them: x = [a _{i 0} , a _{i 1} , ..., a _{i k − 1} ] of length k (0 ≤ k ≤ n). A list is called admissible if no two consecutive objects in it match in type, i.e., b _{i j} ≠ b _{i j + 1} for all j = 0, ..., k − 2. The relevance of the list is calculated by the formula $$$\ sum_ {j = 0} ^ {k-1} 2 _ {- j} r (a_ {i_j})$. You need to find the maximum relevance list among all valid.

Decision

Using simple mathematical calculations, it can be shown that the problem can be solved by a “greedy” approach, that is, in the optimal list of recommendations, each position has the most relevant object of all that are valid at the same beginning of the list. The implementation of this approach is simple: we take objects in a row and add them to the answer, if possible. When an invalid object is encountered (the type of which coincides with the type of the previous one), we put it aside in a separate queue, from which we insert it into the response as soon as possible. Note that at every moment in time, all objects in this queue will have a matching type. At the end, several objects may remain in the queue, they will no longer be included in the response.

  std::vector<int> blend(int n, int m, const std::vector<int>& types) { std::vector<int> result; std::queue<int> repeated; for (int i = 0; i < n; ++i) { if (result.empty() || types[result.back()] != types[i]) { result.push_back(i); if (!repeated.empty() && types[repeated.front()] != types[result.back()]) { result.push_back(repeated.front()); repeated.pop(); } } else { repeated.push(i); } } return result; } 

D. Clustering character sequences

There is a finite alphabet A = {a ₁ , a ₂ , ..., a _{K − 1} , a _K = S}, a _i ∈ {a, b, ..., z}, S is the end of the line.

Consider the following method of generating random strings over the alphabet A:

1. The first character x ₁ is a random variable with the distribution P (x ₁ = a _i ) = q _i (it is known that q _K = 0).
2. Each next character is generated on the basis of the previous one in accordance with the conditional distribution P (x _i = a _j || x _{i - 1} = a _l ) = p _jl .
3. If x _i = S, generation stops and the result is x ₁ x ₂ ... x _{i − 1} .

A set of lines generated from a mixture of two described models with different parameters is given. It is necessary for each row to give the index of the chain from which it was generated.

Decision

The problem is solved using the EM algorithm : it is assumed that the presented sample is generated from a mixture of two Markov chains whose parameters are restored during iterations. A restriction of 80% of the correct answers is made so that the correctness of the solution is not affected by examples that have a high probability in both chains. These examples, therefore, if properly restored, can be assigned to a chain that is incorrect in terms of the generated response.

 import random import math EPS = 1e-9 def empty_row(size): return [0] * size def empty_matrix(rows, cols): return [empty_row(cols) for _ in range(rows)] def normalized_row(row): row_sum = sum(row) + EPS return [x / row_sum for x in row] def normalized_matrix(mtx): return [normalized_row(r) for r in mtx] def restore_params(alphabet, string_samples): n_tokens = len(alphabet) n_samples = len(string_samples) samples = [tuple([alphabet.index(token) for token in s] + [n_tokens - 1, n_tokens - 1]) for s in string_samples] probs = [random.random() for _ in range(n_samples)] for _ in range(200): old_probs = [x for x in probs] # probs fixed p0, A = empty_row(n_tokens), empty_matrix(n_tokens, n_tokens) q0, B = empty_row(n_tokens), empty_matrix(n_tokens, n_tokens) for prob, sample in zip(probs, samples): p0[sample[0]] += prob q0[sample[0]] += 1 - prob for t1, t2 in zip(sample[:-1], sample[1:]): A[t1][t2] += prob B[t1][t2] += 1 - prob A, p0 = normalized_matrix(A), normalized_row(p0) B, q0 = normalized_matrix(B), normalized_row(q0) trans_log_diff = [ [math.log(b + EPS) - math.log(a + EPS) for b, a in zip(B_r, A_r)] for B_r, A_r in zip(B, A) ] # A, p0, B, q0 fixed probs = empty_row(n_samples) for i, sample in enumerate(samples): value = math.log(q0[sample[0]] + EPS) - math.log(p0[sample[0]] + EPS) for t1, t2 in zip(sample[:-1], sample[1:]): value += trans_log_diff[t1][t2] probs[i] = 1.0 / (1.0 + math.exp(value)) if max(abs(x - y) for x, y in zip(probs, old_probs)) < 1e-9: break return [int(x > 0.5) for x in probs] def main(): N, K = list(map(int, input().split())) string_samples = [] alphabet = list(input().strip()) + [''] for _ in range(N): string_samples.append(input().rstrip()) result = restore_params(alphabet, string_samples) for r in result: print(r) if __name__ == '__main__': main() 

---

Here are the breakdowns of tasks on the backend and frontend .