The book “Perfect Algorithm. Graph Algorithms and Data Structures "

Hello, habrozhiteli! Algorithms are the heart and soul of computer science. You can’t do without them, they are everywhere - from network routing and genomics calculations to cryptography and machine learning. The “Perfect Algorithm” will turn you into a real pro who will set tasks and masterfully solve them both in life and at an interview when hiring any IT company.

In the second book, Tim Rafgarden, an algorithm guru, talks about graph search and its application, the shortest path search algorithm, and the use and implementation of some data structures: heaps, search trees, hash tables, and the Bloom filter.

This post presents an excerpt from Bloom Filters: The Basics.

What is this book about

The second part of the book “The Perfect Algorithm” is an introductory course on the basics of literacy on the following three topics.
')
Graph search and applications . Graphs model a number of different types of networks, including road, communication, social networks and networks of dependencies between tasks. Graphs can be complex, but there are some incredibly fast primitives to talk about graph structure. We'll start with linear-time graph search algorithms, from applications ranging from network analysis to building a sequence of operations.

The shortest paths . In the shortest path problem, the goal is to calculate the best route in the network from point A to point B. This task has obvious applications, such as calculating traffic routes, and also occurs in disguised form in many other universal tasks. We will generalize one of our graph search algorithms and come to the famous Dijkstra shortest path search algorithm.

Data structures . This book will make you a highly educated user of several different data structures designed to support an evolving set of objects with their associated keys. The main goal is to develop an intuition about which data structure is right for your application. Additional sections provide guidelines for implementing these data structures from scratch.

First, we discuss heaps that can quickly identify a stored object with the smallest key, and are also useful for sorting, implementing a priority queue, and implementing Dijkstra's almost linear-temporal algorithm. Search trees maintain the complete ordering of keys on stored objects and support an even wider range of operations. Hash tables are optimized for ultrafast search operations and are widespread in modern programs. We also look at the Bloom filter, a close relative of the hash table, which uses less space due to random errors.

You can familiarize yourself with the contents of the book in more detail in the “Conclusions” sections, which complete each chapter and identify the most important points. Sections of the book, marked with an asterisk, are the most advanced in terms of the level of information presented. If the book is designed for a superficial familiarization with the topic, then the reader can skip them without losing the integrity of the written.

Topics covered in three other parts . The first part of the book “Perfect Algorithm. Fundamentals ”covers asymptotic notations (the O-large and its close relatives notation),“ divide and conquer ”algorithms and the main recurrence relation theorem — the main method, randomized quick sorting and its analysis, and linear-temporal selection algorithms. The third part deals with greedy algorithms (planning, minimal spanning trees, clustering, Huffman codes) and dynamic programming (backpack problem, sequence alignment, shortest paths, optimal search trees). The fourth part is devoted to NP-completeness, what it means for an algorithm designer, and strategies for solving computationally insoluble problems, including heuristic analysis and local search.

12.5. Bloom Filters: The Basics

Bloom filters are close relatives of hash tables. They are very compact, but instead periodically make mistakes. This section describes how Bloom filters are good and how they are implemented, while section 12.6 sets out a compromise curve between the amount of space used by the filter and its error rate.

12.5.1. Supported Operations

The reason for the existence of Bloom filters is essentially the same as that of a hash table: superfast insert and view operations, thanks to which you can quickly remember what you saw and what didn’t. Why should we be bothered by a different data structure with the same set of operations? Because Bloom filters are preferable to hash tables in applications in which space is worth its weight in gold, and a random error is not an obstacle to the transaction.

Like hash tables with open addressing, Bloom filters are much easier to implement and imagine in the mind when they support only the Insert and View operations (and without the Delete operation). We will focus on this case.

BLOOM FILTERS: SUPPORTED OPERATIONS

View: with the key k, return “yes” if k was previously inserted into the Bloom filter, and “no” otherwise.
Paste: add a new key k to the Bloom filter.

Bloom filters are very spatially efficient; typically they may require only 8 bits per insert. This is quite unbelievable, since 8 bits is completely insufficient to remember even a 32-bit key or pointer to an object! For this reason, the View operation in the Bloom filter returns only the answer “yes” / “no”, whereas in the hash table, this operation returns a pointer to the desired object (if it is found). That is why the Insert operation now accepts only the key, and not the (pointer to) object.

Unlike all other data structures that we studied, Bloom filters can be wrong. There are two types of errors: false negatives when the View operation returns “false” even if the requested key has already been inserted previously, and false statements (or triggers) when the View operation returns “true”, although the requested key has not yet been inserted in the past . In section 12.5.3 we will see that the basic Bloom filters never suffer from false negatives, but they can have “phantom elements” in the form of false statements. Section 12.6 shows that the frequency of false claims can be controlled by adjusting the use of space accordingly. A typical implementation of a Bloom filter may have an error rate of about 1% or 0.1%.

The execution times for the Insert and View operations are as fast as in the hash table. And even better, these operations are guaranteed to be performed in constant time, regardless of the implementation of the Bloom filter and data set1. However, the implementation and data set affect the filter error rate.

To summarize the advantages and disadvantages of Bloom filters over hash tables:

BLOOM FILTER AGAINST HASH TABLES

1. Pros: more spatially effective.

2. Pros: guaranteed permanent-time operations for each data set.

3. Cons: cannot store pointers to objects.

4. Cons: more complex deletions compared to a hash table with a clutch.

5. Cons: non-zero probability of a false statement.

The list of indicators for the basic Bloom filters is as follows.

Table 12.4. Basic Bloom filters: supported operations and their execution time. The dagger sign (†) indicates that the View operation has a controllable but nonzero probability of false statements


Bloom filters should be used instead of hash tables in applications in which their advantages matter and their disadvantages are not an obstacle to the transaction.

WHEN TO USE THE BLOOM FILTER

If an application requires a quick search with a dynamically evolving set of objects, space is worth its weight in gold and an acceptable small number of false claims, then the Bloom filter is usually the preferred data structure.

12.5.2. Applications

Next, there are three uses with repeated scans, where saving space can be important, and false statements are not an obstacle to the transaction.

Spellcheckers. Back in the 1970s, Bloom filters were used to implement spell checkers - spellcheckers. At the pre-processing stage, each word in the dictionary is inserted into the Bloom filter. Spelling of a document comes down to one operation. Look at a word in a document, marking any words for which this operation returns "no."

In this appendix, a false statement corresponds to an invalid word that the spellchecker inadvertently accepts. Such mistakes did not make spellcheckers ideal. However, in the early 1970s, space was worth its weight in gold, so using Bloom filters at that time was a win-win strategy.

Prohibited passwords . An old application that remains valid to this day tracks forbidden passwords - passwords that are too common or too easy to guess. Initially, all forbidden passwords are inserted into the Bloom filter; additional forbidden passwords can be inserted later, as needed. When a user tries to set or reset his password, the system searches for the proposed password in the Bloom filter. If the search returns “yes”, then the user is prompted to try again with a different password. Here, a false statement is translated into a strong password, which the system rejects.

Provided that the error rate is not too high, say no more than 1% or 0.1%, this does not matter much. From time to time, some users will need one additional attempt to find a password acceptable to the system.

Internet routers . A number of today's mind-blowing applications of Bloom filters take place deep in the Internet, where data packets go through streaming routers. There are many reasons why a router might want to quickly recall what it saw in the past. For example, the router may want to find the source IP address of the packet in the list of blocked IP addresses, track the contents of the cache in order to avoid spurious cache views, or keep statistics that help identify a denial of service network attack. The packet arrival rate requires superfast views, and the limited memory of the router makes space worth its weight in gold. These applications are directly managed by the Bloom Filter.

12.5.3. Implementation

Looking inside the Bloom filter, you can see an elegant implementation. The data structure supports an n-bit string or, equally, an array A of length n in which each element is 0 or 1. (All elements are initialized to zero.) This structure also uses m hash functions h1, h2, ..., hm , each mapping the universe U of all possible keys to the set {0, 1, 2, ..., n - 1} of positions in the array. The parameter m is proportional to the number of bits used by the Bloom filter for insertion, and, as a rule, is a small constant (for example, 5).

Whenever a key is inserted into a Bloom filter, each of the m hash functions sets a flag, setting the corresponding bit of array A to 1.

BLOOM FILTER: INSERT (ON KEY)

for i = 1 to m do A[hi(k)] := 1 

For example, if m = 3 and h1 (k) = 23, h2 (k) = 17 and h3 (k) = 5, inserting k causes the 5th, 17th and 23rd bits of the array to be set equal 1 (Fig. 12.5).


In the View operation, the Bloom filter searches for the fingerprint that might remain after insert k.

BLOOM FILTER: VIEW (KEY KEY)

 for i = 1 to m do if A [hi (k)] = 0 then return «» return «» 

Now we can see why Bloom filters cannot suffer from false negatives. When the key k is inserted, the corresponding m bits are set to 1. During the lifetime of the Bloom filter, the bits can change their value from 0 to 1, but not vice versa. Thus, these m bits remain 1 forever. Each subsequent View k operation is guaranteed to return the correct yes answer.

We can also see how false statements arise. Suppose that m = 3 and the four keys k1, k2, k3, k4 have the following hash values:


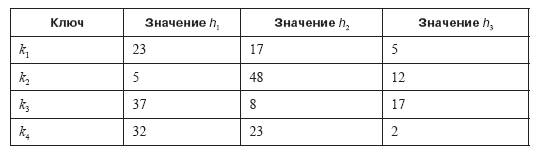
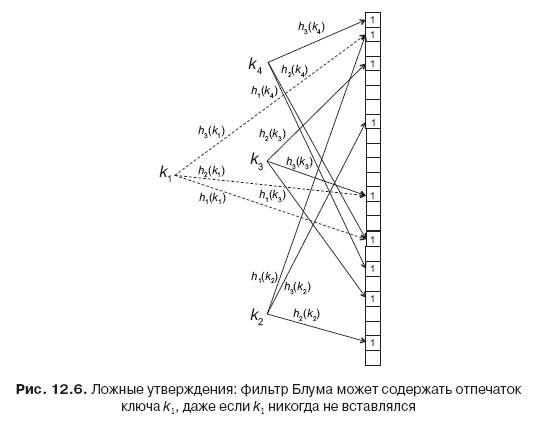
Suppose we insert k1, k2, k3 and k4 into a Bloom filter (Figure 12.6). These three inserts lead to a total of nine bits being set equal to 1, including three bits in the fingerprint of key k1 (5, 17 and 23). At this point, the Bloom filter can no longer distinguish whether or not key k1 has been inserted. Even if k1 was not inserted into the filter, the search will return “yes”, which is a false statement.

Intuitively, we can assume that with an increase in the size n of the Bloom filter, the number of overlays between the fingerprints of different keys should decrease, which, in turn, leads to a smaller number of false statements. But the primary goal of the Bloom filter is to save space. Is there a middle ground where both n and the frequency of false statements are simultaneously small? The answer is not obvious and requires some mathematical analysis undertaken in the next section.



»More details on the book can be found on the publisher’s website
» Contents
» Excerpt

For Khabrozhiteley 20% discount on the coupon - Algorithms
Upon payment of the paper version of the book, an electronic book is sent by e-mail.