Lecture course "Basics of digital signal processing"
Hello!
I am often approached by people with questions on problems in the field of digital signal processing (DSP). I tell in detail the nuances, suggest the necessary sources of information. But, as time has shown, all listeners lack practical tasks and examples in the process of learning this area. In this regard, I decided to write a short online course on digital signal processing and put it in open access .
Most of the training material for visual and interactive presentation is implemented using Jupyter Notebook . It is assumed that the reader has a basic knowledge of higher mathematics, and also knows a little programming language Python.
')

This course contains materials in the form of complete lectures on various topics in the field of digital signal processing. Materials are presented using Python libraries (numpy, scipy, matplotlib, etc.). The main information for this course is taken from my lectures, which I, as a graduate student, read to students of the Moscow Energy Institute (NIU MEI). Part of the information from these lectures was used at training seminars at the Center for Modern Electronics , where I acted as a lecturer. In addition, this material includes the translation of various scientific articles, compilation of information from reliable sources and literature on the subject of digital signal processing, as well as official documentation on the application packages and built-in functions of the scipy and numpy libraries of the Python language.
For users of MATLAB (GNU Octave), mastering the material in terms of program code is not difficult, since the main functions and their attributes are largely identical and similar to the methods from the Python libraries.
All materials are grouped by the main topics of digital signal processing:
The list of lectures is sufficientbut, of course, incomplete for an introductory acquaintance with the area of DSP. With free time, I plan to support and develop this project.
All materials are absolutely free and available as an open repository on my githaba as an opensource project . The materials are presented in two formats - in the form of notebooks Jupyter Notebook for interactive work, study and editing, and in the form of HTML files compiled from these notebooks (after downloading from the github they have quite a suitable format for reading and printing).
Below is a very brief description of the course sections with some explanations, terms and definitions. Basic information is available in the original lectures, here is only a brief overview!
The introductory section, which contains basic information on the types of signals. The concept of a discrete sequence, delta functions and Heaviside functions (a single jump) is introduced.
All signals according to the method of representation on the set can be divided into four groups:
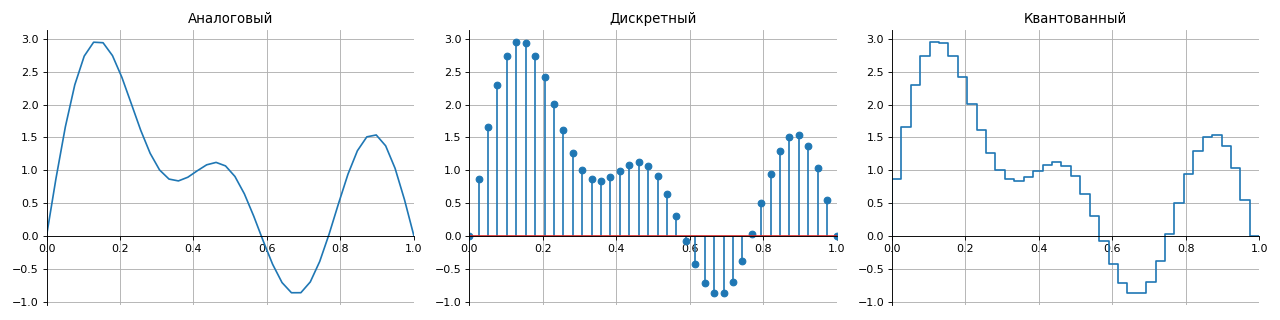
To correctly restore an analog signal from digital without distortion and loss, a sampling theorem known as the Kotelnikov (Nyquist-Shannon) theorem is used.
Such an interpretation is valid provided that the continuous function of time occupies a frequency band from 0 to the value of the upper frequency. If the quantization and sampling steps are chosen incorrectly, the conversion of the signal from analog to discrete form will occur with distortion.
Also in this section Z-transformation and its properties are described, the representation of discrete sequences in Z-form is shown.
Example of a finite discrete sequence:
An example of the same sequence in Z-form:
X (z) = 2 + z -1 - 2z -2 + 2z -4 + 3z -5 + 1z -6
This section describes the concept of the time and frequency domain of a signal. The definition of the discrete Fourier transform (DFT) is introduced. Considered direct and inverse DFT, their main properties. The transition from the DFT to the fast Fourier transform (FFT) algorithm at base 2 (frequency and time decimation algorithms) is shown. Reflects the effectiveness of the FFT in comparison with the DFT.
In particular, this section describes the Python package scipy.ffpack for computing various Fourier transforms (sine, cosine, direct, inverse, multidimensional, real).
Fourier transform allows you to represent any function as a set of harmonic signals! The Fourier transform underlies the convolution methods and the design of digital correlators, is actively used in spectral analysis, and is used when working with long numbers.
Features of the spectra of discrete signals:
1. The spectral density of a discrete signal is a periodic function with a period equal to the sampling frequency.
2. If the discrete sequence is real , then the modulus of the spectral density of such a sequence is an even function, and the argument is an odd function of frequency.
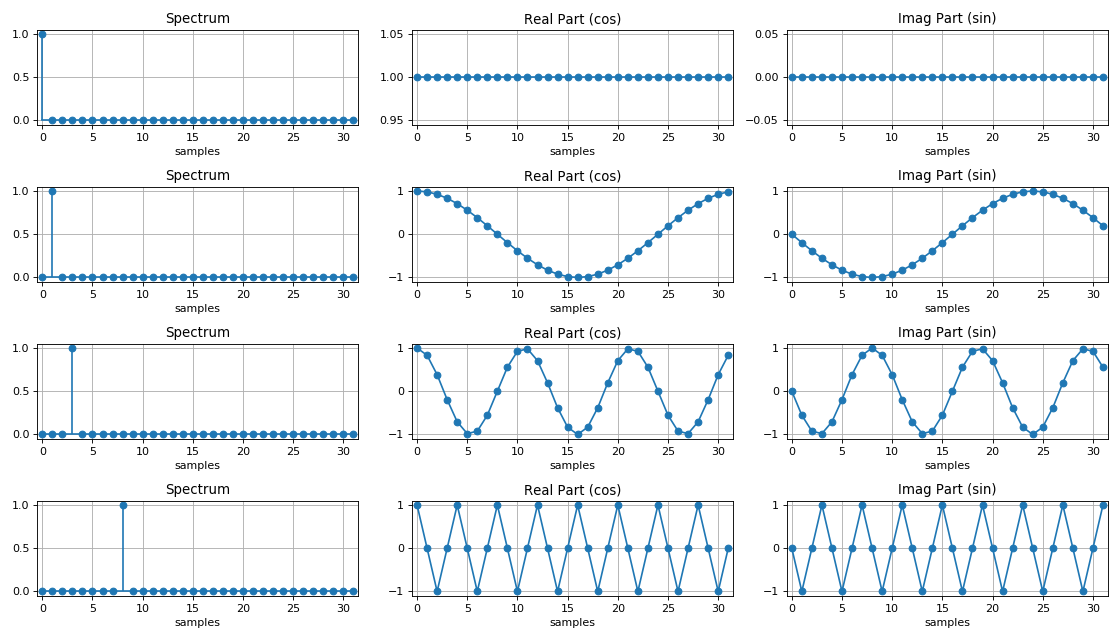
Harmonic spectrum:
The effectiveness of the FFT algorithm and the number of operations performed linearly depends on the length of the sequence N:
As you can see, the longer the conversion, the greater the savings in computing resources (in terms of processing speed or the number of hardware blocks)!
Any arbitrary waveform can be represented as a set of harmonic signals of different frequencies. In other words, a complex waveform in the time domain has a set of complex samples in the frequency domain, which are called * harmonics *. These readings express the amplitude and phase of the harmonic impact at a specific frequency. The larger the set of harmonics in the frequency domain, the more accurate the signal of complex shape.

This section introduces the notion of correlation and convolution for discrete random and deterministic sequences. The connection of the autocorrelation and mutual correlation functions with convolution is shown. The properties of convolution are described, in particular, methods of linear and cyclic convolution of a discrete signal with detailed analysis are considered using the example of a discrete sequence. In addition, a method for calculating “fast” convolution using FFT algorithms is shown.
In real problems, it is often asked about the degree of similarity of one process to another, or about the independence of one process from another. In other words, it is required to determine the relationship between the signals, that is, to find a correlation . Correlation methods are used in a wide range of tasks: signal searching, computer vision and image processing, in radar tasks to determine the characteristics of targets and determine the distance to an object. In addition, using the correlation search for weak signals in the noise.
Convolution describes the interaction of signals with each other. If one of the signals is the impulse response of the filter, then the convolution of the input sequence with the impulse response is nothing like the response of the circuit to an input. In other words, the resulting signal reflects the signal passing through the filter.
Autocorrelation function (ACF) is used in coding information. The choice of the coding sequence according to the parameters of length, frequency and shape is largely due to the correlation properties of this sequence. The best code sequence has the lowest probability of false detection or response (for detecting signals, for threshold devices) or false synchronization (for transmitting and receiving code sequences).
This section presents a table comparing the efficiency of fast convolution and convolution calculated by a direct formula (the number of real multiplications).
As you can see, for FFT lengths up to 64, fast convolution loses from the direct method. However, with an increase in the length of the FFT, the results change in the opposite direction — fast convolution begins to outperform the direct method. Obviously, the greater the length of the FFT, the better the gain of the frequency method.
In this section we introduce the concept of random signals, the density of the probability distribution, the law of distribution of a random variable. Mathematical moments are considered - the mean (expected value) and the variance (or the root of this quantity is the standard deviation). Also in this section we consider the normal distribution and the concept of white noise associated with it, as the main source of noise (interference) in signal processing.
A random signal is a function of time, the values of which are unknown in advance and can be predicted only with a certain probability . The main characteristics of random signals include:
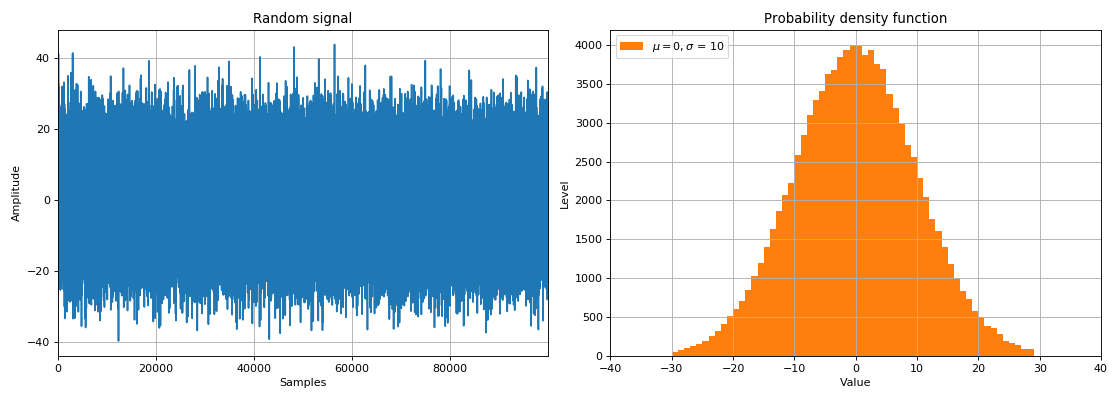
In DSP tasks, random signals are divided into two classes:
Using random variables, it is possible to simulate the effect of a real medium on the passage of a signal from a source to a data receiver. When a signal passes through a noisy link, so-called white noise is added to the signal. As a rule, the spectral density of such noise is uniformly (equally) distributed at all frequencies, and the noise values in the time domain are normally distributed (Gaussian distribution law). Since white noise is physically added to the amplitudes of the signal at selected time samples, it is called additive white Gaussian noise (AWGN).
This section shows the main ways to change one or more parameters of a harmonic signal. The concepts of amplitude, frequency and phase modulation are introduced. In particular, linear frequency modulation applied in radar tasks is highlighted. The main characteristics of the signals, the spectra of the modulated signals depending on the modulation parameters are shown.

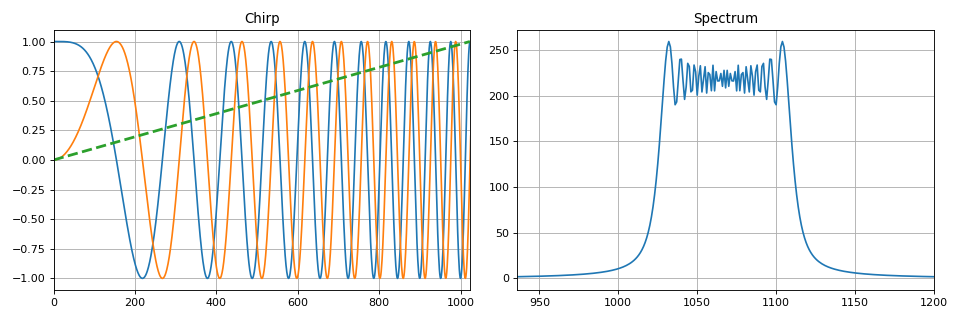
For convenience, Python has created a set of functions that implement the listed types of modulation. An example of the implementation of the chirp signal:
Also in this section from the theory of transmission of discrete messages describes the types of digital modulation - manipulation. As in the case of analog signals, digital harmonic sequences can be manipulated in amplitude, phase and frequency (or in several parameters at once).

A large enough section on digital filtering of discrete sequences. In digital signal processing tasks, data passes through circuits called filters . Digital filters, like analog ones, have different characteristics — frequency response: frequency response, phase response, time response: impulse response, and filter response. Digital filters are used primarily to improve the quality of the signal — to extract a signal from a data sequence, or to degrade unwanted signals — to suppress certain signals in incoming sample sequences.

The section lists the main advantages and disadvantages of digital filters (compared to analog filters). The concept of impulse and transfer filter characteristics is introduced. Two classes of filters are considered - with infinite impulse response (IIR) and finite impulse response (FIR). A method of designing filters in canonical and direct form is shown. For FIR filters, the question of how to transition to a recursive form is considered.
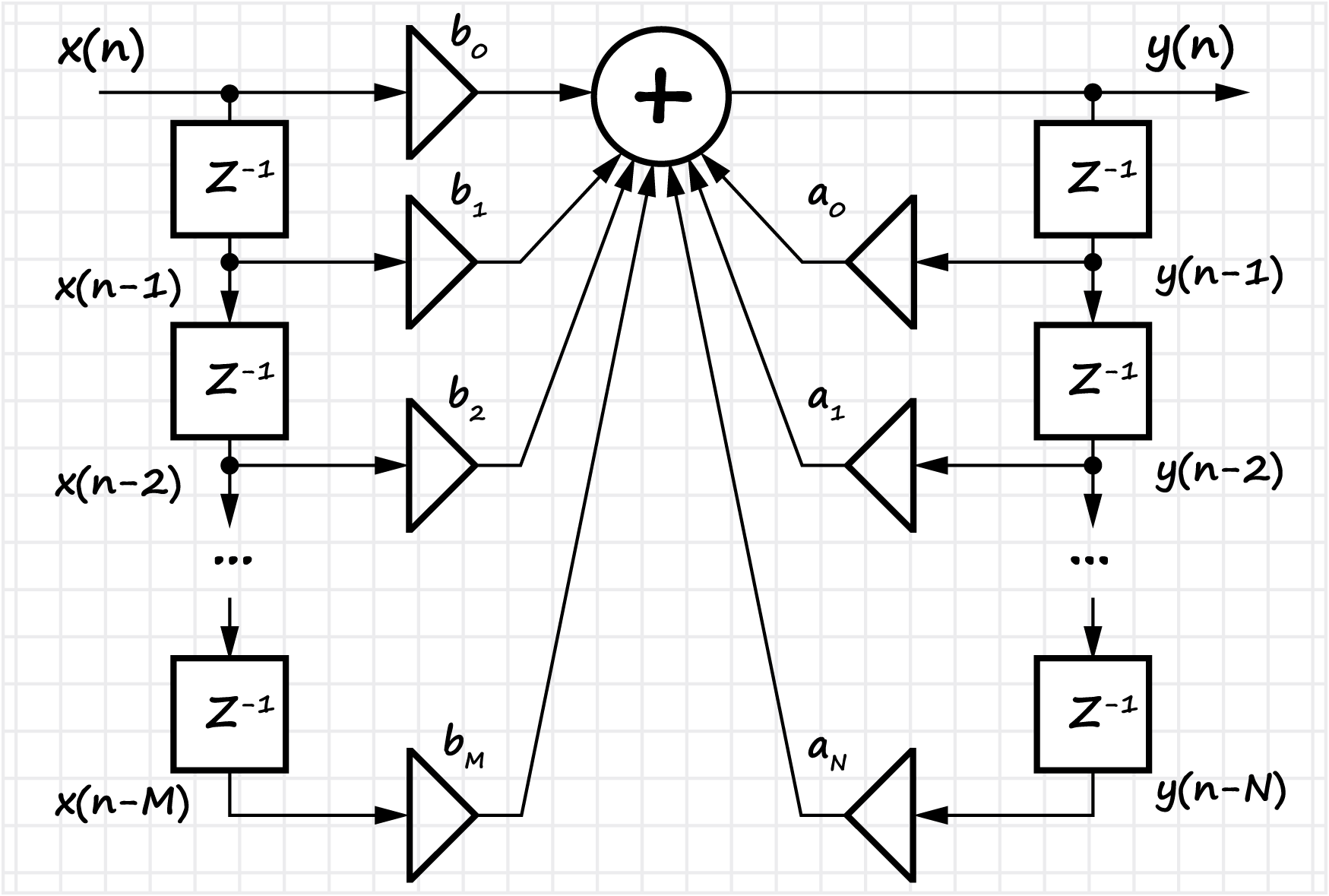
For FIR filters, the filter design process is shown from the development stage of the technical specification (with indication of the main parameters), to the software and hardware implementation - search for filter coefficients (taking into account the form of number representation, data length, etc.). The definitions of symmetric FIR filters, linear phase response and its connection with the concept of group delay are introduced.

In the tasks of digital signal processing, window functions of various forms are used, which, when applied to a signal in the time domain, allow to qualitatively improve its spectral characteristics. A large number of various windows is primarily due to one of the main features of any window overlay. This feature is expressed in the relationship between the level of side lobes and the width of the central lobe. Rule:

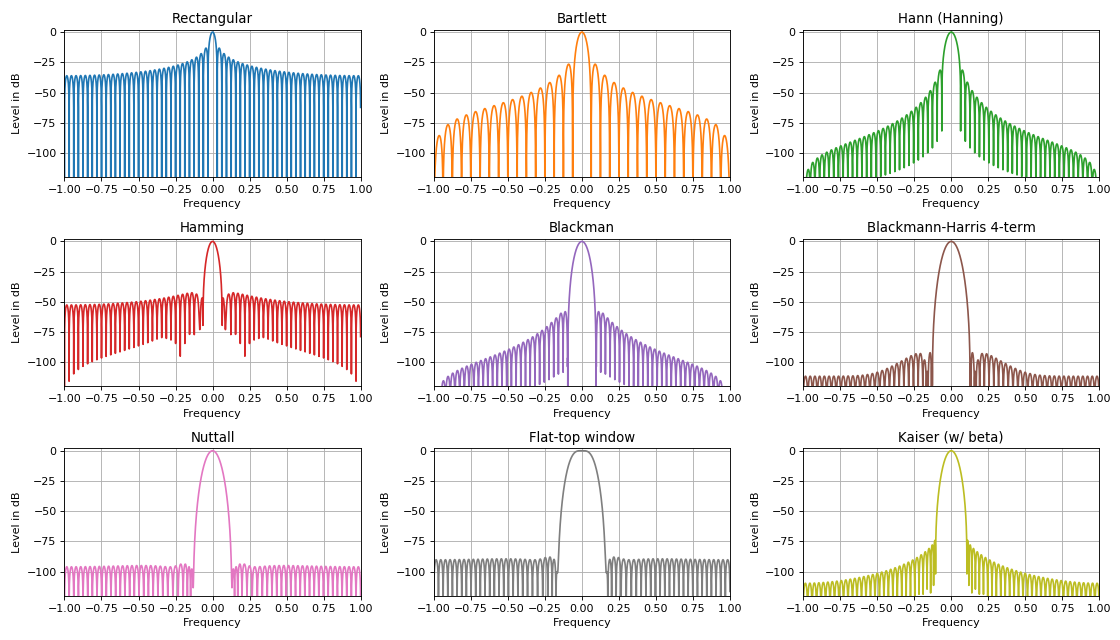
One of the applications of window functions: the detection of weak signals against the background of stronger by suppressing the level of side lobes. The main window functions in DSP tasks are ** triangular, sinusoidal, Lanczos window, Hannah, Hamming, Blackman, Harris, Blackman-Harris, flat top window, Natall, Gauss, Kaiser ** window and many others. Most of them are expressed in a finite series by summing up the harmonic signals with specific weighting factors. Such signals are perfectly implemented in practice on any hardware devices (programmable logic circuits or signal processors).
This section deals with multi-speed signal processing — changes in the sampling rate. Multirate processing of signals (multirate processing) assumes that in the process of linear conversion of digital signals it is possible to change the sampling frequency in the direction of reduction, increase or fractional number of times. This leads to more efficient signal processing, as it opens up the possibility of using the minimum allowable sampling rates and, as a consequence, a significant reduction in the required computing performance of the designed digital system.
Decimation (thinning) - lowering the sampling rate. Interpolation - increasing the sampling rate.
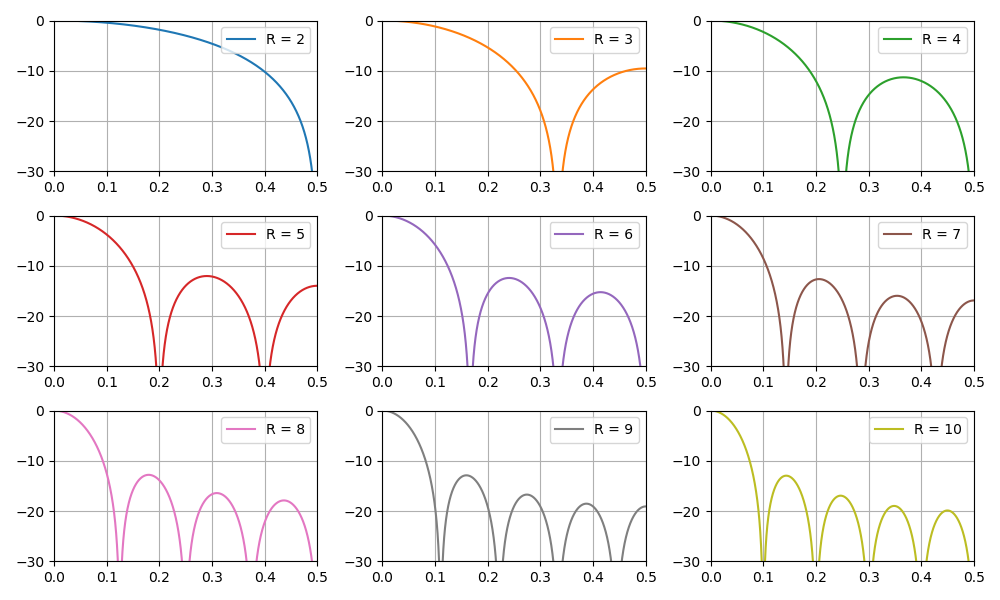
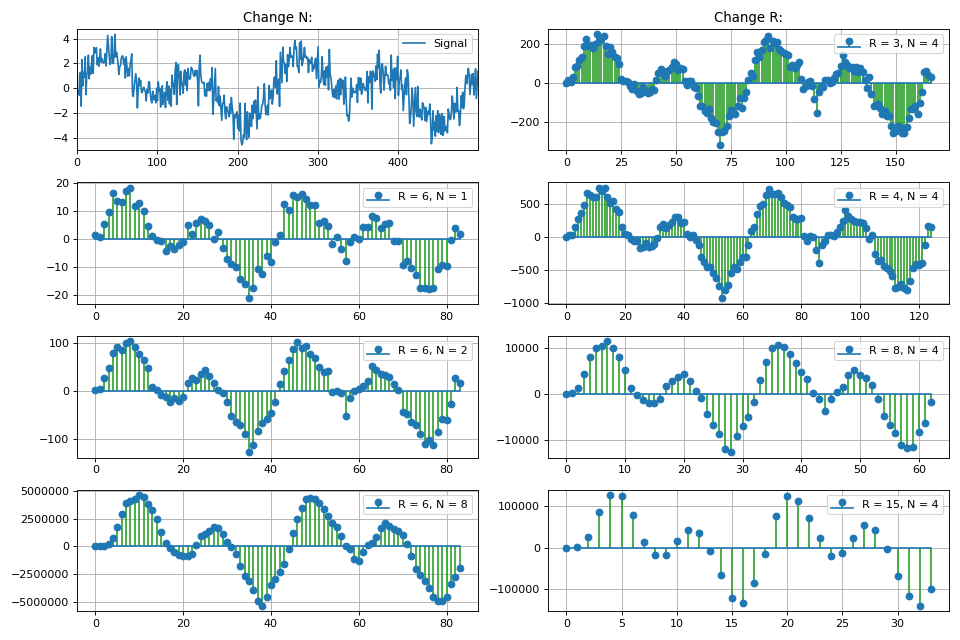
The section also discusses a class of homogeneous FIR filters, which are called integral-comb filters (CIC, Cascaded integrator – comb). The implementation, basic properties and features of CIC filters are shown. Due to the linearity of mathematical operations occurring in the CIC filter, a cascade connection of several filters in a row is possible, which gives a proportional decrease in the side lobe level, but also increases the main lobe of the amplitude-frequency characteristic.
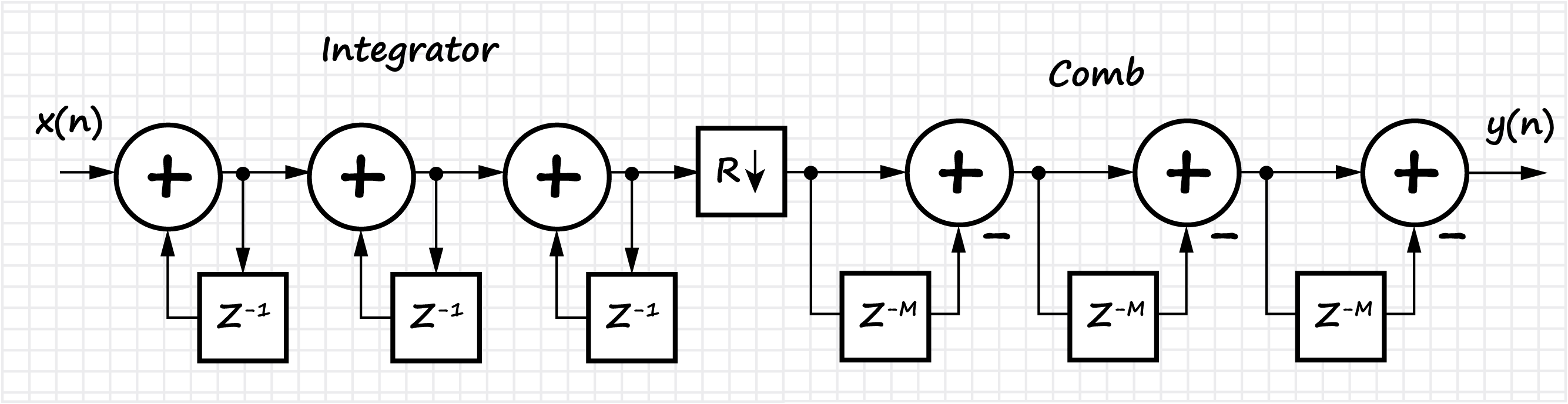
Graph of the frequency response of the filter, depending on the decimation factor:
Also in this section, the issue of increasing the data width at the output of the CIC filter is discussed depending on its parameters. This is especially important in the tasks of software implementation, in particular on the FPGA.
For the practical implementation of CIC filters in Python, a separate class CicFilter has been developed that implements the methods of decimation and interpolation. Examples of changing the sample rate using built-in methods from the Python scipy package are also shown.
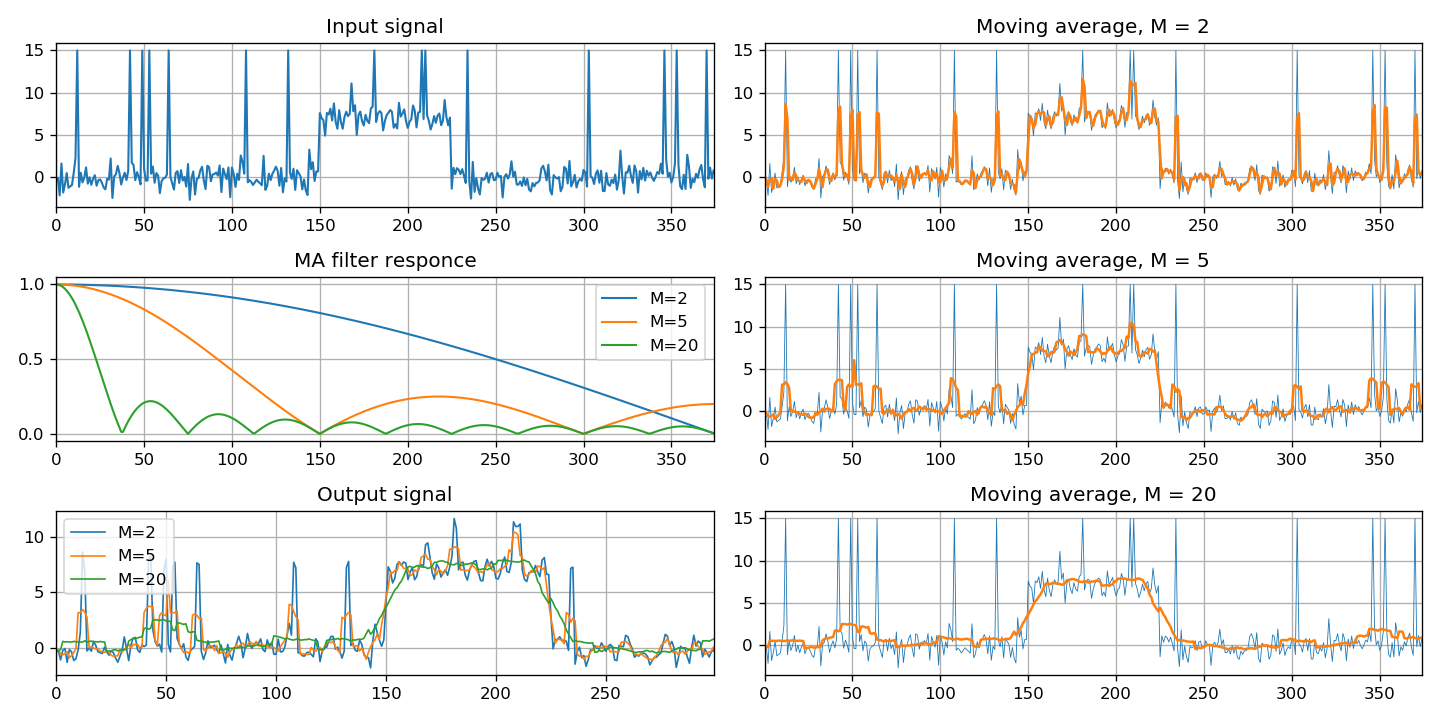
Finally, this section presents a special class of filters - the moving average. Three ways of implementation are shown: through convolution of signals, using an FIR filter and an IIR filter.
I hope this course of lectures in conjunction with my previous articles on digital signal processing on FPGA will bring practical benefits and help the reader better understand the basics of digital signal processing. This project will be improved and complemented by new useful and equally interesting material. Follow the development!
In addition to this material, I support and develop my project on the main DSP modules (in Python). It contains a package for generating various signals, a class of CIC filters for decimation and interpolation problems, an algorithm for calculating correction coefficients of an FIR filter, a moving average filter, an algorithm for calculating an over-long FFT through two-dimensional transformation methods (the latter is very useful in hardware implementation on the FPGA) .
Thanks for attention!
I am often approached by people with questions on problems in the field of digital signal processing (DSP). I tell in detail the nuances, suggest the necessary sources of information. But, as time has shown, all listeners lack practical tasks and examples in the process of learning this area. In this regard, I decided to write a short online course on digital signal processing and put it in open access .
Most of the training material for visual and interactive presentation is implemented using Jupyter Notebook . It is assumed that the reader has a basic knowledge of higher mathematics, and also knows a little programming language Python.
')

List of lectures
This course contains materials in the form of complete lectures on various topics in the field of digital signal processing. Materials are presented using Python libraries (numpy, scipy, matplotlib, etc.). The main information for this course is taken from my lectures, which I, as a graduate student, read to students of the Moscow Energy Institute (NIU MEI). Part of the information from these lectures was used at training seminars at the Center for Modern Electronics , where I acted as a lecturer. In addition, this material includes the translation of various scientific articles, compilation of information from reliable sources and literature on the subject of digital signal processing, as well as official documentation on the application packages and built-in functions of the scipy and numpy libraries of the Python language.
For users of MATLAB (GNU Octave), mastering the material in terms of program code is not difficult, since the main functions and their attributes are largely identical and similar to the methods from the Python libraries.
All materials are grouped by the main topics of digital signal processing:
- Signals: analog, discrete, digital. Z-transform
- Fourier transform: amplitude and phase signal, DFT and FFT,
- Convolution and correlation. Linear and cyclic convolution. Fast convolution
- Random processes. White noise. Probability density function
- Deterministic signals. Modulation: AM, FM, FM, chirp. Manipulation
- Signal filtering: IIR, FIR filters
- Window functions in filtering problems. Detection of weak signals.
- Resampling: decimation and interpolation. CIC filters, moving average filters
The list of lectures is sufficient
Where to find?
All materials are absolutely free and available as an open repository on my githaba as an opensource project . The materials are presented in two formats - in the form of notebooks Jupyter Notebook for interactive work, study and editing, and in the form of HTML files compiled from these notebooks (after downloading from the github they have quite a suitable format for reading and printing).
Below is a very brief description of the course sections with some explanations, terms and definitions. Basic information is available in the original lectures, here is only a brief overview!
Signals. Z-transform
The introductory section, which contains basic information on the types of signals. The concept of a discrete sequence, delta functions and Heaviside functions (a single jump) is introduced.
All signals according to the method of representation on the set can be divided into four groups:
- analog - described by continuous functions in time,
- discrete - interrupted in time with a step specified discretization,
- quantized - have a set of final levels (as a rule, in amplitude),
- digital - a combination of properties of discrete and quantized signals.

To correctly restore an analog signal from digital without distortion and loss, a sampling theorem known as the Kotelnikov (Nyquist-Shannon) theorem is used.
Any continuous signal with a limited spectrum can be recovered unambiguously and without loss in its discrete readings taken at a frequency strictly greater than twice the upper frequency of the spectrum of the continuous signal.
Such an interpretation is valid provided that the continuous function of time occupies a frequency band from 0 to the value of the upper frequency. If the quantization and sampling steps are chosen incorrectly, the conversion of the signal from analog to discrete form will occur with distortion.
Also in this section Z-transformation and its properties are described, the representation of discrete sequences in Z-form is shown.
Example of a finite discrete sequence:
x(nT) = {2, 1, -2, 0, 2, 3, 1, 0} An example of the same sequence in Z-form:
X (z) = 2 + z -1 - 2z -2 + 2z -4 + 3z -5 + 1z -6
Fourier transform. Properties DFT and FFT
This section describes the concept of the time and frequency domain of a signal. The definition of the discrete Fourier transform (DFT) is introduced. Considered direct and inverse DFT, their main properties. The transition from the DFT to the fast Fourier transform (FFT) algorithm at base 2 (frequency and time decimation algorithms) is shown. Reflects the effectiveness of the FFT in comparison with the DFT.
In particular, this section describes the Python package scipy.ffpack for computing various Fourier transforms (sine, cosine, direct, inverse, multidimensional, real).
Fourier transform allows you to represent any function as a set of harmonic signals! The Fourier transform underlies the convolution methods and the design of digital correlators, is actively used in spectral analysis, and is used when working with long numbers.
Features of the spectra of discrete signals:
1. The spectral density of a discrete signal is a periodic function with a period equal to the sampling frequency.
2. If the discrete sequence is real , then the modulus of the spectral density of such a sequence is an even function, and the argument is an odd function of frequency.
Harmonic spectrum:

Comparison of the effectiveness of DFT and FFT
The effectiveness of the FFT algorithm and the number of operations performed linearly depends on the length of the sequence N:
| N | DFT | FFT | The ratio of the number of complex additions | The ratio of the number of complex multiplications | ||
|---|---|---|---|---|---|---|
| The number of multiplication operations | The number of additions | The number of multiplication operations | The number of additions | |||
| 2 | four | 2 | one | 2 | four | one |
| four | sixteen | 12 | four | eight | four | 1.5 |
| eight | 64 | 56 | 12 | 24 | 5.3 | 2.3 |
| sixteen | 256 | 240 | 32 | 64 | eight | 3.75 |
| 32 | 1024 | 992 | 80 | 160 | 12.8 | 6.2 |
| 64 | 4096 | 4032 | 192 | 384 | 21.3 | 10.5 |
| 128 | 16384 | 16256 | 448 | 896 | 36.6 | 18.1 |
| ... | ... | ... | ... | ... | ... | ... |
| 4096 | 16777216 | 16773120 | 24576 | 49152 | 683 | 341 |
| 8192 | 67108864 | 67100672 | 53248 | 106496 | 1260 | 630 |
As you can see, the longer the conversion, the greater the savings in computing resources (in terms of processing speed or the number of hardware blocks)!
Any arbitrary waveform can be represented as a set of harmonic signals of different frequencies. In other words, a complex waveform in the time domain has a set of complex samples in the frequency domain, which are called * harmonics *. These readings express the amplitude and phase of the harmonic impact at a specific frequency. The larger the set of harmonics in the frequency domain, the more accurate the signal of complex shape.

Convolution and correlation
This section introduces the notion of correlation and convolution for discrete random and deterministic sequences. The connection of the autocorrelation and mutual correlation functions with convolution is shown. The properties of convolution are described, in particular, methods of linear and cyclic convolution of a discrete signal with detailed analysis are considered using the example of a discrete sequence. In addition, a method for calculating “fast” convolution using FFT algorithms is shown.
In real problems, it is often asked about the degree of similarity of one process to another, or about the independence of one process from another. In other words, it is required to determine the relationship between the signals, that is, to find a correlation . Correlation methods are used in a wide range of tasks: signal searching, computer vision and image processing, in radar tasks to determine the characteristics of targets and determine the distance to an object. In addition, using the correlation search for weak signals in the noise.
Convolution describes the interaction of signals with each other. If one of the signals is the impulse response of the filter, then the convolution of the input sequence with the impulse response is nothing like the response of the circuit to an input. In other words, the resulting signal reflects the signal passing through the filter.
Autocorrelation function (ACF) is used in coding information. The choice of the coding sequence according to the parameters of length, frequency and shape is largely due to the correlation properties of this sequence. The best code sequence has the lowest probability of false detection or response (for detecting signals, for threshold devices) or false synchronization (for transmitting and receiving code sequences).
This section presents a table comparing the efficiency of fast convolution and convolution calculated by a direct formula (the number of real multiplications).
As you can see, for FFT lengths up to 64, fast convolution loses from the direct method. However, with an increase in the length of the FFT, the results change in the opposite direction — fast convolution begins to outperform the direct method. Obviously, the greater the length of the FFT, the better the gain of the frequency method.
| N | Convolution | Fast convolution | Attitude |
|---|---|---|---|
| eight | 64 | 448 | 0.14 |
| sixteen | 256 | 1088 | 0.24 |
| 32 | 1024 | 2560 | 0.4 |
| 64 | 4096 | 5888 | 0.7 |
| 128 | 16K | 13312 | 1.23 |
| ... | ... | .. | ... |
| 2048 | 4M | 311296 | 13.5 |
Random signals and noise
In this section we introduce the concept of random signals, the density of the probability distribution, the law of distribution of a random variable. Mathematical moments are considered - the mean (expected value) and the variance (or the root of this quantity is the standard deviation). Also in this section we consider the normal distribution and the concept of white noise associated with it, as the main source of noise (interference) in signal processing.
A random signal is a function of time, the values of which are unknown in advance and can be predicted only with a certain probability . The main characteristics of random signals include:
- distribution law (relative time of a signal's value in a certain interval),
- spectral power distribution of the signal.

In DSP tasks, random signals are divided into two classes:
- noise - random fluctuations, consisting of a set of different frequencies and amplitudes,
- Signals that carry information for which processing it is required to resort to probabilistic methods.
Using random variables, it is possible to simulate the effect of a real medium on the passage of a signal from a source to a data receiver. When a signal passes through a noisy link, so-called white noise is added to the signal. As a rule, the spectral density of such noise is uniformly (equally) distributed at all frequencies, and the noise values in the time domain are normally distributed (Gaussian distribution law). Since white noise is physically added to the amplitudes of the signal at selected time samples, it is called additive white Gaussian noise (AWGN).
Signals, modulation and manipulation
This section shows the main ways to change one or more parameters of a harmonic signal. The concepts of amplitude, frequency and phase modulation are introduced. In particular, linear frequency modulation applied in radar tasks is highlighted. The main characteristics of the signals, the spectra of the modulated signals depending on the modulation parameters are shown.

For convenience, Python has created a set of functions that implement the listed types of modulation. An example of the implementation of the chirp signal:
def signal_chirp(amp=1.0, freq=0.0, beta=0.25, period=100, **kwargs): """ Create Chirp signal Parameters ---------- amp : float Signal magnitude beta : float Modulation bandwidth: beta < N for complex, beta < 0.5N for real freq : float or int Linear frequency of signal period : integer Number of points for signal (same as period) kwargs : bool Complex signal if is_complex = True Modulated by half-sine wave if is_modsine = True """ is_complex = kwargs.get('is_complex', False) is_modsine = kwargs.get('is_modsine', False) t = np.linspace(0, 1, period) tt = np.pi * (freq * t + beta * t ** 2) if is_complex is True: res = amp * (np.cos(tt) + 1j * np.sin(tt)) else: res = amp * np.cos(tt) if is_modsine is True: return res * np.sin(np.pi * t) return res 
Also in this section from the theory of transmission of discrete messages describes the types of digital modulation - manipulation. As in the case of analog signals, digital harmonic sequences can be manipulated in amplitude, phase and frequency (or in several parameters at once).

Digital filters - IIR and KIH
A large enough section on digital filtering of discrete sequences. In digital signal processing tasks, data passes through circuits called filters . Digital filters, like analog ones, have different characteristics — frequency response: frequency response, phase response, time response: impulse response, and filter response. Digital filters are used primarily to improve the quality of the signal — to extract a signal from a data sequence, or to degrade unwanted signals — to suppress certain signals in incoming sample sequences.

The section lists the main advantages and disadvantages of digital filters (compared to analog filters). The concept of impulse and transfer filter characteristics is introduced. Two classes of filters are considered - with infinite impulse response (IIR) and finite impulse response (FIR). A method of designing filters in canonical and direct form is shown. For FIR filters, the question of how to transition to a recursive form is considered.

For FIR filters, the filter design process is shown from the development stage of the technical specification (with indication of the main parameters), to the software and hardware implementation - search for filter coefficients (taking into account the form of number representation, data length, etc.). The definitions of symmetric FIR filters, linear phase response and its connection with the concept of group delay are introduced.

Window functions in filtering tasks
In the tasks of digital signal processing, window functions of various forms are used, which, when applied to a signal in the time domain, allow to qualitatively improve its spectral characteristics. A large number of various windows is primarily due to one of the main features of any window overlay. This feature is expressed in the relationship between the level of side lobes and the width of the central lobe. Rule:
The stronger the suppression of the side lobes of the spectrum, the wider the main lobe of the spectrum and vice versa.

One of the applications of window functions: the detection of weak signals against the background of stronger by suppressing the level of side lobes. The main window functions in DSP tasks are ** triangular, sinusoidal, Lanczos window, Hannah, Hamming, Blackman, Harris, Blackman-Harris, flat top window, Natall, Gauss, Kaiser ** window and many others. Most of them are expressed in a finite series by summing up the harmonic signals with specific weighting factors. Such signals are perfectly implemented in practice on any hardware devices (programmable logic circuits or signal processors).

Resampling. Decimation and interpolation
This section deals with multi-speed signal processing — changes in the sampling rate. Multirate processing of signals (multirate processing) assumes that in the process of linear conversion of digital signals it is possible to change the sampling frequency in the direction of reduction, increase or fractional number of times. This leads to more efficient signal processing, as it opens up the possibility of using the minimum allowable sampling rates and, as a consequence, a significant reduction in the required computing performance of the designed digital system.
Decimation (thinning) - lowering the sampling rate. Interpolation - increasing the sampling rate.
The section also discusses a class of homogeneous FIR filters, which are called integral-comb filters (CIC, Cascaded integrator – comb). The implementation, basic properties and features of CIC filters are shown. Due to the linearity of mathematical operations occurring in the CIC filter, a cascade connection of several filters in a row is possible, which gives a proportional decrease in the side lobe level, but also increases the main lobe of the amplitude-frequency characteristic.

Graph of the frequency response of the filter, depending on the decimation factor:

Also in this section, the issue of increasing the data width at the output of the CIC filter is discussed depending on its parameters. This is especially important in the tasks of software implementation, in particular on the FPGA.
For the practical implementation of CIC filters in Python, a separate class CicFilter has been developed that implements the methods of decimation and interpolation. Examples of changing the sample rate using built-in methods from the Python scipy package are also shown.
Python CicFilter Class for Digital Signal Processing
class CicFilter: """ Cascaded Integrator-Comb (CIC) filter is an optimized class of finite impulse response (FIR) filter. CIC filter combines an interpolator or decimator, so it has some parameters: R - decimation or interpolation ratio, N - number of stages in filter (or filter order) M - number of samples per stage (1 or 2)* * for this realisation of CIC filter just leave M = 1. CIC filter is used in multi-rate processing. In hardware applications CIC filter doesn't need multipliers, just only adders / subtractors and delay lines. Equation for 1st order CIC filter: y[n] = x[n] - x[n-RM] + y[n-1]. Parameters ---------- x : np.array input signal """ def __init__(self, x): self.x = x def decimator(self, r, n): """ CIC decimator: Integrator + Decimator + Comb Parameters ---------- r : int decimation rate n : int filter order """ # integrator y = self.x[:] for i in range(n): y = np.cumsum(y) # decimator y = y[::r] # comb stage return np.diff(y, n=n, prepend=np.zeros(n)) def interpolator(self, r, n, mode=False): """ CIC inteprolator: Comb + Decimator + Integrator Parameters ---------- r : int interpolation rate n : int filter order mode : bool False - zero padding, True - value padding. """ # comb stage y = np.diff(self.x, n=n, prepend=np.zeros(n), append=np.zeros(n)) # interpolation if mode: y = np.repeat(y, r) else: y = np.array([i if j == 0 else 0 for i in y for j in range(r)]) # integrator for i in range(n): y = np.cumsum(y) if mode: return y[1:1 - n * r] else: return y[r - 1:-n * r + r - 1] 
Finally, this section presents a special class of filters - the moving average. Three ways of implementation are shown: through convolution of signals, using an FIR filter and an IIR filter.

Conclusion
I hope this course of lectures in conjunction with my previous articles on digital signal processing on FPGA will bring practical benefits and help the reader better understand the basics of digital signal processing. This project will be improved and complemented by new useful and equally interesting material. Follow the development!
In addition to this material, I support and develop my project on the main DSP modules (in Python). It contains a package for generating various signals, a class of CIC filters for decimation and interpolation problems, an algorithm for calculating correction coefficients of an FIR filter, a moving average filter, an algorithm for calculating an over-long FFT through two-dimensional transformation methods (the latter is very useful in hardware implementation on the FPGA) .
Thanks for attention!
Source: https://habr.com/ru/post/460445/
All Articles