Pyramid sorting (HeapSort)

The translation of the article was prepared specifically for students of the Algorithms for Developers course.

Pyramid sorting (or heap sort, HeapSort) is a comparison sorting method based on a binary heap data structure. It is similar to sorting by choosing where we first look for the maximum element and put it at the end. Next, we repeat the same operation for the remaining elements.

What is a binary heap ?

Let's first define a complete binary tree. A complete binary tree is a binary tree in which each level, with the possible exception of the last, has a complete set of nodes, and all the leaves are located as far as possible to the left (Source Wikipedia ).

A binary heap is a complete binary tree in which elements are stored in a special order: the value in the parent node is greater (or less) than the values in its two child nodes. The first option is called max-heap, and the second is min-heap. A heap can be a binary tree or an array.

Why is an array-based view used for a binary heap?

Since the binary heap is a complete binary tree, it can easily be represented as an array, and the array-based representation is efficient in terms of memory consumption. If the parent node is stored in index I, the left child element can be calculated as 2 I + 1, and the right child element as 2 I + 2 (provided that the indexing starts from 0).

Algorithm of pyramid sorting in ascending order:

Build max-heap from input.
At this stage, the largest item is stored in the root of the heap. Replace it with the last element of the heap, and then reduce its size by 1. Finally, convert the resulting tree to max-heap with a new root.
Repeat the above steps until the heap size is greater than 1.

How to build a bunch?

The heap-convert procedure (hereinafter the heapify procedure) can be applied to a node only if its child nodes have already been converted. Thus, the conversion must be performed from bottom to top. Let's understand with the help of an example:

 : 4, 10, 3, 5, 1 4(0) / \ 10(1) 3(2) / \ 5(3) 1(4)           .   heapify   1: 4(0) / \ 10(1) 3(2) / \ 5(3) 1(4)   heapify   0: 10(0) / \ 5(1) 3(2) / \ 4(3) 1(4)  heapify        .

Recommendation: Please solve the “PRACTICE” problem first, before proceeding to the solution .

C ++

 //     C++ #include <iostream> using namespace std; //           i,   //   arr[]. n -   void heapify(int arr[], int n, int i) { int largest = i; //      int l = 2*i + 1; //  = 2*i + 1 int r = 2*i + 2; //  = 2*i + 2 //       if (l < n && arr[l] > arr[largest]) largest = l; //     ,        if (r < n && arr[r] > arr[largest]) largest = r; //       if (largest != i) { swap(arr[i], arr[largest]); //        heapify(arr, n, largest); } } //  ,    void heapSort(int arr[], int n) { //   ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); //        for (int i=n-1; i>=0; i--) { //      swap(arr[0], arr[i]); //   heapify    heapify(arr, i, 0); } } /*         n*/ void printArray(int arr[], int n) { for (int i=0; i<n; ++i) cout << arr[i] << " "; cout << "\n"; } //   int main() { int arr[] = {12, 11, 13, 5, 6, 7}; int n = sizeof(arr)/sizeof(arr[0]); heapSort(arr, n); cout << "Sorted array is \n"; printArray(arr, n); }

Java

 //     Java public class HeapSort { public void sort(int arr[]) { int n = arr.length; //   ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); //        for (int i=n-1; i>=0; i--) { //      int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; //   heapify    heapify(arr, i, 0); } } //           i,   //   arr[]. n -   void heapify(int arr[], int n, int i) { int largest = i; //      int l = 2*i + 1; //  = 2*i + 1 int r = 2*i + 2; //  = 2*i + 2 //       if (l < n && arr[l] > arr[largest]) largest = l; //     ,        if (r < n && arr[r] > arr[largest]) largest = r; //       if (largest != i) { int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; //        heapify(arr, n, largest); } } /*         n */ static void printArray(int arr[]) { int n = arr.length; for (int i=0; i<n; ++i) System.out.print(arr[i]+" "); System.out.println(); } //   public static void main(String args[]) { int arr[] = {12, 11, 13, 5, 6, 7}; int n = arr.length; HeapSort ob = new HeapSort(); ob.sort(arr); System.out.println("Sorted array is"); printArray(arr); } }

Python

 #     Python #           i,     arr[]. n -   def heapify(arr, n, i): largest = i # Initialize largest as root l = 2 * i + 1 # left = 2*i + 1 r = 2 * i + 2 # right = 2*i + 2 #       ,   if l < n and arr[i] < arr[l]: largest = l #       ,   if r < n and arr[largest] < arr[r]: largest = r #  ,   if largest != i: arr[i],arr[largest] = arr[largest],arr[i] #  #  heapify  . heapify(arr, n, largest) #        def heapSort(arr): n = len(arr) #  max-heap. for i in range(n, -1, -1): heapify(arr, n, i) #      for i in range(n-1, 0, -1): arr[i], arr[0] = arr[0], arr[i] #  heapify(arr, i, 0) #     arr = [ 12, 11, 13, 5, 6, 7] heapSort(arr) n = len(arr) print ("Sorted array is") for i in range(n): print ("%d" %arr[i]), #    Mohit Kumra

C sharp

 //     C# using System; public class HeapSort { public void sort(int[] arr) { int n = arr.Length; //   ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); //        for (int i=n-1; i>=0; i--) { //      int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; //   heapify    heapify(arr, i, 0); } } //           i,   //   arr[]. n -   void heapify(int[] arr, int n, int i) { int largest = i; //      int l = 2*i + 1; // left = 2*i + 1 int r = 2*i + 2; // right = 2*i + 2 //       if (l < n && arr[l] > arr[largest]) largest = l; //     ,        if (r < n && arr[r] > arr[largest]) largest = r; //       if (largest != i) { int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; //        heapify(arr, n, largest); } } /*         n */ static void printArray(int[] arr) { int n = arr.Length; for (int i=0; i<n; ++i) Console.Write(arr[i]+" "); Console.Read(); } //  public static void Main() { int[] arr = {12, 11, 13, 5, 6, 7}; int n = arr.Length; HeapSort ob = new HeapSort(); ob.sort(arr); Console.WriteLine("Sorted array is"); printArray(arr); } } //   // Akanksha Ra (Abby_akku)

Php

 <?php //     Php //           i,   //   arr[]. n -   function heapify(&$arr, $n, $i) { $largest = $i; //      $l = 2*$i + 1; //  = 2*i + 1 $r = 2*$i + 2; //  = 2*i + 2 //       if ($l < $n && $arr[$l] > $arr[$largest]) $largest = $l; //    ,        if ($r < $n && $arr[$r] > $arr[$largest]) $largest = $r; //       if ($largest != $i) { $swap = $arr[$i]; $arr[$i] = $arr[$largest]; $arr[$largest] = $swap; //        heapify($arr, $n, $largest); } } // ,    function heapSort(&$arr, $n) { //   ( ) for ($i = $n / 2 - 1; $i >= 0; $i--) heapify($arr, $n, $i); //       for ($i = $n-1; $i >= 0; $i--) { //      $temp = $arr[0]; $arr[0] = $arr[$i]; $arr[$i] = $temp; //   heapify    heapify($arr, $i, 0); } } /*         n */ function printArray(&$arr, $n) { for ($i = 0; $i < $n; ++$i) echo ($arr[$i]." ") ; } //   $arr = array(12, 11, 13, 5, 6, 7); $n = sizeof($arr)/sizeof($arr[0]); heapSort($arr, $n); echo 'Sorted array is ' . "\n"; printArray($arr , $n); //    Shivi_Aggarwal ?>

Conclusion:

  : 5 6 7 11 12 13

Here is the previous C code for reference.

Remarks:
Pyramid sorting is a perfectly valid algorithm. Its typical implementation is not stable, but it can be made as such (see here ).

Time complexity: Time complexity heapify - O (Logn). The time complexity of createAndBuildHeap () is O (n), and the total time of pyramid sorting is O (nLogn).

Pyramid sorting applications:

The pyramid sorting algorithm is of limited use because Quicksort (Quick Sort) and Mergesort (Sort Merge) are better in practice. However, the heap data structure itself is used quite often. See Heap Data Structure Applications .

Screenshots: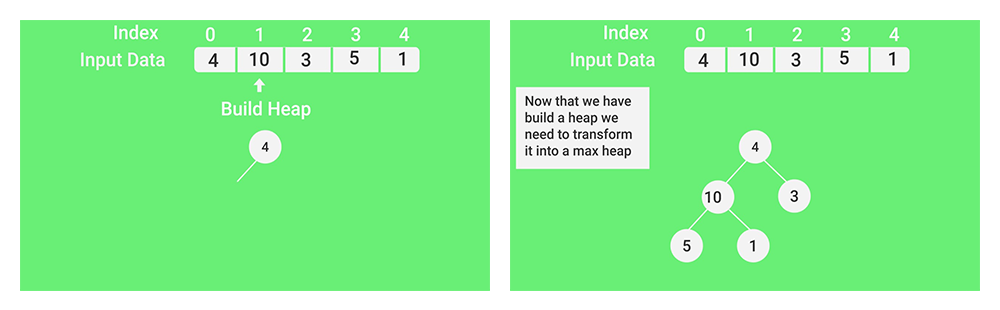

- (Now that we have built the heap, we need to convert it to max-heap)

- (In max-heap, the parent node is always greater than or equal to the children
10 more 4. Therefore, we swap 4 and 10)
- (In max-heap, the parent node is always greater than or equal to the children
5 more 4. For this we change places 5 and 4)