B-tree data structure
Hello! We have launched a new recruitment for the Algorithms for Developers course and today we want to share an interesting translation prepared for the students of this course.

In search trees, such as binary search tree, AVL tree, red-ebony, etc. Each node contains only one value (key) and a maximum of two descendants. However, there is a special type of search tree called a B-tree (pronounced Bi-Tree). In it the node contains more than one value (key) and more than two descendants. The B-tree was developed in 1972 by Bayer and McCreit and was called Height Balanced Search Tree of order m (Height Balanced m-way Search Tree) . Its modern name B-tree received later.
')
B-tree can be defined as follows:
A B-tree is a balanced search tree, in which each node contains multiple keys and has more than two descendants.
Here the number of keys in the node and the number of its descendants depends on the order of the B-tree. Every B-tree has an order.
The b-tree of order m has the following properties:
Property 1: The depth of all leaves is the same.
Property 2: All nodes except the root must have at least (m / 2) - 1 keys and a maximum of m-1 keys.
Property 3: All nodes without leaves, except the root (ie, all internal nodes) must have at least m / 2 descendants.
Property 4: If the root is a node containing no leaves, it must have at least 2 descendants.
Property 5: A node without leaves with n-1 keys must have n descendants.
Property 6: All keys in a node must be in ascending order of their values.
For example, a 4-order B-tree contains a maximum of 3 key values and a maximum of 4 children for each node.
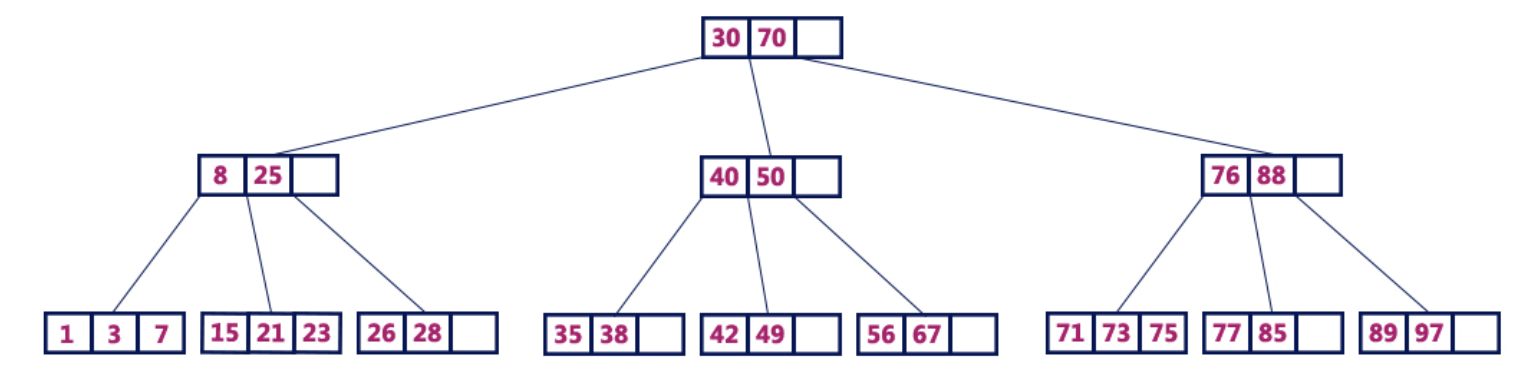
B-tree 4 orders
B-tree operations
The following operations can be performed on a B-tree:
B-tree search
Search in a B-tree is similar to a search in a binary search tree. In the binary search tree, the search starts from the root and each time a two-way decision is made (go along the left subtree or along the right). In the B-tree, the search also begins with the root node, but at each step an n-sided decision is made, where n is the total number of descendants of the node in question. In the B-tree, the search complexity is O (log n) . The search is as follows:
Step 1: Count the item to search.
Step 2: Compare the item to the first key value in the root node of the tree.
Step 3: If they match, output: “The node was found!” And complete the search.
Step 4: If they do not match, check the element value more or less than the current key value.
Step 5: If the item you are looking for is smaller, continue searching the left subtree.
Step 6: If the item you are looking for is larger, compare the item with the next key value in the node and repeat Steps 3, 4, 5 and 6 until a match is found or until the desired item is compared with the last key value in the leaf node.
Step 7: If the last value of the key in the list node does not coincide with the required one, output “No item found!” And complete the search.
B-tree insert operation
In the B-tree, a new element can only be added to the list node. This means that a new key-value pair is always added only to the leaf node. The insertion is as follows:
Step 1: Check if the tree is empty.
Step 2: If the tree is empty, create a new node with a new key value and take it as the root node.
Step 3: If the tree is not empty, find the appropriate leaf node to which the new value will be added, using the logic of the binary search tree.
Step 4: If there is an unused cell in the current leaf node, add a new key value to the current leaf node, following the increasing order of key values inside the node.
Step 5: If the current node is full and has no free cells, divide the leaf node by sending the average value to the parent node. Repeat step until the value to be sent is fixed in the node.
Step 6: If the separation occurs with the root of the tree, then the average value becomes the new root of the tree and the height of the tree is increased by one.
Example:
Let's create a B-tree of order 3 by adding numbers from 1 to 10 to it.
Insert (1):
Since “1” is the first element of the tree, it is inserted into the new node and this node becomes the root of the tree.

Insert (2):
Element "2" is added to the existing list node. Now we have only one node, therefore it is both a root and a leaf at the same time. This sheet has an empty cell. Then "2" rises in this empty cell.

Insert (3):
Element "3" is added to the existing node list. Now we have only one node, which is both a root and a leaf. This sheet does not have an empty cell. Therefore, we divide this node by sending the average value (2) to the parent node. However, the current node has no parent node. Therefore, the average value becomes the root node of the tree.

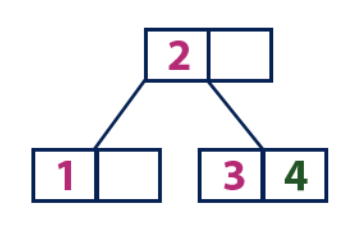
Insert (4):
Element "4" is greater than the root node with the value "2", and the root node is not a leaf. Therefore, we move along the right subtree of “2.” We come to the leaf node with the value "3", which has an empty cell. Thus, we can insert the element "4" in this empty cell.
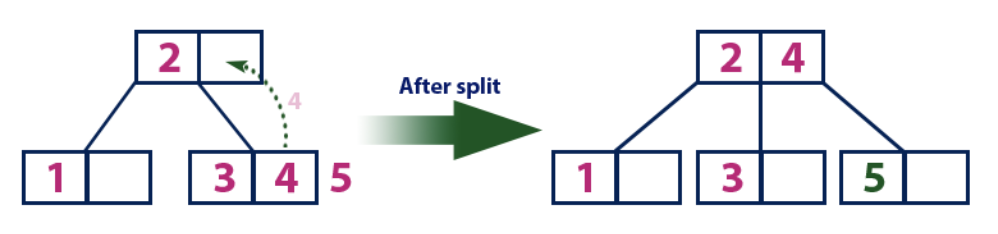
Insert (5):
Element "5" is greater than the root node with the value "2", and the root node is not a leaf. Therefore, we move along the right subtree of “2.” We arrive at a leaf node and find that it is already full and does not have empty cells. Then we divide this node by sending the mean (4) to the parent node (2). The parent node has an empty cell for it, so the value “4” is added to the node where the value 2 already exists, and the new element 5 is added as a new sheet.
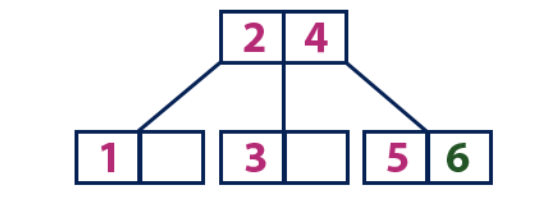
Insert (6):
Element "6" is larger than elements of the root "2" and "4", which is not a leaf. We move on the right subtree from the element "4". We reach a sheet with the value "5", which has an empty cell, so the element "6" is placed just in it.
Insert (7):
Element "7" is larger than the elements of the root "2" and "4", which is not a leaf. We move on the right subtree from the element "4". We reach the leaf node and see that it is full. We divide this node by sending the average value “6” up to the parent node with elements “2” and “4”. However, the parent node is also full, so we divide the node with the elements “2” and “4”, sending the value “4” to the parent node. Only this site is not yet. In this case, the node with the element "4" becomes the new root of the tree.
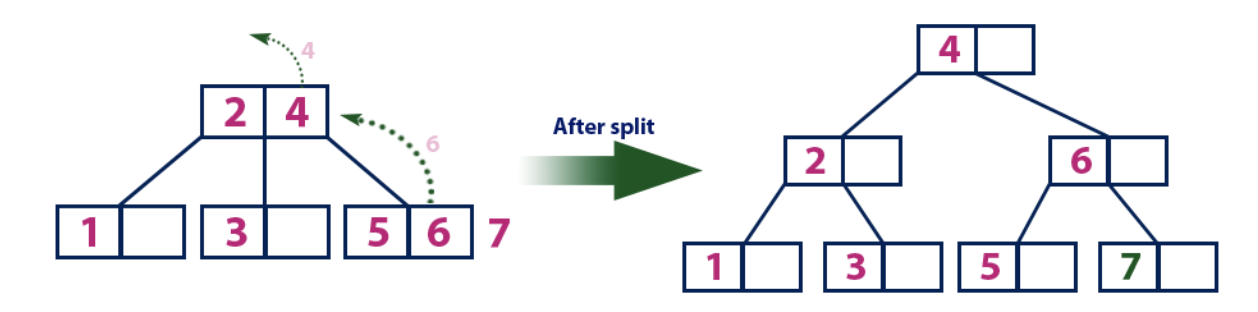
Insert (8):
Element "8" is greater than the root node with the value "4", and the root node is not a leaf. We move on the right subtree from the element “4” and arrive at the node with the value “6”. “8” is greater than “6” and the node with the element “6” is not a leaf, so we move along the right subtree from “6”. We reach the leaf node with "7", which has an empty cell, so we put "8" in it.
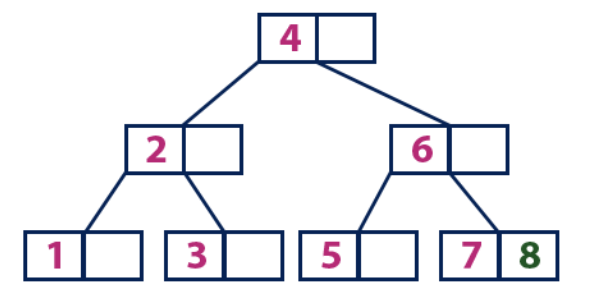
Insert (9):
Element "9" is greater than the root node with the value "4", and the root node is not a leaf. We move on the right subtree from the element “4” and arrive at the node with the value “6”. “9” is greater than “6” and the node with the element “6” is not a leaf, so we move along the right subtree from “6”. We reach the node list with the values "7" and "8". He is full. We divide this node by sending the average value (8) to the parent node. The parent node "6" has an empty cell, so we put "8" in it. At the same time, the new element “9” is added to the list node.
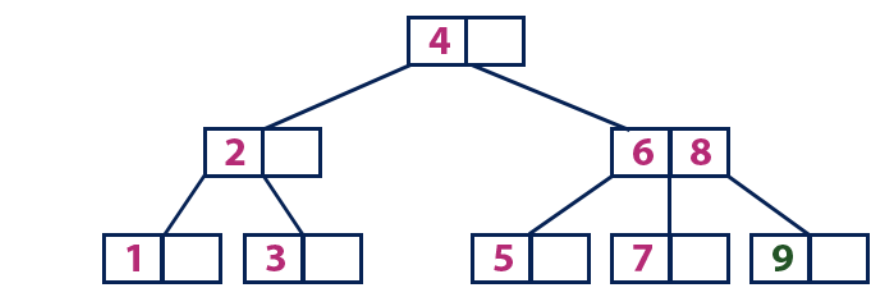
Insert (10):
Element "10" is greater than the root node with the value "4", and the root node is not a leaf. We move on the right subtree from the element “4” and arrive at the node with the values “6” and “8”. “10” is greater than “6” and “8” and the node with these elements is not a leaf, so we move along the right subtree from “8.” We reach the leaf node with the value "9". He has an empty cell, so we put "10" there.
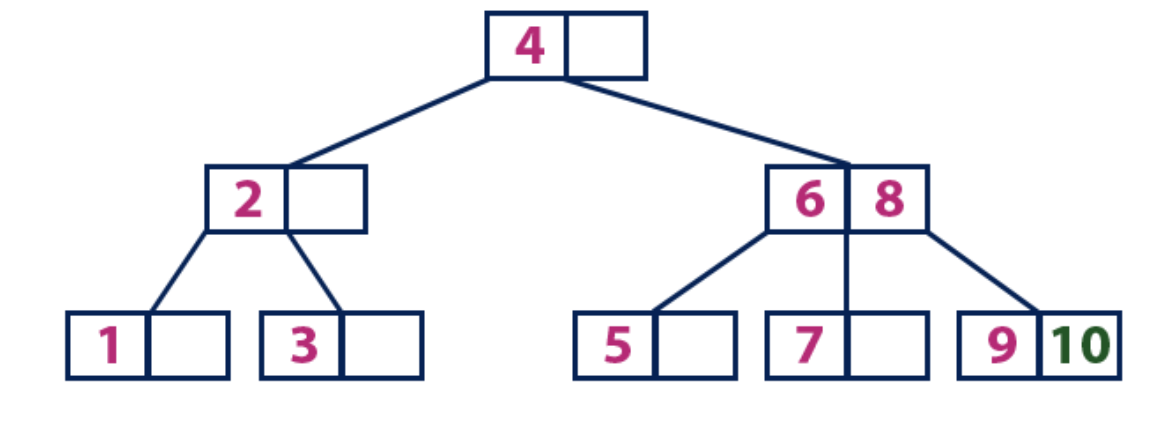
We suggest that you independently understand in practice how the B-trees are arranged, using this visualization .
We are waiting for everyone in the free open lesson , which will be held on July 12. See you!

In search trees, such as binary search tree, AVL tree, red-ebony, etc. Each node contains only one value (key) and a maximum of two descendants. However, there is a special type of search tree called a B-tree (pronounced Bi-Tree). In it the node contains more than one value (key) and more than two descendants. The B-tree was developed in 1972 by Bayer and McCreit and was called Height Balanced Search Tree of order m (Height Balanced m-way Search Tree) . Its modern name B-tree received later.
')
B-tree can be defined as follows:
A B-tree is a balanced search tree, in which each node contains multiple keys and has more than two descendants.
Here the number of keys in the node and the number of its descendants depends on the order of the B-tree. Every B-tree has an order.
The b-tree of order m has the following properties:
Property 1: The depth of all leaves is the same.
Property 2: All nodes except the root must have at least (m / 2) - 1 keys and a maximum of m-1 keys.
Property 3: All nodes without leaves, except the root (ie, all internal nodes) must have at least m / 2 descendants.
Property 4: If the root is a node containing no leaves, it must have at least 2 descendants.
Property 5: A node without leaves with n-1 keys must have n descendants.
Property 6: All keys in a node must be in ascending order of their values.
For example, a 4-order B-tree contains a maximum of 3 key values and a maximum of 4 children for each node.

B-tree 4 orders
B-tree operations
The following operations can be performed on a B-tree:
- Search
- Insert
- Deletion
B-tree search
Search in a B-tree is similar to a search in a binary search tree. In the binary search tree, the search starts from the root and each time a two-way decision is made (go along the left subtree or along the right). In the B-tree, the search also begins with the root node, but at each step an n-sided decision is made, where n is the total number of descendants of the node in question. In the B-tree, the search complexity is O (log n) . The search is as follows:
Step 1: Count the item to search.
Step 2: Compare the item to the first key value in the root node of the tree.
Step 3: If they match, output: “The node was found!” And complete the search.
Step 4: If they do not match, check the element value more or less than the current key value.
Step 5: If the item you are looking for is smaller, continue searching the left subtree.
Step 6: If the item you are looking for is larger, compare the item with the next key value in the node and repeat Steps 3, 4, 5 and 6 until a match is found or until the desired item is compared with the last key value in the leaf node.
Step 7: If the last value of the key in the list node does not coincide with the required one, output “No item found!” And complete the search.
B-tree insert operation
In the B-tree, a new element can only be added to the list node. This means that a new key-value pair is always added only to the leaf node. The insertion is as follows:
Step 1: Check if the tree is empty.
Step 2: If the tree is empty, create a new node with a new key value and take it as the root node.
Step 3: If the tree is not empty, find the appropriate leaf node to which the new value will be added, using the logic of the binary search tree.
Step 4: If there is an unused cell in the current leaf node, add a new key value to the current leaf node, following the increasing order of key values inside the node.
Step 5: If the current node is full and has no free cells, divide the leaf node by sending the average value to the parent node. Repeat step until the value to be sent is fixed in the node.
Step 6: If the separation occurs with the root of the tree, then the average value becomes the new root of the tree and the height of the tree is increased by one.
Example:
Let's create a B-tree of order 3 by adding numbers from 1 to 10 to it.
Insert (1):
Since “1” is the first element of the tree, it is inserted into the new node and this node becomes the root of the tree.

Insert (2):
Element "2" is added to the existing list node. Now we have only one node, therefore it is both a root and a leaf at the same time. This sheet has an empty cell. Then "2" rises in this empty cell.

Insert (3):
Element "3" is added to the existing node list. Now we have only one node, which is both a root and a leaf. This sheet does not have an empty cell. Therefore, we divide this node by sending the average value (2) to the parent node. However, the current node has no parent node. Therefore, the average value becomes the root node of the tree.

Insert (4):
Element "4" is greater than the root node with the value "2", and the root node is not a leaf. Therefore, we move along the right subtree of “2.” We come to the leaf node with the value "3", which has an empty cell. Thus, we can insert the element "4" in this empty cell.

Insert (5):
Element "5" is greater than the root node with the value "2", and the root node is not a leaf. Therefore, we move along the right subtree of “2.” We arrive at a leaf node and find that it is already full and does not have empty cells. Then we divide this node by sending the mean (4) to the parent node (2). The parent node has an empty cell for it, so the value “4” is added to the node where the value 2 already exists, and the new element 5 is added as a new sheet.

Insert (6):
Element "6" is larger than elements of the root "2" and "4", which is not a leaf. We move on the right subtree from the element "4". We reach a sheet with the value "5", which has an empty cell, so the element "6" is placed just in it.

Insert (7):
Element "7" is larger than the elements of the root "2" and "4", which is not a leaf. We move on the right subtree from the element "4". We reach the leaf node and see that it is full. We divide this node by sending the average value “6” up to the parent node with elements “2” and “4”. However, the parent node is also full, so we divide the node with the elements “2” and “4”, sending the value “4” to the parent node. Only this site is not yet. In this case, the node with the element "4" becomes the new root of the tree.

Insert (8):
Element "8" is greater than the root node with the value "4", and the root node is not a leaf. We move on the right subtree from the element “4” and arrive at the node with the value “6”. “8” is greater than “6” and the node with the element “6” is not a leaf, so we move along the right subtree from “6”. We reach the leaf node with "7", which has an empty cell, so we put "8" in it.

Insert (9):
Element "9" is greater than the root node with the value "4", and the root node is not a leaf. We move on the right subtree from the element “4” and arrive at the node with the value “6”. “9” is greater than “6” and the node with the element “6” is not a leaf, so we move along the right subtree from “6”. We reach the node list with the values "7" and "8". He is full. We divide this node by sending the average value (8) to the parent node. The parent node "6" has an empty cell, so we put "8" in it. At the same time, the new element “9” is added to the list node.

Insert (10):
Element "10" is greater than the root node with the value "4", and the root node is not a leaf. We move on the right subtree from the element “4” and arrive at the node with the values “6” and “8”. “10” is greater than “6” and “8” and the node with these elements is not a leaf, so we move along the right subtree from “8.” We reach the leaf node with the value "9". He has an empty cell, so we put "10" there.

We suggest that you independently understand in practice how the B-trees are arranged, using this visualization .
We are waiting for everyone in the free open lesson , which will be held on July 12. See you!
Source: https://habr.com/ru/post/459216/
All Articles