Grasshopper cryptographic algorithm: just about complicated
In this article, the block encryption algorithm defined in GOST R 34.12-2015 as βGrasshopperβ will be discussed in detail. What it is based on, what is the mathematics of block cryptoalgorithms, as well as how this algorithm is implemented in java.
Who, how, when and why has developed this algorithm will remain beyond the scope of the article, since in this case we are of little interest, except:
SMITH = Kuznetsov, Nechaev And Company.
')
Since cryptography is primarily based on mathematics, so that a further explanation does not cause a lot of questions, you should first understand the basic concepts and mathematical functions on which this algorithm is based.
The arithmetic of Galois fields is polynomial arithmetic, that is, each element of this field is a certain polynomial. The result of any operation is also an element of this field. A specific Galois field consists of a fixed range of numbers. A characteristic of the field is some prime p. Field order, i.e. the number of its elements is some natural degree of characteristic pm , where m Ο΅ N. For m = 1, the field is called simple. In cases when m> 1, a polynomial of degree m is needed to form a field, such a field is called extended. GF(pm) - Galois field designation. The generator polynomial is irreducible, that is, simple (by analogy with primes, it is divisible by 1 and by itself). Since working with any information is working with bytes, and byte is 8 bits, they take as a field GF(28) and generating polynomial:
However, to begin with, we will analyze the main operations in a simpler field. GF(23) with generating polynomial f(x)=x3+x+1 .
The simplest is the addition operation, which in the arithmetic of the Galois fields is a simple bitwise addition modulo 2 (XOR).
Immediately I draw attention to the fact that the β+β sign here and hereafter denotes the operation of bitwise XOR, and not addition in the usual form.
The truth table of the XOR function
Example: 5+3=101+011=1102=610
In a polynomial form, this operation will look like
To carry out the multiplication operation, it is necessary to convert numbers into a polynomial form:
As you can see a number in a polynomial form is a polynomial whose coefficients are the values ββof bits in the binary representation of a number.
Multiply two numbers in polynomial form:
The result of multiplication 27 is not included in the used field. GF(23) (it consists of numbers from 0 to 7, as mentioned above). To deal with this problem, you must use the generator polynomial.
It is also assumed that x satisfies the equation f(x)=x3+x+1=0 then
Let's make the multiplication table:
Of great importance is the table of degrees of elements of the Galois field. Exponentiation is also carried out in a polynomial form, similar to multiplication.
Example:
Thus, we make a table of degrees:
The degree table is cyclical: the seventh degree corresponds to zero, which means the eighth corresponds to the first, and so on. If you wish, you can check it out.
In Galois fields, there is the concept of a primitive member - a field element whose degrees contain all non-zero field elements. It can be seen that all the elements correspond to this condition (well, except for 1, of course). However, this is not always the case.
For the fields that we consider, that is, with characteristic 2, always choose 2 as the primitive member. Given its property, any element of the field can be expressed in terms of the degree of the primitive member.
Example: 5=26,7=25
Using this property, and taking into account the cyclical nature of the table of degrees, we will try to multiply the numbers again:
The result coincided with what we calculated earlier.
And now let's do the division:
The result obtained is also true.
Well, for completeness, let's look at the exponentiation:
Such an approach to multiplication and division is much simpler than real operations using polynomials, and for them there is no need to store a large multiplication table, but only a row of powers of a primitive field member is sufficient.
Now back to our field GF(28)
The zero element of the field is a unit, the 1st is a deuce, each subsequent element from the 2nd to the 254th is calculated as the previous one multiplied by 2, and if the element goes beyond the field, that is, its value is greater than (28β1) then xor is done with the number 19510 , this number represents an irreducible polynomial of a field. x8+x7+x6+x+1=28+27++26+2+1=451 , we will bring this number into the box 451β256=$19 . And the 255th element is again equal to 1. Thus, we have a field containing 256 elements, that is, a complete set of bytes, and we have analyzed the basic operations that are performed in this field.
The power of two for the field GF(28)
For what it was needed - part of the calculations in the Grasshopper algorithm are performed in the Galois field, and the results of the calculations, respectively, are elements of this field.
The Feistel network is a block encryption method developed by Horst Feistel in the IBM laboratory in 1971. Today, the Feistel network underlies a large number of cryptographic protocols.
The Feistel network operates with plaintext blocks:
This sequence of actions is called a Feistel cell.
Figure 1. Cell Feistel
The Feistel network consists of several cells. The subblocks obtained at the output of the first cell enter the input of the second cell, the resulting subblocks from the second cell enter the input of the third cell, and so on.
Now we are familiar with the operations used and can move on to the main topic - namely the Grasshopper cryptoalgorithm.
The basis of the algorithm is the so-called SP network - substitution-permutation network (Substitution-Permutationnetwork). The cipher based on the SP network receives a block and a key at the input and performs several alternating rounds consisting of substitution stages and permutation stages. In Grasshopper, there are nine complete rounds, each of which includes three successive operations:
The last tenth round is not complete, it includes only the first XOR operation.
Grasshopper is a block algorithm, it works with data blocks of 128 bits or 16 bytes in length. The key length is 256 bits (32 bytes).
Figure 2. Data block encryption and decryption scheme
The diagram shows the sequence of operations, where S is a nonlinear transformation, L is a linear transformation, Ki is round keys. The question immediately arises - where do the round keys come from?
Iterative (or round) keys are obtained by certain transformations based on the master key, the length of which, as we already know, is 256 bits. This process begins with splitting the master key in half, so the first pair of round keys is obtained. For the generation of each subsequent pair of round keys, eight iterations of the Feistel network are used, each iteration uses a constant, which is calculated by applying a linear transformation of the algorithm to the value of the iteration number.
The scheme of obtaining iterative (round) keys
If we recall Figure 1, then the left subblock L is the left half of the original key, the right subblock R is the right half of the original key, K is the Ci constant, f is the R sequence of operations XOR Ci, nonlinear transformation, linear transformation.
Iteration constants Ci are obtained using the L-transform of the iteration sequence number.
So, in order to encrypt a block of text, we first need to calculate 32 iteration constants, then, on the basis of the key, calculate 10 round keys, and then perform the sequence of operations shown in Figure 2.
Let's start by calculating the constants:
First constant C1=110=000000012=0116 However, all the transformations in our algorithm are performed with blocks of 16 bytes in length, so you need to add a constant to the block length, that is, add 15 null bytes to the right, we get
Multiply it by the row (1, 148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148) as follows:
(this equality is given in Galois field operations)
Since all but the zero byte are 0, and the zero byte is multiplied by 1, we get 1 and write it to the most significant digit of the number, moving all the bytes towards the least significant bit, we get:
Repeat the same operations. This time a15=1 , all other bytes are 0, therefore only the first of the terms remains. a15β148=1β148=14810=9416 we get:
We make the third iteration, here are two nonzero terms:
According to the degree table it could be solved much easier:
Then everything is exactly the same, only 16 iterations for each constant
And the final constant:
The remaining constants are:
Now we will calculate the round keys according to the scheme presented above, let's take the encryption key:
Then
K1 will be the left subblock of the Feistel network, and K2 - right.
Perform the operation K1+C1
First byte K1 equals 7716=011101112
First byte C1 equals 0116=000000012
the remaining bytes are converted similarly, in the end X(K1,C1)=K1+C1 :
Next, perform a nonlinear transformation S(X(K1,C1)) . It is performed according to the table:
Nonlinear conversion table
The number 0 is replaced by 252, 1 by 238, 17 by 119, etc.
Now let's do a linear transformation. L(S(X(K1,C1))) , it was considered in detail when calculating the iteration constants, so here we give only the final result:
According to the Feistel cell scheme, we will execute an XOR with the right sub-block, that is, with K2 :
And the result obtained at the output of the first Feistel cell:
This value is split in half and goes to the input of the second Feistel cell, where the second constant is already used. C2 . Having passed eight cells we will receive 2 following keys K3 and K4 . We run eight iterations of the Feistel network with them, we get the next pair of keys, and so on. There are eight iterations per pair of keys, since we have the first pair, there are 32 iterations in total, each with its own constant.
Remaining keys:
We calculated all the keys and now at last we can go directly to encrypting the block of text, and if you carefully read everything written above, then it will not be difficult to encrypt the text, since all the operations used and the sequence were examined in detail.
Take the plaintext block:
perform the sequence of operations X, S, L
and so on, the end result will look like this:
To decrypt text, you must use the inverse operations in reverse order (see. Fig. 2).
The XOR operation is inverse to itself, the inverse of operation S is the substitution according to the following table:
Inverse nonlinear transformation table
The inverse transform to the function L is:
and a shift towards higher order. (Repeat operation 16 times)
First we define the necessary constants.
Let's create all the main functions:
To implement the function L, we need several auxiliary functions, one for calculating the multiplication of numbers in the Galois field, and one for the shift.
Reverse functions:
Well, the main function
We have learned to encrypt a data block in order to encrypt text whose length is greater than the block length, there are several modes described in the standard - GOST 34.13-2015:
In all modes, the text length must always be a multiple of the block length, therefore the text is always padded to the right with one single bit and zeros to the block length.
The simplest mode is the simple replacement mode. In this mode, the text is divided into blocks, then each block is encrypted separately from the others, then the blocks of the encrypted text are glued together and we get an encrypted message. This mode is both the easiest and most vulnerable and almost never used in practice.
The remaining modes will probably be discussed in detail later.
Who, how, when and why has developed this algorithm will remain beyond the scope of the article, since in this case we are of little interest, except:
SMITH = Kuznetsov, Nechaev And Company.
')
Since cryptography is primarily based on mathematics, so that a further explanation does not cause a lot of questions, you should first understand the basic concepts and mathematical functions on which this algorithm is based.
Paul Galois
The arithmetic of Galois fields is polynomial arithmetic, that is, each element of this field is a certain polynomial. The result of any operation is also an element of this field. A specific Galois field consists of a fixed range of numbers. A characteristic of the field is some prime p. Field order, i.e. the number of its elements is some natural degree of characteristic pm , where m Ο΅ N. For m = 1, the field is called simple. In cases when m> 1, a polynomial of degree m is needed to form a field, such a field is called extended. GF(pm) - Galois field designation. The generator polynomial is irreducible, that is, simple (by analogy with primes, it is divisible by 1 and by itself). Since working with any information is working with bytes, and byte is 8 bits, they take as a field GF(28) and generating polynomial:
x8+x7+x6+x+1.
However, to begin with, we will analyze the main operations in a simpler field. GF(23) with generating polynomial f(x)=x3+x+1 .
Addition operation
The simplest is the addition operation, which in the arithmetic of the Galois fields is a simple bitwise addition modulo 2 (XOR).
Immediately I draw attention to the fact that the β+β sign here and hereafter denotes the operation of bitwise XOR, and not addition in the usual form.
The truth table of the XOR function
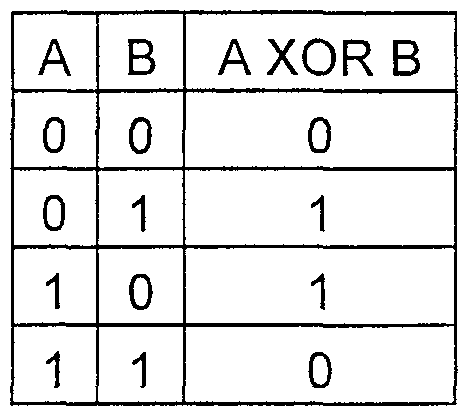
Example: 5+3=101+011=1102=610
In a polynomial form, this operation will look like
(x2+1)+(x+1)=x2+x=1102=610
Multiplication operation
To carry out the multiplication operation, it is necessary to convert numbers into a polynomial form:
5=1012=1βx2+0βx1+1βx0=x2+1
As you can see a number in a polynomial form is a polynomial whose coefficients are the values ββof bits in the binary representation of a number.
Multiply two numbers in polynomial form:
5β7=(x2+1)β(x2+x+1)=x4+x3+x2+x2+x+1=
=x4+x3+x+1=110112=2710
The result of multiplication 27 is not included in the used field. GF(23) (it consists of numbers from 0 to 7, as mentioned above). To deal with this problem, you must use the generator polynomial.
It is also assumed that x satisfies the equation f(x)=x3+x+1=0 then
Let's make the multiplication table:
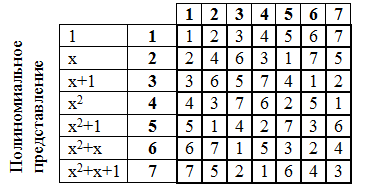
Of great importance is the table of degrees of elements of the Galois field. Exponentiation is also carried out in a polynomial form, similar to multiplication.
Example:
52=(x2+1)2=x4+x2+x2+1=x4+x2+x+x2+x+1=
=x(x3+x+1)+x2+x+1=x2+x+1=1112=710
Thus, we make a table of degrees:
The degree table is cyclical: the seventh degree corresponds to zero, which means the eighth corresponds to the first, and so on. If you wish, you can check it out.
In Galois fields, there is the concept of a primitive member - a field element whose degrees contain all non-zero field elements. It can be seen that all the elements correspond to this condition (well, except for 1, of course). However, this is not always the case.
For the fields that we consider, that is, with characteristic 2, always choose 2 as the primitive member. Given its property, any element of the field can be expressed in terms of the degree of the primitive member.
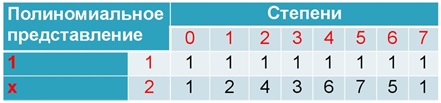
Example: 5=26,7=25
Using this property, and taking into account the cyclical nature of the table of degrees, we will try to multiply the numbers again:
5β7=26β25=2(6+5)=2(11mod7)=24=6
The result coincided with what we calculated earlier.
And now let's do the division:
6/5=24/26=2(4β6)=2((β2)mod7)=25=7
The result obtained is also true.
Well, for completeness, let's look at the exponentiation:
52=(26)2=2(6β2)=2(12mod7)=25=7
Such an approach to multiplication and division is much simpler than real operations using polynomials, and for them there is no need to store a large multiplication table, but only a row of powers of a primitive field member is sufficient.
Now back to our field GF(28)
The zero element of the field is a unit, the 1st is a deuce, each subsequent element from the 2nd to the 254th is calculated as the previous one multiplied by 2, and if the element goes beyond the field, that is, its value is greater than (28β1) then xor is done with the number 19510 , this number represents an irreducible polynomial of a field. x8+x7+x6+x+1=28+27++26+2+1=451 , we will bring this number into the box 451β256=$19 . And the 255th element is again equal to 1. Thus, we have a field containing 256 elements, that is, a complete set of bytes, and we have analyzed the basic operations that are performed in this field.
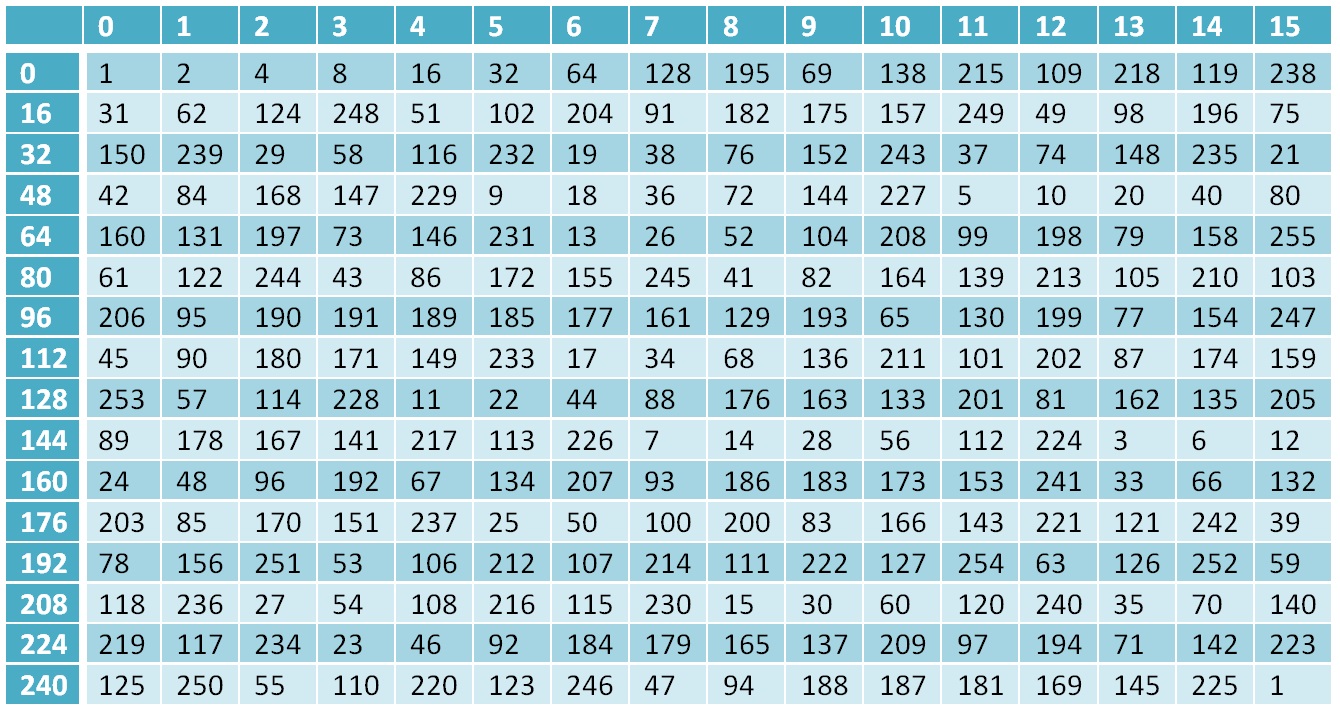
The power of two for the field GF(28)
For what it was needed - part of the calculations in the Grasshopper algorithm are performed in the Galois field, and the results of the calculations, respectively, are elements of this field.
Feistel Network
The Feistel network is a block encryption method developed by Horst Feistel in the IBM laboratory in 1971. Today, the Feistel network underlies a large number of cryptographic protocols.
The Feistel network operates with plaintext blocks:
- The block is divided into two equal parts - the left L and the right R.
- The left sub-block L is modified by the function f using the key K: X = f (L, K). Any function can be used as a function.
- The resulting subblock X is folded modulo 2 with the right subblock R, which remains unchanged: X = X + R.
- The resulting parts are interchanged and glued.
This sequence of actions is called a Feistel cell.
Figure 1. Cell Feistel
The Feistel network consists of several cells. The subblocks obtained at the output of the first cell enter the input of the second cell, the resulting subblocks from the second cell enter the input of the third cell, and so on.
Encryption algorithm
Now we are familiar with the operations used and can move on to the main topic - namely the Grasshopper cryptoalgorithm.
The basis of the algorithm is the so-called SP network - substitution-permutation network (Substitution-Permutationnetwork). The cipher based on the SP network receives a block and a key at the input and performs several alternating rounds consisting of substitution stages and permutation stages. In Grasshopper, there are nine complete rounds, each of which includes three successive operations:
- The operation of the imposition of a round key or bitwise XOR key and input data block;
- Nonlinear transformation, which is a simple replacement of one byte for another in accordance with the table;
- Linear transform. Each byte from the block is multiplied in the Galois field by one of the coefficients of the series (148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148, 1) depending on the ordinal byte numbers (a row is presented for ordinal numbers from the 15th to the 0th, as shown in the figure). The bytes are added to each other modulo 2, and all 16 bytes of the block are shifted towards the low-order bit, and the resulting number is written in place of the read byte.
The last tenth round is not complete, it includes only the first XOR operation.
Grasshopper is a block algorithm, it works with data blocks of 128 bits or 16 bytes in length. The key length is 256 bits (32 bytes).
Figure 2. Data block encryption and decryption scheme
The diagram shows the sequence of operations, where S is a nonlinear transformation, L is a linear transformation, Ki is round keys. The question immediately arises - where do the round keys come from?
Formation of round keys
Iterative (or round) keys are obtained by certain transformations based on the master key, the length of which, as we already know, is 256 bits. This process begins with splitting the master key in half, so the first pair of round keys is obtained. For the generation of each subsequent pair of round keys, eight iterations of the Feistel network are used, each iteration uses a constant, which is calculated by applying a linear transformation of the algorithm to the value of the iteration number.
The scheme of obtaining iterative (round) keys
If we recall Figure 1, then the left subblock L is the left half of the original key, the right subblock R is the right half of the original key, K is the Ci constant, f is the R sequence of operations XOR Ci, nonlinear transformation, linear transformation.
Iteration constants Ci are obtained using the L-transform of the iteration sequence number.
So, in order to encrypt a block of text, we first need to calculate 32 iteration constants, then, on the basis of the key, calculate 10 round keys, and then perform the sequence of operations shown in Figure 2.
Let's start by calculating the constants:
First constant C1=110=000000012=0116 However, all the transformations in our algorithm are performed with blocks of 16 bytes in length, so you need to add a constant to the block length, that is, add 15 null bytes to the right, we get
C1=010000000000000000000000000000
Multiply it by the row (1, 148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148) as follows:
a15=a15β148+a14β32+a13β133+a12β16+
+a11β194+a10β192+a9β1+a8β251+a7β1+a6β192+
+a5β194+a4β16+a3β133+a2β32+a1β148+a0β1
(this equality is given in Galois field operations)
Since all but the zero byte are 0, and the zero byte is multiplied by 1, we get 1 and write it to the most significant digit of the number, moving all the bytes towards the least significant bit, we get:
C1=000000000000000000000000000001
Repeat the same operations. This time a15=1 , all other bytes are 0, therefore only the first of the terms remains. a15β148=1β148=14810=9416 we get:
C1=000000000000000000000000000194
We make the third iteration, here are two nonzero terms:
a15β148+a14β32=148β148+1β32=
=10010100β10010100+00000001β00100000=
=(x7+x4+x2)β(x7+x4+x2)+1βx5=x14+x8+x4+x5=
=x6(x8+x7+x6+x+1)+x13+x12+x7+x6+x8+x4+x5=
=x5(x8+x7+x6+x+1)+x11+x5+x7+x8+x4+x5=
=x3(x8+x7+x6+x+1)+x10+x9+x3+x8+x7=
=x2(x8+x7+x6+x+1)+x2+x7=x7+x2=13210
13210=8416
According to the degree table it could be solved much easier:
148β148+1β32=245β245+25=290+25=164+32=132
C1=00000000000000000000000019484
Then everything is exactly the same, only 16 iterations for each constant
C1=0000000000000000000000019484DD
C1=0000000000000000000000019484DD10
C1=00000000000000000000019484DD10BD
C1=000000000000000000019484DD10BD27
C1=0000000000000000019484DD10BD275D
C1=00000000000000019484DD10BD275DB8
C1=000000000000019484DD10BD275DB87A
C1=0000000000019484DD10BD275DB87A48
C1=00000000019484DD10BD275DB87A486C
C1=000000019484DD10BD275DB87A486C72
C1=0000019484DD10BD275DB87A486C7276
C1=00019484DD10BD275DB87A486C7276A2
And the final constant:
C1=019484DD10BD275DB87A486C7276A2E6
The remaining constants are:
C2=02EBCB7920B94EBAB3F490D8E4EC87DC
C3=037F4FA4300469E70B8ED8B4969A25B2
C4=041555F240B19CB7A52BE3730B1BCD7B
C5=0581D12F500CBBEA1D51AB1F796D6F15
C6=06FE9E8B6008D20D16DF73ABEFF74AA7
C7=076A1A5670B5F550AEA53BC79D81E8C9
C8=082AAA2780A1FBAD895605E6163659F6
C9=09BE2EFA901CDCF0312C4D8A6440FB98
C10=0AC1615EA018B5173AA2953EF2DADE2A
C11=0B5subs8383A02424A82D8DD5280AC7C44
C12=0C3FFFD5C010671A2C7DE6951D2D948D
C13=0DAB7B08D0AD40479407AEF96F5B36E3
C14=0ED434ACE0A929A09F89764DF9C11351
C15=0F40B071F0140EFD27F33E218BB7B13F
C16=1054974EC3813599D1AC0A0F2C6CB22F
C17=11C01393D33C12C469D642635E1A1041
C18=12BF5C37E3387B2362589AD7C88035F3
C19=132BD8EAF3855C7EDA22D2BBBAF6979D
C20=1441C2BC8330A92E7487E97C27777F54
C21=15D54661938D8E73CCFDA1105501DD3A
C22=16AA09C5A389E794C77379A4C39BF888
C23=173E8D18B334C0C97F0931C8B1ED5AE6
C24=187E3D694320CE3458FA0FE93A5AEBD9
C25=19EAB9B4539DE969E0804785482C49B7
C26=1A95F6106399808EEB0E9F31DEB66C05
C27=1B0172CD7324A7D35374D75DACC0CE6B
C28=1C6B689B03915283FDD1EC9A314126A2
C29=1DFFEC46132C75DE45ABA4F6433784CC
C30=1E80A3E223281C394E257C42D5ADA17E
C31=1F14273F33953B64F65F342EA7DB0310
C32=20A8ED9C45C16AF1619B141E58D8A75E
Now we will calculate the round keys according to the scheme presented above, let's take the encryption key:
K=7766554433221100FFEEDDCCBBAA9988
EFCDAB89674523011032547698BADCFE
Then
K1=7766554433221100FFEEDDCCBBAA9988
K2=EFCDAB89674523011032547698BADCFE
K1 will be the left subblock of the Feistel network, and K2 - right.
Perform the operation K1+C1
First byte K1 equals 7716=011101112
First byte C1 equals 0116=000000012
011101112+000000012=011101102=7616
the remaining bytes are converted similarly, in the end X(K1,C1)=K1+C1 :
X(K1,C1)=76F2D199239F365D479495A0C9DC3BE6
Next, perform a nonlinear transformation S(X(K1,C1)) . It is performed according to the table:
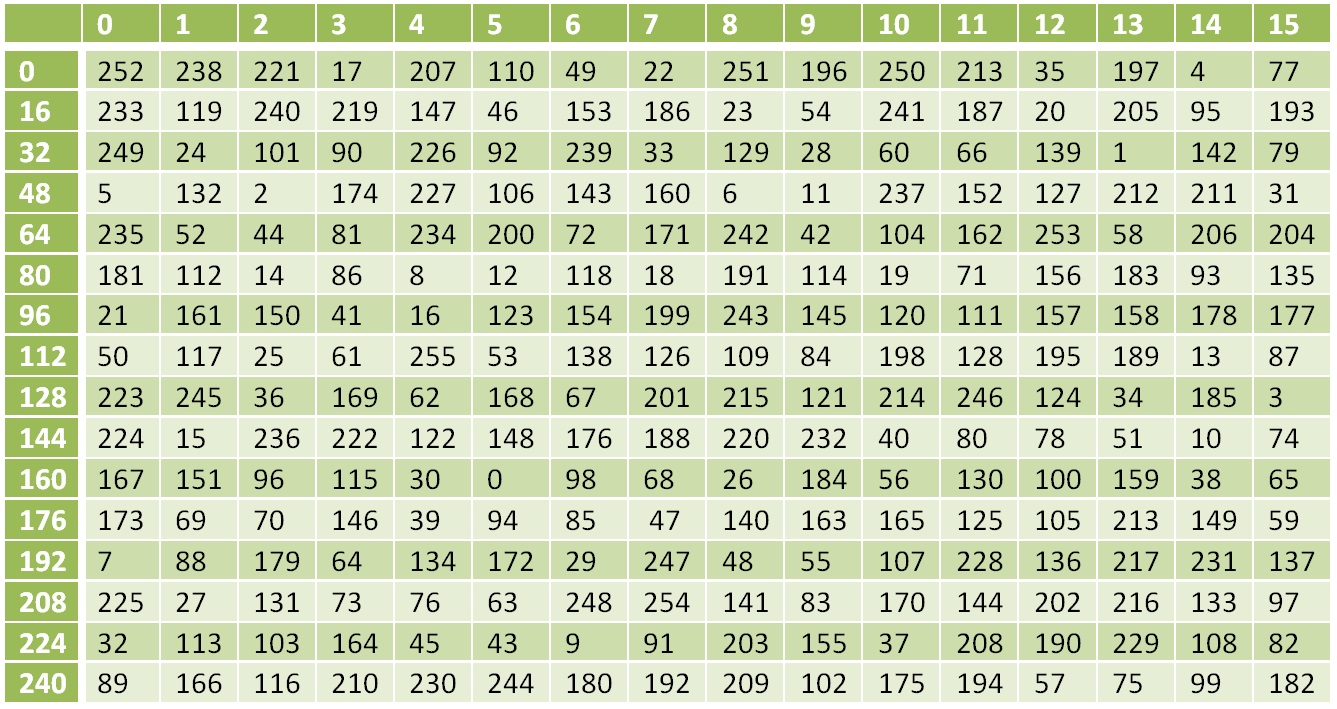
Nonlinear conversion table
The number 0 is replaced by 252, 1 by 238, 17 by 119, etc.
7616=11810
S(118)=13810=8A16
S(X(K1,C1))=8A741BE85A4A8FB7AB7A94A737CA9809
Now let's do a linear transformation. L(S(X(K1,C1))) , it was considered in detail when calculating the iteration constants, so here we give only the final result:
L(S(X(K1,C1)))=A644615E1D0757926A5DB79D9940093D
According to the Feistel cell scheme, we will execute an XOR with the right sub-block, that is, with K2 :
X(L(S(X(K1,C1))),K2)=4989CAD77A4274937A6FE3EB01FAD5C3
And the result obtained at the output of the first Feistel cell:
EFCDAB89674523011032547698BADCFE4989CAD77A4274937A6FE3EB01FAD5C3
This value is split in half and goes to the input of the second Feistel cell, where the second constant is already used. C2 . Having passed eight cells we will receive 2 following keys K3 and K4 . We run eight iterations of the Feistel network with them, we get the next pair of keys, and so on. There are eight iterations per pair of keys, since we have the first pair, there are 32 iterations in total, each with its own constant.
Remaining keys:
K3=448CC78CEF6A8D2243436915534831DB
K4=04FD9F0AC4ADEB1568ECCFE9D853453D
K5=ACF129F44692E5D3285E4AC468646457
K6=1B58DA3428E832B532645C16359407BD
K7=B198005A26275770DE45877E7540E651
K8=84F98622A2912AD73EDD9F7B0125795A
K9=17E5B6CD732FF3A52331C77853E244BB
K10=43404A8EA8BA5D755BF4BC1674DDE972
Block encryption
We calculated all the keys and now at last we can go directly to encrypting the block of text, and if you carefully read everything written above, then it will not be difficult to encrypt the text, since all the operations used and the sequence were examined in detail.
Take the plaintext block:
T=8899AABBCCDDEEFF0077665544332211
perform the sequence of operations X, S, L
X(T,K1)=FFFFFFFFFFFFFFFFFF99BB99FF99BB99
S(X(T,K1))=B6B6B6B6B6B6B6B6B6E87DE8B6E87DE8
L(S(X(T,K1)))=30081449922F4ACFA1B055E386B697E2
T1=30081449922F4ACFA1B055E386B697E2
X(T1,K2)=DFC5BFC0F56A69CEB18201951E0C4B1C
S(X(T1,K2))=61AC3B07F47891E74524EE945F23A214
L(S(X(T1,K2)))=7290C6A158426FB396D562087A495E28
T2=7290C6A158426FB396D562087A495E28
and so on, the end result will look like this:
T10=CDEDD4B9428D465A3024BCBE909D677F
Block decoding
To decrypt text, you must use the inverse operations in reverse order (see. Fig. 2).
The XOR operation is inverse to itself, the inverse of operation S is the substitution according to the following table:
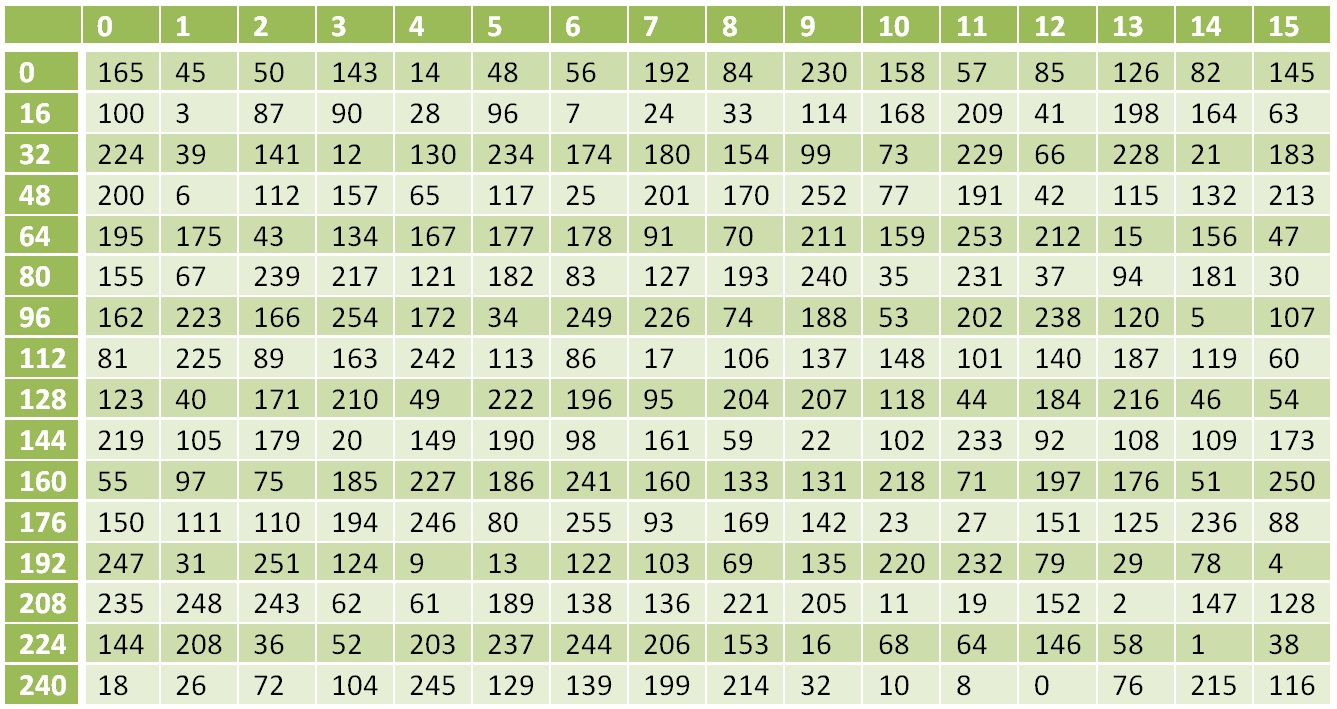
Inverse nonlinear transformation table
The inverse transform to the function L is:
a0=a15β148+a14β32+a13β133+a12β16+
+a11β194+a10β192+a9β1+a8β251+a7β1+a6β192+a5β194+
+ a 4 β 16 + a 3 β 133 + a 2 β 32 + a 1 β 148 + a 0 β 1
and a shift towards higher order. (Repeat operation 16 times)
Java implementation
First we define the necessary constants.
static final int BLOCK_SIZE = 16; // // static final byte[] Pi = { (byte) 0xFC, (byte) 0xEE, (byte) 0xDD, 0x11, (byte) 0xCF, 0x6E, 0x31, 0x16, (byte) 0xFB, (byte) 0xC4, (byte) 0xFA, (byte) 0xDA, 0x23, (byte) 0xC5, 0x04, 0x4D, (byte) 0xE9, 0x77, (byte) 0xF0, (byte) 0xDB, (byte) 0x93, 0x2E, (byte) 0x99, (byte) 0xBA, 0x17, 0x36, (byte) 0xF1, (byte) 0xBB, 0x14, (byte) 0xCD, 0x5F, (byte) 0xC1, (byte) 0xF9, 0x18, 0x65, 0x5A, (byte) 0xE2, 0x5C, (byte) 0xEF, 0x21, (byte) 0x81, 0x1C, 0x3C, 0x42, (byte) 0x8B, 0x01, (byte) 0x8E, 0x4F, 0x05, (byte) 0x84, 0x02, (byte) 0xAE, (byte) 0xE3, 0x6A, (byte) 0x8F, (byte) 0xA0, 0x06, 0x0B, (byte) 0xED, (byte) 0x98, 0x7F, (byte) 0xD4, (byte) 0xD3, 0x1F, (byte) 0xEB, 0x34, 0x2C, 0x51, (byte) 0xEA, (byte) 0xC8, 0x48, (byte) 0xAB, (byte) 0xF2, 0x2A, 0x68, (byte) 0xA2, (byte) 0xFD, 0x3A, (byte) 0xCE, (byte) 0xCC, (byte) 0xB5, 0x70, 0x0E, 0x56, 0x08, 0x0C, 0x76, 0x12, (byte) 0xBF, 0x72, 0x13, 0x47, (byte) 0x9C, (byte) 0xB7, 0x5D, (byte) 0x87, 0x15, (byte) 0xA1, (byte) 0x96, 0x29, 0x10, 0x7B, (byte) 0x9A, (byte) 0xC7, (byte) 0xF3, (byte) 0x91, 0x78, 0x6F, (byte) 0x9D, (byte) 0x9E, (byte) 0xB2, (byte) 0xB1, 0x32, 0x75, 0x19, 0x3D, (byte) 0xFF, 0x35, (byte) 0x8A, 0x7E, 0x6D, 0x54, (byte) 0xC6, (byte) 0x80, (byte) 0xC3, (byte) 0xBD, 0x0D, 0x57, (byte) 0xDF, (byte) 0xF5, 0x24, (byte) 0xA9, 0x3E, (byte) 0xA8, (byte) 0x43, (byte) 0xC9, (byte) 0xD7, 0x79, (byte) 0xD6, (byte) 0xF6, 0x7C, 0x22, (byte) 0xB9, 0x03, (byte) 0xE0, 0x0F, (byte) 0xEC, (byte) 0xDE, 0x7A, (byte) 0x94, (byte) 0xB0, (byte) 0xBC, (byte) 0xDC, (byte) 0xE8, 0x28, 0x50, 0x4E, 0x33, 0x0A, 0x4A, (byte) 0xA7, (byte) 0x97, 0x60, 0x73, 0x1E, 0x00, 0x62, 0x44, 0x1A, (byte) 0xB8, 0x38, (byte) 0x82, 0x64, (byte) 0x9F, 0x26, 0x41, (byte) 0xAD, 0x45, 0x46, (byte) 0x92, 0x27, 0x5E, 0x55, 0x2F, (byte) 0x8C, (byte) 0xA3, (byte) 0xA5, 0x7D, 0x69, (byte) 0xD5, (byte) 0x95, 0x3B, 0x07, 0x58, (byte) 0xB3, 0x40, (byte) 0x86, (byte) 0xAC, 0x1D, (byte) 0xF7, 0x30, 0x37, 0x6B, (byte) 0xE4, (byte) 0x88, (byte) 0xD9, (byte) 0xE7, (byte) 0x89, (byte) 0xE1, 0x1B, (byte) 0x83, 0x49, 0x4C, 0x3F, (byte) 0xF8, (byte) 0xFE, (byte) 0x8D, 0x53, (byte) 0xAA, (byte) 0x90, (byte) 0xCA, (byte) 0xD8, (byte) 0x85, 0x61, 0x20, 0x71, 0x67, (byte) 0xA4, 0x2D, 0x2B, 0x09, 0x5B, (byte) 0xCB, (byte) 0x9B, 0x25, (byte) 0xD0, (byte) 0xBE, (byte) 0xE5, 0x6C, 0x52, 0x59, (byte) 0xA6, 0x74, (byte) 0xD2, (byte) 0xE6, (byte) 0xF4, (byte) 0xB4, (byte) 0xC0, (byte) 0xD1, 0x66, (byte) 0xAF, (byte) 0xC2, 0x39, 0x4B, 0x63, (byte) 0xB6 }; // static final byte[] reverse_Pi = { (byte) 0xA5, 0x2D, 0x32, (byte) 0x8F, 0x0E, 0x30, 0x38, (byte) 0xC0, 0x54, (byte) 0xE6, (byte) 0x9E, 0x39, 0x55, 0x7E, 0x52, (byte) 0x91, 0x64, 0x03, 0x57, 0x5A, 0x1C, 0x60, 0x07, 0x18, 0x21, 0x72, (byte) 0xA8, (byte) 0xD1, 0x29, (byte) 0xC6, (byte) 0xA4, 0x3F, (byte) 0xE0, 0x27, (byte) 0x8D, 0x0C, (byte) 0x82, (byte) 0xEA, (byte) 0xAE, (byte) 0xB4, (byte) 0x9A, 0x63, 0x49, (byte) 0xE5, 0x42, (byte) 0xE4, 0x15, (byte) 0xB7, (byte) 0xC8, 0x06, 0x70, (byte) 0x9D, 0x41, 0x75, 0x19, (byte) 0xC9, (byte) 0xAA, (byte) 0xFC, 0x4D, (byte) 0xBF, 0x2A, 0x73, (byte) 0x84, (byte) 0xD5, (byte) 0xC3, (byte) 0xAF, 0x2B, (byte) 0x86, (byte) 0xA7, (byte) 0xB1, (byte) 0xB2, 0x5B, 0x46, (byte) 0xD3, (byte) 0x9F, (byte) 0xFD, (byte) 0xD4, 0x0F, (byte) 0x9C, 0x2F, (byte) 0x9B, 0x43, (byte) 0xEF, (byte) 0xD9, 0x79, (byte) 0xB6, 0x53, 0x7F, (byte) 0xC1, (byte) 0xF0, 0x23, (byte) 0xE7, 0x25, 0x5E, (byte) 0xB5, 0x1E, (byte) 0xA2, (byte) 0xDF, (byte) 0xA6, (byte) 0xFE, (byte) 0xAC, 0x22, (byte) 0xF9, (byte) 0xE2, 0x4A, (byte) 0xBC, 0x35, (byte) 0xCA, (byte) 0xEE, 0x78, 0x05, 0x6B, 0x51, (byte) 0xE1, 0x59, (byte) 0xA3, (byte) 0xF2, 0x71, 0x56, 0x11, 0x6A, (byte) 0x89, (byte) 0x94, 0x65, (byte) 0x8C, (byte) 0xBB, 0x77, 0x3C, 0x7B, 0x28, (byte) 0xAB, (byte) 0xD2, 0x31, (byte) 0xDE, (byte) 0xC4, 0x5F, (byte) 0xCC, (byte) 0xCF, 0x76, 0x2C, (byte) 0xB8, (byte) 0xD8, 0x2E, 0x36, (byte) 0xDB, 0x69, (byte) 0xB3, 0x14, (byte) 0x95, (byte) 0xBE, 0x62, (byte) 0xA1, 0x3B, 0x16, 0x66, (byte) 0xE9, 0x5C, 0x6C, 0x6D, (byte) 0xAD, 0x37, 0x61, 0x4B, (byte) 0xB9, (byte) 0xE3, (byte) 0xBA, (byte) 0xF1, (byte) 0xA0, (byte) 0x85, (byte) 0x83, (byte) 0xDA, 0x47, (byte) 0xC5, (byte) 0xB0, 0x33, (byte) 0xFA, (byte) 0x96, 0x6F, 0x6E, (byte) 0xC2, (byte) 0xF6, 0x50, (byte) 0xFF, 0x5D, (byte) 0xA9, (byte) 0x8E, 0x17, 0x1B, (byte) 0x97, 0x7D, (byte) 0xEC, 0x58, (byte) 0xF7, 0x1F, (byte) 0xFB, 0x7C, 0x09, 0x0D, 0x7A, 0x67, 0x45, (byte) 0x87, (byte) 0xDC, (byte) 0xE8, 0x4F, 0x1D, 0x4E, 0x04, (byte) 0xEB, (byte) 0xF8, (byte) 0xF3, 0x3E, 0x3D, (byte) 0xBD, (byte) 0x8A, (byte) 0x88, (byte) 0xDD, (byte) 0xCD, 0x0B, 0x13, (byte) 0x98, 0x02, (byte) 0x93, (byte) 0x80, (byte) 0x90, (byte) 0xD0, 0x24, 0x34, (byte) 0xCB, (byte) 0xED, (byte) 0xF4, (byte) 0xCE, (byte) 0x99, 0x10, 0x44, 0x40, (byte) 0x92, 0x3A, 0x01, 0x26, 0x12, 0x1A, 0x48, 0x68, (byte) 0xF5, (byte) 0x81, (byte) 0x8B, (byte) 0xC7, (byte) 0xD6, 0x20, 0x0A, 0x08, 0x00, 0x4C, (byte) 0xD7, 0x74 }; // static final byte[] l_vec = { 1, (byte) 148, 32, (byte) 133, 16, (byte) 194, (byte) 192, 1, (byte) 251, 1, (byte) 192, (byte) 194, 16, (byte) 133, 32, (byte) 148 }; // static byte[][] iter_C = new byte[32][16]; // static byte[][] iter_key = new byte[10][64]; Let's create all the main functions:
// X static private byte[] GOST_Kuz_X(byte[] a, byte[] b) { int i; byte[] c = new byte[BLOCK_SIZE]; for (i = 0; i < BLOCK_SIZE; i++) c[i] = (byte) (a[i] ^ b[i]); return c; } // S static private byte[] GOST_Kuz_S(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; for (i = 0; i < BLOCK_SIZE; i++) { int data = in_data[i]; if(data < 0) { data = data + 256; } out_data[i] = Pi[data]; } return out_data; } To implement the function L, we need several auxiliary functions, one for calculating the multiplication of numbers in the Galois field, and one for the shift.
// static private byte GOST_Kuz_GF_mul(byte a, byte b) { byte c = 0; byte hi_bit; int i; for (i = 0; i < 8; i++) { if ((b & 1) == 1) c ^= a; hi_bit = (byte) (a & 0x80); a <<= 1; if (hi_bit < 0) a ^= 0xc3; // x^8+x^7+x^6+x+1 b >>= 1; } return c; } // R , L- static private byte[] GOST_Kuz_R(byte[] state) { int i; byte a_15 = 0; byte[] internal = new byte[16]; for (i = 15; i >= 0; i--) { if(i == 0) internal[15] = state[i]; else internal[i - 1] = state[i]; a_15 ^= GOST_Kuz_GF_mul(state[i], l_vec[i]); } internal[15] = a_15; return internal; } static private byte[] GOST_Kuz_L(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; byte[] internal = in_data; for (i = 0; i < 16; i++) { internal = GOST_Kuz_R(internal); } out_data = internal; return out_data; } Reverse functions:
// S^(-1) static private byte[] GOST_Kuz_reverse_S(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; for (i = 0; i < BLOCK_SIZE; i++) { int data = in_data[i]; if(data < 0) { data = data + 256; } out_data[i] = reverse_Pi[data]; } return out_data; } static private byte[] GOST_Kuz_reverse_R(byte[] state) { int i; byte a_0; a_0 = state[15]; byte[] internal = new byte[16]; for (i = 1; i < 16; i++) { internal[i] = state[i - 1]; a_0 ^= GOST_Kuz_GF_mul(internal[i], l_vec[i]); } internal[0] = a_0; return internal; } static private byte[] GOST_Kuz_reverse_L(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; byte[] internal; internal = in_data; for (i = 0; i < 16; i++) internal = GOST_Kuz_reverse_R(internal); out_data = internal; return out_data; } // static private void GOST_Kuz_Get_C() { int i; byte[][] iter_num = new byte[32][16]; for (i = 0; i < 32; i++) { for(int j = 0; j < BLOCK_SIZE; j++) iter_num[i][j] = 0; iter_num[i][0] = (byte) (i+1); } for (i = 0; i < 32; i++) { iter_C[i] = GOST_Kuz_L(iter_num[i]); } } // , static private byte[][] GOST_Kuz_F(byte[] in_key_1, byte[] in_key_2, byte[] iter_const) { byte[] internal; byte[] out_key_2 = in_key_1; internal = GOST_Kuz_X(in_key_1, iter_const); internal = GOST_Kuz_S(internal); internal = GOST_Kuz_L(internal); byte[] out_key_1 = GOST_Kuz_X(internal, in_key_2); byte key[][] = new byte[2][]; key[0] = out_key_1; key[1] = out_key_2; return key; } // public void GOST_Kuz_Expand_Key(byte[] key_1, byte[] key_2) { int i; byte[][] iter12 = new byte[2][]; byte[][] iter34 = new byte[2][]; GOST_Kuz_Get_C(); iter_key[0] = key_1; iter_key[1] = key_2; iter12[0] = key_1; iter12[1] = key_2; for (i = 0; i < 4; i++) { iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[0 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[1 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[2 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[3 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[4 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[5 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[6 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[7 + 8 * i]); iter_key[2 * i + 2] = iter12[0]; iter_key[2 * i + 3] = iter12[1]; } } // public byte[] GOST_Kuz_Encript(byte[] blk) { int i; byte[] out_blk = new byte[BLOCK_SIZE]; out_blk = blk; for(i = 0; i < 9; i++) { out_blk = GOST_Kuz_X(iter_key[i], out_blk); out_blk = GOST_Kuz_S(out_blk); out_blk = GOST_Kuz_L(out_blk); } out_blk = GOST_Kuz_X(out_blk, iter_key[9]); return out_blk; } // public byte[] GOST_Kuz_Decript(byte[] blk) { int i; byte[] out_blk = new byte[BLOCK_SIZE]; out_blk = blk; out_blk = GOST_Kuz_X(out_blk, iter_key[9]); for(i = 8; i >= 0; i--) { out_blk = GOST_Kuz_reverse_L(out_blk); out_blk = GOST_Kuz_reverse_S(out_blk); out_blk = GOST_Kuz_X(iter_key[i], out_blk); } return out_blk; } Well, the main function
static byte[] key_1 = {0x77, 0x66, 0x55, 0x44, 0x33, 0x22, 0x11, 0x00, (byte) 0xff, (byte) 0xee, (byte) 0xdd, (byte) 0xcc, (byte) 0xbb, (byte) 0xaa, (byte) 0x99, (byte) 0x88}; static byte[] key_2 = {(byte) 0xef, (byte) 0xcd, (byte) 0xab, (byte) 0x89, 0x67, 0x45, 0x23, 0x01, 0x10, 0x32, 0x54, 0x76, (byte) 0x98, (byte) 0xba, (byte) 0xdc, (byte) 0xfe}; static byte[] blk = DatatypeConverter.parseHexBinary("8899aabbccddeeff0077665544332211"); public static void main(String[] args) { GOST_Kuz_Expand_Key(key_1, key_2); byte[] encriptBlok = GOST_Kuz_Encript(blk); System.out.println(DatatypeConverter.printHexBinary(encriptBlok)); byte[] decriptBlok = GOST_Kuz_Decript(encriptBlok); System.out.println(DatatypeConverter.printHexBinary(decriptBlok)); } We have learned to encrypt a data block in order to encrypt text whose length is greater than the block length, there are several modes described in the standard - GOST 34.13-2015:
- simple replacement mode (Electronic Codebook, ECB);
- gamma mode (Counter, CTR);
- Gamma mode with output feedback (Output Feedback, OFB);
- Cipher Block Chaining, CBC;
- Ciphertext gamming mode (Cipher Feedback, CFB);
- mode of generation of imitovstavki (Message Authentication Code, MAC).
In all modes, the text length must always be a multiple of the block length, therefore the text is always padded to the right with one single bit and zeros to the block length.
The simplest mode is the simple replacement mode. In this mode, the text is divided into blocks, then each block is encrypted separately from the others, then the blocks of the encrypted text are glued together and we get an encrypted message. This mode is both the easiest and most vulnerable and almost never used in practice.
The remaining modes will probably be discussed in detail later.
Source: https://habr.com/ru/post/459004/
All Articles