Secrets of working with a cloth in the game Alan Wake

[Remedy animation programmer Henrik Enquist told how his team created a convincing simulation of a tweed jacket for the protagonist of the horror-thriller Alan Wake game.]
The main character of our action-thriller is Alan Wake, a writer who has fallen into a nightmare, where he is forced to fight dark forces and solve the riddle of his wife's disappearance. He is not a well-trained action movie hero, but an ordinary person.
To emphasize the character’s character, our art director wanted to dress him in an old tweed jacket with patches on the elbows. The game takes place in the entourage of the real world, therefore, unlike the fantasy game or space shooter, the characters are limited in the tools used. This means that the clothes of our characters become much more important.
')
To convey the illusion of the atmosphere of a thriller, Alan Wake's jacket must be as believable as possible. The jacket should develop in the wind and add auxiliary movements to the character when moving through the forest. As a programmer, I immediately started thinking about using fabric simulation.
Fabric simulation was used in a variety of games before us, but often the methods used there gave a feeling of silk or rubber - materials that are unsuitable for us. Only very recently began to appear very good systems of simulation of tissues of third-party companies, but at the time when we needed a stable solution, such tools did not exist yet, or they did not meet our needs.
In this article I will talk about the problems that we have encountered, and the solutions for creating our own fabric simulation.
Rig jacket
The jacket was modeled along with the rest of the character as a regular skinning mesh. The bones that drive the mesh of the jacket are a separate layer on top of the normal skeleton. The sleeves of the jacket use the usual pattern for the shoulder and forearm. Both shoulders and forearms are divided into one main bone and one bend bone. The upper part of the jacket is controlled by the look-at constraints, and the lower part is controlled by the Verlet simulation.

Figure 1. Rig jacket over a regular game skeleton.
Jacket Upper
Jacket bones have a top-down hierarchy (the lower ones are child elements of the upper ones), so when the upper bones move, the lower bones follow them. We were tempted to make the lower bones affiliated directly to the rib cage, but this would cause a loss of movement, especially vertical movement, when the character lifts his shoulders.
At the top of the jacket, we imitate the movement of the overlays on the shoulders, moving the bones of the shoulder glands using look-at constraints towards the bones of the shoulders. Thanks to this, the overlays follow the shoulder, and when raising a hand, the overlay raises the rest of the bones, as in a real jacket.
What does the look-at costraint constraint look like?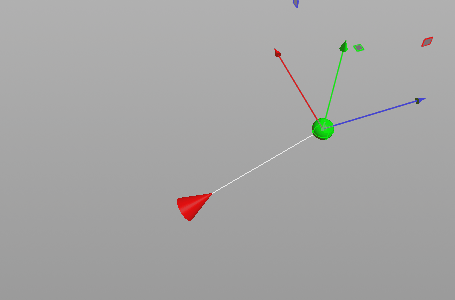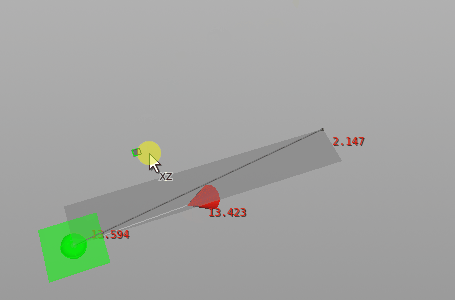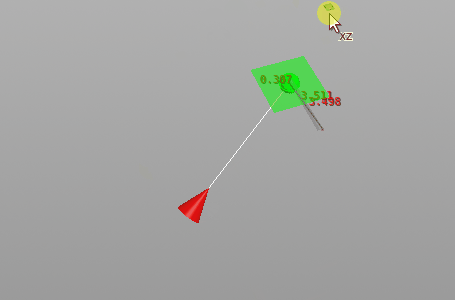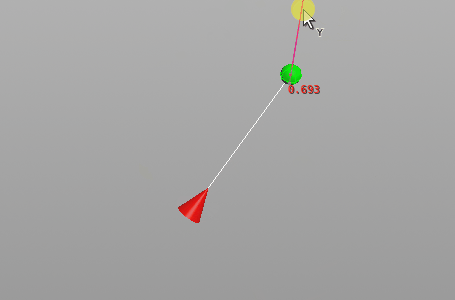
Costraint look-at applied to red cone

Costraint look-at applied to red cone
The next bone in the chain is the layer between the top of the jacket and the simulated bottom. These bones are controlled by look-at constraints directly down to compensate for the rotation that is created by the shoulders. We also added position constraints between the left and right bones to compensate for the stretching that occurs when the overlays on the shoulders move.

Figure 2. The movement of the bones when raising a hand by a character.
This could be quite enough for the implementation of restrictions in the animation exporter and baking the results into the animation data, but we still wanted to control the bones in the game engine in real time.
Because of this, we could save a few bytes in these animations, and also easily transfer animations between characters, regardless of whether there are jackets on them. In addition, the upper arm movements generated by game inverse kinematics (for example, at the time of aiming) would be correctly applied when real-time constraints were resolved.
Bottom of the jacket
Solving the problem with the upper part of the jacket, we went to the simulation of the lower part. Most gaming fabric simulations use a one-to-one binding between the vertices in the fabric simulation and the rendered mesh vertices.
We wanted to preserve the accuracy of the jacket mesh so that it is not hampered by any restrictions determined by the programmer. For example, if we decided to use the same mesh as for rendering, then the silhouette of the pockets and the front of the jacket would be lost.
We could use normal maps to give a jacket a volume, but we felt that this would not be enough. We wanted our artists to model the jacket the way they wanted it, and then let them use normal maps to add folds or other details instead of compensating for lost geometry.
We came to this decision: create a low-resolution mesh fabric to simulate a jacket, and then tie it to the bones of the skeleton used to control the skinning mesh.


Figure 3. Comparison of the silhouettes of our jacket and fabric, having the same vertex with the simulation.
Werle Physics
First we look at Werle's physics, and then we learn how to create a matching simulation of bones. Currently, Werle's physics is the standard solution for tissue simulation in games. If you are unfamiliar with Verlet's technique, then I recommend to start reading one of these articles on Gamasutra: Devil in the Blue Faceted Dress: Real Time Cloth Animation or Advanced Character Physics .

Figure 4. A 4x4 vertex grid and constraints for one of the vertices.
For the rest, I will briefly repeat the principle of operation. Figure 4 shows a mesh of fabric and spring constraints for one of its vertices. As can be seen from the figure, each vertex of the mesh is connected to all adjacent vertices, as well as to their neighbors.
Restrictions from immediate neighbors are called stretch constraints and are indicated by blue. Long constraints indicated by red are called shear / bend constraints.
It is important to keep these restrictions in two groups, because later we will resolve them with different parameters. Note that in our jacket the top row of fabric points is tied with skinning to the character and will not be controlled by the simulation.
The presence of a mesh in the form of a grid is not a mandatory requirement of the algorithm itself, however, to simulate a fabric with such a topology, it is easiest to work. The foundation of fabric simulation consists of two parts. The first part is the Verlet integration, in which we calculate the velocity for each vertex and apply it to the position.
Vector3 vVelocity = vertex.vCurrentPosition - vertex.vPreviousPosition; vertex.vPreviousPosition = vertex.vCurrentPosition; vertex.vCurrentPosition += vVelocity * ( 1.0f - fDampingFactor ) + vAcceleration * fDeltaTime * fDeltaTime; In our project,
vAcceleration was vAcceleration sum of gravitational force and wind. Attenuation was used both to adjust the appearance of the jacket and to stabilize the simulation. The high attenuation fDampingFactor gives the jacket a feeling of a very light fabric that fDampingFactor down slowly and smoothly, and a small attenuation rate makes the jacket harder, causing it to sway / hesitate after movement longer.The second part of the algorithm is the resolution of spring constants (spring constraints) (this process is called relaxation). For each constraint, we attract or push vertices apart so that they satisfy their original lengths. Here is a snippet of code in a readable form.
Vector3 vDelta = constraint.m_vertex1.m_vCurPos - constraint.m_vertex0.m_vCurPos; float fLength = vDelta.length(); vDelta.normalize(); Vector3 vOffset = vDelta * ( fLength - constraint.m_fRestLength ); constraint.m_vertex0.m_vCurrentPosition += vOffset / 2.0f; constraint.m_vertex1.m_vCurrentPosition -= vOffset / 2.0f; Stretch restrictions keep the tops of the fabric together, and tilt / bend restrictions help keep the fabric in shape. As you can see, with the ideal solution of this system, the fabric will move too hard. That is why, before we allow new positions, we add a coefficient to the slope / bend constraints.
vOffset *= fStiffness; constraint.m_vertex0.m_vCurrentPosition += vOffset / 2.0f; constraint.m_vertex1.m_vCurrentPosition -= vOffset / 2.0f; At a stiffness coefficient of 1.0, the fabric will be non-ductile, and at 0.0, the fabric will flex without any restrictions.
Fixed time step
You must have noticed that Verlet integration assumes that the previous time step was exactly the same as the current one; otherwise, the calculated speed will be incorrect. When using Werle integration, it is possible to do with variable time steps, but the resolution of constraints is very sensitive to changes in the time step.
Since the solver solves the problem, iteratively bypassing the constraints, they can never be solved ideally. In the game, this inaccuracy will manifest itself in the form of stretching, and the shorter the time step, the less stretching the player will see.
Ultimately, this will be a compromise between accuracy and the amount of processor time you can spend on clothing. If the time step is not constant, then the stretching of the clothes will vary, and we will introduce unwanted vibrations into the system. More importantly, the time step will affect the stiffness index and other parameters of the fabric: the shorter the time interval, the tighter the fabric will be, even when using the same stiffness coefficient.
In practice, this means that before you begin to customize the appearance of clothes using the parameters of the fabric, you will have to decide on a fixed time step. I know that there are games in which a variable time step is used for physics, but my personal experience tells me that life becomes much easier when the time step for physics and game logic is fixed.
Hood
Before we get into the details of the fabric simulation, let's take a quick look at how the hood is simulated. To skin the top of the hood mesh, we used the extra bone. We created a pendulum from the center of the bone to the position behind the hood. The end of the pendulum is one particle, controlled by Werle's physics. Then, using the look-at constraint, the bone is directed towards the pendulum.

Figure 5. Hood and pendulum.
Creating Bone Matrices
The hood gives us a hint on what to do next with the bottom of the jacket. We will use the vertex positions in the simulated mesh to calculate the bone transformations.
The first thing we do is match the bones so that the hinge of each bone corresponds to the top of the simulated mesh. Due to this, the assignment of the part of the matrix relating to the displacement will be a trivial process.
Then we need to calculate the 3x3 rotation matrix. Each row (or column, depending on the configuration of the matrix) is given by the x, y, and z axes of the bone.
We specify the x axis of the bone as the direction from the base vertex to the next one under it. Then the y axis is defined by a vector from the top to the left to the top to the right.

Figure 6. Bones attached to a mesh mesh.
In Figure 6, the x axis is shown in red, and the y axis in green. The z axis is then calculated as the vector product of these vectors. In the end, we also orthonorse the matrix to get rid of the distortion in the displacement data.
As you can see, in the vertical direction we use each line of the mesh of the cloth (except for the last one) to adjust the bones, but in the horizontal one only every second column is used. Besides the fact that it gives the artistic advantages described above, this method is also quite fast. Because of this, traditional skinning techniques can be applied on the GPU side to render the mesh, because otherwise we would have to update the huge dynamic vertex buffer.
The fabric mesh can have a fairly low resolution, which reduces the load on the CPU. The only additional cost to our solution is to convert a low resolution simulation into a high resolution mesh, but in our scheme these costs will be negligible compared to the rest of the simulation.
Collisions
To solve the problem of cutting the tissue with the feet and the body, we use collision detection between the ellipsoid and the particle. Figure 7 shows the ellipsoids needed to allow the character model to truncate a jacket.

Figure 7. Ellipsoid system for the Wake model.
Recognition of collisions of ellipsoids with particles is performed very quickly. Collisions can be solved by transforming the space in which the ellipsoid and the particle exist, due to which the ellipsoid turns into a sphere. Then you can perform a quick test of collisions of the sphere and particles.
In practice, this is accompanied by the creation of an inverse transform based on the values of the length, width and height of the ellipsoid with its application to the position of the particle. The only problem here is that the collision normal, which we get after converting back to the original coordinate system, is distorted.
We decided that we could accept a slight inaccuracy in calculating the direction of the collision. In cases where a strongly stretched ellipsoid could cause incorrect reactions, we divided it into two more homogeneous ones.
Maximum distance to particle
Another problem that had to be solved was the stability of the jacket. The fabric with the rapid movement could cause the creation of nodes or be on the other side of the volume of collisions and pass through the body. We solved this problem by setting a safe distance for each vertex of the simulated tissue.
For each vertex, the original resting position is attached by skinning to the nearest bone and we use it as a reference point. If the simulation exceeds the threshold value, then we simply move the vertex closer to the reference point. In our scheme, we allowed the vertices below to move a greater distance than the vertices are closer to the shoulder glands.
The maximum distance that we can allow the vertices to move is about 40 cm, when this value is exceeded, rare cases of knots and truncation begin to manifest themselves. We also tried to use other techniques, for example, the plane of collisions, but the maximum distance method turned out to be the best. It was fast, easy to set up, and provided the greatest freedom of movement before noticeable errors began to appear in the fabric.
More tweed, less rubber
So far we have managed to find good ways to achieve our goals. Our artist modeled the jacket as he liked; for animating the jacket there was no need for an animator, because everything was simulated in the game, and the processor was pleased that we had enough resources for other in-game calculations. But we were worried about one thing - the fabric looked like rubber.
Struggling with stretching
First, we need to get rid of stretching. As I said above, the phenomenon of stretching is caused by errors that appear due to the iterative nature of the algorithm. This is a popular research topic and you can find many ways to solve this problem.
Unfortunately, all the available solutions would force us to allocate much more scarce CPU resources to fabric calculations. Therefore, we solved the problem of stretching, adding to the simulation of the fabric the last stage, at which the so-called “hard constraints” are applied.
We have made tight restrictions with stretch restrictions (all of them are directed vertically). These restrictions were sorted from top to bottom so that the restrictions near the shoulders were resolved to the restrictions near the legs.
Since we are iterating constraints from above, we know that the upper vertex in the pair has already been solved and does not cause any stretching, so we need only move the lower vertex towards the upper one. Because of this, we can be sure that after a single iteration, the length from top to bottom will be exactly the same as the length in the resting position.
Vector3 vDelta = constraint.m_vertexTop.m_vCurPos - constraint.m_vertexDown.m_vCurPos; float fLength = vDelta.length(); vDelta.normalize(); Vector3 vOffset = vDelta * ( fLength - constraint.m_fRestLength ); constraint.m_vertexDown.m_vCurrentPosition += vOffset; 
Figure 8. Hard constraints.
As you can see, we do not take into account the horizontal stretching of the jacket. It is impossible to apply strict restrictions to the horizontal direction, because the vertex will be resolved twice, that is, we will lose the results of the vertical calculation step and the length of the fabric alone will not be preserved.
However, we noticed that in the case of a jacket, horizontal stretching actually remains imperceptible to the human eye, and because of the vertical stretching, the jacket looks very bad. This decision was quite good.
Jacket edges
Secondly, we wanted the edges of the jacket to move a little more than the rest of it. For example, if you run in an open jacket, you will notice that the air resistance has a greater effect on the edges of the jacket than on the central part. This is because your body shields the rest of the jacket from the wind.
Edges can be easily found by the number of restrictions attached to them. Any vertex with less than four stretch constraints is a boundary. Therefore, we can mark these vertices and simulate them with other parameters.
- Reduced attenuation.
- Global wind has a greater impact.
- Movement in world space has a greater impact (for more details on movement in world space, see below).
- Permissible maximum safety distance is higher.
Due to this, the internal frequency of the edges will be different from the rest of the jacket. Now the entire jacket does not respond to impulses as a large pendulum, and only edges add to the movement a beautiful auxiliary movement.

Figure 9. Vertex edges.
Movement in world space and in local space
Then we noticed that when the character moves, movement in the global space has a rather large effect on the simulation, while small local body turns or movements of the shoulder girdle go unnoticed.
In traditional fabric simulation, the vertex positions are simulated in global space. Someone may say that it is right to pretend fabric so, but it feels unnatural. Therefore, we simulated a jacket on the characters in the local space and separately added a small movement in the global space. We have noticed that the results we need are obtained with 100% local animation of the skeleton with 10-30% of movement in global space.
Friction
And finally, we wanted to exaggerate the contrast between the jacket in slow and fast motion. We wanted the jacket to be relatively motionless when walking, and when Alan jumps or dodges, the movement should be more alive.
We thought that when the jacket touches the body, it should move less because of friction between the jacket and the shirt, and when the jacket rises, it should move harder because nothing restricts it. We imitated this by applying a higher attenuation value to each vertex touching the ellipsoid. Because of this, the tops touching the body will appear a bit sticky, creating enough contrast between the jacket in a normal situation and in fast motion.
Conclusion and further work
The first incarnation of a fabric simulation was quite simple to implement: we just searched for the word “fabric” in the game development literature and applied the algorithms found. The second stage, at which we tried to achieve a convincing sensation of a tweed jacket, required the study of scientific articles, a lot of trial and error, and even the removal of part of the code.
Of course, you can always improve something. For example, using low-resolution simulation and linking it to a high-resolution mesh complicates the problem of all truncations. We didn’t have enough time for other small details: for example, maps of folds at the places of jacket folds or implementation of correct jacket interaction with a tornado.
In the end, our efforts paid off - our fabric is very different from the fabric simulation in other games. It looks much more like tweed than silk or rubber. In addition, our system was very flexible and allowed to simulate other fabrics, such as the down jacket of Barry Wheeler and the veil of the old lady. It seems that by adjusting the parameters you can achieve a simulation and other types of tissue.

Figure 10. Tweed jacket.
Source: https://habr.com/ru/post/458486/
All Articles