Manual segmentation of the lungs takes about 10 minutes and requires some dexterity to get the same high-quality result as with automatic segmentation. Automatic segmentation takes about 15 seconds.

I assumed that without a neural network it would be possible to get an accuracy of no more than 70%. I also assumed that morphological operations are only the preparation of an image for more complex algorithms. But as a result of processing those, although few 40 samples of tomographic data on hand, the algorithm identified the lungs without errors, and after the test in the first five cases, the algorithm did not undergo significant changes and from the first application correctly worked on the remaining 35 studies without change settings.

Also, neural networks have a minus - for their training, we need hundreds of training samples of the lungs, which will have to be marked out manually.

Content

• The structure of the respiratory system
• Hounsfield scale
• Mathematical morphology
• Lee algorithm and RLE compression
• Threshold conversion base volume
• Cut off outside air
• The allocation of the maximum volume of the object
• Closing the vessels inside the lungs
• Algorithm segmentation of the respiratory organs
• The implementation of the algorithm in the MATLAB environment
• Conclusion

The structure of the respiratory system

The respiratory system includes the airways and lungs. Allocate upper and lower respiratory tract. The point of separation between the lower and upper respiratory tract is the intersection of the food and respiratory channels. All that is higher than the larynx is the upper section, and the rest is the lower one.

We list the respiratory organs:
Nasal cavity : - nose, maxillary sinuses, etc.
The pharynx is a channel through which food and air travels.
Larynx - is responsible for the formation of voices. Located at the level of the cervical vertebrae C4-C6.
The trachea is a tube connecting the larynx and bronchi.
The bronchi are the respiratory channels, the main part of which is located inside the lungs.
The lungs are the main respiratory organ.

Hounsfield scale

Godfrey Hounsfield is a British electrical engineer who, together with American theorist Allan Cormac, developed computed tomography, for which he won the Nobel Prize in 1979.

The Hounsfield scale is the quantitative x-ray density scale, which is measured in Hounsfield units, denoted by HU.

X-ray density is calculated on the basis of the attenuation coefficient of the substance, that is, the degree of reduction of the radiation power during its passage through this substance.

X-ray density is calculated by the formula:

$$$$ display $$ {μ_ {X} -μ_ {water} \ over μ_ {water} -μ_ {air}} \ times 1000 $$ display $$

Where $$$μ_X, μ_ {water}, μ_ {air}$- linear attenuation coefficients for the measured substance, water and air.

X-ray density is negative because zero x-ray density corresponds to water. This means that all substances through which X-ray waves pass with a smaller decrease in radiation power than through water (for example, lung tissue, air) will have a negative X-ray density.

The following are the approximate x-ray densities for various tissues:

• Air: -1000 HU.
• Respiratory organs: from -950 to -300 HU.
• Blood (without contrasting vessels): from 0 to 100 HU.
• Bones: 100 to 1000 HU.

Wikipedia links: Hounsfield scale , Godfrey Hounsfield , attenuation coefficient .

Mathematical morphology

The main place among the algorithms chosen in this article is occupied by morphological operations.

In the field of computer vision, morphological operations are called a group of algorithms for the transformation of the shape of objects. Most often, morphological operations are applied to binarized images where units correspond to object voxels, and zeros correspond to emptiness.

The main morphological operations include:

Morphological dilatation (dilation, expansion) - adding new voxels to all marginal voxels of objects. That is, a passage with a core with a given shape (ball, cube, cross, etc.) is made on all boundary voxels. This operation is often used to connect multiple nearby objects into a single object.

Morphological erosion (erosion, erosion) - the destruction of all voxels lying on the border of objects. This operation is reverse dilatation. This operation is useful for removing noise in the form of many small objects interconnected. However, this method of noise removal should be used only if the segmented object has a thickness much larger than the radius of erosion.

Morphological closing (closing) is dilatation with subsequent erosion. It is used to close holes inside objects and to merge nearby objects.

Morphological opening (opening) is erosion with subsequent dilatation. It is used to remove small noise objects and to divide objects into several objects.

Lee algorithm and RLE compression

To select objects in binarized voxel volume, the Lie algorithm is used. This algorithm was originally invented to find the shortest path. But we use it to select and move objects from one three-dimensional array of voxels to another. Its essence consists in parallel movement in all possible directions from the starting point. For a three-dimensional case, 26 or 6 directions of motion from a given voxel are possible (if the voxel is not located at the edge of the image).

To optimize the performance, the run-length encoding algorithm was applied. Its essence lies in the fact that the sequence of ones and zeros is replaced by a digit equal to the number of elements in the sequence. For example, the string “00110111” can be replaced by: “2; 2; 1; 3”. This reduces the number of memory accesses.

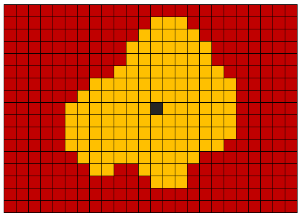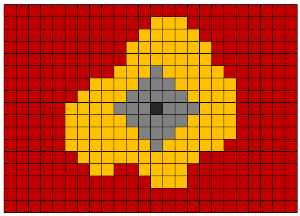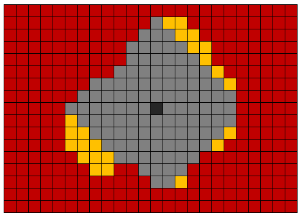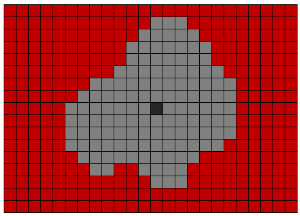
References to Wikipedia: Lee algorithm, RLE algorithm .

Threshold conversion base volume

With the help of the tomograph obtained data on x-ray density at each point in space. Air voxels have an x-ray density between -1100 and -900 HU, and voxels of the respiratory organs between -900 and -300 HU. Therefore, we can remove all excess voxels with X-ray density greater than -300 HU. As a result, we obtain a binarized voxel volume containing only the respiratory organs and air.

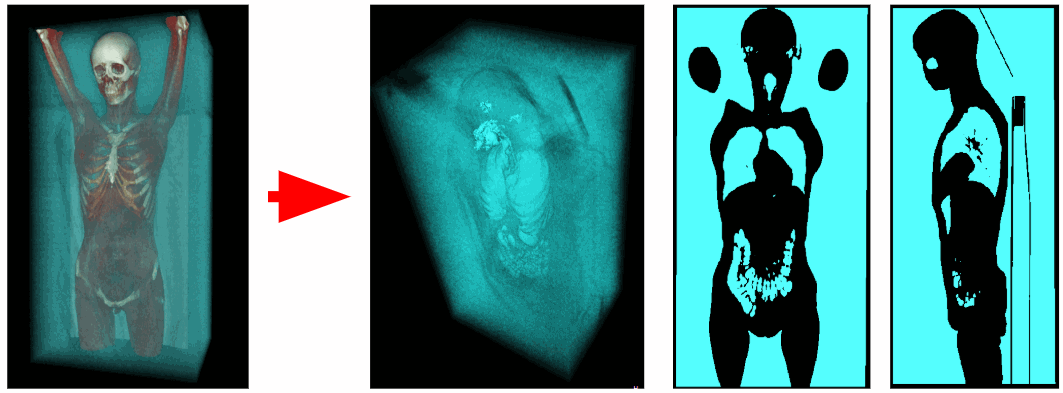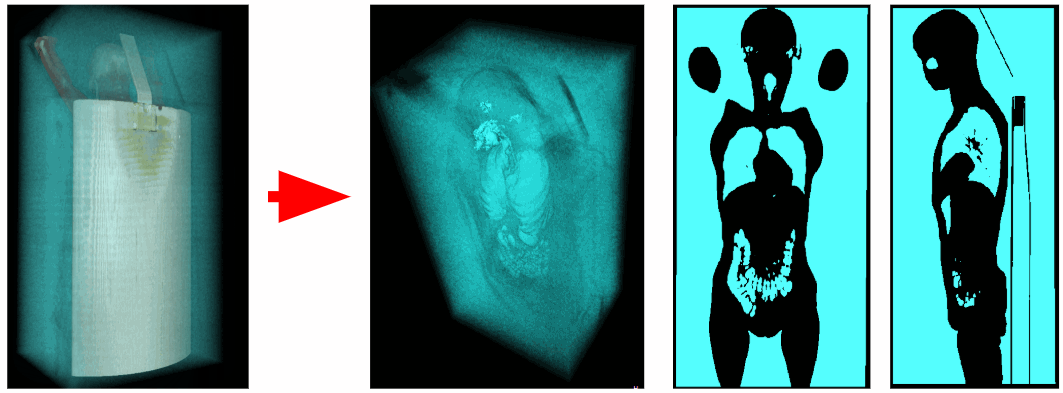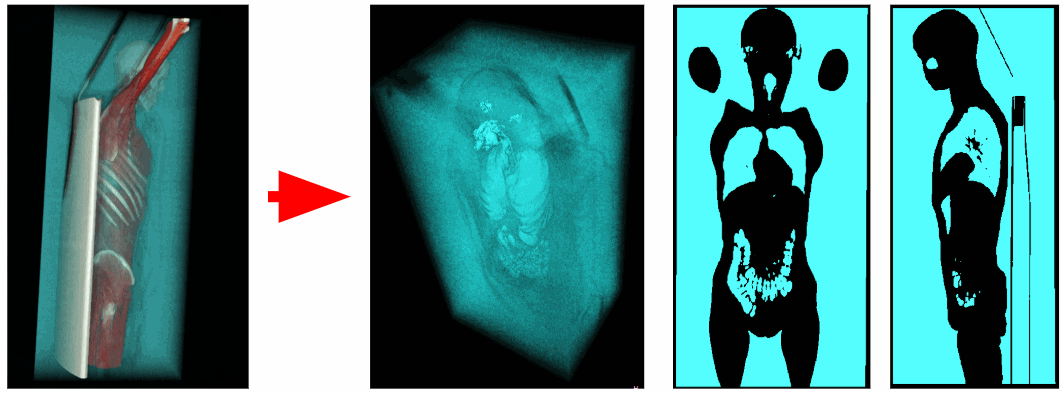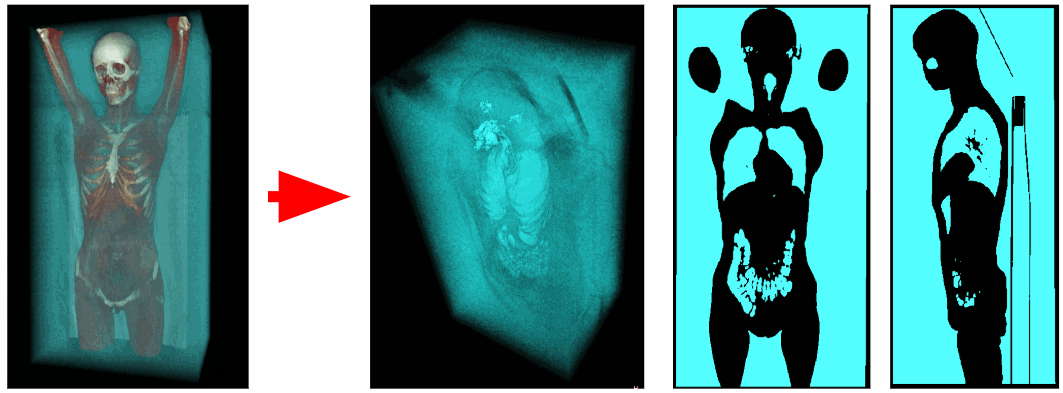
Cut off outside air

To separate the internal air of the body, we delete all objects that are adjacent to the corners of the voxel scene. So get rid of the outside air.

However, not all cases will remove the air inside the table of the scanner, as it may not have a connection with the corners of the scene.

Therefore, we will scan not only the corners, but also all the voxels lying on any of the edge planes of the scene. But as a result, for some reason, the lungs themselves also retired. It turns out that the trachea also had a connection with the upper plane of the stage.

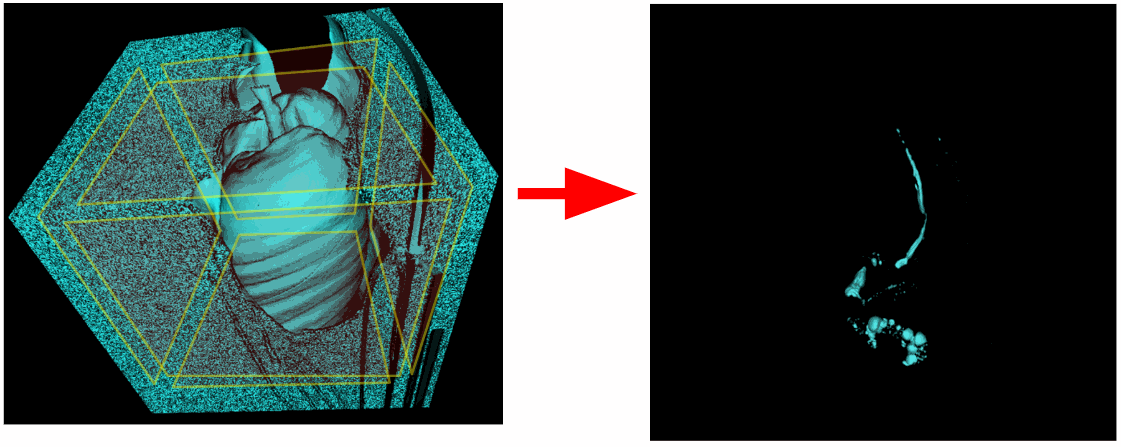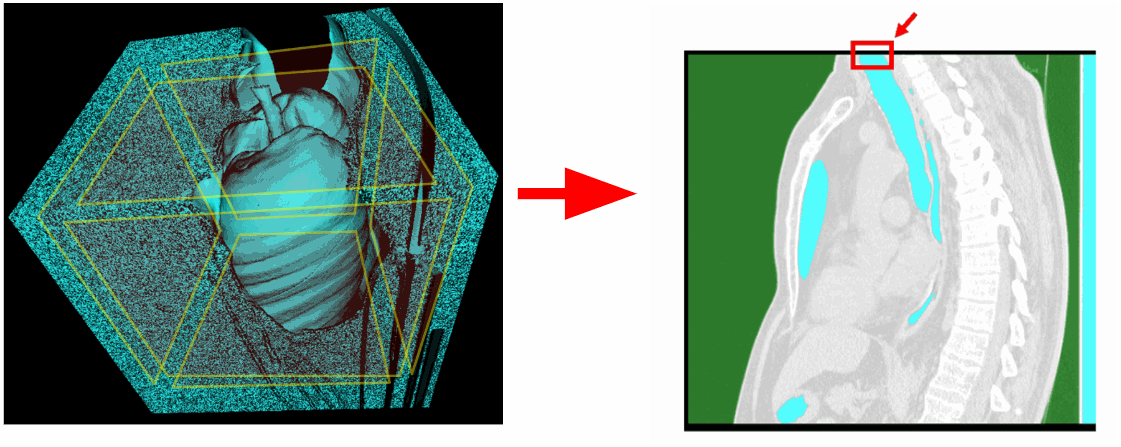
We'll have to exclude the top plane from the scan area. There are also studies in which the lungs were not fully captured and the lower plane is connected to the lungs. So if you wish, you can exclude the lower plane.

But this method works only on chest studies. In the case of the capture of the full volume of the body in the picture will appear the connection of internal and external air through the nasal cavity. Therefore, it is necessary to apply morphological erosion to separate the internal and external air.

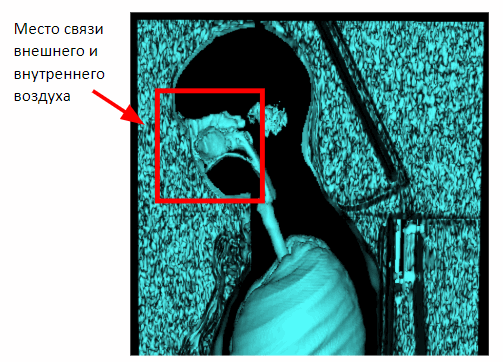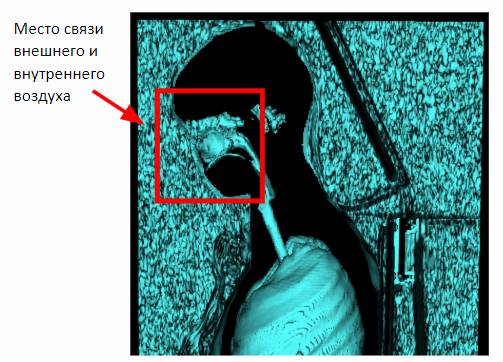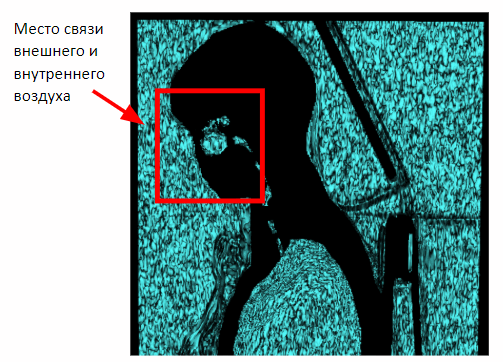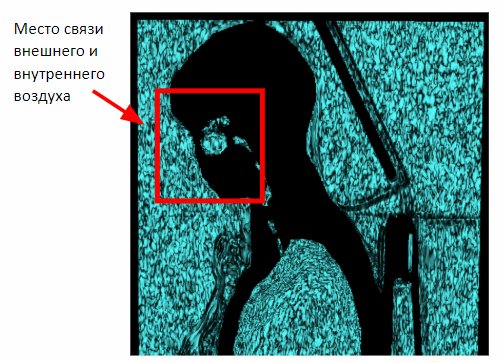
After applying erosion, we can return to the previously obtained method of segmentation of external air on the basis of proximity to the lateral planes of the scene.

Having isolated the outside air, one could immediately take it out of the total volume of air and lungs and get the internal air of the body and lungs. But there is one problem. After erosion, some of the information about the outside air was lost. To restore it, apply dilatation of external air.

Next, subtract the external air from the entire air and respiratory organs and get the internal air and respiratory organs.

The allocation of the maximum volume of the object

Next, select the respiratory organs as the maximum object in volume. The respiratory organs are a separate object. There is no connection between the lungs and the air inside the gastrointestinal tract.

It is worth noting that the correct choice of the X-ray density threshold at the initial step of the threshold conversion is important. Otherwise, in some cases, there may be no connection between the two lungs as a result of low resolution. For example, if we assume that voxels of the respiratory organs have X-ray density of -500 HU or less, then in the case below, the excretion of the respiratory organs as the largest object in volume will lead to an error, since there is no connection between the two lungs. Therefore, the threshold should be increased to -300 HU.

Closing the vessels inside the lungs

A morphological closure, that is, dilatation followed by erosion with the same radius, is applicable to the capture of vessels inside the lungs. X-ray vascular density is about -100..100 HU.

Large blood paths are not closed. But this is not necessary. The purpose of this operation was to destroy the many small holes inside the lungs to simplify further segmentation of the lungs.

Algorithm segmentation of the respiratory organs

As a result, we obtain the following algorithm for segmentation of the respiratory organs:

1. Threshold conversion base volume threshold <-300 HU.
2. Morphological erosion with a radius of 3 mm for the separation of external and internal air.
3. The selection of external air on the basis of proximity to the boundary side planes of the voxel scene.
4. Morphological dilatation of external air to restore information lost due to erosion.
5. Subtract external air from the total air and respiratory organs to obtain internal air and respiratory organs.
6. The selection of the maximum volume of the object.
7. Morphological closure of the vessels inside the lungs.

The implementation of the algorithm in the MATLAB environment

GetRespiratoryOrgans method

function RO = getRespiratoryOrgans(V,cr,ci) %    3D    %  . matFilePath=pwd+"/test_volumes/volume.mat"; load(matFilePath,'V'); %     %   < -300 HU. AL=~imbinarize(V,-300); %    3   %     . SE=strel('sphere',3); EAL=imerode(AL,SE); %       %      . EA=getExternalAir(EAL); %      %      . DEA=EA; for i=1:4 DEA=imdilate(DEA,SE); DEA=DEA&AL; end %         %        . IAL=AL-DEA; %     . RO=getMaxObject(IAL); %     . RO=closeVoxelVolume(RO,3,2); 

GetExternalAir method

 function EA = getExternalAir(EAL) %  bwlabeln  :   %    ,  –    .. V=bwlabeln(EAL); %    ,    %     . R=regionprops3(V,'BoundingBox','VoxelList'); n=height(R); %  3-D      . s=size(EAL); EA=zeros(s,'logical'); %        %    ,   . for i=1:n %   x  y,    %  . x0=R(i,1).BoundingBox(1); y0=R(i,1).BoundingBox(2); x1=x0+R(i,1).BoundingBox(4); y1=y0+R(i,1).BoundingBox(5); %        %  ,       %   EA. if (x0 < 1 || x1 > s(1)-1 || y0 < 1 || y1 > s(2)-1) %        %  : [[x1 y1 z1][x2 y2 z3] … [xn yn zn]]. mat=cell2mat(R(i,2).VoxelList); ms=size(mat); %  ,    . for j=1:ms(1) x=mat(j,2); y=mat(j,1); z=mat(j,3); EA(x,y,z)=1; end end end 

GetMaxObject method

 ###  getMaxObject function [O,m] = getMaxObject(V) %  . V=bwlabeln(V); %        %  . R=regionprops3(V,'Volume','VoxelList'); %      . v=R(:,1).Volume; [m,i]=max(v); %  3-D      % . s=size(V); O=zeros(s,'logical'); %       . mat=cell2mat(R(i,2).VoxelList); ms=size(mat); for j=1:ms(1) x=mat(j,2); y=mat(j,1); z=mat(j,3); O(x,y,z)=1; end 

The source code can be downloaded by reference .

Conclusion

The following articles are planned:

1. segmentation of the trachea and bronchi;
2. lung segmentation;
3. lung lobe segmentation.

The following algorithms will be considered:

1. distance transform;
2. nearest neighbor transform, also known as feature transform;
3. calculation of the eigenvalues ​​of the Hessian matrix for segmentation of flat 3D objects;
4. Watershed segmentation (watershed segmentation).