Dynamic programming in the real world: cutting seams
Dynamic programming has a reputation for a method that you study at a university, and then you only remember it at interviews. But in fact, the method is applicable in many situations. In fact, this is a technique for efficiently solving problems that can be broken down into many strongly repetitive subtasks .
In the article I will show an interesting real-world application of dynamic programming — the task of cutting seams (seam carving). The task and methodology are described in detail in the work of Avidan and Shamir “Cutting out the seams for resizing images with regard to content” (the article is freely available).
This is one of a series of articles on dynamic programming. If you want to brush up on methods, see the illustrated introduction to dynamic programming .
To solve a real problem with dynamic programming, you need to formulate it correctly. This section describes the necessary presets for the selected task.
')
The authors of the original article describe the content-oriented resizing of the image, that is, changing the width or height of the image, taking into account the content. See the original work for details, and I offer a quick overview. Suppose you want to resize a surfer photo:

Top view of the surfer in the middle of a calm ocean, with turbulent waves on the right. Photo: Kiril Dobrev on Pixabay
As described in detail in the article, there are several ways to reduce the width of the image: these are standard cropping and scaling, with their inherent flaws, as well as removing columns of pixels from the middle. As you can imagine, this leaves a visible seam in the photo, where the image on the left and right does not match. And in this way you can remove only a limited amount of image.

Attempting to reduce the width by trimming the left side and cutting the block from the middle. Last leaves visible seam
Avidan and Shamir in the article describe a new technique of "cutting seams" (seam carving). It first determines the less important "low-energy" areas, and then calculates the low-energy "seams" that pass through the picture. In the case of reducing the width of the image is determined by the vertical seam from the top of the image to the bottom, which on each line is shifted to the left or right by no more than one pixel.
In the photo of the surfer, the lowest-energy seam passes through the middle of the image, where the water is the calmest. This corresponds to our intuition.

The lowest-energy seam found on the surfer's image is shown by a red line five pixels wide for visibility, although in fact the seam is only one pixel wide
Having determined the seam with the lowest energy, and then removing it, we reduce the width of the image by one pixel. Repeating this process again and again allows you to significantly reduce the width of the entire photo.

Image of the surfer after reducing the width by 1024 pixels
Again, the algorithm quite logically removed the still water in the middle, as well as on the left side of the photo. But unlike framing, the texture of the water on the left is preserved and there are no sharp transitions. True, you can find some imperfect transitions in the center, but basically the result looks natural.
The magic is to find the lowest energy seam. To do this, we first assign energy to each pixel of the image. Then we use dynamic programming to find the path through the images with the least energy - this algorithm will be discussed in detail in the next section. First, consider how to assign energy values to pixels.
The scientific article discusses several energy functions and their differences. We will not complicate and take a function that simply captures the amount of color change around each pixel. For the sake of completeness, I will describe the energy function in a little more detail in case you want to implement it yourself, but this is just a pre-installation for subsequent calculations of dynamic programming.

Left three pixels from dark to bright. The difference between the first and the last is great. On the right are three dark pixels with a slight difference in color intensity.
To calculate the energy of a particular pixel, we look at the pixels to the left and right of it. Component by component, we calculate the square of the distance between them, that is, the square of the difference between the red, green, and blue components, and then we add them. Do the same for the pixels above and below the center. Finally, we fold the horizontal and vertical distances.
The only caveat is, say, if a pixel is on the left edge, then there is no neighbor on the left. In this case, we make a comparison only with the right pixel. Similar checks are made for pixels on the top, right and bottom edges.
The energy function is great if the neighboring pixels are very different in color, and small if they are similar.
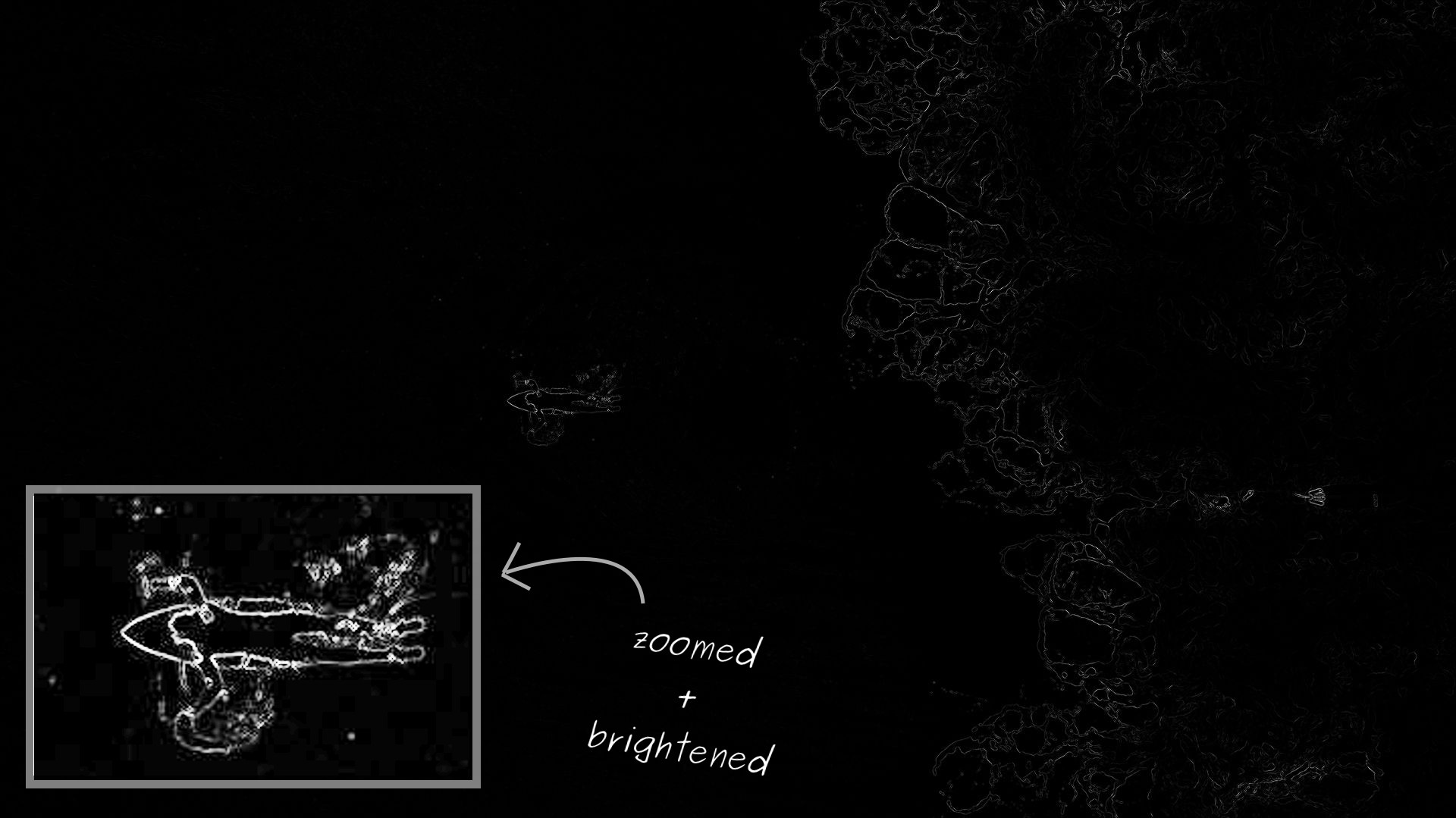
The energy of each pixel in a surfer photo: the lighter - the higher it is. As expected, the surfer has the highest energy in the middle and the turbulent waves on the right.
The energy function works well on a surfer photo. However, it takes a very large range of values. Therefore, when visualizing, it appears that in most of the photos the pixels have zero energy. In fact, there are just very low values compared to the regions with the highest energy. To simplify the visualization, I zoomed in the surfer and covered this area.
By calculating the energy of each pixel, we can find the seam with the lowest energy from the top of the image to the bottom. The same analysis is applicable for horizontal joints to reduce the height of the original image. However, we will focus on vertical.
Let's start with the definition:
It is important to note that the seam with the lowest energy does not necessarily pass through all the pixels with the lowest energy. It takes into account the total energy of all, rather than individual pixels.

Greedy approach does not work. Choosing a low-energy pixel at an early stage, we get stuck in the high-energy region of the image (red path to the right)
As you can see, you can not just choose the pixel with the lowest energy in the next line.
The problem with the greedy approach is that when deciding on the next step, we do not take into account the rest of the seam ahead. We cannot look into the future, but we are able to take into account everything that we already know by now.
Let's turn the task upside down. Instead of choosing between several pixels to continue one seam, we will choose between several seams to go to one pixel . What we need to do is take each pixel and choose between the pixels in the line above, from which the seam can emanate. If each of the pixels in the line above encodes the path traversed to this point, then we are essentially looking at the full story to this point.

For each pixel we study three pixels in the line above. The fundamental choice is which of the seams to continue?
This implies a subtask for each pixel in the image. The subtask should find the best path to a particular pixel, so a good idea would be to associate with each pixel the energy of the lowest-energy seam that ends at that pixel .
Unlike the greedy approach, the above approach essentially tries all possible paths through the image. Just when checking all possible paths, the same subtasks are solved again and again, which makes this approach an ideal option for dynamic programming.
As usual, now we need to formalize the idea into a recurrent relation. There is a subtask corresponding to each pixel in the original image, so the inputs to our recurrence relation may simply be coordinates and this pixel. This provides integer inputs, making it easy to organize subtasks, as well as the ability to store previously calculated values in a two-dimensional array.
Define the function which represents the energy of a vertical seam with the lowest energy. It starts at the top of the image and ends at the pixel. . Title selected as in the original scientific article.
First, you need a base case. All seams, which are completed in the top row, have only one pixel length. Thus, the seam with the minimum energy is just a pixel with the minimum energy:
For the pixels in the remaining rows, we look at the pixels above. Since the seam must be continuous, we consider only three pixels located on the upper left, on the top, and on the upper right. From them, select the seam with the lowest energy, which ends in one of these pixels, and add the energy of the current pixel:
As a border situation, consider the case where the current pixel is located at the left or right edge of the image. In these cases we omit for pixels on the left edge or on the right edge.
Finally, you need to extract the energy of the lowest-energy weld, which covers the entire height of the image. This means that we are looking at the bottom line of the image and choosing the lowest-energy seam that ends at one of these pixels. For photo wide and tall pixels:
So, we got a recurrent relation with all the necessary properties:
Because each subtask corresponds to one pixel of the original image, the dependency graph is very easy to visualize. Simply place them on a two-dimensional grid, as on the original image!
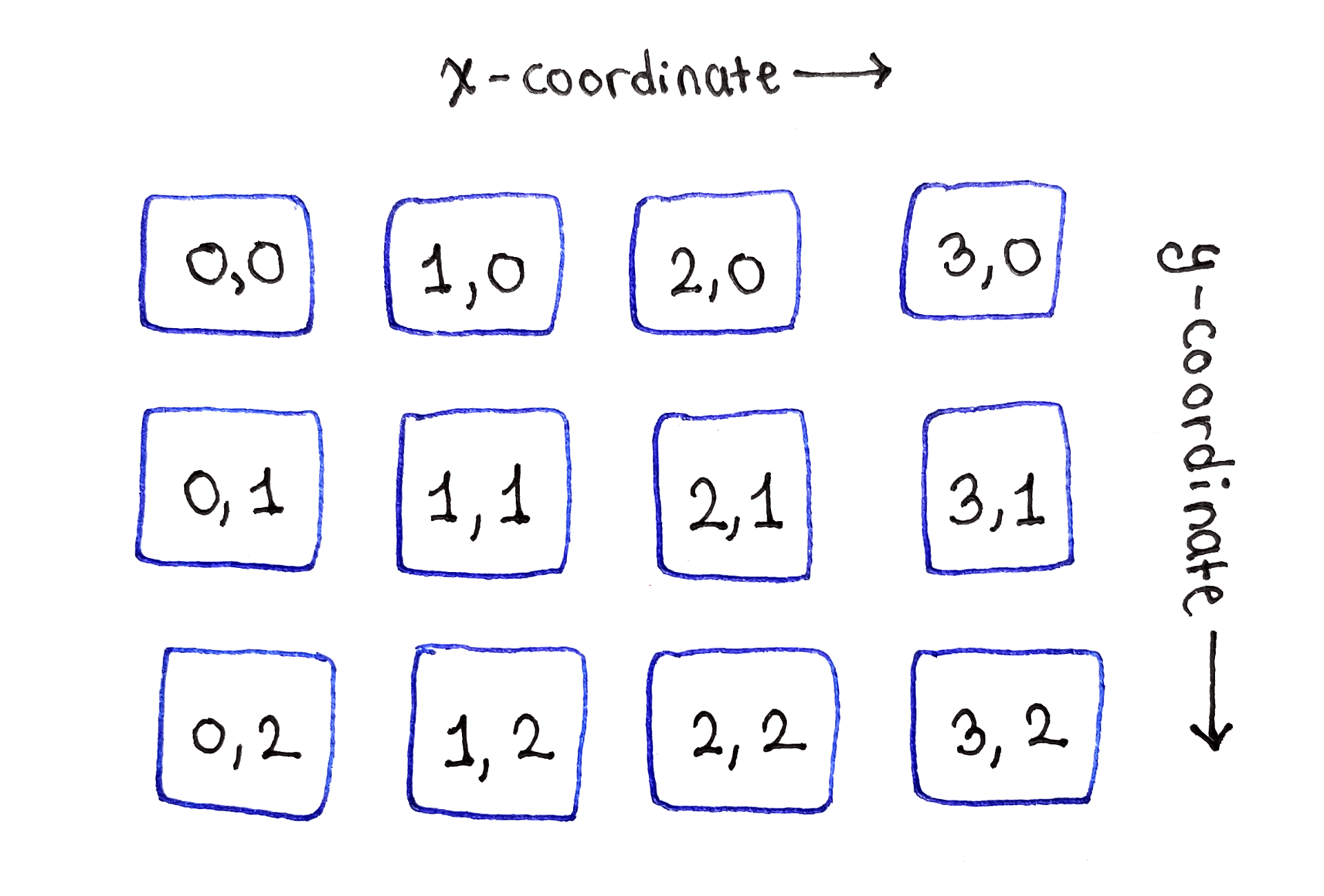
The subtasks are located in a two-dimensional grid, as are the pixels in the original image
As follows from the basic scenario of the recurrence relation, the top line of subtasks can be initialized with the energy values of individual pixels.

The top row does not depend on other subtasks. Note the lack of arrows from the top row of cells.
Dependencies begin to appear in the second line. First, in the leftmost cell in the second line, we are confronted with a borderline situation. Since there are no cells on the left, the cell depends only on the cells located directly above it and on the top right. The same thing will happen later with the leftmost cell in the third row.

Subtasks on the left edge depend only on two subtasks above them.
In the second cell of the second row (1,1), we see the most typical manifestation of the recurrence relation. This cell depends on three cells: top left, right above it and top right. This dependency structure is applied to all “middle” cells in the second and subsequent lines.

The subtasks between the left and right edges depend on the three subtasks above
Finally, the cell from the right edge represents the second borderline situation. Since there are no more cells to the right, it depends only on the cells directly above and above to the left.
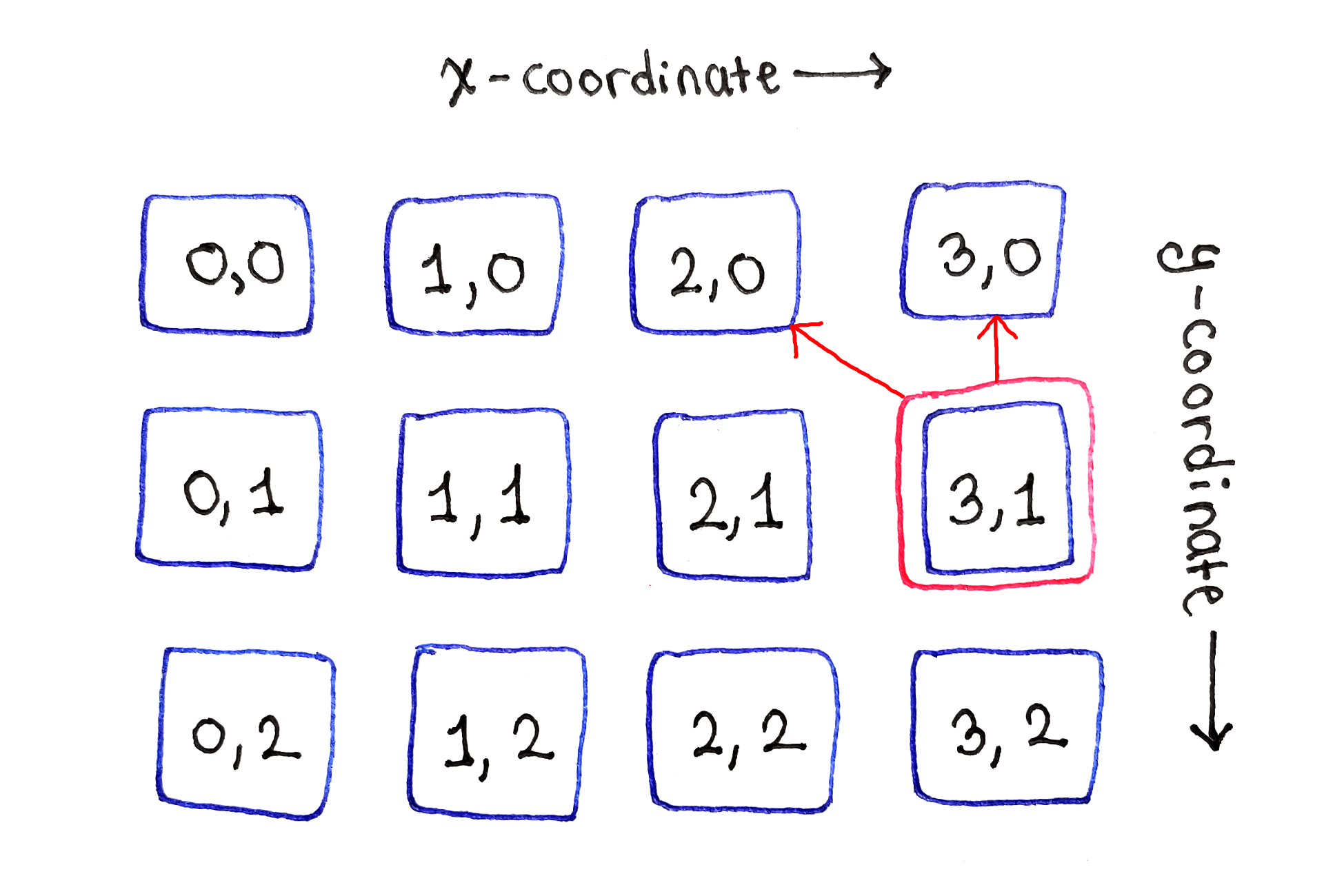
Subtasks on the right edge only depend on two cells above
The process is repeated for all subsequent lines.

Since there are many arrows in the dependency graph, this animation shows dependencies for each subtask in turn.
The full dependency graph scares a lot of arrows, but viewing them one by one helps to set up explicit templates.
After conducting this analysis, we obtained the processing order:
Since each row depends only on the previous one, you need to save only two rows of data: one for the previous row and one for the current row. Moving from left to right, we can even throw away individual elements from the previous line as they are used. However, this complicates the algorithm, since it is necessary to find out which parts of the previous line can be discarded.
In the following Python code, the input is a list of lines, where each line contains a list of numbers representing the individual pixel energies in this line. The input is
Let's start by calculating the energy of the seams of the upper row, simply by copying the individual energies of the pixels in the upper row:
Then we cycle the remaining input lines, calculating the seam energies for each line. The most "difficult" part is to determine which elements of the previous line to refer to, since there are no pixels to the left of the left edge or to the right of the right edge.
At each iteration, a new list of seam energies is created for the current line. At the end of the iteration, we replace the data of the previous line with the data of the current line for the next iteration. Here is how we discard the previous line:
In summary,
You can check this implementation by wrapping the above code in a function, and then calling it with a two-dimensional array that you built. The following inputs are chosen so that the greedy approach fails, with the obvious seam with the lowest energy:
Each pixel in the source image corresponds to one subtask. For each of the subtasks there are no more than three dependencies, so the solution to each of them involves a constant amount of work. The last row passes twice. So for the image width and tall pixel time complexity is equal to .
At each moment of time we have two lists: one for the previous line and one for the current one. In the first elements, and the second gradually increases to . Thus, the spatial complexity is that is just .
Note that if we actually discarded the data elements of the previous line, we would reduce the list of elements of the previous line at about the same speed as the list of the current line grows. Thus, the spatial complexity will remain . Although the width may vary, this is usually not so important.
So, we have found the value of the lowest-energy weld, but what to do with this information? After all, in fact, we are concerned not with the value of energy, but with the seam itself! The problem is that from the end pixel there is no way to return to the rest of the seam.
This is what I missed in previous articles, but the same applies to many of the problems of dynamic programming. For example, if you remember the house robber problem , we have found the maximum value for the amount of robbery, but not what specific houses should be robbed to get this amount.
General answer: store back pointers . In the task of cutting seams, we need not only the value of the seam energy at each pixel. You also need to know which of the pixels in the previous line led to this energy. Keeping this information, we can follow the inverse signs up to the top line, getting the coordinates of all the pixels that make up the seam with the least energy.
First, create a class for storing energy and return pointers. Energy will be used to calculate subtasks. Since the backward pointer determines which pixel in the previous line gave the current energy, we can simply represent it as the x coordinate.
The result of the calculation of each subtask is not just a number, but an instance of this class.
At the end you have to go back through the entire height of the image, following the opposite signs, in order to restore the seam with the least energy. Unfortunately, this means that you need to store pointers for all pixels of the image, and not just for the previous line.
To do this, simply save the full result of all subtasks, although technically you can refuse the numerical energies of the seam of the previous lines. The results are stored in a two-dimensional array, which looks the same as the input array.
Let's start with the first line, which contains only individual pixel energies. Since there is no previous line, all the return pointers are missing, but for consistency, we will still keep instances of
The main loop works basically the same as the previous implementation, with the following differences:
Now the entire table of subtasks is full and we can restore the seam with the least energy. We start by searching for the x coordinate in the bottom line, which corresponds to the seam with the lowest energy:
Now go from the bottom of the image to the top, changing from
So the seam is built from the bottom up, the list can then be read in reverse order, if you need the coordinates from top to bottom.
The time complexity is similar to the previous one, because we still need to process each pixel once. After viewing the last line and searching for the seam with the least energy, we then rise to the full height of the image to restore the seam. So for the image time complexity is equal .
As for volume, we still keep a constant amount of data for each subtask, but now we don’t discard any data. So we use volume .
As soon as a vertical seam with the lowest energy is found, we can simply copy the pixels from the original image to the new one. Each line of the new image contains all the pixels from the corresponding line of the original image, with the exception of the pixel from the seam with the lowest energy. Since we remove one pixel in each row, starting with the image then we get the image .
We can repeat this process by recalculating the energy function in the new image and finding the lowest-energy weld on it. It seems tempting to find more than one low-energy weld in the original image, and then remove them all at once. The problem is that the two seams may intersect. When the first is removed, the second will become invalid, because it lacks one or several pixels.
Animation of the seam removal process. It is better to watch in full screen mode for a clearer view of the seams.
Each frame of the video is an image at each iteration with the overlay visualization of the seam with the least energy.
The article had many detailed explanations, so let's end with a series of beautiful photos! The following photo shows a rock formation in Arches National Park:

Rock formation with a hole in Arches National Park. Photo: Mike Goad on Flickr
The energy function for this image is:

The energy of each pixel in the photo: the lighter - the higher it is. Note the high energy around the edge of the hole.
As a result of the calculation, such a seam is obtained with the lowest energy. Note that it passes through the rock on the right, entering directly into the rock formation where the lighted part at the top of the rock coincides with the color of the sky. Perhaps you should choose a better energy function!

The lowest-energy seam found in the image is shown with a red line five pixels wide for visibility, although in fact the seam is only one pixel wide
Finally, the image of the arch after resizing:

Arch after compression at 1024 pixels
The result is definitely not perfect: many of the edges of the mountain from the original image are distorted. One improvement could be the implementation of one of the other energy functions listed in a scientific article.
Although dynamic programming is usually discussed in theory, it is a useful practical method for solving complex problems. In this article, we looked at one of the applications of dynamic programming: resizing an image based on content by cutting out seams.
We applied the same principles of splitting the task into smaller subtasks, analyzing the dependencies between these subtasks, and then solving the subtasks in a manner that minimizes the spatial and temporal complexity of the algorithm. In addition, we studied the use of backward pointers to not only find the energy value for the optimal seam, but also to determine the coordinates of each pixel that made up this value. Then they applied these parts to the real problem, which requires some pre- and post-processing for truly effective use of the dynamic programming algorithm.
In the article I will show an interesting real-world application of dynamic programming — the task of cutting seams (seam carving). The task and methodology are described in detail in the work of Avidan and Shamir “Cutting out the seams for resizing images with regard to content” (the article is freely available).
This is one of a series of articles on dynamic programming. If you want to brush up on methods, see the illustrated introduction to dynamic programming .
Resizing images with content
To solve a real problem with dynamic programming, you need to formulate it correctly. This section describes the necessary presets for the selected task.
')
The authors of the original article describe the content-oriented resizing of the image, that is, changing the width or height of the image, taking into account the content. See the original work for details, and I offer a quick overview. Suppose you want to resize a surfer photo:

Top view of the surfer in the middle of a calm ocean, with turbulent waves on the right. Photo: Kiril Dobrev on Pixabay
As described in detail in the article, there are several ways to reduce the width of the image: these are standard cropping and scaling, with their inherent flaws, as well as removing columns of pixels from the middle. As you can imagine, this leaves a visible seam in the photo, where the image on the left and right does not match. And in this way you can remove only a limited amount of image.

Attempting to reduce the width by trimming the left side and cutting the block from the middle. Last leaves visible seam
Avidan and Shamir in the article describe a new technique of "cutting seams" (seam carving). It first determines the less important "low-energy" areas, and then calculates the low-energy "seams" that pass through the picture. In the case of reducing the width of the image is determined by the vertical seam from the top of the image to the bottom, which on each line is shifted to the left or right by no more than one pixel.
In the photo of the surfer, the lowest-energy seam passes through the middle of the image, where the water is the calmest. This corresponds to our intuition.

The lowest-energy seam found on the surfer's image is shown by a red line five pixels wide for visibility, although in fact the seam is only one pixel wide
Having determined the seam with the lowest energy, and then removing it, we reduce the width of the image by one pixel. Repeating this process again and again allows you to significantly reduce the width of the entire photo.

Image of the surfer after reducing the width by 1024 pixels
Again, the algorithm quite logically removed the still water in the middle, as well as on the left side of the photo. But unlike framing, the texture of the water on the left is preserved and there are no sharp transitions. True, you can find some imperfect transitions in the center, but basically the result looks natural.
Image Energy Definition
The magic is to find the lowest energy seam. To do this, we first assign energy to each pixel of the image. Then we use dynamic programming to find the path through the images with the least energy - this algorithm will be discussed in detail in the next section. First, consider how to assign energy values to pixels.
The scientific article discusses several energy functions and their differences. We will not complicate and take a function that simply captures the amount of color change around each pixel. For the sake of completeness, I will describe the energy function in a little more detail in case you want to implement it yourself, but this is just a pre-installation for subsequent calculations of dynamic programming.

Left three pixels from dark to bright. The difference between the first and the last is great. On the right are three dark pixels with a slight difference in color intensity.
To calculate the energy of a particular pixel, we look at the pixels to the left and right of it. Component by component, we calculate the square of the distance between them, that is, the square of the difference between the red, green, and blue components, and then we add them. Do the same for the pixels above and below the center. Finally, we fold the horizontal and vertical distances.
The only caveat is, say, if a pixel is on the left edge, then there is no neighbor on the left. In this case, we make a comparison only with the right pixel. Similar checks are made for pixels on the top, right and bottom edges.
The energy function is great if the neighboring pixels are very different in color, and small if they are similar.

The energy of each pixel in a surfer photo: the lighter - the higher it is. As expected, the surfer has the highest energy in the middle and the turbulent waves on the right.
The energy function works well on a surfer photo. However, it takes a very large range of values. Therefore, when visualizing, it appears that in most of the photos the pixels have zero energy. In fact, there are just very low values compared to the regions with the highest energy. To simplify the visualization, I zoomed in the surfer and covered this area.
Find low-energy welds with dynamic programming
By calculating the energy of each pixel, we can find the seam with the lowest energy from the top of the image to the bottom. The same analysis is applicable for horizontal joints to reduce the height of the original image. However, we will focus on vertical.
Let's start with the definition:
- A seam is a sequence of pixels, one pixel per line. The requirement is that between two consecutive lines the coordinate varies by no more than one pixel. This saves the seam sequence.
- The seam with the lowest energy is the one whose total energy over all the pixels in the seam is minimized.
It is important to note that the seam with the lowest energy does not necessarily pass through all the pixels with the lowest energy. It takes into account the total energy of all, rather than individual pixels.

Greedy approach does not work. Choosing a low-energy pixel at an early stage, we get stuck in the high-energy region of the image (red path to the right)
As you can see, you can not just choose the pixel with the lowest energy in the next line.
We break a problem into subtasks
The problem with the greedy approach is that when deciding on the next step, we do not take into account the rest of the seam ahead. We cannot look into the future, but we are able to take into account everything that we already know by now.
Let's turn the task upside down. Instead of choosing between several pixels to continue one seam, we will choose between several seams to go to one pixel . What we need to do is take each pixel and choose between the pixels in the line above, from which the seam can emanate. If each of the pixels in the line above encodes the path traversed to this point, then we are essentially looking at the full story to this point.

For each pixel we study three pixels in the line above. The fundamental choice is which of the seams to continue?
This implies a subtask for each pixel in the image. The subtask should find the best path to a particular pixel, so a good idea would be to associate with each pixel the energy of the lowest-energy seam that ends at that pixel .
Unlike the greedy approach, the above approach essentially tries all possible paths through the image. Just when checking all possible paths, the same subtasks are solved again and again, which makes this approach an ideal option for dynamic programming.
Determination of the recurrence ratio
As usual, now we need to formalize the idea into a recurrent relation. There is a subtask corresponding to each pixel in the original image, so the inputs to our recurrence relation may simply be coordinates and this pixel. This provides integer inputs, making it easy to organize subtasks, as well as the ability to store previously calculated values in a two-dimensional array.
Define the function which represents the energy of a vertical seam with the lowest energy. It starts at the top of the image and ends at the pixel. . Title selected as in the original scientific article.
First, you need a base case. All seams, which are completed in the top row, have only one pixel length. Thus, the seam with the minimum energy is just a pixel with the minimum energy:
For the pixels in the remaining rows, we look at the pixels above. Since the seam must be continuous, we consider only three pixels located on the upper left, on the top, and on the upper right. From them, select the seam with the lowest energy, which ends in one of these pixels, and add the energy of the current pixel:
As a border situation, consider the case where the current pixel is located at the left or right edge of the image. In these cases we omit for pixels on the left edge or on the right edge.
Finally, you need to extract the energy of the lowest-energy weld, which covers the entire height of the image. This means that we are looking at the bottom line of the image and choosing the lowest-energy seam that ends at one of these pixels. For photo wide and tall pixels:
So, we got a recurrent relation with all the necessary properties:
- The recurrence relation has integer inputs.
- From the ratio is easy to extract the final answer.
- The ratio depends on oneself.
DAG subtask check (oriented acyclic graph)
Because each subtask corresponds to one pixel of the original image, the dependency graph is very easy to visualize. Simply place them on a two-dimensional grid, as on the original image!

The subtasks are located in a two-dimensional grid, as are the pixels in the original image
As follows from the basic scenario of the recurrence relation, the top line of subtasks can be initialized with the energy values of individual pixels.

The top row does not depend on other subtasks. Note the lack of arrows from the top row of cells.
Dependencies begin to appear in the second line. First, in the leftmost cell in the second line, we are confronted with a borderline situation. Since there are no cells on the left, the cell depends only on the cells located directly above it and on the top right. The same thing will happen later with the leftmost cell in the third row.

Subtasks on the left edge depend only on two subtasks above them.
In the second cell of the second row (1,1), we see the most typical manifestation of the recurrence relation. This cell depends on three cells: top left, right above it and top right. This dependency structure is applied to all “middle” cells in the second and subsequent lines.

The subtasks between the left and right edges depend on the three subtasks above
Finally, the cell from the right edge represents the second borderline situation. Since there are no more cells to the right, it depends only on the cells directly above and above to the left.

Subtasks on the right edge only depend on two cells above
The process is repeated for all subsequent lines.

Since there are many arrows in the dependency graph, this animation shows dependencies for each subtask in turn.
The full dependency graph scares a lot of arrows, but viewing them one by one helps to set up explicit templates.
Implementation from the bottom up
After conducting this analysis, we obtained the processing order:
- Go from the top of the image to the bottom.
- Each line can act in any order. The natural choice is to go from left to right.
Since each row depends only on the previous one, you need to save only two rows of data: one for the previous row and one for the current row. Moving from left to right, we can even throw away individual elements from the previous line as they are used. However, this complicates the algorithm, since it is necessary to find out which parts of the previous line can be discarded.
In the following Python code, the input is a list of lines, where each line contains a list of numbers representing the individual pixel energies in this line. The input is
pixel_energies , and pixel_energies[y][x] represents the pixel energy in coordinates .Let's start by calculating the energy of the seams of the upper row, simply by copying the individual energies of the pixels in the upper row:
previous_seam_energies_row = list(pixel_energies[0]) Then we cycle the remaining input lines, calculating the seam energies for each line. The most "difficult" part is to determine which elements of the previous line to refer to, since there are no pixels to the left of the left edge or to the right of the right edge.
At each iteration, a new list of seam energies is created for the current line. At the end of the iteration, we replace the data of the previous line with the data of the current line for the next iteration. Here is how we discard the previous line:
# Skip the first row in the following loop. for y in range(1, len(pixel_energies)): pixel_energies_row = pixel_energies[y] seam_energies_row = [] for x, pixel_energy in enumerate(pixel_energies_row): # Determine the range of x values to iterate over in the previous # row. The range depends on if the current pixel is in the middle of # the image, or on one of the edges. x_left = max(x - 1, 0) x_right = min(x + 1, len(pixel_energies_row) - 1) x_range = range(x_left, x_right + 1) min_seam_energy = pixel_energy + \ min(previous_seam_energies_row[x_i] for x_i in x_range) seam_energies_row.append(min_seam_energy) previous_seam_energies_row = seam_energies_row In summary,
previous_seam_energies_row contains the seam energies for the bottom line. We find the minimum value in this list - and this is the answer! min(seam_energy for seam_energy in previous_seam_energies_row) You can check this implementation by wrapping the above code in a function, and then calling it with a two-dimensional array that you built. The following inputs are chosen so that the greedy approach fails, with the obvious seam with the lowest energy:
ENERGIES = [ [9, 9, 0, 9, 9], [9, 1, 9, 8, 9], [9, 9, 9, 9, 0], [9, 9, 9, 0, 9], ] print(min_seam_energy(ENERGIES)) Spatial and temporal complexity
Each pixel in the source image corresponds to one subtask. For each of the subtasks there are no more than three dependencies, so the solution to each of them involves a constant amount of work. The last row passes twice. So for the image width and tall pixel time complexity is equal to .
At each moment of time we have two lists: one for the previous line and one for the current one. In the first elements, and the second gradually increases to . Thus, the spatial complexity is that is just .
Note that if we actually discarded the data elements of the previous line, we would reduce the list of elements of the previous line at about the same speed as the list of the current line grows. Thus, the spatial complexity will remain . Although the width may vary, this is usually not so important.
Reverse pointers for finding the seam with the lowest energy
So, we have found the value of the lowest-energy weld, but what to do with this information? After all, in fact, we are concerned not with the value of energy, but with the seam itself! The problem is that from the end pixel there is no way to return to the rest of the seam.
This is what I missed in previous articles, but the same applies to many of the problems of dynamic programming. For example, if you remember the house robber problem , we have found the maximum value for the amount of robbery, but not what specific houses should be robbed to get this amount.
Return Pointer Representation
General answer: store back pointers . In the task of cutting seams, we need not only the value of the seam energy at each pixel. You also need to know which of the pixels in the previous line led to this energy. Keeping this information, we can follow the inverse signs up to the top line, getting the coordinates of all the pixels that make up the seam with the least energy.
First, create a class for storing energy and return pointers. Energy will be used to calculate subtasks. Since the backward pointer determines which pixel in the previous line gave the current energy, we can simply represent it as the x coordinate.
class SeamEnergyWithBackPointer(): def __init__(self, energy, x_coordinate_in_previous_row=None): self.energy = energy self.x_coordinate_in_previous_row = x_coordinate_in_previous_row The result of the calculation of each subtask is not just a number, but an instance of this class.
Reverse Pointer Storage
At the end you have to go back through the entire height of the image, following the opposite signs, in order to restore the seam with the least energy. Unfortunately, this means that you need to store pointers for all pixels of the image, and not just for the previous line.
To do this, simply save the full result of all subtasks, although technically you can refuse the numerical energies of the seam of the previous lines. The results are stored in a two-dimensional array, which looks the same as the input array.
Let's start with the first line, which contains only individual pixel energies. Since there is no previous line, all the return pointers are missing, but for consistency, we will still keep instances of
SeamEnergyWithBackPointers : seam_energies = [] # Initialize the top row of seam energies by copying over the top row of # the pixel energies. There are no back pointers in the top row. seam_energies.append([ SeamEnergyWithBackPointer(pixel_energy) for pixel_energy in pixel_energies[0] ]) The main loop works basically the same as the previous implementation, with the following differences:
- The data for the previous line contains instances of
SeamEnergyWithBackPointer, so when calculating the value of the recurrence relation, you should look for the seam energy inside these objects. - To save the data for the current pixel, you need to build a new instance of
SeamEnergyWithBackPointer. Here we will store the seam energy for the current pixel, as well as the x coordinate from the previous line, used to calculate the current seam energy. - At the end of each line, instead of discarding the data of the previous line, we simply add the data of the current line to
seam_energies.
# Skip the first row in the following loop. for y in range(1, len(pixel_energies)): pixel_energies_row = pixel_energies[y] seam_energies_row = [] for x, pixel_energy in enumerate(pixel_energies_row): # Determine the range of x values to iterate over in the previous # row. The range depends on if the current pixel is in the middle of # the image, or on one of the edges. x_left = max(x - 1, 0) x_right = min(x + 1, len(pixel_energies_row) - 1) x_range = range(x_left, x_right + 1) min_parent_x = min( x_range, key=lambda x_i: seam_energies[y - 1][x_i].energy ) min_seam_energy = SeamEnergyWithBackPointer( pixel_energy + seam_energies[y - 1][min_parent_x].energy, min_parent_x ) seam_energies_row.append(min_seam_energy) seam_energies.append(seam_energies_row) We go on the opposite signs
Now the entire table of subtasks is full and we can restore the seam with the least energy. We start by searching for the x coordinate in the bottom line, which corresponds to the seam with the lowest energy:
# Find the x coordinate with minimal seam energy in the bottom row. min_seam_end_x = min( range(len(seam_energies[-1])), key=lambda x: seam_energies[-1][x].energy ) Now go from the bottom of the image to the top, changing from
len(seam_energies) - 1 to zero. At each iteration we add the current pair. to the list representing our seam and then set the value for the object pointed to by SeamEnergyWithBackPointer in the current line. # Follow the back pointers to form a list of coordinates that form the # lowest-energy seam. seam = [] seam_point_x = min_seam_end_x for y in range(len(seam_energies) - 1, -1, -1): seam.append((seam_point_x, y)) seam_point_x = \ seam_energies[y][seam_point_x].x_coordinate_in_previous_row seam.reverse() So the seam is built from the bottom up, the list can then be read in reverse order, if you need the coordinates from top to bottom.
Spatial and temporal complexity
The time complexity is similar to the previous one, because we still need to process each pixel once. After viewing the last line and searching for the seam with the least energy, we then rise to the full height of the image to restore the seam. So for the image time complexity is equal .
As for volume, we still keep a constant amount of data for each subtask, but now we don’t discard any data. So we use volume .
Removing low-energy joints
As soon as a vertical seam with the lowest energy is found, we can simply copy the pixels from the original image to the new one. Each line of the new image contains all the pixels from the corresponding line of the original image, with the exception of the pixel from the seam with the lowest energy. Since we remove one pixel in each row, starting with the image then we get the image .
We can repeat this process by recalculating the energy function in the new image and finding the lowest-energy weld on it. It seems tempting to find more than one low-energy weld in the original image, and then remove them all at once. The problem is that the two seams may intersect. When the first is removed, the second will become invalid, because it lacks one or several pixels.
Animation of the seam removal process. It is better to watch in full screen mode for a clearer view of the seams.
Each frame of the video is an image at each iteration with the overlay visualization of the seam with the least energy.
Another example
The article had many detailed explanations, so let's end with a series of beautiful photos! The following photo shows a rock formation in Arches National Park:

Rock formation with a hole in Arches National Park. Photo: Mike Goad on Flickr
The energy function for this image is:

The energy of each pixel in the photo: the lighter - the higher it is. Note the high energy around the edge of the hole.
As a result of the calculation, such a seam is obtained with the lowest energy. Note that it passes through the rock on the right, entering directly into the rock formation where the lighted part at the top of the rock coincides with the color of the sky. Perhaps you should choose a better energy function!

The lowest-energy seam found in the image is shown with a red line five pixels wide for visibility, although in fact the seam is only one pixel wide
Finally, the image of the arch after resizing:

Arch after compression at 1024 pixels
The result is definitely not perfect: many of the edges of the mountain from the original image are distorted. One improvement could be the implementation of one of the other energy functions listed in a scientific article.
Although dynamic programming is usually discussed in theory, it is a useful practical method for solving complex problems. In this article, we looked at one of the applications of dynamic programming: resizing an image based on content by cutting out seams.
We applied the same principles of splitting the task into smaller subtasks, analyzing the dependencies between these subtasks, and then solving the subtasks in a manner that minimizes the spatial and temporal complexity of the algorithm. In addition, we studied the use of backward pointers to not only find the energy value for the optimal seam, but also to determine the coordinates of each pixel that made up this value. Then they applied these parts to the real problem, which requires some pre- and post-processing for truly effective use of the dynamic programming algorithm.
Source: https://habr.com/ru/post/458110/
All Articles