The symmetry property of the cointegration relation
If we study cointegration purely theoretically, it is easy to prove that if a series A cointegrated with B then a series B cointegrated with A . However, if we start to investigate co-integration empirically, it turns out that the theoretical calculations are not always confirmed. Why it happens?
Symmetry
Attitude A called symmetric if A s u b s e t e q A - 1 where A - 1 - inverse relationship determined by the condition: x A - 1 y tantamount to y A x . In other words, if the relation is satisfied x A y then the relation y A x .
Consider two I ( 1 ) row x t and y t , t = 0 , d o t s , T . Cointegration is symmetric if y t = b e t a 1 x t + v a r e p s i l o o n 1 t attracts xt= beta2yt+ varepsilon2t , that is, if the presence of a direct regression leads to the presence of a reverse.
')
Consider the equation yt= beta1xt+ varepsilon1t , beta1 neq0 . Change the left and right sides of the places and subtract varepsilon1t from both parts: beta1xt=yt− varepsilon1t . Because beta1 neq0 by definition, we divide both parts into beta1 :
xt= frac1 beta1yt− frac varepsilon1t beta1.
Replace 1/ beta1 on beta2 , but − varepsilon1t/ beta1 on varepsilon2t get xt= beta2yt+ varepsilon2t . Therefore, the cointegration ratio is symmetric.
It follows that if a variable X cointegrated with variable Y then variable Y must be cointegrated with variable X . However, Angle-Granger test for cointegration does not always confirm this symmetry property, since sometimes the variable Y not cointegrated with variable X according to this test.
I tested the symmetry property on the 2017 data of the Moscow and New York stock exchanges using the Angle-Granger test. There were 7975 cointegrated pairs of shares on the Moscow Stock Exchange. For 7731 (97%) cointegrated pairs, the symmetry property was confirmed, for 244 (3%) cointegrated couples, the symmetry property was not confirmed.
There were 140903 cointegrated pairs of shares on the New York Stock Exchange. For 136586 (97%) cointegrated pairs, the symmetry property was confirmed, for 4317 (3%) cointegrated couples, the symmetry property was not confirmed.
Interpretation
This result can be interpreted by the low power and high probability of an error of the second kind of Dickie-Fuller test, on which Angle-Granger test is based. The probability of an error of the second kind can be denoted by beta=P(H0|H1) then the value 1− beta called the power of the test. Unfortunately, the Dickey-Fuller test is not able to distinguish between non-stationary and near-non-stationary time series.
What is a near-non-stationary time series? Consider a time series xt= phixt−1+ varepsilont . A stationary time series is a series in which 0< phi<1 . A non-stationary time series is a series in which phi=1 . Near-non-stationary time series is called such a series in which the value phi close to one.
In the case of near-nonstationary time series, we are often unable to reject the null hypothesis of nonstationarity. This means that the Dicky-Fuller test has a high risk of an error of the second kind, that is, the probability of not rejecting the false null hypothesis.
KPSS test
A possible answer to the weakness of the Dickie-Fuller test is the KPSS test, which is named after the initials of the scientists Kwiatkowski, Phillips, Schmidt and Shin. Although the methodical approach of this test is completely different from the Dickey-Fuller approach, the main difference should be understood in the permutation of the null and alternative hypotheses.
In the KPSS test, the null hypothesis states that the time series is stationary, versus the alternative about the presence of non-stationarity. Near-non-stationary time series, which were often detected as non-stationary using the Dickey-Fuller test, can be correctly identified as stationary using the KPSS test.
However, we must be aware that any results of statistical testing are only probabilistic, and should not be confused with some true judgment. There is always a non-zero probability that we are mistaken. For this reason, the combination of Dickie-Fuller and KPSS test results is proposed as an ideal test for non-stationarity.
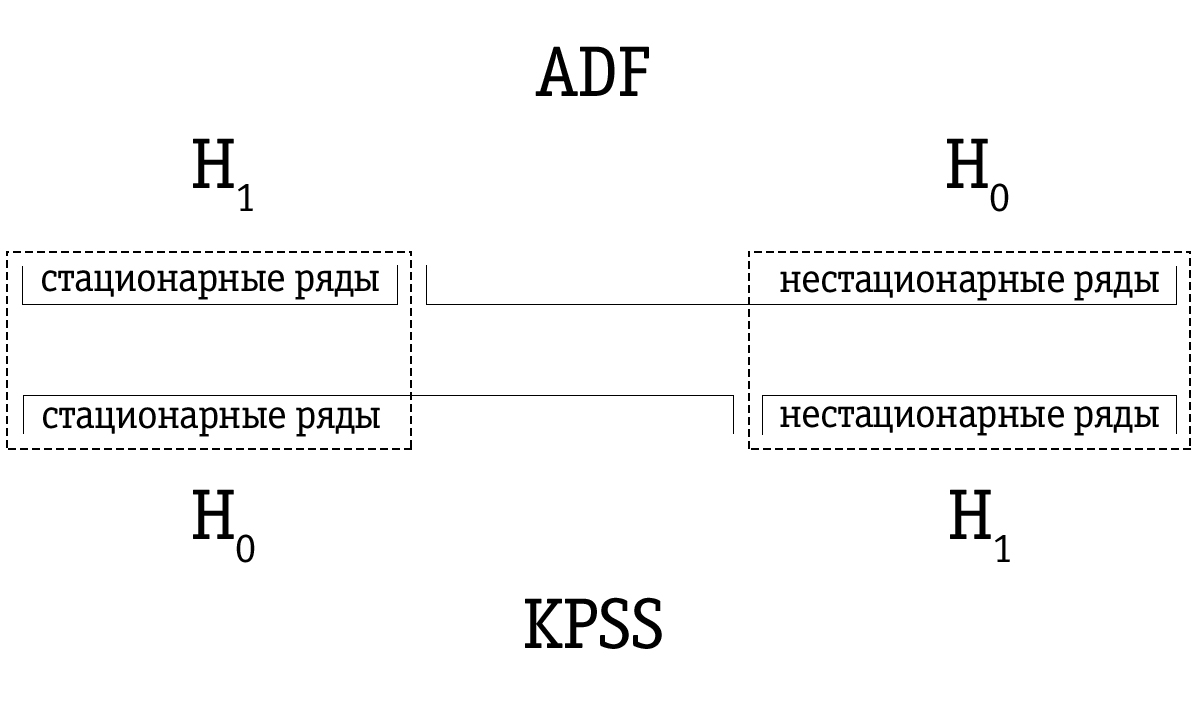
Due to the low power, the Dickey-Fuller test often mistakenly identifies the series as non-stationary, therefore the resultant set of time series identified by the Dickie-Fuller test as non-stationary turns out to be larger compared to the set of time series identified by the KPSS test. Therefore, the order of testing is important.
If the time series is identified as stationary using the Dickey-Fuller test, then it will most likely also be identified as stationary using the KPSS test; in this case, we can assume that the series is indeed stationary.
If the time series was identified as non-stationary using the KPSS test, then it will most likely also be detected as non-stationary using the Dickey-Fuller test; in this case, we can assume that the series is indeed non-stationary.
However, it often happens that a time series that was identified as non-stationary using the Dickey-Fuller test will be marked as stationary using the KPSS test. In that case, we must be very careful with our final conclusion. We can check how strong the base is for stationarity in the case of the KPSS test and for non-stationarity in the case of the Dickey-Fuller test and make the appropriate decision. Of course, we can also leave the question of the stationarity of such a time series unresolved.
The KPSS test approach assumes that the time series yt tested for stationarity relative to the trend, can be decomposed into the sum of the deterministic trend betat random walk rt and stationary errors varepsilont :
yt= betat+rt+ varepsilont,rt=rt−1+ut,
Where ut - normal iid process with zero mean and variance sigma2 ( ut simN(0, sigma2) ). Initial value r0 treated as fixed and plays the role of a free member. Stationary error varepsilont It can be generated by any common ARMA process, that is, it can have strong autocorrelation.
Similar to the Dickie-Fuller test, the ability to take into account an arbitrary autocorrelation structure varepsilont very important, because most economic time series strongly depend on time and, therefore, have strong autocorrelation. If we want to test stationarity about the horizontal axis, then the member betat simply excluded from the equation above.
From the equation above it follows that the null hypothesis H0 about stationarity yt equivalent to hypothesis sigma2=0 from which it follows that rt=r0 for all t ( r0 - constant). Similarly, the alternative hypothesis H1 about nonstationarity is equivalent to a hypothesis sigma2 neq0 .
To test the hypothesis H0 : sigma2=0 (stationary time series) versus alternative H1 : sigma2 neq0 (non-stationary time series) the authors of the KPSS test receive one-sided statistics of the Lagrange multipliers test. They also calculate its asymptotic distribution and model asymptotic critical values. We do not consider theoretical details here, but only briefly describe the test execution algorithm.
When performing a KPSS test for a time series yt , t=1, dots,T the least squares method (least squares) is used to evaluate one of the following equations:
yt=a0+ varepsilont,yt=a0+ betat+ varepsilont.
If we want to test stationarity with respect to the horizontal axis, we estimate the first equation. If we plan to test stationarity with respect to the trend, we choose the second equation.
Leftovers et from the estimated equation are used to calculate the statistics of the Lagrange multipliers test. The Lagrange multipliers test is based on the idea that when the null hypothesis is fulfilled, all Lagrange multipliers should be zero.
Lagrange multipliers test
The Lagrange multiplier test is associated with a more general approach to estimating parameters using the maximum likelihood method (ML). According to this approach, data are considered as evidence relating to distribution parameters. The evidence is expressed as a function of unknown parameters - the likelihood function:
L(X1,X2,X3, dots,Xn; Phi1, Phi2, dots, Phik),
Where Xi - observed values, and Phii - parameters that we want to evaluate.
Maximum likelihood function is the combined probability of sampling observations
L(X1,X2,X3, dots,Xn; Phi1, Phi2, dots, Phik)=P(X1 landX2 landX3 dotsXn).
The goal of the maximum likelihood method is to maximize the likelihood function. This is achieved by differentiating the maximum probability function for each of the estimated parameters and equating the partial derivatives to zero. The values of the parameters at which the value of the function is maximal is the desired estimate.
Usually, to simplify the subsequent work, the logarithm of the likelihood function is first taken.
Consider a generalized linear model. Y= betaX+ varepsilon where it is assumed that varepsilon normally distributed N(0, sigma2) , i.e Y− betaX simN(0, sigma2) .
We want to test the hypothesis that the system is executed q ( q<k a) independent linear constraints R beta=r . Here R - known q timesk rank matrix q , but r - famous q times1 vector.
For each pair of observed values X and Y will exist under the condition of normality probability density function of the following form:
f(Xi,Yi)= frac1 sqrt2 pi sigma2e− frac12 left( fracYi− betaXi sigma right)2.
Provided n joint observations X and Y The total probability of observing all values in a sample is equal to the product of the individual values of the probability density function. Thus, the likelihood function is defined as follows:
L( beta)= prod limitsni=1 frac1 sqrt2 pi sigma2e− frac12 left( fracYi− betaXi sigma right)2.
Since it is easier to differentiate the sum than the product, it usually takes the logarithm of the likelihood function, thus:
lnL( beta)= sum limitsni=1 left( ln frac1 sqrt2 pi sigma2− frac12 sigma2(Yi− betaXi)2 right).
This useful conversion does not affect the final result, because lnL Is an increasing function L . So, that value beta which maximizes lnL will also maximize L .
ML-score for beta in regression with constraint ( R beta=r ) obtained by maximizing the function lnL( beta) provided R beta=r . To find this estimate, we write the Lagrange function:
psi( beta)= lnL( beta)−g′(R beta−r),
where through g= left(g1, dots,gq right)′ marked vector q Lagrange multipliers.
Statistics test Lagrange multipliers, denoted by eta mu in the case of stationarity about the horizontal axis and through eta tau in the case of stationarity relative to the trend, is determined by the expression
eta mu/ tau=T2 frac1s2(l) sum limitsTt=1S2t,
Where
St= sum limitsti=1ei
and
s2(l)=T−1 sum limitsTt=1e2t+2T−1 sum limitsl1w(s,l) sum limitsTt=s+1etets,
Where
w(s,l)=1− fracsl+1.
In the above equations St - process of partial amount of balances et from the estimated equation; s2(l) - assessment of long-term residual dispersion et ; but w(s,l) - the so-called spectral window of Bartlett, where l - the lag truncation parameter.
In this application, the spectral window is used to estimate the spectral error density for a certain interval (window) that moves throughout the range of the series. Data outside the interval is ignored, since the window function is a function that is zero outside a certain selected interval (window).
Dispersion score s2(l) depends on parameter l as well as l increases and more than 0, the score s2(l) begins to take into account possible autocorrelation in residuals et .
Finally, Lagrange multipliers test statistics eta mu or eta tau compared with critical values. If the statistics of the Lagrange multipliers test exceeds the corresponding critical value, then the null hypothesis H0 (stationary time series) deviates in favor of an alternative hypothesis H1 (non-stationary time series). Otherwise, we cannot reject the null hypothesis. H0 about stationarity of the time series.
Critical values are asymptotic and, therefore, most suitable for large sample sizes. However, in practice they are also used for a small sample. Moreover, the critical values are independent of the parameter. l . However, the statistics of the Lagrange multipliers test will depend on the parameter l . The authors of the KPSS test do not offer any general algorithm for selecting the appropriate parameter. l . Usually the test is performed for l ranging from 0 to 8.
By increasing l we are less likely to reject the null hypothesis H0 about stationarity, which partly leads to a decrease in the power of the test and can give mixed results. However, in general, it can be said that if the null hypothesis H0 about stationarity of the time series is not rejected even at small values l (0, 1 or 2), we conclude that the time series tested are stationary.
Comparison of test results
To assess the probability of symmetry, the following methodology was developed.
- All time series are checked for 1st order integrability using the Dickey-Fuller test at a significance level of 0.05. Below, we consider only integrable series of the 1st order.
- From the integrable series of the first order obtained in Section 1, pairs are made by combining without repetitions.
- Pairs of stocks compiled in paragraph 2 are tested for cointegration using the Angle-Granger test. As a result, cointegrated pairs are identified.
- Regression residues obtained as a result of testing in clause 3 are tested for stationarity using the KPSS test. Thus, the results of the two tests are combined.
- The time series in cointegrated pairs from Section 2 are interchanged and again checked for cointegration using the Angle-Granger test, that is, we investigate whether the relationship between the time series is symmetric.
- The time series in cointegrated pairs from p. 4 are interchanged and the regression residuals are again checked for stationarity using the KPSS test, that is, we examine whether the relationship between the time series is symmetrical.
All calculations are performed using the MATLAB package. The results are presented in the table below. For each test, we have a number of relationships that are symmetrical in the test results (marked S ); we have a number of relationships that are not symmetrical on the test results (marked ¬S ); and we have an empirical probability that the ratio is symmetric on the test results ( P(S)= fracSS+¬S ).
On the Moscow Stock Exchange:
| Test | ADF | ADF + KPSS |
|---|---|---|
| S | 7731 | sixteen |
| ¬S | 244 | one |
| P(s) | 97% | 94% |
On the New York Stock Exchange:
| Test | ADF | ADF + KPSS |
|---|---|---|
| S | 136586 | 182 |
| ¬S | 4317 | 7 |
| P(s) | 97% | 96% |
Backtest results comparison
Let's compare the results of a trading strategy based on historical data for cointegrated pairs selected using the Angle Granger test, and for cointegrated pairs selected using the KPSS test.
| Criteria | ADF | ADF + KPSS |
|---|---|---|
| The number of symmetrical pairs | 6417 | 205 |
| Maximum profit | 340.31% | 287.35% |
| Maximum loss | -53.28% | -46.35% |
| Steam traded in plus | 2904 | 113 |
| Steam traded to zero | 293 | 3 |
| Steam traded in minus | 3220 | 89 |
| Average annual yield | 13.51% | 22.72% |
As can be seen from the table, thanks to a more accurate identification of cointegrated pairs of shares, it was possible to increase the average annual yield when trading as a separate cointegrated pair by 9.21%. Thus, the proposed methodology can increase the profitability of algorithmic trading when using market neutral strategies.
Alternative interpretation
As we saw above, the Angle-Granger test results are a lottery. My thoughts will seem to someone too categorical, but I think that it makes a lot of sense not to take for granted the null hypothesis, confirmed by statistical analysis.
The conservatism of the scientific hypothesis testing method is that when analyzing data, we can draw only one valid conclusion: the null hypothesis deviates at a chosen level of significance. This does not mean that the alternative is correct. H1 - we just received indirect evidence of its likelihood on the basis of the typical “evidence from the opposite”. When true H0 The researcher is also instructed to make only a cautious conclusion: based on the data obtained in the experimental conditions, it was not possible to find enough evidence to reject the null hypothesis.
In unison with my thoughts in September 2018, an article was written written by influential people and urging to abandon the concept of “statistical significance” and the testing paradigm of the null hypothesis.
Most importantly: “Such proposals as changing the level of the threshold p -the default values, the use of confidence intervals with an emphasis on whether they contain zero or not, or the use of the Bayes coefficient along with universally accepted classifications to assess the strength of evidence that comes from all the same or similar problems as the current use p -values with a level of 0.05 ... are a form of statistical alchemy that makes a false promise to transform randomness into authenticity, the so-called “laundering of uncertainty” (Gelman, 2016), which begins with data and ends with dichotomous conclusions about truth or falsity - binary statements that "there is an effect" or "no effect" is based on the achievement of some p -values or other threshold values.
Accepting uncertainty and variability of effects (Carlin, 2016; Gelman, 2016), recognizing that we can learn more (much more) about the world, rejecting the false promise of certainty offered by such a dichotomization will be a critical step forward. ”
findings
We saw that although the symmetry property of the cointegration relation should theoretically be satisfied, the experimental data disagree with the theoretical calculations. One of the interpretations of this paradox is the low power of the Dicky-Fuller test.
As a new methodology for identifying cointegrated asset pairs, it was proposed to test regression residues obtained using the Angle-Granger test for stationarity using the KPSS test and combine the results of these tests; and combine the Angle-Granger test and the KPSS test for both direct and reverse regression.
Backtests were conducted on the data of the Moscow Exchange for 2017. According to the results of backtests, the average annual yield using the above methodology for identifying cointegrated pairs of shares was 22.72%. Thus, compared to identifying cointegrated pairs of shares using the Angle-Granger test, we managed to increase the average annual yield by 9.21%.
An alternative version of the interpretation of the paradox - do not take for granted the null hypothesis, confirmed by statistical analysis. The testing paradigm of the null hypothesis and the dichotomy offered by such a paradigm give us a false sense of market knowledge.
When I first began my research, it seemed to me that it was possible to take the market, stick it into the “meat grinder” of statistical tests, and get filtered tasty rows at the exit. Unfortunately, now I see that this concept of statistical brute force will not work.
Whether there is a cointegration in the market or not - for me this question remains open. I still have big questions for the pioneers of this theory. Previously, I had some kind of trepidation by the West and those scientists who developed financial mathematics at a time when in the Soviet Union econometrics was considered the selling maid of the bourgeoisie. It seemed to me that we were very far behind, and somewhere there in Europe and America there are gods of finance who have learned the holy grail of truth.
Now I understand that European and American scientists are not much different from ours, the only difference is in the scale of quackery. Our scientists sit in an ivory castle, write some kind of nonsense and get grants of 500 thousand rubles for this. In the West, about the same scientists are sitting in about the same ivory castle, they write about the same nonsense and receive for this “nobel prizes” and grants of 500 thousand dollars in size. That's the whole difference.
At the moment I do not have an unequivocal view on the subject of my research. Appealing to the fact that “all hedge funds use trading in pairs” I think is wrong, because most hedge funds just as well go bankrupt.
, , .
Source: https://habr.com/ru/post/457794/
All Articles