Javascript programming for lathe

This article should be called “generating combinations of guitar gears from a Chinese lathe for selecting a feed pitch using a JavaScript script,” but this doesn’t sound so intriguing.


The cheapest Lathe with Aliexpress MX-180V has been surprisingly amusing me since its appearance in my home workshop for more than half a year. Despite the fact that the Chinese have forgotten to fasten it to the box, as a result of which the front panel was rumpled.


Despite the inability of this device to cut the left-hand thread, contrary to the oaths of the seller that it can. In spite of the fact that the screwdriver included in the package, was scattered after the first touch to it.
')


Despite, finally, the poor quality of the device, I use it, I make the parts I need and, in general, I accumulate a skill. For me, the beauty of home machines is that you don’t have to rummage through trash, looking for something similar to something necessary, but just do it yourself. This is the most direct way from idea to realization.
So, gradually, it came to the cutting threads. I decided to train on a nail with a diameter of 6 mm, which means that in order not to grind anything, this will be a bolt diameter with a pitch of 1 mm for which I had a nut. According to the table, which is located on the machine body, I found the necessary gear combination for the selected step.


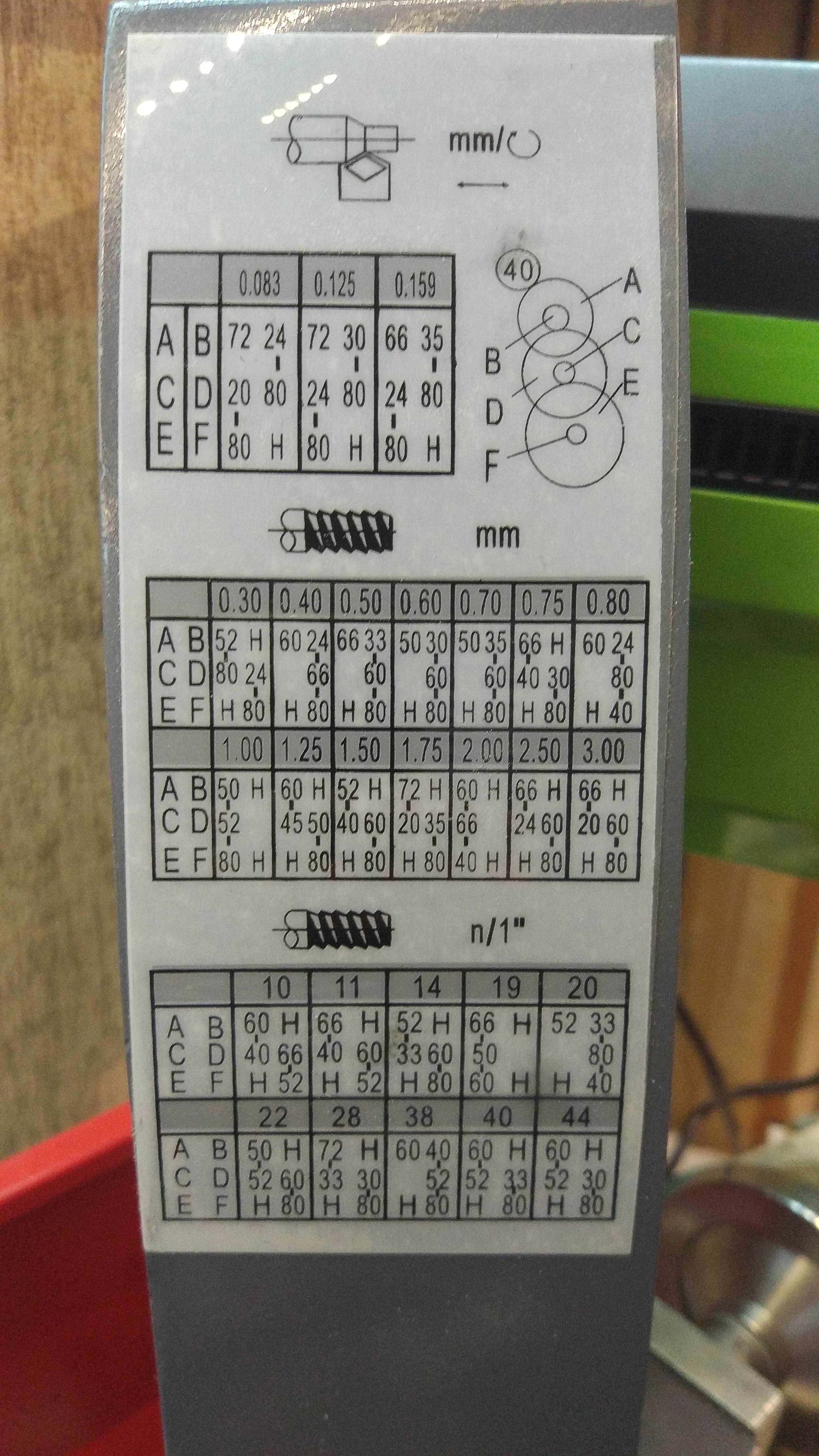
There is a gear with 80 teeth on the shaft, then 52, and between this gear and the spindle there should be a gear with 50 teeth. But among the 10 gears in my kit with 50 teeth was not.


Then I began to get upset once again, well, how is it, brothers Chinese! Finally I was finished off by the fact that in my set there was also no second gear for 80 teeth and 66, and 33-tooth gears. A little thought, I realized that for feeding in 1 mm per revolution, it is important only the ratio of teeth on the spindle and on the shaft, and the intermediate gears can be any, the main thing is that they fit there. As a result, the first thread in its life M6x1 using a cutter, not a die, I cut!


One thing only darkened the joy of this event, the discrepancy between the table and the available gears. This meant that now I could not just take it, look at the table and cut the necessary thread when necessary. We have to think every time how to put the gears, every time re-count. In general, the table is much more convenient. So fate made me delve into the details of the construction of the guitar and the subtleties of calculating the gear ratios of the gearboxes.

The gearbox device is not difficult and schematically four ways of installing gears (regardless of their diameters) can be represented as follows:


For definiteness, we call them chaining schemes. It was necessary for me to find out which combinations of gears are permissible from the point of view of the possibility of installing them in a guide rail, which can rotate around the shaft axis and on which two axes of intermediate gears are fixed.


The upper axis should not touch the spindle pulley, and therefore the first driven gear should not have less than 52 teeth. In addition, the guide rail should not be turned too close to the spindle shaft, in order to avoid touching the tachometer magnets.


A physical attempt at brute force of this task showed that there are quite a lot of valid combinations. On the piece of paper, there was already not enough space for the yet untested kits, I became confused. There was a great chance to skip the combination, or vice versa, write down the already tested one. The desire to engage in a blind search of options, sitting in an uncomfortable position in front of the machine, evaporated very quickly. How many and what combinations and feeds are possible on this machine? It was necessary to call for help theory, and to work on the enumeration of options to lay on the computer, so that in vain did not stand.


It will be necessary to find or write a generator of placements without repetitions, since each gear I have is only in one instance. There are many ways to choose from 10 variants of 3, 4 and 5 gears, but some of them should obviously be discarded due to geometrical considerations. You will need a filter that only passes appropriate gear sets. After filtering, there will most likely be many combinations that will give the same feed pitch, without differing in the engagement patterns and gear sets, i.e. there will be equivalent permutations. From them, too, should get rid of.

Without hesitation, I decided to program in JS, although I could have done it in C ++, but in my practice I have not yet encountered a task that could not be solved in browser JS, when it does not go to resetting the data to disk. In this way, I am attracted by the minimalism and sufficiency of the infrastructure, notepad and browser, everything else is superfluous. The language gives algorithms, the browser - a graphical interface, an interpreter and a debugger. Any library can either be quickly written by yourself, or found and downloaded. When you are not engaged in industrial or commercial programming, it is enough, simply, a universal calculator.

I found the placement generator and adapted it quickly. Its purpose in the program is to rearrange the indices of the array in which copies of gears will be stored. Here, in the search function, placements are generated, and the passed filters are pushed into the result array by the test function. In addition, the feed rate is calculated in the last function. For definiteness, we denote all gears as in the figure.


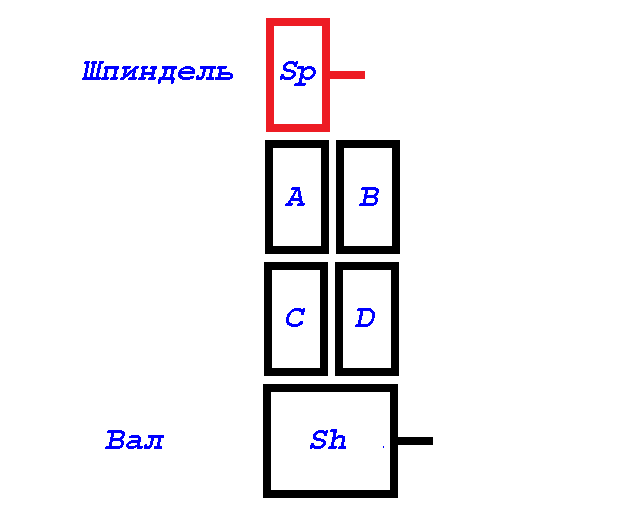
We write out the formulas for calculating the feed, as a function of the pitch of the feed shaft and the number of gear teeth for each of the engagement patterns:


To develop a filter, it is necessary to elaborate on the geometric parameters of the guitar. The axes of the spindle, shaft and upper intermediate gear form a triangle.

The side L of which is measured directly, and the rest is calculated from the radii of the gears. The radius of the gears is less than their outer radius by the amount of overlap when meshing. Since the gears are not perfectly made, the amount of overlap should be established empirically. The overlap must be such that it ensures the engagement, but prevents the gears from seizing. In my case, it turned out to be 1 mm. The following limitation is imposed on the S side, the axis of the upper intermediate gear should not touch the spindle pulley. It is measured directly when the guide with the axis in the upper position is turned as close as possible to the spindle, the axis should almost touch the pulley. The distance V cannot be greater than the distance between the axis of the shaft and the upper intermediate axis pushed all the way up the slot. You should also impose a restriction on the angle between L and V. Turning the rail without gears and axes as close as possible to the spindle, measure or calculate the distance S between the spindle axis and the top point of the guide and calculate the angle using the formula


Here V is the distance from the shaft axis to the top point of the guide, and not to the top point of the groove (this can be an arbitrary rail point, as long as the distances V and S are measured to it). By the same formula, the angle will be calculated during testing, but the distances S and V will depend on the radii of the gears.


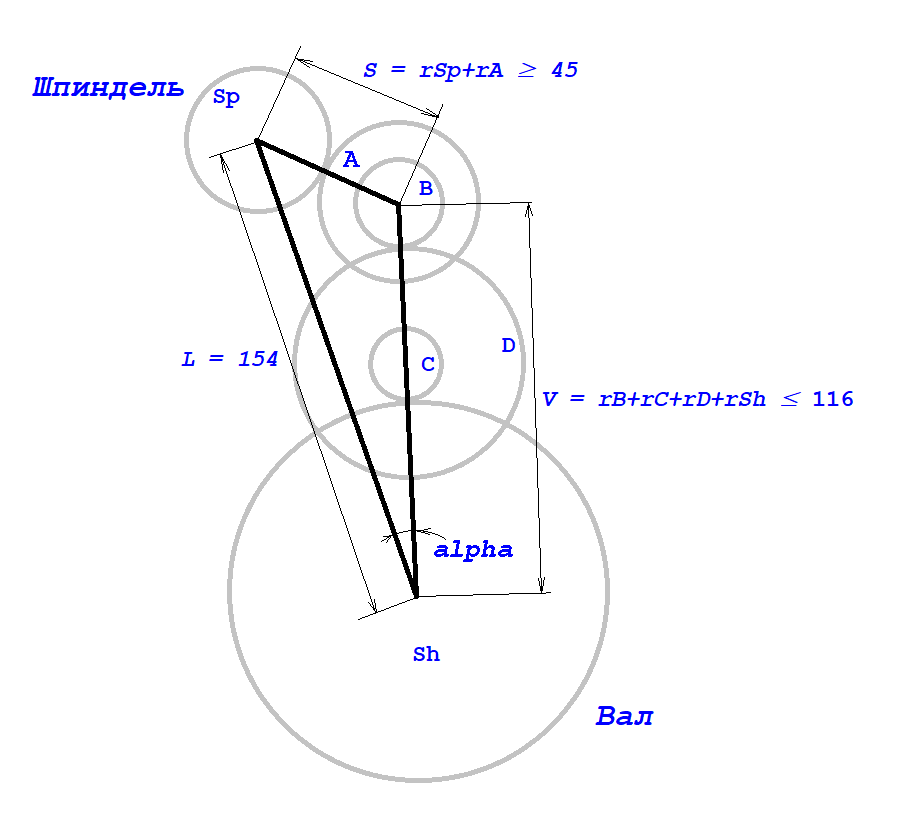
In addition, gear B can not be greater than A, and C can not be greater than D. D should not touch the shaft, and C should not cling to A, when engaged with B and D.

After the list of successful combinations is built, you should save it from redundancy using the eliminate function. This is done by a simple search for solutions that are unique in any respect. You can use the uniqueness of the step, or the uniqueness of a set of gears and the like.

In my case, we get 751 combinations that differ in pitch, number of gears and their set. There are only 222 unique innings. Of course, many of them are not commonly used or not used at all, but inch ones are present.


Working on this text I did not leave the thought that the way to solve this problem is at the level of grade 5, which is even embarrassing to talk about. Just in this case, the result (innings table) is much more important than the way it is received. However, machine tools, guitars, gearboxes, gears can each be different and it would not be bad to have at least one of the approaches to constructing such a table.

In conclusion, I cite the full text of the script, which is supplied with a sufficient number of comments, taking into account the above.