Utreexo: compress UTXO Bitcoin set

Hi, Habr!

On the Bitcoin network, all nodes agree on a lot of UTXOs during consensus: how many coins are available for spending, to whom, and under what conditions. The UTXO set is the minimum data set required for the validator node, without which the node will not be able to verify the validity of incoming transactions and blocks containing them.

In this regard, attempts are being made in every way to reduce the stored representation of this set, compress it without losing security guarantees. The smaller the amount of stored data, the lower the requirements for the disk space of the validator node, which makes starting the validator node cheap, allows you to grow the network and thereby increase the stability of the network.

In this post we’ll write down a Rust-prototype of a recent proposal from the co-author of Lightning Network Paper , Thaddeus Dryja - Utreexo: a dynamic hash-based accumulator for the Bitcoin UTXO set , which reduces the space requirements for validator nodes.

What is the problem?

One of the eternal problems of Bitcoin was its scalability. The idea of ​​“a bank itself” requires network members to keep records of all means available for use. In Bitcoin, the available funds are expressed as a set of unspent outputs - UTXO-set. Although this is not a particularly intuitive view, it is advantageous from the point of view of the performance of the implementation, compared to the view in which each “wallet” has a “balance” in a separate record, and also adds privacy (for example, it provides CoinJoin ).

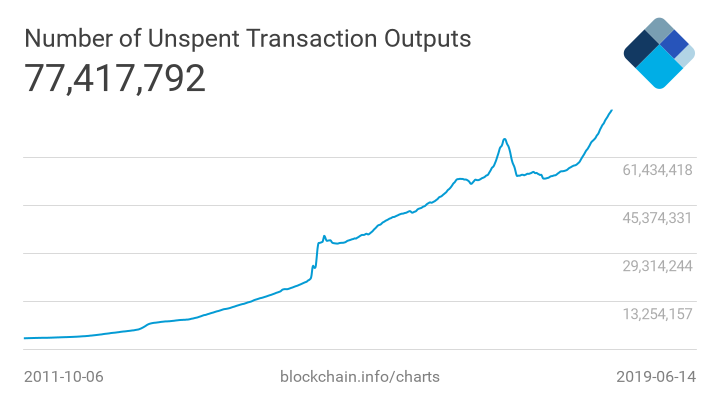
It is important to distinguish between transaction history (what is called a blockchain) and the current state of the system. Bitcoin transaction history currently occupies about 200 GB of disk space, and continues to grow. However, the state of the system is much less, about 4 GB, and takes into account only the fact of ownership of coins by anyone at the present time. The volume of this data also increases over time, but at a much slower rate and sometimes even tends to decrease (see KDPV).

Light clients (SPV) exchange security guarantees for the ability to store no minimum state (UTXO-set), except for private keys.

UTXO and UTXO-set

UTXO (Unspent Transaction Output) - unspent transaction output, the end point of each Satoshi journey transmitted in transactions. Unspent exits become inputs of new transactions and at the same time spend (spend) and are deleted from the UTXO-set.

New UTXOs are always created by transactions:

• coinbase transactions without entries: create new UTXOs during the coin issue by miners
• regular transactions: create new UTXOs, while spending a certain set of existing UTXOs

The process of working with UTXO: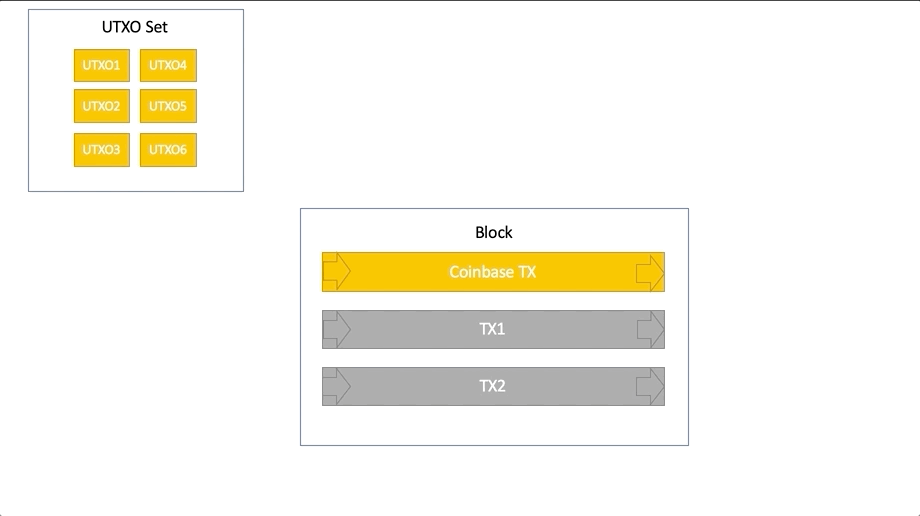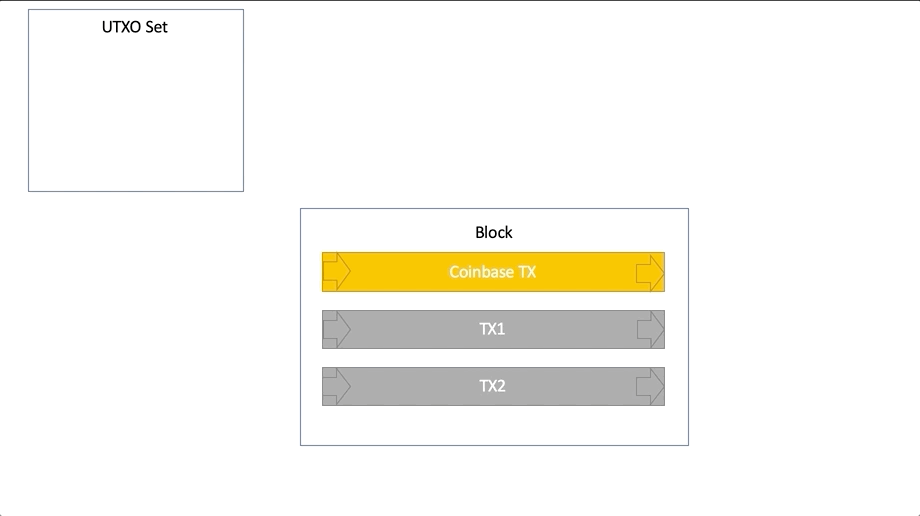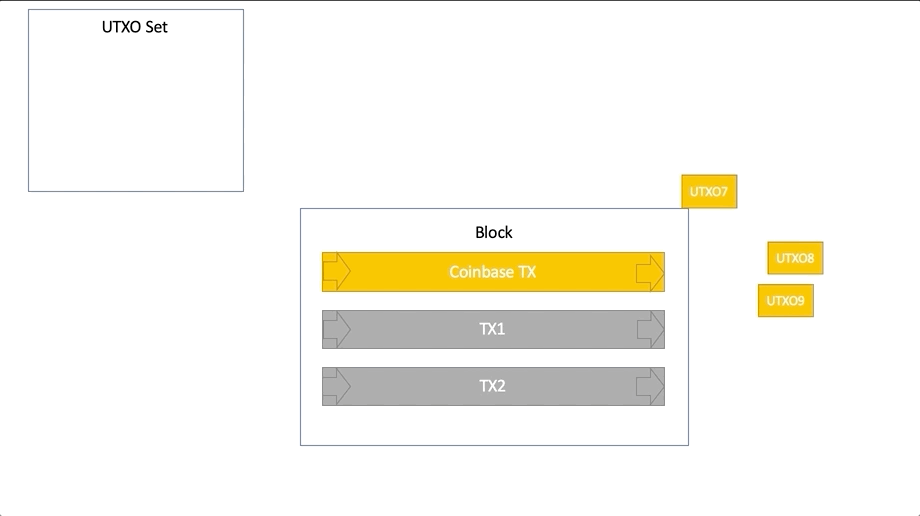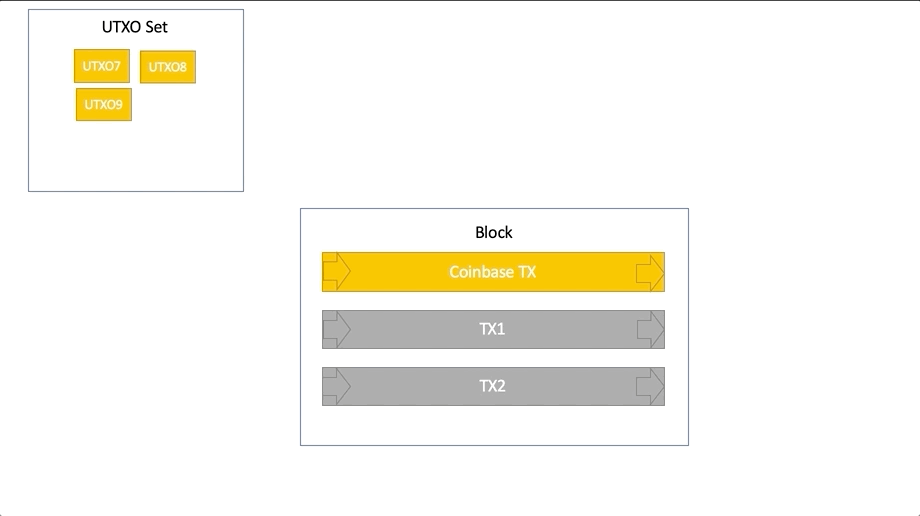

Wallets consider the number of coins available for spending (balance) based on the amount of UTXO available to this wallet for spending.

Each node validator, in order to prevent double spend attempts, must track the collection of all UTXOs when checking each transaction of each block.

The node must have logic:

• UTXO-set Additions
• Deletes from UTXO-set
• Checks for the presence of a single UTXO in the set

There are ways to reduce the requirements for stored information about the set, while retaining the ability to add and delete items, check and prove the existence of an item in a set using cryptographic batteries .

Batteries for UTXO

The idea of ​​using batteries to store a variety of UTXO was discussed earlier .

UTXO-set is built on the fly, during the initial download of a block chain (IBD, initial block download), stored in full and permanently, while its contents change after processing transactions from each new and correct network block. This process requires downloading approximately 200 GB of data blocks and verifying hundreds of millions of digital signatures. After the IBD process is completed, the UTXO-set will occupy about 4 GB in the bottom line.

However, when using batteries, the rules of consensus regarding the means are reduced to checking and generating cryptographic evidence, and the burden of tracking the available funds is shifted onto the shoulders of the owner of these funds, which provides evidence of their presence and ownership.

A battery can be called a compact representation of a set. The size of the stored view, however, must either be constant $$$O (1)$ or increase sublinearly relative to the power of the set and size of the element itself, for example $$$O (log (n))$ where n is the power of the stored set.

In doing so, the battery should allow generation of evidence of the inclusion of the element in the set (inclusion proof) and to be able to effectively verify this evidence.

A battery is called dynamic if it allows you to add elements and remove elements from the set.

An example of such a battery is the RSA battery offered by Boneh, Bunz, Fisch in December 2018 . Such a battery has a constant size of the stored representation, but requires a shared secret (trusted setup). This requirement negates the applicability of such a battery for trustless networks such as Bitcoin, since data leakage when generating a secret could allow attackers to create fake evidence of the existence of UTXO, deceiving nodes from the UTXO-set on the basis of such a battery.

Utreexo

The Utreexo design proposed by Thaddeus Dryja allows you to create a dynamic battery without a trusted-setup.

Utreexo is a forest of perfect binary Merkle Trees and is a development of ideas presented in Efficient asynchronous accumulators for distributed pki , adding the ability to remove elements from the set.

Battery Logical Structure

The elements of the battery are located in the form of a forest of ideal binary trees. The trees are ordered by height. This view is selected as the most visual and allows you to visualize the merging of trees during battery operations.

The author notes that since all the trees of a forest are ideal, their height is expressed by a power of two, as well as any natural number can be represented as a sum of powers of two. Accordingly, any set of sheets can be grouped in the form of binary trees, and in all cases, adding a new element requires knowledge of only the root nodes of the stored trees .

Thus, the Utreexo battery's stored representation is a list of root nodes (Merkle root), and not the entire forest of trees .

Imagine a list of root elements as Vec<Option<Hash>> . The optional Option<Hash> indicates that the root element may be missing, which means that there is no tree in the battery with the appropriate height.

 /// SHA-256  #[derive(Copy, Clone, Hash, Eq, PartialEq)] pub struct Hash(pub [u8; 32]); #[derive(Debug, Clone)] pub struct Utreexo { pub roots: Vec<Option<Hash>>, } impl Utreexo { pub fn new(capacity: usize) -> Self { Utreexo { roots: vec![None; capacity], } } } 

Adding items

To begin with, we describe the parent() function, which recognizes a parent node for two given elements.

 fn hash(bytes: &[u8]) -> Hash { let mut sha = Sha256::new(); sha.input(bytes); let res = sha.result(); let mut res_bytes = [0u8; 32]; res_bytes.copy_from_slice(res.as_slice()); Hash(res_bytes) } fn parent(left: &Hash, right: &Hash) -> Hash { let concat = left .0 .into_iter() .chain(right.0.into_iter()) .map(|b| *b) .collect::<Vec<_>>(); hash(&concat[..]) } 

In the course of adding elements to the battery, you need to keep track of which root elements are changed. By following the path of changing the root elements for each element added, you can later construct a proof of the presence of these elements.

 #[derive(Debug)] pub struct Update<'a> { pub utreexo: &'a mut Utreexo, // ProofStep  ""     pub updated: HashMap<Hash, ProofStep>, } 

To add an element to the battery, you need:

• Create an array of baskets of root elements new_roots and place the existing root elements there, one for each basket:

 let mut new_roots = Vec::new(); for root in self.roots.iter() { let mut vec = Vec::<Hash>::new(); if let Some(hash) = root { vec.push(*hash); } new_roots.push(vec); } 

• Add added items (array of insertions ) to the first basket new_roots[0] :

 new_roots[0].extend_from_slice(insertions); 

• To carry out a "union" (coalescing) of the elements added to the first basket with the rest:
  
  • For all baskets with more than one item:
    
    1. We take two elements from the end of the basket, we calculate their parent, we delete both elements
    2. Add the computed parent to the next bin.

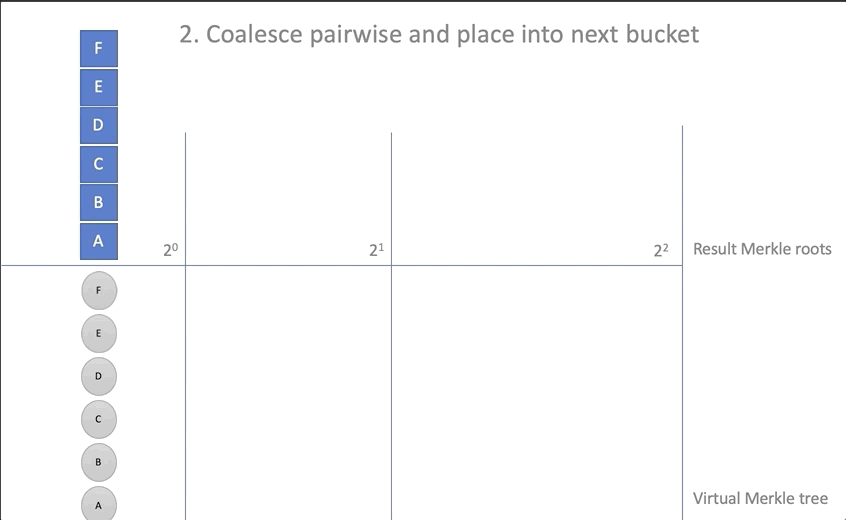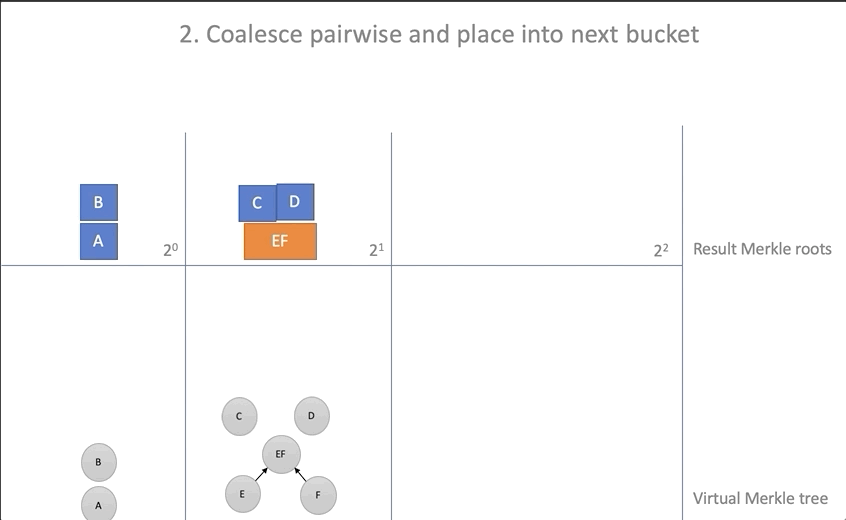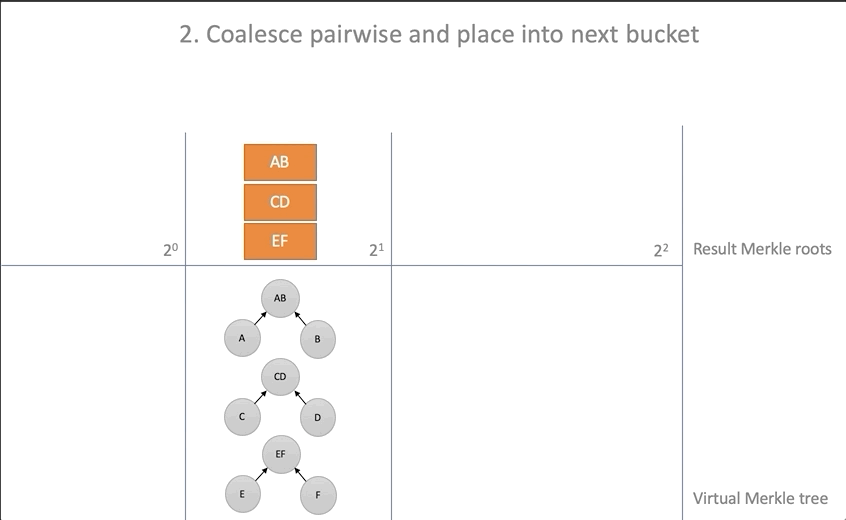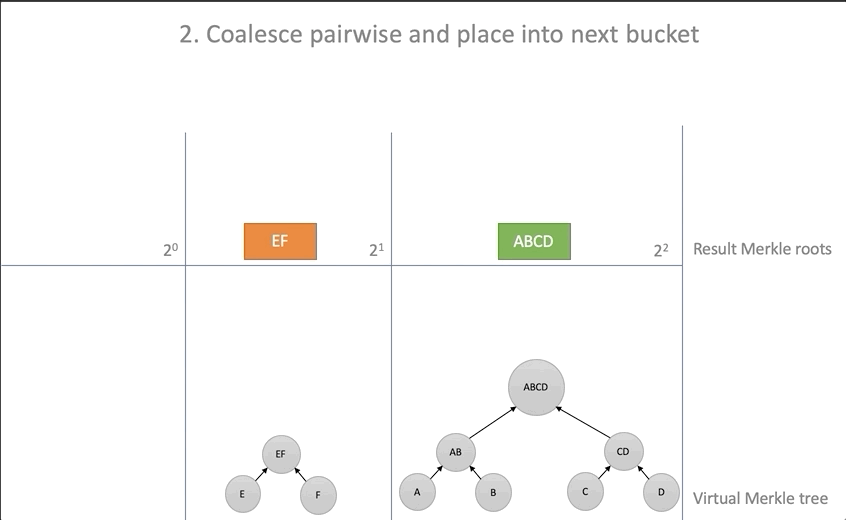
 for i in 0..new_roots.len() { while new_roots[i].len() > 1 { //         let a = new_roots[i][new_roots[i].len() - 2]; let b = new_roots[i][new_roots[i].len() - 1]; new_roots[i].pop(); new_roots[i].pop(); let hash = self.parent(&a, &b); //      if new_roots.len() <= i + 1 { new_roots.push(vec![]); } //      new_roots[i + 1].push(hash); //    ; //        updated.insert(a, ProofStep { hash: b, is_left: false }); updated.insert(b, ProofStep {hash: a, is_left: true }); } } 

• Move the root elements from the baskets to the resulting battery array

 for (i, bucket) in new_roots.into_iter().enumerate() { //     if self.roots.len() <= i { self.roots.push(None); } if bucket.is_empty() { self.roots[i] = None; } else { self.roots[i] = Some(bucket[0]); } } 

Creating evidence for added items

The proof of the inclusion of the element in the battery ( Proof ) will serve as the path Merkle (Merkle Path), consisting of a chain ProofStep . If the path leads nowhere, then the proof is false.

 ///         . #[derive(Debug, Copy, Clone)] pub struct ProofStep { pub hash: Hash, pub is_left: bool, } ///   .       . #[derive(Debug, Clone)] pub struct Proof { pub steps: Vec<ProofStep>, pub leaf: Hash, } 

Using the information obtained earlier in the course of adding an element (structure Update ), you can create evidence that the element was added to the battery. To do this, we go around the table of the changes made and add each step to the path of Merkle, which later will serve as evidence:

 impl<'a> Update<'a> { pub fn prove(&self, leaf: &Hash) -> Proof { let mut proof = Proof { steps: vec![], leaf: *leaf, }; let mut item = *leaf; while let Some(s) = self.updated.get(&item) { proof.steps.push(*s); item = parent(&item, &s); } proof } }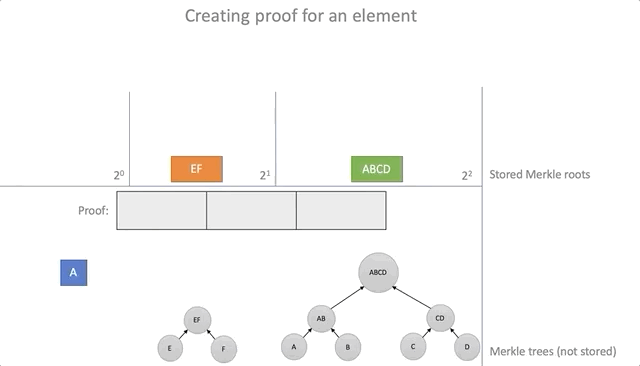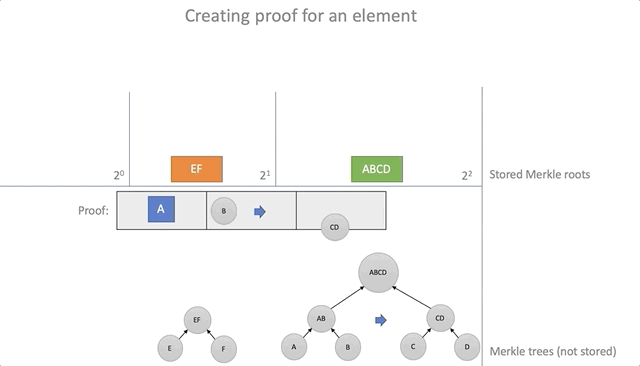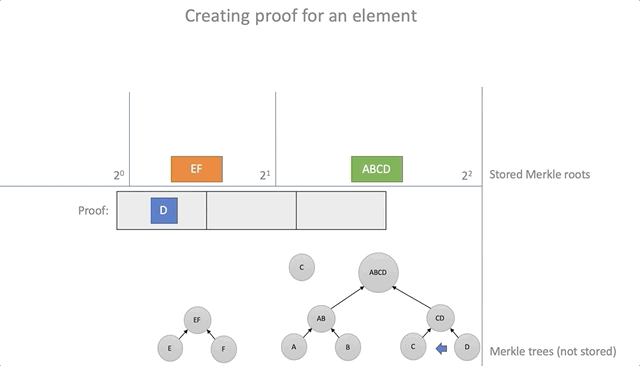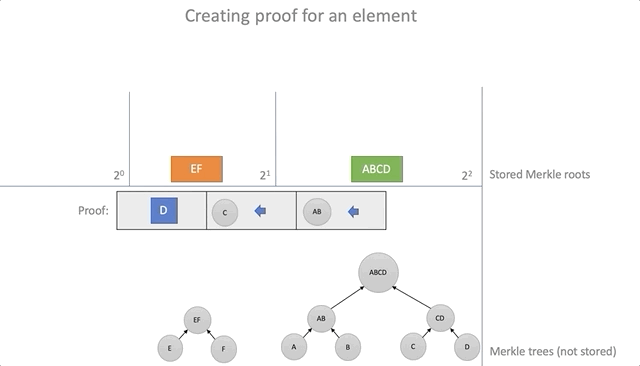 

Proof of evidence for

Testing the proof of inclusion of an element (inclusion proof) is reduced to following the path of Merkle until it leads to the existing root element:

 pub fn verify(&self, proof: &Proof) -> bool { let n = proof.steps.len(); if n >= self.roots.len() { return false; } let expected = self.roots[n]; if let Some(expected) = expected { let mut current_parent = proof.leaf; for s in proof.steps.iter() { current_parent = if s.is_left { parent(&s.hash, &current_parent) } else { parent(&current_parent, &s.hash) }; } current_parent == expected } else { false } } 

Clearly:

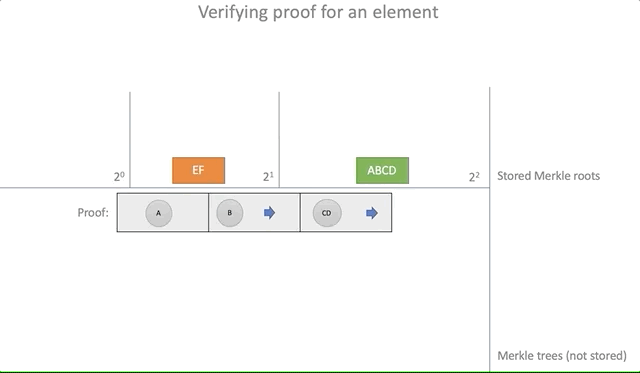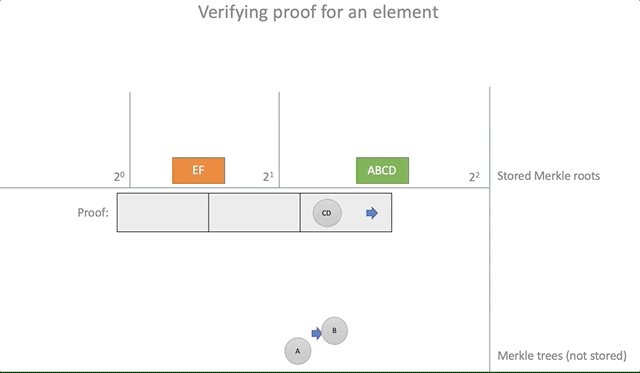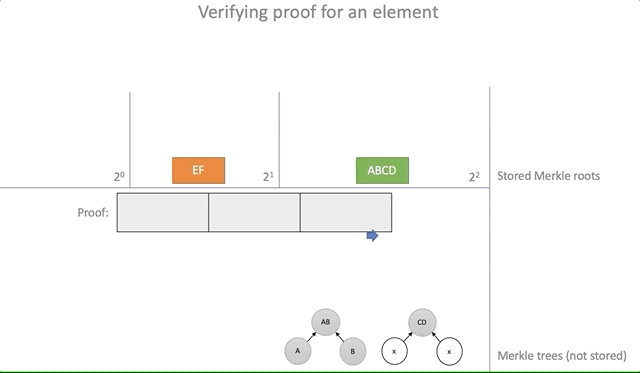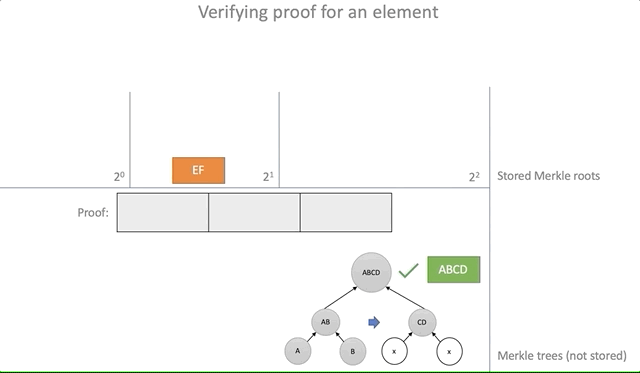
Deleting items

To remove an item from the battery, you need to provide valid proof that the item is there. Using the data from the proof, it is possible to calculate the new root elements of the accumulator for which this proof will no longer be true.

The algorithm is as follows:

1. As with the addition, we will organize a set of empty baskets corresponding to the Merkle trees with a height of equal to two from the basket index
2. Insert items from the steps of the Merkle path into the baskets; the basket index is equal to the current step number
3. Remove the root element, which leads the way from the proof
4. As with the addition, we calculate the new root elements by combining the elements from the baskets in pairs and moving the result of the combination into the next basket.

 fn delete(&self, proof: &Proof, new_roots: &mut Vec<Vec<Hash>>) -> Result<(), ()> { if self.roots.len() < proof.steps.len() || self.roots.get(proof.steps.len()).is_none() { return Err(()); } let mut height = 0; let mut hash = proof.leaf; let mut s; loop { if height < new_roots.len() { let (index, ok) = self.find_root(&hash, &new_roots[height]); if ok { // Remove hash from new_roots new_roots[height].remove(index); loop { if height >= proof.steps.len() { if !self.roots[height] .and_then(|h| Some(h == hash)) .unwrap_or(false) { return Err(()); } return Ok(()); } s = proof.steps[height]; hash = self.parent(&hash, &s); height += 1; } } } if height >= proof.steps.len() { return Err(()); } while height > new_roots.len() { new_roots.push(vec![]); } s = proof.steps[height]; new_roots[height].push(s.hash); hash = self.parent(&hash, &s); height += 1; } } 

The process of removing the element "A":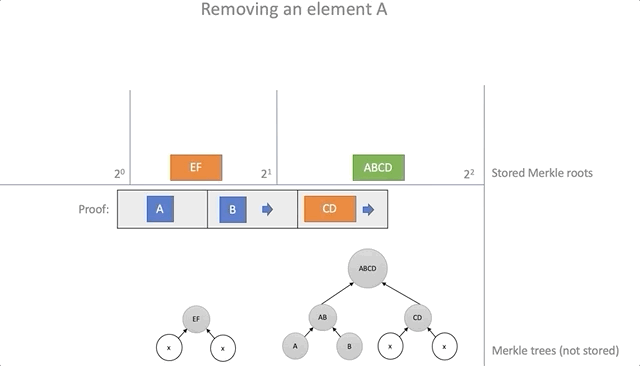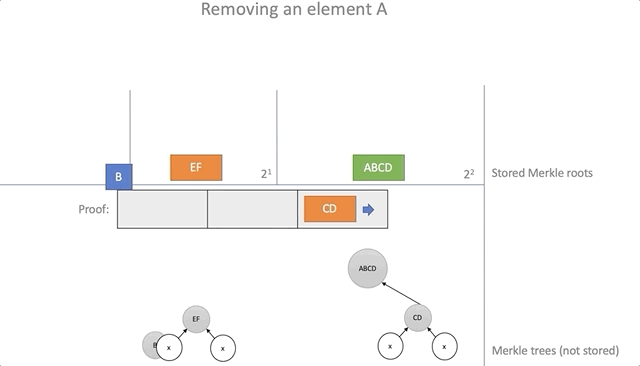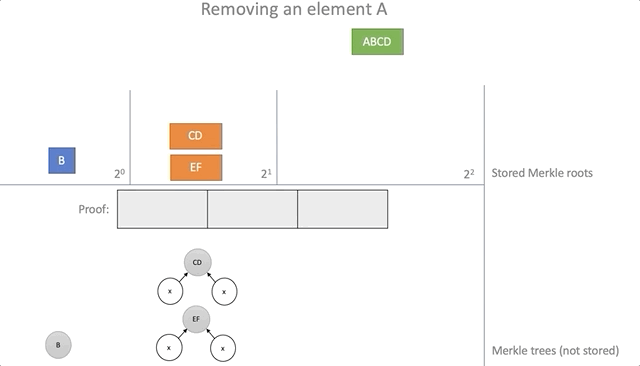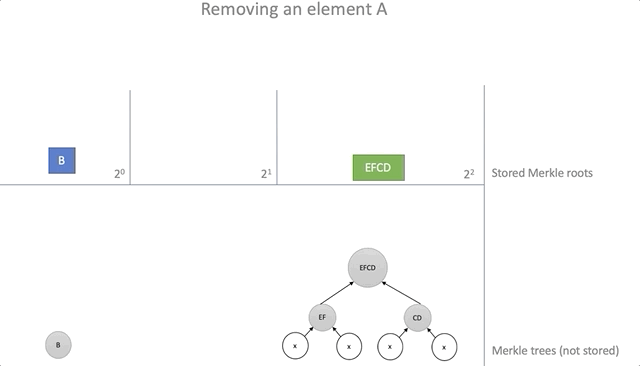

Integration into existing network

Using the proposed battery, the nodes can refuse to use the database to store all UTXO, while maintaining the ability to change the UTXO-set. However, there is the problem of working with evidence.

Let's call a validator node that uses a UTXO battery compact (compact-state node), and a validator without battery - full (full node). The existence of two classes of nodes creates the problem of integrating them into a single network, since compact nodes require proof of the existence of UTXO, which are spent in transactions, and full nodes are not. If all the network nodes do not switch to Utreexo at the same time and in a coordinated manner, then the compact nodes will be left behind and will not be able to work in the Bitcoin network.

To solve the problem of integration of compact nodes in the network, it is proposed to introduce an additional class of nodes - bridges . A bridge node is a complete node that, among other things, stores a Utreexo battery and proof of inclusion for all UTXOs from UTXO-set. Bridges calculate new hashes and update battery and evidence as new blocks arrive with transactions. Support and update of the battery and evidence does not impose additional computational load on such nodes. Bridges sacrifice disk space: order required $$$2n$ hashes compared to $$$log (n)$ hashes for compact nodes, where n is the power of the UTXO set.

Network architecture

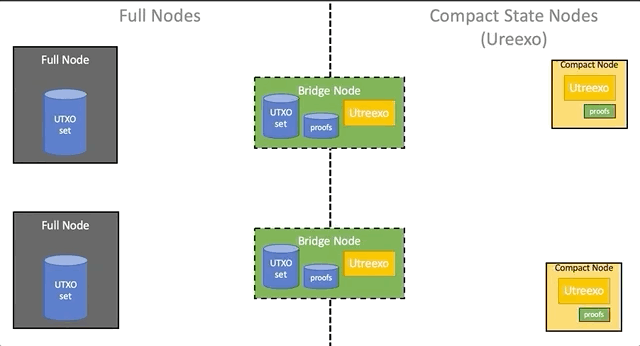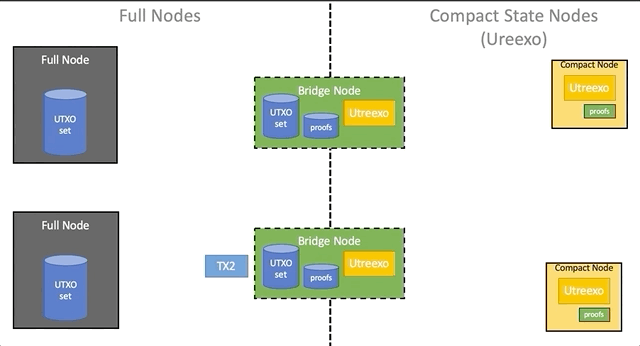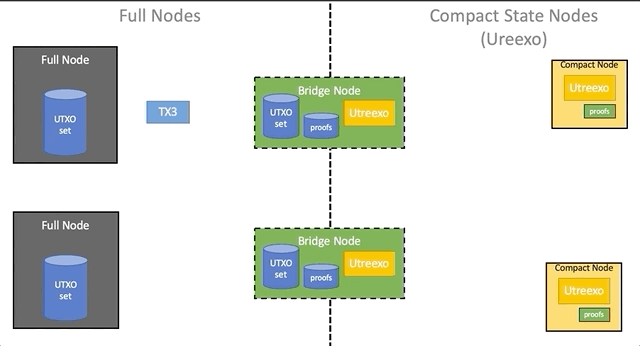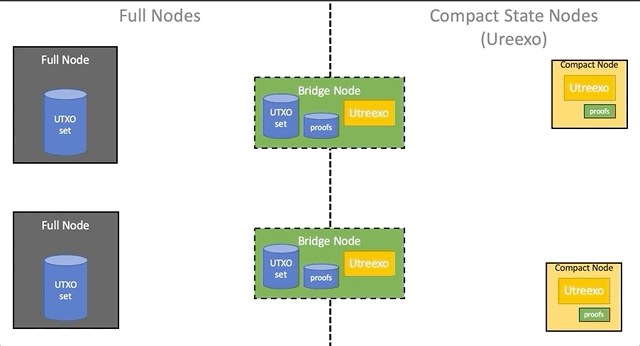
Bridges make it possible to gradually add compact nodes to the network without changing the software of existing nodes. Full nodes work as before, spreading transactions and blocks among themselves. The bridge nodes represent the complete nodes, which additionally store the Utreexo battery data and a set of evidence of inclusion for all UTXOs at the moment. The bridge node does not advertise itself as such, pretending to be a full node for all full nodes and a compact node for all compact ones. Although bridges connect both networks together, in reality you only need to connect them in one direction: from the existing full nodes to the compact nodes. This is possible because the transaction format does not need to be changed, and evidence for UTXO for compact nodes can be discarded, so any compact node can also send transactions to all network participants without the participation of bridge nodes.

Conclusion

We looked at the Utreexo battery and implemented its prototype in Rust. Considered the network architecture, which will integrate nodes based on the battery. The advantage of a compact catch is the size of the stored data, which depends logarithmically on the power of the UTXO set, which greatly reduces the requirements for disk space and storage performance for such nodes. The disadvantage is the additional traffic of nodes for the transfer of evidence, but evidence aggregation techniques (when one evidence proves the existence of several elements) and caching can help keep traffic within acceptable limits.

References :

• Utreexo prototype github on Rust
• Thaddeus Dryja - Utreexo: a dynamic hash-based accumulator optimized for the Bitcoin UTXO set
• Animated illustrations from the article