If you are not writing a program, do not use a programming language.

Leslie Lamport is the author of the basic works in distributed computing, and you can also know him by the letters La in the word La TeX - “Lamport TeX”. It was he who, for the first time, in 1979, introduced the concept of sequential consistency , and his article “How to Make Multiprocess Programs” won the Dijkstra Prize (more precisely, in 2000 the prize was called as before: “PODC Influential Paper Award "). About him there is an article in Wikipedia , where you can get some more interesting links. If you are delighted with the problem-solving of what happens before or the problems of the Byzantine generals (BFT), then you should understand that Lamport is behind all this.

This habrastatia is a translation of the Leslie report at the Heidelberg Laureate Forum in 2018. The report will discuss the formal methods used in the development of complex and critical systems such as the Rosetta space probe or the Amazon Web Services engines. Viewing this report is a must-see for a question and answer session that Leslie will give at the Hydra conference — this habstattya can save you an hour of time watching a video. At this entry is completed, we give the floor to the author.

Once upon a time, Tony Hoar wrote: "In every big program there lives a small program that tries to get out." I would paraphrase it like this: “In every big program there lives an algorithm that is trying to get out”. I don’t know, though, whether Tony agrees with this interpretation.

Consider as an example the Euclidean algorithm for finding the greatest common divisor of two positive integers $$$(M, N)$ . In this algorithm, we assign $$$x$ value $$$M$ , $$$N$ - meaning $$$y$ , and then subtract the smallest of these values ​​from the largest, until they are equal. Value of these $$$x$ and $$$y$ and will be the greatest common divisor. What is the significant difference between this algorithm and the program that implements it? There will be a lot of low-level things in such a program: $$$M$ and $$$N$ there will be a certain type, BigInteger or something like that; it will be necessary to determine the behavior of the program in case $$$M$ and $$$N$ nonpositive; and so on and so forth. There is no clear difference between algorithms and programs, but at the intuitive level we feel the difference - the algorithms are more abstract, higher-level. And, as I said, inside each program there lives an algorithm that is trying to get out. Usually these are not the algorithms that we were told about in the course of algorithms. As a rule, this is an algorithm that is only useful for this particular program. Most often it will be much more difficult than those described in the books. Such algorithms are often called specifications. And in most cases, this algorithm fails to get out, because the programmer is unaware of its existence. The fact is that this algorithm cannot be seen if your thinking is focused on code, on types, exceptions, while loops and so on, and not on the mathematical properties of numbers. A program written in this way is difficult to debug, so what does it mean to debug an algorithm at the code level. Debugging tools are designed to find errors in the code, and not in the algorithm. In addition, such a program will be inefficient, because, again, you will optimize the algorithm at the code level.

As in almost any other field of science and technology, these problems can be solved by describing them mathematically. For this there are many ways, we consider the most useful of them. It works with both sequential and parallel (distributed) algorithms. This method consists in describing the execution of the algorithm as a sequence of states, and each state as the assignment of properties to variables. For example, the Euclidean algorithm is described as a sequence of the following states: first, x is assigned the value M (number 12), and y is the value N (number 18). Then we subtract the smaller value from the larger ( $$$x$ from $$$y$ ), which brings us to the next state, in which we are depriving $$$y$ from $$$x$ , and on this the execution of the algorithm stops: $$$[x \ leftarrow 12, \ leftarrow 18], [x \ leftarrow 12, \ leftarrow 6], [x \ leftarrow 6, \ leftarrow 6]$ .

We call the sequence of states a behavior, and a pair of consecutive states a step. Then any algorithm can be described by a set of behaviors that represent all possible variants of the algorithm. For each concrete M and N there is only one embodiment of execution, therefore for its description the set from one behavior is enough. More complex algorithms, especially parallel ones, have large sets of behaviors.

Many behaviors are described, first, by the initial predicate for states (the predicate is just a function with a boolean value); and, secondly, the predicate of the next state for pairs of states. Some behavior $$$s_1, s_2, s_3 ...$ enters the set of behaviors only if the initial predicate is true for $$$s_1$ and predicates of the next state are true for each step. $$$(s_i, s_ {i + 1})$ . Let's try to describe in this way the Euclidean algorithm. The initial predicate here is: $$$(x = M) \ land (y = N)$ . And the predicate of the next state for pairs of states here is described by the following formula:

Please do not be alarmed - there are only six lines in it, it is very easy to understand them if you do it in order. In this formula, variables without strokes refer to the first state, and variables with strokes are the same variables in the second state.

As you can see, the first line says that in the first case x is greater than y in the first state. After the logical AND, it is stated that the value of x in the second state is equal to the value of x in the first state minus the value of y in the first state. After another logical AND, it is stated that the value of y in the second state is equal to the value of y in the first state. All this means that in the case when x is greater than y, the program will take y from x and leave y unchanged. The last three lines describe the case when y is greater than x. Note that this formula is false if x is equal to y. In this case, there is no next state, and the behavior stops.

So, we just described the Euclidean algorithm with two mathematical formulas - and we did not have to get involved in any programming language. What could be more beautiful than these two formulas? Replace them with one formula. Behavior $$$s_1, s_2, s_3 ...$ is the execution of the Euclidean algorithm only if:

• $$$Init_E$ true for $$$s_1$ ,
• $$$Next_E$ true for every step $$$(s_i, s_ {i + 1})$ .

We can write this as a predicate for behaviors (we will call it a property) as follows. The first condition can be simply expressed as $$$Init_E$ . This means that we interpret a state predicate as valid for behavior only if it is true for the first state. The second condition is written as: $$$\ square Next_E$ . A square means a correspondence between the predicates of pairs of states and the predicates of behavior, that is, $$$Next_E$ true for every step in behavior. As a result, the formula looks like this: $$$Init_E \ land \ square Next_E$ .

So, we wrote down the Euclidean algorithm mathematically. In essence, these are simply definitions, or abbreviations for $$$Init_E$ and $$$Next_E$ . Completely, this formula would look like this:

Isn't she beautiful? Unfortunately, for science and technology, beauty is not the determining criterion, but it says that we are on the right track.

The property we recorded is true for some behavior only if the two conditions that we just described are fulfilled. With $$$M = 12$ and $$$N = 18$ they are correct for the following behavior: $$$[x \ leftarrow 12, \ leftarrow 18], [x \ leftarrow 12, \ leftarrow 6], [x \ leftarrow 6, \ leftarrow 6]$ . But these conditions are also satisfied for shorter versions of the same behavior: $$$[x \ leftarrow 12, \ leftarrow 18], [x \ leftarrow 12, \ leftarrow 6]$ . And we should not take them into account, since these are just separate steps of the behavior we already take into account. There is an obvious way to get rid of them: just ignore behaviors that end in a state for which at least one next step is possible. But this is not quite the right approach, we need a more general solution. In addition, this condition does not always work.

Discussion of this problem leads us to the concepts of security and activity. The security property indicates which events are valid. For example, the algorithm is allowed to return the correct value. The activity property indicates which events should occur sooner or later. For example, the algorithm should return some value sooner or later. For the Euclidean algorithm, the security property is as follows: $$$Init_E \ land \ square Next_E$ . To this must be added the property of activity in order to exclude premature stops: $$$Init_E \ land \ square Next_E \ land L$ . In programming languages, at best, there is some primitive definition of activity. Most often, the activity is not even mentioned, it simply means that the next step in the program must occur. And to add this property, you need a rather intricate code. Mathematically, the activity is very easy to express (just this box is needed for this), but, unfortunately, I don’t have time for that - we will have to limit our discussion to security.

A small digression only for mathematicians: each property is a set of behaviors for which this property is true. For each set of sequences, there is a natural topology that the following distance function creates:

$$$s = 17, \ sqrt {2}, -2, \ pi, 10, 1/2 \\ t = 17, \ sqrt {2}, -2, e, 10, 1/2$

The distance between these two functions is ¼, since the first difference between them is on the fourth element. Accordingly, the longer the section in which these sequences are identical, the closer they are to each other. By itself, this function is not so interesting, but it creates a very interesting topology. In this topology, security properties are closed sets, and activity properties are dense sets. In topology, one of the fundamental theorems says that each set is the intersection of a closed set and a dense set. If we recall that properties are sets of behaviors, it follows from this theorem that each property is a conjunction of a safety property and an activity property. This is a conclusion that will be interesting including to programmers.

Partial correctness means that the program can only stop if it gives the correct answer. The partial correctness of the Euclidean algorithm states that if it has completed execution, then $$$x = GCD (M, N)$ . A completes the execution of our algorithm in case $$$x = y$ . In other words, $$$(x = y) \ Rightarrow (x = GCD (M, N))$ . Partial correctness of this algorithm means that this formula is true for all states of behavior. Add a symbol to its beginning $$$\ square$ which means "for all steps." As we see, in the formula there are no variables with a prime, so that its truth depends on the first state at each step. And if something is true for the first state of each step, then this statement is true for all states. The partial correctness of the Euclidean algorithm is satisfied by any behavior that is valid for the algorithm. As we have seen, behavior is permissible if the formula just given is true. When we say that a property is satisfied, it simply means that this property follows from some formula. Isn't it beautiful? Here she is:

$$$Init_E \ land \ square Next_E \ Rightarrow \ square ((x = y) \ Rightarrow (x = GCD (M, N)))$

Let us turn to invariance. The square with the brackets after it is called the invariance property :

$$$Init_E \ land \ square Next_E \ Rightarrow \ color {red} {\ square ((x = y) \ Rightarrow (x = GCD (M, N)))}$

The value enclosed in brackets after the square is called the invariant :

$$$Init_E \ land \ square Next_E \ Rightarrow \ square (\ color {red} {(x = y) \ Rightarrow (x = GCD (M, N))})$

How to prove invariance? To prove $$$Init_E \ land \ square Next_E \ Rightarrow \ square I_E$ , you need to prove that for any behavior $$$s_1, s_2, s_3 ...$ consequence $$$Init_E \ land \ square Next_E$ is the truth $$$I_E$ for any condition $$$s_j$ . We can prove it by induction, for this we need to prove the following:

1. of $$$Init_E \ land \ square Next_E$ follows that $$$I_E$ true to state $$$s_1$ ;
2. of $$$Init_E \ land \ square Next_E$ it follows that if $$$I_E$ true to state $$$s_j$ then it also
   true to state $$$s_ {j + 1}$ .

First you need to prove that $$$Init_E$ implies $$$I_E$ . Since the formula states that $$$Init_E$ true for the first state, it means that $$$I_E$ true for the first state. Further, when $$$Next_E$ , true to any step, and $$$I_E$ true to $$$s_j$ , $$$I_E$ true for $$$s_ {j + 1}$ , because $$$\ square Next_E$ means what $$$Next_E$ true for any pair of states. This is written like this: $$$Next_E \ land I_E \ Rightarrow I'_E$ where $$$I'_E$ - this $$$I_E$ for all variables with a stroke.

An invariant that meets the two conditions that we have just proved is called an inductive invariant . Partial correctness is not inductive. To prove its invariance, you need to find an inductive invariant that implies it. In our case, the inductive invariant will be: $$$GCD (x, y) = GCD (M, N)$ .

Each subsequent action of the algorithm depends on its current state, and not on past actions. The algorithm satisfies the security property, since the inductive invariant is preserved in it. The Euclidean algorithm can calculate the greatest common denominator (i.e., it does not stop until it reaches), due to the fact that it has an invariant $$$GCD (x, y) = GCD (M, N)$ . To understand an algorithm, you need to know its inductive invariant. If you studied the verification of programs, then you know that the proof just presented for the invariant is nothing more than a method for proving that Floyd-Hoare sequential programs are partially correct. You may also have heard about the Hoviki - Gries method , which is a distribution of the Floyd-Hoare method to parallel programs. In both cases, the inductive invariant is written using the program annotation. And if it is done with the help of mathematics, and not a programming language, it is done very simply. This is the basis of the Hoviki-Green method. Mathematics makes complex phenomena much more accessible to understanding, although the phenomena themselves, of course, will not make this easier.

Take a closer look at the formulas. If in math we wrote a formula with variables $$$x$ and $$$y$ This does not mean that other variables do not exist. You can add another equation in which $$$y$ delivered in relation to $$$z$ it will not change anything. Just the formula says nothing about any other variables. I have already said that the state is the assignment of values ​​to variables, now we can add to this: all possible variables, starting $$$x$ and $$$y$ and ending with the population of Iran. I must confess: when I said that the formula $$$Init_E \ land \ square Next_E$ describes the Euclidean algorithm, I lied. In fact, it describes a universe in which the meanings $$$x$ and $$$y$ represent the execution of the Euclidean algorithm. The second part of the formula ( $$$\ square Next_E$ a) asserts that every step changes $$$x$ or $$$y$ . In other words, it describes a universe in which the population of Iran can only change if the value of $$$x$ or $$$y$ . From this it follows that no one in Iran can be born after the execution of the Euclidean algorithm is completed. Obviously, this is not the case. It is possible to correct this error if we have valid steps for which $$$x$ and $$$y$ remain unchanged. Therefore, we need to add one more part to our formula: $$$Init_E \ land \ square (Next_E \ lor (x '= x) \ land (y' = y))$ . For brevity, write it like this: $$$Init_E \ land \ square [Next_E] _ {<x, y>}$ . This formula describes the universe containing the Euclidean algorithm. The same changes need to be made in the proof of the invariant:

• We prove: $$$Init_E \ land \ color {red} {\ square [Next_E] _ {<x, y>}} \ Rightarrow \ square I_E$
• Via:
  
  1. $$$Init_E \ Rightarrow I_E$
  2. $$$\ color {red} {\ square [Next_E] _ {<x, y>}} \ land I_E \ Rightarrow I'_E$

This change is responsible for the security of the Euclidean algorithm, since behaviors in which the values $$$x$ and $$$y$ do not change. Eliminate such behaviors with the help of the activity property. It is quite simple to do this, but now I will not talk about it.

Let's talk about the implementation. Suppose we have some machine that implements the Euclidean algorithm like a computer. It represents numbers as arrays of 32-bit words. For simple addition and subtraction operations, she needs a lot of steps, like a computer. If we don’t touch the activity so far, then we can also imagine such a machine $$$Init_ {ME} \ land \ square [Next_ {ME}] _ {<...>}$ . What do we mean when we say that the Euclidean machine implements the Euclidean algorithm? This means that the following formula is true:

Do not worry, we will now consider it in order. It says that our car satisfies a certain property ( $$$\ Rightarrow$ ). This property is the Euclidean formula $$$(Init_E \ land \ square [Next_E] _ {<x, y>}$ , dots are expressions that contain Euclidean machine variables, and $$$WITH$ - this is a substitution. In other words, the second line is the Euclidean formula, in which $$$x$ and $$$y$ replaced by expressions in dots. In mathematics, there is no generally accepted notation for substitutions, so I had to invent it myself. Essentially, the Euclidean formula ( $$$Init_E \ land \ square [Next_E] _ {<x, y>}$ ) Is the abbreviation for the formula:

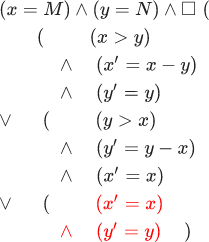
Red highlights the part of the formula that allows $$$x$ and $$$y$ at $$$(Init_E \ land \ square [Next_E] _ {\ color {red} {<x, y>}}$ remain unchanged.

The described expression asserts not only that the machine implements the Euclidean algorithm, but also that it does so taking into account the indicated substitutions. If you just take a couple of programs and say that the variables of these programs are related to $$$x$ and $$$y$ - it makes no sense to say that all this "implements the Euclidean algorithm". It is necessary to indicate exactly how the algorithm will be implemented, why after all substitutions the formula will become true. Now I don’t have time to show that the above definition is correct, you have to take my word for it. But you, I think, have already appreciated how simple and elegant it is. Mathematics is really beautiful - with the help of it we were able to determine what it means that one algorithm implements the other.

To prove this, you need to find a suitable invariant. $$$I_ {ME}$ Euclid's cars. To do this, you must fulfill the following conditions:

1. $$$Init_ {ME} \ Rightarrow (Init_E, WITH \ thinspace x \ leftarrow ..., y \ leftarrow ...)$
2. $$$I_ {ME} \ land [Next_ {ME}] _ {<...>} \ Rightarrow ([Next_E] _ {<x, y>}, WITH \ thinspace x \ leftarrow ..., y \ leftarrow. ..)$

We will not delve into them now, just pay attention to the fact that these are ordinary mathematical formulas, although they are not the simplest. Invariant $$$I_ {ME}$ explains why the Euclidean machine implements the Euclidean algorithm. Realization means the substitution of expressions in place of variables. This is quite a common mathematical operation. But in the program such substitution is impossible to perform. It is impossible to substitute a + b in place of x in the assignment expression x = … , such a record would not make sense. Then how to determine that one program implements another? If you think only in terms of programming - this is impossible. At best, you can find some clever definition, but a much better way is to translate programs into mathematical formulas and use the definition that I gave above. To translate a program into a mathematical formula means to give the program semantics. If the Euclidean machine is a program, $$$Init_ {ME} \ land \ square [Next_ {ME}] _ {<...>}$ - her mathematical notation, then $$$(Init_E \ land \ square [Next_E] _ {<x, y>}, WITH \ thinspace x \ leftarrow ..., y \ leftarrow ...)$ shows us that this means that “the program implements the Euclidean algorithm”. Programming languages ​​are very complex, so this translation of the program into the language of mathematics is also complex, so in practice we do not do that. Simply programming languages ​​are not intended to write algorithms on them. , , , : , x y , . , , , .

- : , , , . , . — . . , . , — , . :

. $$$DecrementX$ :

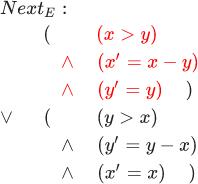
— $$$DecrementY$ :

, :

.

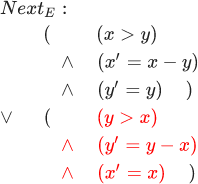
. Rosetta — , . Virtuoso. . TLA+, . , , . , (Eric Verhulst), . , TLA+, : « TLA+ . - C. TLA+ Virtuoso». . . , , , . . TLA+. , .

. Communications of the ACM ] , - Amazon . Amazon Web Services — , Amazon. , — TLA+. . -, , . , , . -, , . , — , , . -, , Amazon , . , 10% TLA+.

— Microsoft. TLA+ 2004 . 2015 TLA+, . . Amazon Web Services. Microsoft , , . : « , ». , Microsoft - . : « ». 2016-17 . TLA+, 150 , Azure ( Microsoft). Azure 2018 , , . : « , . , ». , , . - : , . , , .

, TLA+ . , TLA+, TLA+ Azure, , TLA+. , . , TLA+ , . Microsoft Cosmos DB, , . , . TLA+, , , TLA+.

TLA+ — . . TLA+ . , , . TLA+ , . : TLA+ , .

, . , , . , . Amazon Microsoft , . , .

, . — , . , Hydra 2019, 11-12 2019 -. .