Merkle Tree: rusty and fast
Hello! Recently discovered the language of Rust. He shared his first impressions in a previous article . Now I decided to dig a little deeper, this requires something more serious than the list. My choice fell on the tree Merkle. In this article I want:
- tell about this data structure
- look at what is already in Rust
- offer your implementation
- compare performance
Merkle tree
This is a relatively simple data structure, and there is already a lot of information about it on the Internet, but I think my article will be incomplete without a description of the tree.
What is the problem
The Merkle tree was invented back in 1979, but gained its popularity thanks to the blockchain. The chain of blocks in the network has a very large size (for bitcoin it is more than 200 GB), and not all nodes can deflate it. For example, telephones or cash registers. However, they need to be aware of the fact that a transaction has been included in the block. For this, the protocol SPV - Simplified Payment Verification was invented.
How the tree works
This is a binary tree whose leaves are the hashes of any objects. To build the next level, the hashes of neighboring leaves are taken in pairs, concatenated, and the hash from the result of the concatenation is calculated, which is illustrated in the picture in the header. Thus, the root of the tree is a hash of all leaves. If you remove or add an element, the root will change.
How the tree works
With the Merkle tree, you can build evidence that the transaction is included in the block as a path from the transaction hash to the root. For example, we are interested in the Tx2 transaction, for which the proof will be (Hash3, Hash01). This mechanism is used in SPV. The client extorts only the block header with its hash. Having a transaction of interest, he asks for proof from the node containing the entire chain. Then does the check for Tx2 it will be:
hash(Hash01, hash(Hash2, Hash3)) = Root Hash The result obtained is compared with the root of the block header. This approach makes it impossible to fake evidence, since in this case the result of the test will not converge with the contents of the header.
What are already implemented
Rust is a young language, but many implementations of the Merkle tree are already written on it. Judging by Github, at the moment 56, this is more than C and C ++ combined. Although Go makes them stand up with 80 implementations.
SpinResearch / merkle.rs
For my comparison, I chose this implementation by the number of stars in the repository.
This tree is constructed in the most obvious way, that is, it is a graph of objects. As I have already noted, this approach is not quite Rust-friendly. For example, it is impossible to make bidirectional communication from children to parents.
The construction of the proof occurs through the search in depth. If the sheet with the desired hash is found, then the path to it will be the result.
What can be improved
It was just not interesting for me to do the (n + 1) th implementation, so I thought about optimization. The code for my vector-merkle-tree is on Github .
Data storage
The first thing that comes to mind is to shift the tree to an array. This solution will be much better in terms of data locality: more cache hits and better preloading. Traversing objects scattered in memory takes longer. A convenient fact is that all hashes have the same length, since calculated by one algorithm. The Merkle tree in the array will look like this:
Evidence
When initializing a tree, you can create a HashMap with indices of all leaves. Thus, when there is no sheet, it is not necessary to bypass the whole tree, and if there is, then you can immediately go to it and rise to the root, building a proof. In my implementation, I made HashMap optional.
Concatenation and hashing
It would seem that there can be improved? Everything is clear, we take two hashes, glue them together and calculate the new hash. But the fact is that this function is non-commutative, i.e. hash (H0, H1) ≠ hash (H1, H0). Because of this, when constructing evidence, it is necessary to memorize which side the adjacent node is located. This makes the algorithm harder to implement, and adds the need to store extra data. Everything is very easy to fix, just sort the two nodes before hashing. For example, I cited Tx2, with regard to commutativity, the test will look like this:
hash(hash(Hash2, Hash3), Hash01) = Root Hash When you don’t need to take care of the order, the check algorithm looks like a simple convolution of an array:
pub fn validate(&self, proof: &Vec<&[u8]>) -> bool { proof[2..].iter() .fold( get_pair_hash(proof[0], proof[1], self.algo), |a, b| get_pair_hash(a.as_ref(), b, self.algo) ).as_ref() == self.get_root() } The zero element is the hash of the desired object, the first is its neighbor.
Let's go!
The story would be incomplete without a performance comparison, which took me several times longer than the implementation of the tree itself. For these purposes, I used the criterion framework. The sources of the tests themselves are here . All testing takes place through the TreeWrapper interface, which was implemented for both experimental:
pub trait TreeWrapper<V> { fn create(&self, c: &mut Criterion, counts: Vec<usize>, data: Vec<Vec<V>>, title: String); fn find(&self, c: &mut Criterion, counts: Vec<usize>, data: Vec<Vec<V>>, title: String); fn validate(&self, c: &mut Criterion, counts: Vec<usize>, data: Vec<Vec<V>>, title: String); } Both trees work with the same ring cryptography. Here I am not going to compare different libraries. Took the most common.
Randomly generated strings are used as hashing objects. Trees are compared on arrays of various lengths: (500, 1000, 1500, 2000, 2500 3000). 2500 - 3000 is the approximate number of transactions in the bitcoin block at the moment.
On all graphs on the X axis - the number of elements of the array (or the number of transactions in the block), Y - the average time to perform the operation in microseconds. That is, the more, the worse.
Tree creation
Storing all tree data in a single array greatly exceeds the performance of object graphs. For an array with 500 elements 1.5 times, and for 3000 elements already 3.6 times. The nonlinear nature of the dependence of complexity on the volume of input data in the standard implementation is clearly visible.
Also in comparison, I added two variants of a vector tree: with and without HashMap . Filling an additional data structure adds about 20%, but it allows you to search for objects much faster when constructing a proof.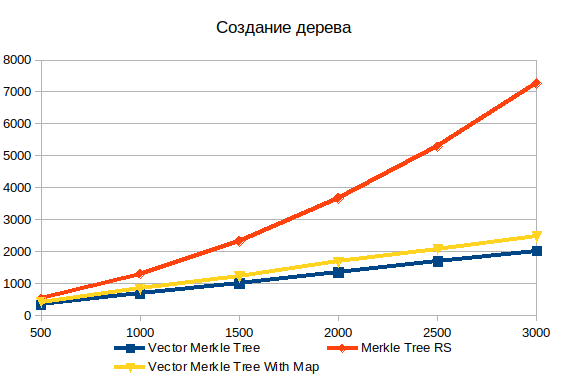
Building evidence
Here is the apparent inefficiency of the search in depth. With the increase in input data, it only gets worse. It is important to understand that the required objects are sheets, so the complexity of log (n) cannot be. If the data is pre-hashed, the operation time is practically independent of the number of elements. Without hashing, complexity grows linearly and consists in searching through brute force.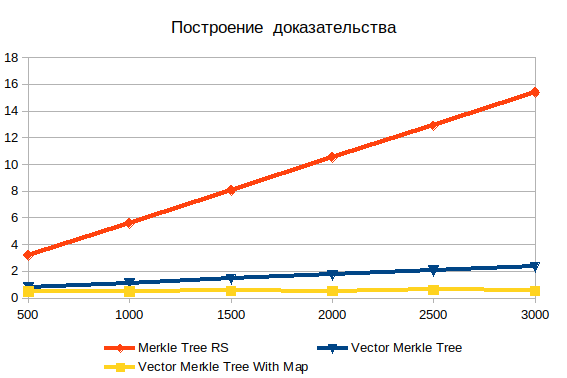
Validation of evidence
This is the last operation. It does not depend on the structure of the tree, because works with the result of constructing evidence. I believe that the main difficulty here is the calculation of the hash.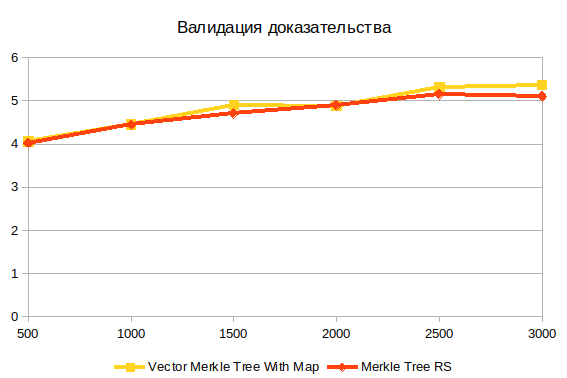
Total
- The way data is stored greatly affects performance. When everything is in one array, it is much faster. And it will be very easy to serialize such a structure. The total amount of code is also reduced.
- Concatenating nodes with sorting greatly simplifies the code, but does not make it faster.
A little about Rust
- Like the criterion framework. Produces clear results with averages and deviations complete with graphs. Able to compare different implementations of the same code.
- Lack of inheritance does not interfere with life.
- Macros - a powerful mechanism. I used them in tests of my tree for parameterization. I think if you use them badly, you can do this, that you will not be happy then.
- Mostly the compiler tired of its memory checks. My initial assumption that starting so simply by writing on Rust did not work out was true.
Links
')
Source: https://habr.com/ru/post/455260/
All Articles