Programming is more than coding

This article is a translation of the Stanford workshop . But before her a small entry. How are zombies formed? Everyone got into a situation when they want to pull a friend or colleague up to their level, but it does not work. Moreover, “it does not work out” not so much with you, as with him: on one side of the scale there is a normal salary, tasks and so on, and on the other - the need to think. Thinking is unpleasant and painful. He quickly gives up and continues to write code, completely without including the brain. You can imagine how much effort you need to spend to overcome the barrier of learned helplessness, and you simply do not do it. This is how zombies are formed, which seem to be cured, but no one seems to be doing this either.

When I saw that Leslie Lamport (yes, that very comrade of textbooks) was coming to Russia and was not making a report, but a question-and-answer session, I was wary of a bit. Just in case, Leslie is a world-renowned scientist, the author of fundamental works in distributed computing, and you can also know him by the letters La in the word LaTeX - “Lamport TeX”. The second alarming factor is his demand: everyone who comes must (absolutely for free) listen in advance to a couple of his reports, come up with at least one question on them and only then come. I decided to see what Lamport is saying there - and this is great! That is exactly the thing, the magic reference tablet for treating zombies. I warn you: from the text can significantly burn in lovers of super-flexible methodologies and nonlovers to test writing.

After Habrokat, in fact, the translation of the seminar begins. Enjoy reading!

Whatever task you undertake, you always need to go through three steps:

• decide what goal you want to achieve;
• decide exactly how you will achieve your goal;
• come to your goal.

This also applies to programming. When we write code, we need to:

• decide what the program should do;
• determine exactly how it should perform its task;
• write the appropriate code.

The last step, of course, is very important, but I will not talk about it today. Instead, we discuss the first two. Each programmer executes them before starting work. You do not sit down to write if you have not decided what you are writing: a browser or a database. A certain idea of ​​the goal must be present. And you always think over what exactly the program will do, and do not write somehow in the hope that the code itself will somehow turn into a browser.

How exactly does this preliminary code thinking? How much effort should we spend on it? It all depends on how difficult the problem we solve. Suppose we want to write a fault-tolerant distributed system. In this case, we should think about everything properly before sitting behind the code. And if we just need to increase the integer variable by 1? At first glance, everything is trivial here, and no thinking is needed, but then we recall that an overflow may occur. Therefore, even in order to understand whether a problem is simple or complex, one must first think.

If you first think about possible solutions to the problem, you can avoid mistakes. But for this you need your thinking to be clear. To achieve this, you need to write down your thoughts. I really like Dick Gindon's quote: “When you write, nature shows you how untidy your thinking is.” If you do not write, it only seems to you that you are thinking. And you need to write down your thoughts in the form of specifications.

Specifications perform many functions, especially in large projects. But I will only talk about one of them: they help us to think clearly. Clear thinking is very important and quite difficult, so here we need any help. What language should we write the specifications in? In general, this is always the first question for programmers: in what language we will write. There is no one right answer to it: the problems that we solve are too diverse. For some, TLA + is a specification language that I developed. For others, it is more convenient to use Chinese. It all depends on the situation.

Another question is more important: how to achieve clearer thinking? Answer: we must think like scientists. This is a way of thinking that has proven itself well over the past 500 years. In science, we build mathematical models of reality. Astronomy was probably the first science in the strict sense of the word. In the mathematical model used in astronomy, celestial bodies appear as points with mass, position and momentum, although in reality they are extremely complex objects with mountains and oceans, ebbs and flows. This model, like any other, was created to solve certain problems. It is great for determining where to send a telescope if you need to find a planet. But if you want to predict the weather on this planet, this model will not work.

Mathematics allows us to determine the properties of the model. And science shows how these properties relate to reality. Let's talk about our science, computer science. The reality with which we work is computing systems of various types: processors, game consoles, computers, executing programs, and so on. I will talk about the execution of the program on the computer, but, by and large, all these conclusions apply to any computer system. In our science, we use many different models: the Turing machine, partially ordered sets of events, and many others.

What is a program? This is any code that can be considered independently. Suppose we need to write a browser. We perform three tasks: we design the presentation of the program for the user, then we write the high-level scheme of the program, and, finally, we write the code. In the course of writing code, we understand that we need to write a tool for formatting text. Here again we need to solve three problems: to determine what text this tool will return; select an algorithm for formatting; write code. This task has its own subtask: correctly insert a hyphen in the words. We also solve this subtask in three steps - as we see, they are repeated on many levels.

Let us consider in more detail the first step: what problem the program solves. Here we most often model a program as a function that receives some input data and gives some output data. In mathematics, a function is usually described as an ordered set of pairs. For example, the squaring function for natural numbers is described as a set {<0,0>, <1,1>, <2,4>, <3,9>, ...}. The domain of such a function is the set of the first elements of each pair, that is, natural numbers. To define a function, we need to specify its scope and formula.

But functions in mathematics are not the same as functions in programming languages. Math is much simpler. Since I have no time for complex examples, consider a simple one: a function in C or a static method in Java that returns the greatest common divisor of two integers. In the specification of this method, we write: calculates GCD(M,N) for the arguments M and N , where GCD(M,N) is the function whose domain is the set of pairs of integers, and the return value is the largest integer divided by M and N How does reality relate to this model? The model operates with integers, and in C or Java we have a 32-bit int . This model allows us to decide if the GCD algorithm is correct, but it does not prevent an overflow error. This would require a more complex model for which there is no time.

Let's talk about the limitations of the function as a model. The work of some programs (for example, operating systems) is not limited to returning a specific value for certain arguments, they can be performed continuously. In addition, the function as a model is poorly suited for the second step: planning the way to solve the problem. Quick sorting and bubble sorting compute the same function, but these are completely different algorithms. Therefore, to describe how to achieve the goal of the program, I use a different model, let's call it the standard behavioral model. The program in it is represented as the set of all permissible behaviors, each of which, in turn, is a sequence of states, and the state is the assignment of values ​​to variables.

Let's see what the second step will look like for the Euclidean algorithm. We need to calculate GCD(M, N) . We initialize M as x , and N as y , then retake the smaller of these variables from the larger one until they are equal. For example, if M = 12 and N = 18 , we can describe the following behavior:

[x = 12, y = 18] → [x = 12, y = 6] → [x = 6, y = 6]

And if M = 0 and N = 0 ? Zero is divided into all numbers, so the greatest divisor in this case is not. In this situation, we need to go back to the first step and ask: do we really need to calculate the GCD for non-positive numbers? If this is not necessary, then you just need to change the specification.

Here we should make a small digression about productivity. It is often measured in the number of lines of code written per day. But your work is much more useful if you get rid of a certain number of lines, because you have less space for bugs. And the easiest way to get rid of the code is in the first step. It is possible that you simply do not need all the bells and whistles that you are trying to implement. The fastest way to simplify a program and save time is not to do things you should not do. The second step is second in potential to save time. If you measure productivity in the number of written lines, thinking through the way to perform the task will make you less productive , since you can solve the same problem with a smaller amount of code. I can’t give exact statistics here, because I don’t have a way to count the number of lines that I didn’t write because I spent the time on the specification, that is, on the first and second steps. And the experiment here is also not set, because in the experiment we do not have the right to perform the first step, the task is determined in advance.

In informal specifications, it is easy to ignore many difficulties. There is nothing difficult in writing strict specifications for functions; I will not discuss this. Instead, we'll talk about writing strict specifications for standard behavioral models. There is a theorem that states that any set of behaviors can be described using the safety property and the liveness property . Security means that nothing bad will happen, the program will not give the wrong answer. Vitality means that sooner or later something good will happen, that is, the program will sooner or later give the correct answer. As a rule, security is a more important indicator, errors often occur here. Therefore, to save time, I will not talk about survivability, although it is, of course, also important.

We achieve security by prescribing, firstly, the set of possible initial states. And, secondly, the relationship with all possible following states for each state. We will behave as scientists and determine the state mathematically. The set of initial states is described by the formula, for example, in the case of the Euclidean algorithm: (x = M) ∧ (y = N) . For certain values ​​of M and N there is only one initial state. The relationship with the next state is described by a formula in which the variables of the next state are written with a stroke, and the current state is written without a stroke. In the case of the Euclidean algorithm, we will deal with the disjunction of two formulas, in one of which x is the largest value and in the second - y :

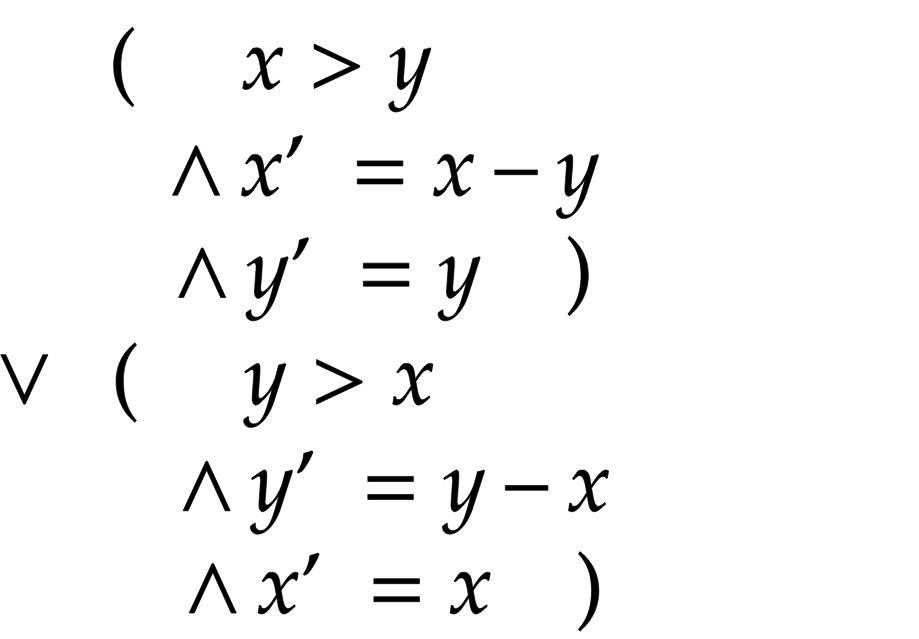
In the first case, the new value of y is equal to the former value of y, and we get the new value of x, taking the smaller variable from the larger variable. In the second case, we do the opposite.

Let's return to the Euclidean algorithm. Suppose again that M = 12 , N = 18 . This defines a single initial state, (x = 12) ∧ (y = 18) . Then we substitute these values ​​into the formula above and we get:

Here the only possible solution is: x' = 18 - 12 ∧ y' = 12 , and we get the behavior: [x = 12, y = 18] . In the same way, we can describe all the states in our behavior: [x = 12, y = 18] → [x = 12, y = 6] → [x = 6, y = 6] .

In the last state [x = 6, y = 6] both parts of the expression will be false, therefore, it does not have the next state. So, we have the complete specification of the second step - as we see, this is quite ordinary mathematics, as in engineers and scientists, and not strange, as in computer science.

These two formulas can be combined into one formula of temporal logic. She is elegant and easy to explain, but there is no time for her now. We may need temporal logic only for the property of liveliness, for safety it is not needed. Temporal logic doesn’t like per se, it’s not quite ordinary mathematics, but in the case of liveliness it is a necessary evil.

In the Euclidean algorithm, for each value of x and y there are unique values ​​of x' and y' , which make the relationship with the next state true. In other words, the Euclidean algorithm is deterministic. To model a non-deterministic algorithm, it is necessary that the current state has several possible future states, and that each value of a variable without a prime has several values ​​of a variable with a stroke, in which the relation with the next state is true. It is easy to do, but now I will not give examples.

To make a working tool, you need formal mathematics. How to make a specification formal? For this we need a formal language, for example, TLA + . The specification of the Euclidean algorithm in this language will be as follows:

The symbol of an equals sign with a triangle means that the value to the left of the sign is defined as equal to the value to the right of the sign. In essence, a specification is a definition, in our case two definitions. To the specification in TLA + you need to add declarations and some syntax, as in the slide above. In ASCII, it will look like this:

As you can see, nothing complicated. The specification for TLA + can be checked, i.e. bypass all possible behaviors in a small model. In our case, this model will be certain values ​​of M and N This is a very effective and easy way to check, which is entirely performed automatically. In addition, you can write a formal proof of truth and check them mechanically, but it takes a lot of time, so almost no one does.

The main disadvantage of TLA + is that it is math, and programmers and computer scientists are afraid of mathematics. At first glance, this sounds like a joke, but, unfortunately, I say this in all seriousness. My colleague just told me how he tried to explain TLA + to several developers. As soon as the formulas appeared on the screen, they immediately had glass eyes. So if TLA + is scary, PlusCal can be used, it's a kind of toy programming language. The PlusCal expression can be any TLA + expression, that is, by and large, any mathematical expression. PlusCal also has syntax for non-deterministic algorithms. Due to the fact that PlusCal can write any TLA + expression, it is much more expressive of any real programming language. Further, PlusCal is compiled into an easily readable TLA + specification. This does not mean, of course, that the PlusCal complex specification will turn into a simple one on TLA + - just the correspondence between them is obvious, there will be no additional complexity. Finally, this specification can be verified with TLA + tools. In general, PlusCal can help overcome the phobia of mathematics, it is easy to understand even for programmers and computer scientists. In the past, I have been posting algorithms on it for some time (about 10 years).

Perhaps someone will argue that TLA + and PlusCal is mathematics, and mathematics only works on invented examples. In practice, we need a real language with types, procedures, objects, and so on. This is not true. Here is what Chris Newcomb, who worked at Amazon, writes: “We used TLA + in ten large projects, and in each case its use made a significant contribution to the development, because we were able to catch dangerous bugs before getting into production, and because he gave us understanding and confidence required for aggressive performance optimizations that do not affect the truth of the program . ” You can often hear that when using formal methods we get an inefficient code - in practice everything is exactly the opposite. In addition, there is a perception that managers cannot be convinced of the need for formal methods, even if programmers are convinced of their usefulness. And Newcomb writes: "Managers are now strongly urging them to write specifications for TLA +, and they specifically set aside time for this . " So when managers see that TLA + works, they gladly accept it. Chris Newcomb wrote this about six months ago (in October 2014), now, as far as I know, TLA + is used in 14 projects, not 10. Another example relates to designing the XBox 360. An intern came to Charles Tecker and wrote specification for memory system. Thanks to this specification, a bug was found that otherwise would not have been noticed, and because of which each XBox 360 would fall after four hours of use. IBM engineers confirmed that their tests would not have discovered this bug.

For more information about TLA +, you can read on the Internet, and now let's talk about informal specifications. We rarely have to write programs that compute the smallest common factor and the like. Much more often, we write programs like the pretty print printer tool I wrote for TLA +. After the simplest processing, the TLA + code would look like this:

But in the above example, the user most likely wanted the conjunction and equality signs to be aligned. So correct formatting would look more like this:

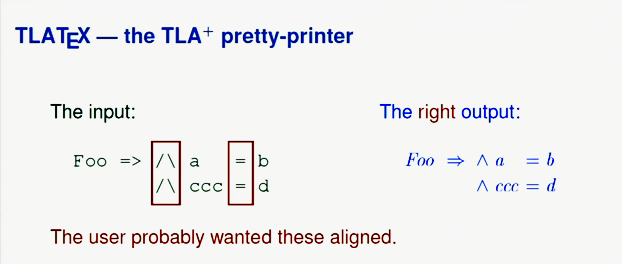
Consider another example:

Here, on the contrary, the alignment of the signs of equality, addition and multiplication in the source was random, therefore the simplest processing itself is quite sufficient. In general, there is no exact mathematical definition of correct formatting, because “correct” in this case means “what the user wants,” and this cannot be mathematically determined.

It would seem that if we do not have a definition of truth, then the specification is useless. But it is not. If we don’t know what the program should do, it doesn’t mean that we don’t need to think about its work - on the contrary, we have to spend even more on it. The specification here is especially important. It is impossible to determine the optimal program for structural printing, but this does not mean that we should not take it at all, and writing code as a stream of consciousness is not the case. As a result, I wrote a specification of six rules with definitions in the form of comments in a Java file. Here is an example of one of the rules: a left-comment token is LeftComment aligned with its covering token . This rule is written in, say, mathematical English: LeftComment aligned , left-comment and covering token are terms with definitions. This is how mathematicians describe mathematics: they write definitions of terms and, based on them, the rules. The benefit of such a specification is that it is much easier to understand and debug six rules than 850 lines of code. I must say that it was not easy to write these rules, it took quite a lot of time to debug them. Especially for this purpose, I wrote code that reported exactly which rule is used. Due to the fact that I checked these six rules with a few examples, I did not need to debug 850 lines of code, and the bugs were quite easy to find. Java has excellent tools for this. If I just wrote the code, then it would take me much more time, and the formatting would be of worse quality.

Why it was impossible to use a formal specification? On the one hand, the correctness of the implementation here is not too important. Structural printout surely will not please someone, so I didn’t have to seek correct work in all non-ordinary situations. More importantly, I did not have the right tools. The TLA + model validator is useless here, so I would have to manually write examples.

This specification has features common to all specifications. It is a higher level than the code. You can implement it in any language. To write it useless any tools or methods. No programming course will help you write this specification. And there are no tools that could make this specification unnecessary, unless, of course, you are not writing a language specifically for writing TLA + structural print programs. Finally, this specification says nothing about how exactly we will write code, it only indicates what this code does. We are writing a specification to help us think through a problem before we start thinking about code.

But this specification has features that distinguish it from other specifications. 95% of other specifications are significantly shorter and simpler:

Further, this specification is a set of rules. This is usually a sign of poor specs. It is rather difficult to understand the consequences of a set of rules, which is why I had to spend a lot of time debugging them. However, in this case I could not find a better way.

It is worth saying a few words about programs that run continuously. As a rule, they work in parallel, for example, operating systems or distributed systems. Very few people can understand them in mind or on paper, and I don’t belong to them, although once I could do it. Therefore, we need tools that will check our work - for example, TLA + or PlusCal.

Why was it necessary to write a specification if I already knew what exactly the code should do? In fact, it only seemed to me as if I knew it. In addition, if there is a specification, the stranger no longer needs to get into the code in order to understand what he is doing. I have a rule: there should be no general rules. This rule, of course, has an exception, this is the only general rule that I follow: the specification of what the code does should tell people everything they need to know when using this code.

So, what exactly do programmers need to know about thinking? For a start, the same as everyone: if you don’t write, it only seems to you that you are thinking. In addition, you need to think before you code, which means you need to write, before you code. The specification is what we write before we start coding. The specification is needed for any code that can be used or modified by anyone. And this “someone” can be the author of the code itself a month after writing it. Specification is needed for large programs and systems, for classes, for methods, and sometimes even for complex sections of a particular method. What exactly needs to be written about the code? It is necessary to describe what it does, that is, something that can be useful to anyone using this code. Sometimes it may also be necessary to specify exactly how the code achieves its goal. If this method we passed in the course of the algorithms, then we call it an algorithm. If it is something more special and new, then we call it high-level design. There is no formal difference: both are abstract models of the program.

How exactly should write the code specification? The main thing: it should be a level above the code itself. It should describe the state and behavior. It must be as strict as the task requires. If you are writing a specification for how to implement a task, you can write it in pseudo-code or using PlusCal. Learning to write specifications is necessary on formal specifications. This will give you the necessary skills that will help including with the informal. How to learn to write formal specifications? When we studied programming, we wrote programs and then debugged them. : , . TLA+, , , . TLA+ , .

? , . , . , .

, . , , . , . . , , . , . , .

— . — Amazon. . ? . , , . , . — , . . .

. - , , . , - , , . . , . , , . , ? -, , , , . , . , . , , . -, , . . , , .

, , . - . , — . , , . , , , , . . , . , , — . , .

TLA+ PlusCal , . , .

, . — , . , Hydra 2019, 11-12 2019 -. .