When is it worth testing the hypothesis of no less effectiveness?

An article from the Stitch Fix team suggests using a non-inferiority trials clinical research approach in marketing and product A / B tests. Such an approach is really applicable when we are testing a new solution that has advantages that are not measured by tests.



The simplest example is the reduction of bones. For example, we automate the process of assigning the first lesson, but do not want to drop the end-to-end conversion much. Or we test changes that are oriented to one user segment, while ensuring that conversions to other segments do not slacken much (when testing several hypotheses, we don’t forget about corrections).



Choosing the right margin of no less efficiency adds additional difficulties at the design stage of the test. The question of how to choose Δ in the article is not very well disclosed. It seems that this choice is not completely transparent in clinical trials. A review of medical publications on non-inferiority reports that only in half of the publications the choice of the border is justified and often these justifications are ambiguous or not detailed.

')

In any case, this approach seems interesting, since by reducing the required sample size can increase the speed of testing, and, therefore, the speed of decision making. - Daria Mukhina, Skyeng Food Analyst.



The Stitch Fix team likes to test different things. The whole technology community likes to conduct tests in principle. Which version of the site attracts more users - A or B? Does version A of the recommender model make more money than version B? Almost always, to test hypotheses, we use the simplest approach from the basic course of statistics:







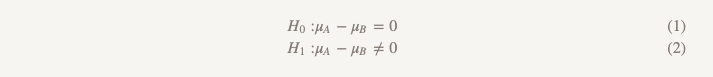
Although we rarely use this term, this form of testing is called “testing the hypothesis of superiority”. With this approach, we assume that there is no difference between the two options. We adhere to this idea and discard it only if the data obtained are convincing enough for this — that is, they demonstrate that one of the options (A or B) is better than the other.



The test of the superiority hypothesis is suitable for solving a variety of problems. We release the B-version of the recommender model only if it is obviously better than the already used version A. But in some cases this approach does not work so well. Consider a few examples.



1) We use a third-party service that helps identify fake bank cards. We found another service that costs significantly less. If a cheaper service works as well as the one we use now, we will choose it. It does not have to be better than the service used.



2) We want to discard data source A and replace it with data source B. We could postpone rejecting A, if B produces very bad results, but continue to use A is not possible.



3) We would like to move from approach to modeling A to approach B, not because we expect better results from B, but because it gives us greater operational flexibility. We have no reason to believe that B will be worse, but we will not make the transition if this is so.



4) We made several qualitative changes to the website design (version B) and we believe that this version is superior to version A. We do not expect changes in conversion or any key performance indicators, which we usually rate the website. But we believe that there are advantages in the parameters that are either immeasurable, or our technologies are not enough to measure.



In all these cases, excellence research is not the most appropriate solution. But most professionals in such situations use it by default. We carefully conduct an experiment to correctly determine the magnitude of the effect. If it were true that versions A and B work in a very similar way, there is a chance that we will not be able to reject the null hypothesis. Do we conclude that A and B generally work the same way? Not! The inability to reject the null hypothesis and the acceptance of the null hypothesis is not the same thing.



Sample size calculations (which you, of course, conducted) are usually carried out with more stringent boundaries for type I errors (probability of erroneous deviation of the null hypothesis, often called alpha) than for type II errors (probability of being unable to reject the null hypothesis, provided the null hypothesis is erroneous, often called beta). The typical value for alpha is 0.05, while the typical value for beta is 0.20, which corresponds to a statistical power of 0.80. This means that since we can not detect the true influence of the magnitude that we indicated in our calculations of power, with a probability of 20% and this is a rather serious information gap. As an example, let's consider such hypotheses:







H0: my backpack is NOT in my room (3)

H1: my backpack in my room (4)



If I searched my room and found my backpack, fine, I can reject the null hypothesis. But if I looked around the room and could not find my backpack (Figure 1), what conclusion should I draw? Am I sure that he is not there? Did I search carefully enough? What if I searched only 80% of the room? To conclude that the backpack is definitely not in the room will be a rash decision. Not surprisingly, we cannot "accept the null hypothesis."



The area we searched

We did not find a backpack - should we accept the null hypothesis?



Figure 1. Searching 80% of a room is about the same as conducting a study with a power of 80%. If you did not find a backpack, having examined 80% of the room, is it possible to conclude that it is not there?



So what should a data expert do in this situation? You can greatly increase the power of research, but then you will need a much larger sample, and the result will still be unsatisfactory.



Fortunately, such problems have long been studied in the world of clinical research. Drug B is cheaper than drug A; drug B is expected to cause fewer side effects than drug A; drug B is easier to transport because it does not need to be stored in the refrigerator, but drug A is necessary. Check the hypothesis of no less efficiency. This is necessary to show that version B is as good as version A - at least within a certain predetermined limit of “no lesser efficiency,” Δ. A little later we will talk more about how to set this limit. But now suppose that this is the minimum difference that is practically significant (in the context of clinical trials this is usually called clinical significance).



Hypotheses about not less efficiency turn everything upside down:







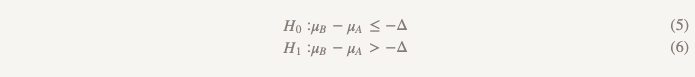
Now, instead of assuming that there is no difference, we assume that version B is worse than version A, and we will stick to this assumption until we demonstrate that this is not the case. This is exactly the moment when it makes sense to use testing one-sided hypothesis! In practice, this can be done by building a confidence interval and determining whether the interval is indeed larger than Δ (Figure 2).

Choice Δ

How to choose Δ? The Δ selection process includes a statistical rationale and subject assessment. In the world of clinical research, there are regulatory recommendations, from which it follows that the delta should be the smallest clinically significant difference - one that will be important in practice. Here is a quotation from the European leadership, with which you can check yourself: “If the difference was chosen correctly, the confidence interval, which lies entirely between –∆ and 0 ..., is still sufficient to demonstrate no less efficiency. If this result does not seem acceptable, it means that ∆ was not chosen properly. ”



Delta definitely should not exceed the magnitude of the effect of version A with respect to the true control (placebo / no treatment), as this leads us to the fact that version B is worse than true control, and at the same time demonstrates "no less effective." Suppose that when version A was introduced, version 0 was in its place or the function did not exist at all (see Figure 3).



According to the results of testing the superiority hypothesis, the magnitude of the effect E was revealed (that is, presumably μ ^ A − μ ^ 0 = E). Now A is our new standard, and we want to make sure that B is not inferior to A. Another way to write down μB − μA≤ − Δ (null hypothesis) is μB≤μA − Δ. If we assume what to do is equal to or greater than E, then μB ≤ μA – E ≤ placebo. Now we see that our estimate for μB completely exceeds μA − E, which thereby completely refutes the null hypothesis and allows us to conclude that B is not inferior to A, but at the same time μB can be ≤ μ placebo, and this is not what do we need. (Figure 3).





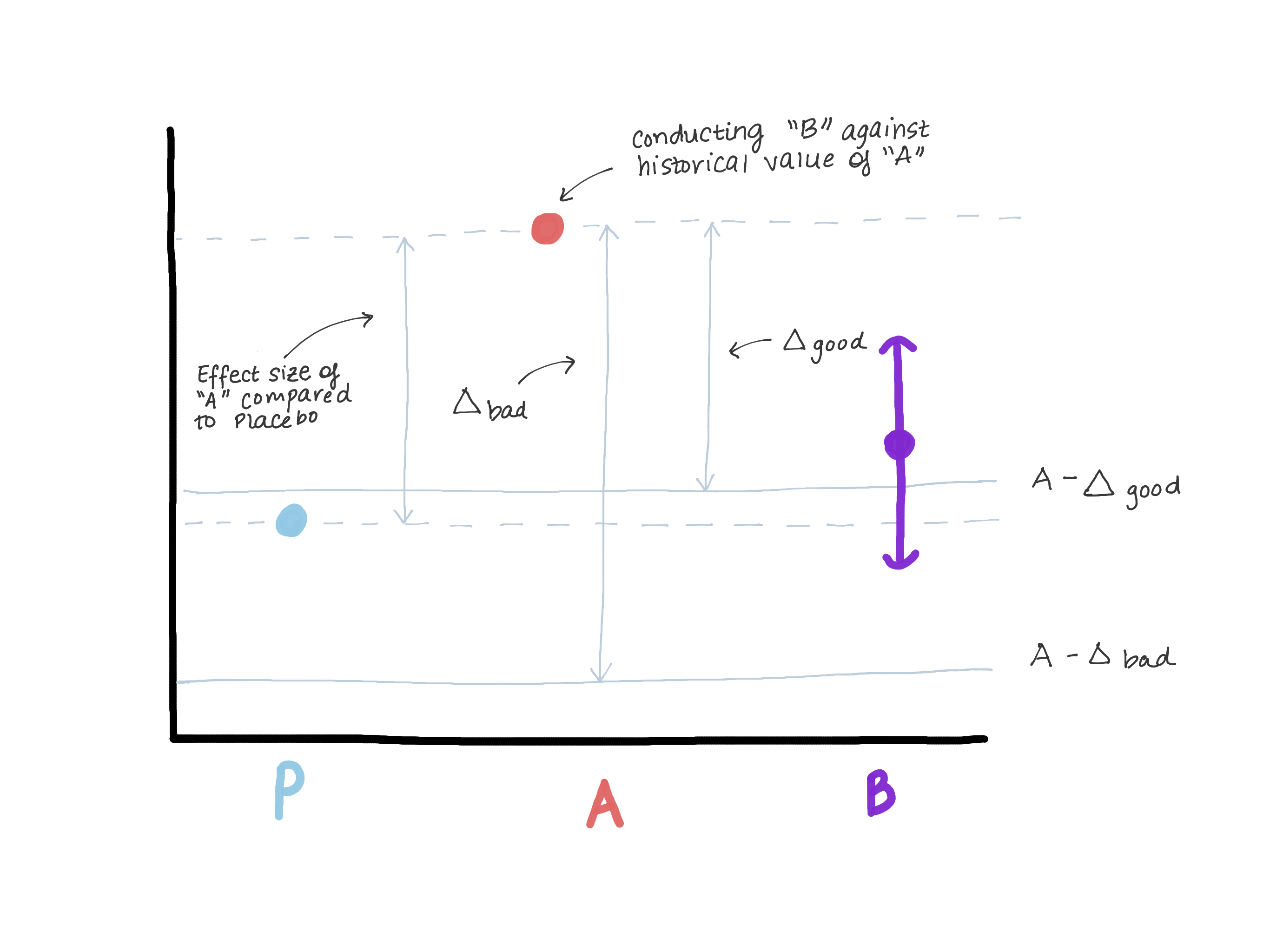
Figure 3. Demonstration of the risks of choosing a border of no lesser efficiency If the limit is too large, it can be concluded that B is not inferior to A, but at the same time indistinguishable from placebo. We will not change the drug, which is clearly more effective than placebo (A), to a drug that has the same efficacy as placebo.

Choice α

We proceed to the choice of α. You can use the standard value α = 0.05, but this is not entirely fair. Like, for example, when you buy something on the Internet and use several discount codes at once, although they should not be added up - just the developer made a mistake, and you got away with it. According to the rules, the value of α should be equal to half the value of α, which is used when testing the hypothesis of superiority, that is, 0.05 / 2 = 0.025.

Sample size

How to estimate sample size? If you think that the true difference between the means between A and B is 0, then the calculation of the sample size will be the same as in the test of the superiority hypothesis, except that you replace the size of the effect with a limit of no less efficiency, provided that use α no less efficiency = 1 / 2α superiority (αnon-inferiority = 1 / 2αsuperiority). If you have reason to believe that option B may be a little worse than option A, but you want to prove that it is worse by no more than Δ, then you are lucky! In fact, this reduces the size of your sample, because it is easier to demonstrate that B is worse than A, if you actually believe that it is a little worse, and not equivalent.

Solution example

Suppose you want to switch to version B, provided that it is worse than version A by no more than 0.1 points on a 5-point customer satisfaction scale ... Let's approach this problem using the superiority hypothesis.



To test the superiority hypothesis, we would calculate the sample size as follows:







That is, if you have 2103 observations in your group, you can be 90% sure that you will find an effect of 0.10 or more. But if the value of 0.10 is too great for you, you may not need to test the superiority hypothesis for it. Perhaps for reliability you decide to conduct research for a smaller effect size, for example, 0.05. In this case, you need 8407 observations, that is, the sample will increase by almost 4 times. But what if we stick to our initial sample size, but increase the power to 0.99 so that we do not doubt if we get a positive result? In this case, n for one group will be 3676, which is better, but increases the sample size by more than 50%. And as a result, we still simply can not refute the null hypothesis, and do not get an answer to your question.



What if, instead, we test a hypothesis of no less effectiveness?







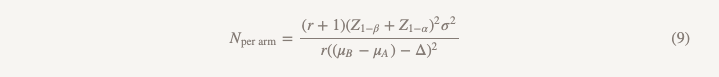
The sample size will be calculated using the same formula, with the exception of the denominator.

Differences from the formula used in testing the hypothesis of superiority are as follows:



- Z1 − α / 2 is replaced by Z1 − α, but if you do everything according to the rules, you replace α = 0.05 with α = 0.025, that is, they are the same number (1.96)



- appears in the denominator (μB − μA)



- θ (magnitude of the effect) is replaced by Δ (the limit is not lower efficiency)



If we assume that µB = µA, then (µB - µA) = 0 and calculating the sample size for a limit of no smaller efficiency is exactly what we would get when calculating the superiority for an effect size of 0.1, great! We can conduct a study of the same scale with different hypotheses and a different approach to the conclusions, and we will get an answer to a question we really want to answer.



Now suppose that we really do not assume that µB = µA and

we think that µB is slightly worse, maybe by 0.01 units. This increases our denominator, reducing the sample size per group to 1737.



What happens if version B is actually better than version A? We refute the null hypothesis that B is worse than A, more than Δ and accept the alternative hypothesis that B, if worse, is not worse than Δ, and can be better. Try to put this conclusion in a cross-functional presentation and see what happens (seriously, try it). In a situation where you need to focus on the future, no one wants to settle for “worse by no more than Δ and, possibly, better.”



In this case, we can conduct a study that is very briefly called “testing the hypothesis that one of the options is superior to the other or inferior to it”. It uses two sets of hypotheses:



The first set (the same as when testing the hypothesis of no less efficiency):







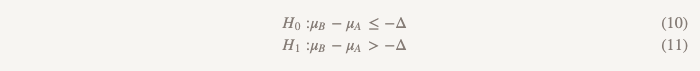
The second set (the same as when testing the hypothesis of superiority):







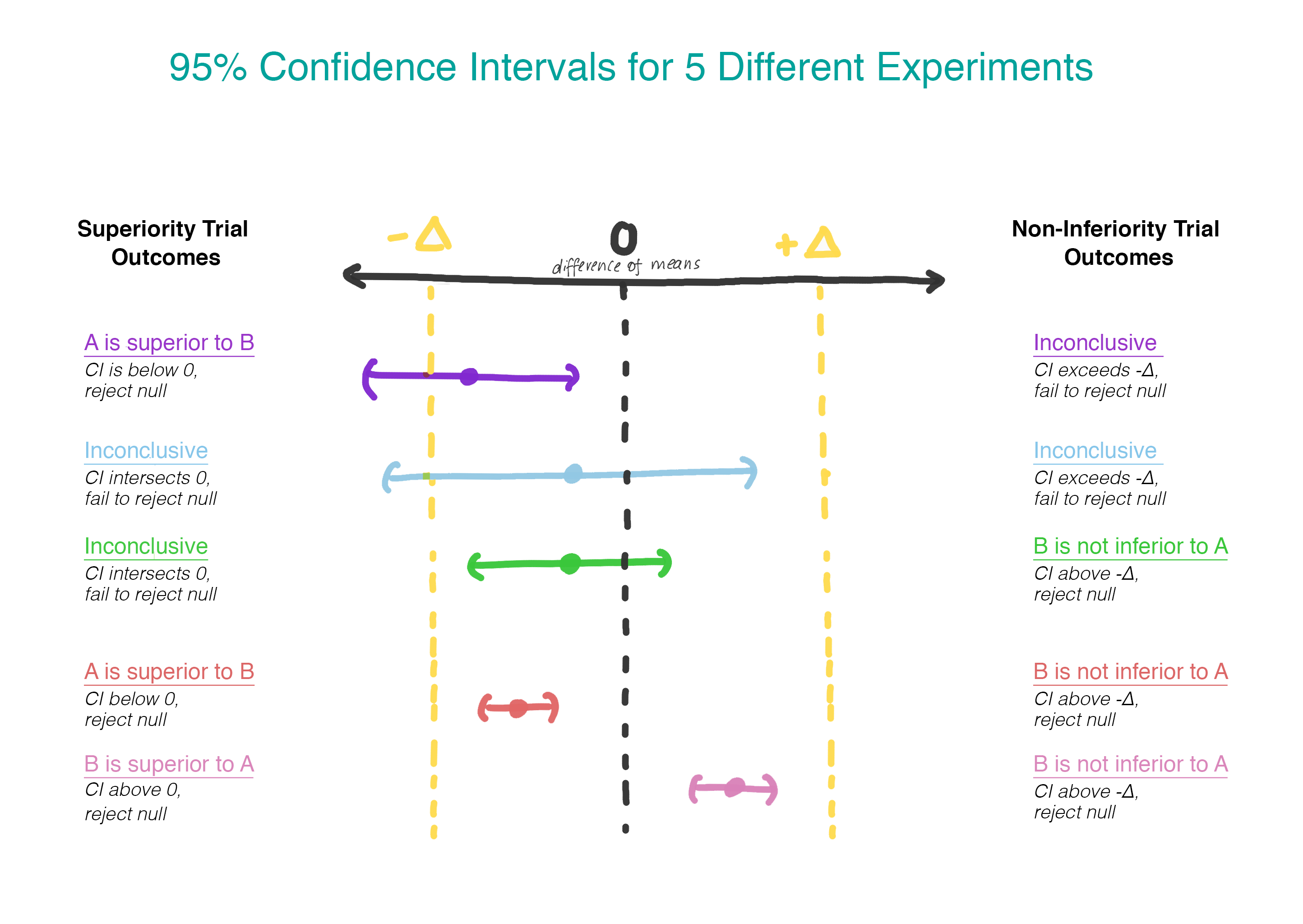
We test the second hypothesis only if the first one is rejected. With sequential testing, we maintain the overall level of errors of the first kind (α). In practice, this can be achieved by creating a 95% confidence interval for the difference between averages and checking to determine if the entire interval is Δ. If the interval does not exceed -Δ, we cannot reject the zero value and stop. If the entire interval really exceeds −Δ, we will continue and see if the interval contains 0.



There is another type of research that we have not discussed - equivalence studies.



Studies of this type may be replaced by studies to test the hypothesis of no less effectiveness and vice versa, but in fact they have an important difference. The test to test the hypothesis of no less effectiveness aims to show that option B is at least as good as A. And the equivalence study aims to show that option B is at least as good as A, and option A is as good as B, which is more difficult. In essence, we are trying to determine whether the entire confidence interval for the difference in averages between −Δ and Δ. Such studies require a larger sample size and are less frequent. Therefore, the next time when you will conduct a study in which your main task is to make sure that the new version is not worse, do not settle for “the inability to refute the null hypothesis”. If you want to test a really important hypothesis, consider the various options.