Geekly Articles each Day
📜 ⬆️ ⬇️

Solving Japanese crosswords with P̶y̶t̶h̶o̶̶n̶ Rust and WebAssembly

Rust logo as nonogram


How to make a solver (solver) of nonograms in Python, rewrite it in Rust to run directly in a browser via WebAssembly.


TL; DR


Start


About Japanese crosswords (nonograms) on Habré there were already several posts. Example
and one more .


Images are encrypted with numbers to the left of the rows, as well as above the columns. The number of numbers shows how many groups of black (or their own color, for color crossword puzzles) cells are in the corresponding row or column, and the numbers themselves - how many flat cells each of these groups contains (for example, a set of three numbers - 4, 1, and 3 means that there are three groups in this series: the first is from four, the second is from one, the third is from three black cells). In a black-and-white crossword, groups should be separated by at least one empty cell, in color this rule applies only to monochrome groups, and multi-colored groups can be located closely (empty cells can be along the edges of the rows). It is necessary to determine the placement of groups of cells.

One of the most common points of view is that only correct ones can be called “correct” crossword puzzles. Usually, this is how a solution method is called, in which the dependencies between different rows and / or columns are not taken into account. In other words, a solution is a sequence of independent decisions of individual rows or columns, until all cells are painted over (for more details about the algorithm, see below). For example, only such nonograms can be found at http://nonograms.org/ ( http://nonograms.ru/ ). Nonograms from this site have already been cited as an example in the article Solving colored Japanese crosswords with the speed of light . For comparison and verification purposes, support for downloading and parsing crosswords from this site has also been added to my solver (thanks to KyberPrizrak for permission to use materials from his site).


However, it is possible to extend the concept of nonograms to a more general problem, when the usual “logical” method leads to a dead end. In such cases, to solve, you have to make an assumption about the color of a cell and then, having proved that this color leads to a contradiction, mark the opposite color for this cell. The sequence of such steps can (if there is enough patience) give us all the solutions. About solving such a more general case of crossword puzzles and will be mainly this article.


Python


About a year and a half ago, I accidentally stumbled upon an article in which I was told how to solve one line (as it turned out later, the method was rather slow).


When I implemented this method in Python (my main working language) and added a sequential update of all lines, I saw that all of this was not solved very quickly. After studying the materiel, it turned out that there are a lot of works and implementations on this topic that offer different approaches for this task.


It seemed to me that the most extensive work on the analysis of various implementations of solvers was done by Jan Wolter, publishing on his website (which, as far as I know, remains the largest public repository of nonograms on the Internet) a detailed study containing a huge amount of information and links that can help creating your solver.


Studying numerous sources (will be at the end of the article), I gradually improved the speed and functionality of my solver. As a result, I was dragged out and I was engaged in the implementation, refactoring, debugging algorithms for about 10 months in the working time.


Basic algorithms


The resulting solver can be represented in the form of four levels of solution:





So, we begin to solve our crossword puzzle from the second level (the first one is suitable only for a degenerate case, when there is only one row or column in the whole crossword puzzle) and gradually move up the levels. As you might guess, each level several times causes the underlying level, so for an effective solution it is extremely necessary to have fast first and second levels, which can be called millions of times for complex puzzles.


At this stage it turns out (quite expectedly) that python is not at all the tool that is suitable for maximum performance in such a CPU-intensive task: all the calculations in it are extremely inefficient compared to lower-level languages. For example, the most algorithmically close BGU-solver (in Java) was 7–17 (sometimes up to 27) times faster on a variety of tasks.


Read more
         pynogram_my BGU_my speedup
 Dancer 0.976 0.141 6.921986      
 Cat 1.064 0.110 9.672727      
 Skid 1.084 0.101 10.732673     
 Bucks 1.116 0.118 9.457627      
 Edge 1.208 0.094 12.851064     
 Smoke 1.464 0.120 12.200000     
 Knot 1.332 0.140 9.514286      
 Swing 1.784 0.138 12.927536     
 Mum 2.108 0.147 14.340136     
 DiCap 2.076 0.176 11.795455     
 Tragic 2.368 0.265 8.935849      
 Merka 2.084 0.196 10.632653     
 Petro 2.948 0.219 13.461187     
 M & M 3.588 0.375 9.568000      
 Signed 4.068 0.242 16.809917     
 Light 3.848 0.488 7.885246      
 Forever 111.000 13.570 8.179808  
 Center 5.700 0.327 17.431193     
 Hot 3.150 0.278 11.330935     
 Karate 2.500 0.219 11.415525     
 9-Dom 510.000 70.416 7.242672      
 Flag 149.000 5.628 26.474769     
 Lion 71.000 2.895 24.525043     
 Marley 12.108 4.405 2.748695      
 Thing 321,000 46.166 6.953169      
 Nature inf 433.138 inf     
 Sierp inf inf NaN      
 Gettys inf inf NaN

The measurements were taken on my machine, the puzzles are taken from the standard set, which Jan Wolter used in his comparison


And this is already after I started using PyPy, and on standard CPython the calculation time was 4-5 times higher than on PyPy! We can say that the performance of a similar Java solver turned out to be higher than CPython code by 28-85 times.


Attempts to improve the performance of my solver with the help of profiling (cProfile, SnakeViz, line_profiler) led to some acceleration, but they certainly didn’t give a supernatural result.


Results :


+ Solver can solve all puzzles from https://webpbn.com , http://nonograms.org and its own (ini-based) format


+ solves black-and-white and color nonograms with any number of colors (the maximum number of colors that was encountered is 10)


+ Solves puzzles with missing block sizes (blotted). An example of such a puzzle .


+ can render puzzles to the console / to the curses window / to the browser (when installing the additional option pynogram-web ). For all modes, viewing the progress of the solution in real time is supported.


- slow calculations (in comparison with the implementations described in the article-comparison of solvers, see table ).


- ineffective backtracking: some puzzles can be solved for hours (when the decision tree is very large).


Rusty


Earlier this year, I began to study Rust. I started, as usual, with The Book , I learned about WASM, I went through the proposed tutorial . However, I wanted some real task in which the strengths of the language could be acted upon (first of all, its super-performance), and not examples invented by someone. So I went back to the nonograms. But now I already had a working version of all the algorithms in Python, it remains “only” to rewrite.


From the very beginning, the good news was waiting for me: it turned out that Rust, with its type system, perfectly describes the data structures for my task. For example, one of the basic matches BinaryColor + BinaryBlock / MultiColor + ColoredBlock allows you to permanently separate black and white and colored nonograms. If somewhere in the code we try to solve a color string using ordinary binary description blocks, we get a compilation error about the type mismatch.


Base types look like this.
 pub trait Color { fn blank() -> Self; fn is_solved(&self) -> bool; fn solution_rate(&self) -> f64; fn is_updated_with(&self, new: &Self) -> Result<bool, String>; fn variants(&self) -> Vec<Self>; fn as_color_id(&self) -> Option<ColorId>; fn from_color_ids(ids: &[ColorId]) -> Self; } pub trait Block { type Color: Color; fn from_str_and_color(s: &str, color: Option<ColorId>) -> Self { let size = s.parse::<usize>().expect("Non-integer block size given"); Self::from_size_and_color(size, color) } fn from_size_and_color(size: usize, color: Option<ColorId>) -> Self; fn size(&self) -> usize; fn color(&self) -> Self::Color; } #[derive(Debug, PartialEq, Eq, Hash, Clone)] pub struct Description<T: Block> where T: Block, { pub vec: Vec<T>, } // for black-and-white puzzles #[derive(Debug, PartialEq, Eq, Hash, Copy, Clone, PartialOrd)] pub enum BinaryColor { Undefined, White, Black, BlackOrWhite, } impl Color for BinaryColor { // omitted } #[derive(Debug, PartialEq, Eq, Hash, Default, Clone)] pub struct BinaryBlock(pub usize); impl Block for BinaryBlock { type Color = BinaryColor; // omitted } // for multicolor puzzles #[derive(Debug, PartialEq, Eq, Hash, Default, Copy, Clone, PartialOrd, Ord)] pub struct MultiColor(pub ColorId); impl Color for MultiColor { // omitted } #[derive(Debug, PartialEq, Eq, Hash, Default, Clone)] pub struct ColoredBlock { size: usize, color: ColorId, } impl Block for ColoredBlock { type Color = MultiColor; // omitted }

When migrating the code, some moments clearly indicated that a statically typed language, such as Rust (or, for example, C ++), is more suitable for this task. More precisely, generics and traits describe the subject area better than class hierarchies. So in the Python code, I had two classes for a linear BguSolver , BguSolver and BguColoredSolver which decided, respectively, the black-and-white line and the color line. In the Rust code, I still have a single generic structure struct DynamicSolver<B: Block, S = <B as Block>::Color> , which can solve both types of tasks, depending on the type transferred during creation ( DynamicSolver<BinaryBlock>, DynamicSolver<ColoredBlock> ). This, of course, does not mean that something similar cannot be done in Python, just in Rust the type system explicitly indicated to me that if you do not go this way, you will have to write a ton of duplicate code.


In addition, anyone who tried to write on Rust undoubtedly noticed the effect of "trusting" the compiler, when the process of writing code reduces to the following pseudo-meta-algorithm:


 write_initial_code
 while (compiler_hints = $ (cargo check))! = 0;  do
     fix_errors (compiler_hints)
 end

When the compiler stops issuing errors and warnings, your code will be coordinated with the type system and borrow checker and you will warn in advance of a heap of potential bugs (of course, subject to careful design of data types).


I will give a couple of examples of functions that show how concise Rust code can be (compared to Python analogues).


unsolved_neighbours

List the unresolved "neighbors" for a given point (x, y)


 def unsolved_neighbours(self, position): for pos in self.neighbours(position): if not self.is_cell_solved(*pos): yield pos 

 fn unsolved_neighbours(&self, point: &Point) -> impl Iterator<Item = Point> + '_ { self.neighbours(&point) .into_iter() .filter(move |n| !self.cell(n).is_solved()) }

partial_sums

For a set of blocks describing a single line, give partial amounts (taking into account the mandatory intervals between blocks). The resulting indices will indicate the minimum position where the block can end (this information is used further for a linear solver).


For example, for such a set of blocks [2, 3, 1] we have the output [2, 6, 8] , which means that the first block can be shifted to the left as much as possible so that its right edge occupies the 2nd cell, similarly for the rest blocks:


             1 2 3 4 5 6 7 8 9 
             _ _ _ _ _ _ _ _ _
      2 3 1 | _ | _ | _ | _ | _ | _ | _ | _ | _ | 
               ^ ^ ^
               |  |  |
 end of block 1 |  |  | 
 end of block 2 -------- |
 end of block 3 ------------


 @expand_generator def partial_sums(blocks): if not blocks: return sum_so_far = blocks[0] yield sum_so_far for block in blocks[1:]: sum_so_far += block + 1 yield sum_so_far 

 fn partial_sums(desc: &[Self]) -> Vec<usize> { desc.iter() .scan(None, |prev, block| { let current = if let Some(ref prev_size) = prev { prev_size + block.0 + 1 } else { block.0 }; *prev = Some(current); *prev }) .collect() }

When porting, I made a few changes.



Useful tools



Performance


That for the sake of what was being started and rewriting Rust. We take crosswords from the already mentioned comparison table and run them through the best solvers described in the original article. Results and description of the runs here . We take the resulting file and build a couple of graphs on it. Since the solution time varies from milliseconds to tens of minutes, the graph is executed with a logarithmic scale.


run on a jupyter laptop
 import pandas as pd import numpy as np import matplotlib.pyplot as plt %matplotlib inline # strip the spaces df = pd.read_csv('perf.csv', skipinitialspace=True) df.columns = df.columns.str.strip() df['name'] = df['name'].str.strip() # convert to numeric df = df.replace('\+\ *', np.inf, regex=True) ALL_SOLVERS = list(df.columns[3:]) df.loc[:,ALL_SOLVERS] = df.loc[:,ALL_SOLVERS].apply(pd.to_numeric) # it cannot be a total zero df = df.replace(0, 0.001) #df.set_index('name', inplace=True) SURVEY_SOLVERS = [s for s in ALL_SOLVERS if not s.endswith('_my')] MY_MACHINE_SOLVERS = [s for s in ALL_SOLVERS if s.endswith('_my') and s[:-3] in SURVEY_SOLVERS] MY_SOLVERS = [s for s in ALL_SOLVERS if s.endswith('_my') and s[:-3] not in SURVEY_SOLVERS] bar_width = 0.17 df_compare = df.replace(np.inf, 10000, regex=True) plt.rcParams.update({'font.size': 20}) def compare(first, others): bars = [first] + list(others) index = np.arange(len(df)) fig, ax = plt.subplots(figsize=(30,10)) df_compare.sort_values(first, inplace=True) for i, column in enumerate(bars): ax.bar(index + bar_width*i, df_compare[column], bar_width, label=column[:-3]) ax.set_xlabel("puzzles") ax.set_ylabel("Time, s (log)") ax.set_title("Compare '{}' with others (lower is better)".format(first[:-3])) ax.set_xticks(index + bar_width / 2) ax.set_xticklabels("#" + df_compare['ID'].astype(str) + ": " + df_compare['name'].astype(str)) ax.legend() plt.yscale('log') plt.xticks(rotation=90) plt.show() fig.savefig(first[:-3] + '.png', bbox_inches='tight') for my in MY_SOLVERS: compare(my, MY_MACHINE_SOLVERS) compare(MY_SOLVERS[0], MY_SOLVERS[1:])

python solver

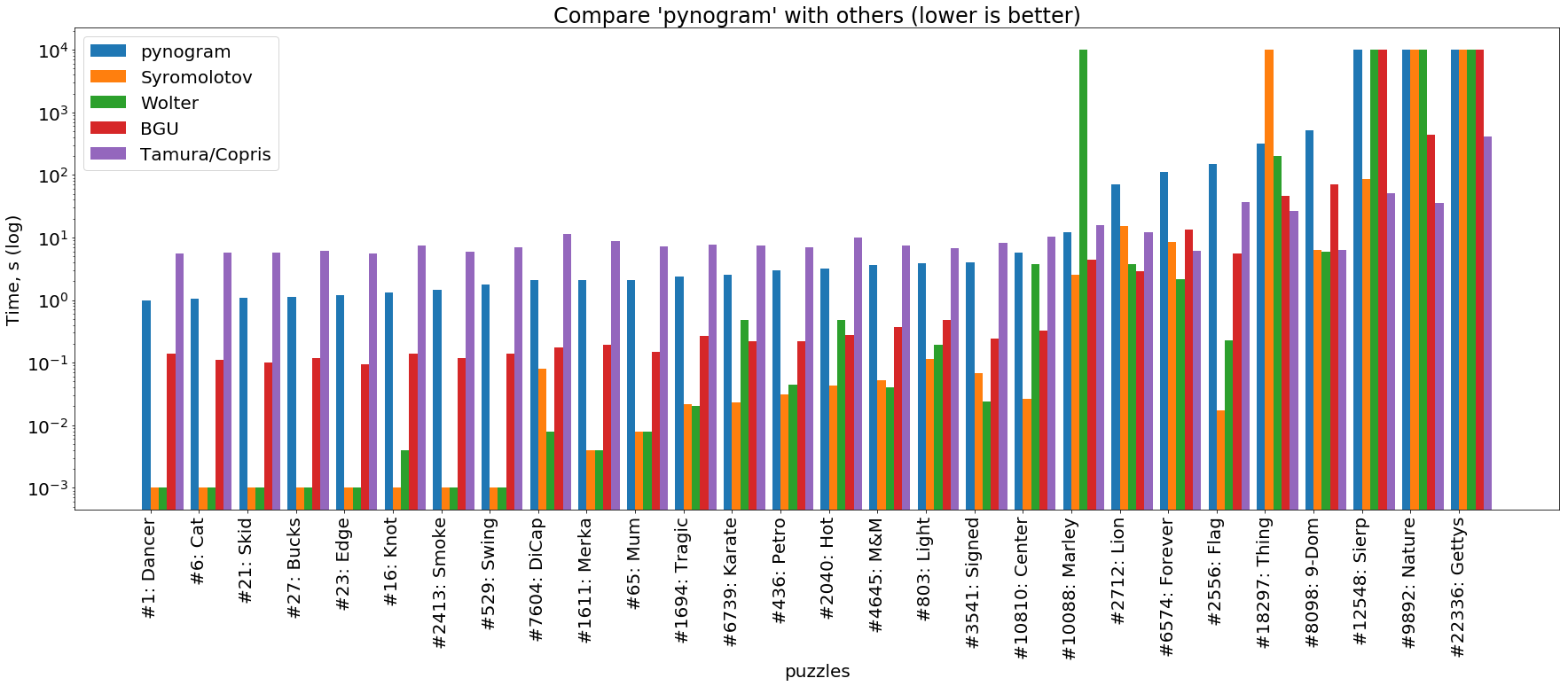
pynogram-performance

(the picture is clickable )


We see that the pynogram here is the slowest of all represented solvers. The only exception to this rule is the Tamura / Copris solver, based on the SAT, which solves the simplest puzzles (the left part of the graph) longer than ours. However, such is the peculiarity of SAT-solvers: they are designed for super complex crosswords, in which an ordinary solver is stuck in backtracking for a long time. This is clearly visible on the right side of the chart, where Tamura / Copris solves the most difficult puzzles tens and hundreds of times faster than any other.


rustler

nonogrid-performance

(the picture is clickable )


This graph shows that nonogrid copes with simple tasks as well or slightly worse than high-performance solvers written in C and C ++ ( Wolter and Syromolotov ). With the complication of tasks, our solver roughly repeats the trajectory of a BGU solver (Java), but almost always advances it by an order of magnitude. On the most difficult tasks, Tamura / Copris is always ahead of everyone.


rust vs python

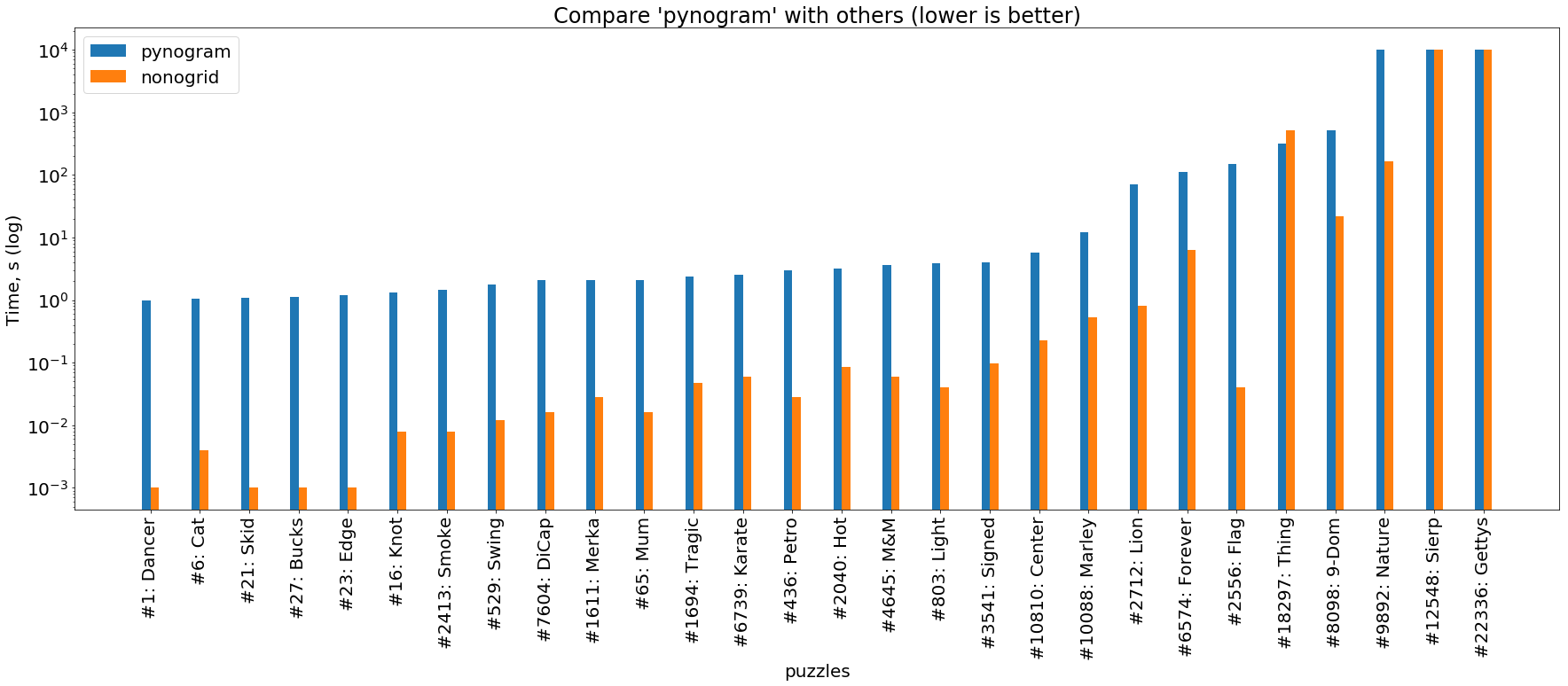
py-vs-rust-performance

(the picture is clickable )


Well, finally, a comparison of our two solvers, described here. It can be seen that the Rust-solver is almost always ahead of the Piton solver by 1–3 orders of magnitude.


Results :


+ Solver can solve all puzzles from https://webpbn.com (except blotted - with partially hidden block sizes), http://nonograms.org and its own (TOML-based) format


+ solves black and white and color nonograms with any number of colors


+ can render puzzles to console (color c with webpbn.com draws truly color)


+ works quickly (in comparison with the implementations described in the article-comparison of solvers, see table).


- backtracking remained inefficient, as in the Python-solution: some puzzles (for example , such a harmless 20x20 ) can be solved for hours (when the decision tree is very large). Perhaps instead of backtracking, you should use the SAT-solvers already mentioned in the habr . True, the only SAT-solver I found on Rust at first glance seems to be underdeveloped and abandoned.


WebAssembly


So, rewriting the code to Rust has borne fruit: the solver has become much faster. However, Rust offers us another incredibly cool feature: compiling to WebAssembly and the ability to run your code directly in the browser.


To implement this feature, there is a special tool for Rust, which provides the necessary binders and generates a boilerplate for you to run Rust functions painlessly in the JS code - this wasm-pack (+ wasm-bindgen ). Most of the work with it and other important tools is already described in the Rust and WebAssembly tutorial . However, there are a couple of things that I had to figure out on my own:



WASM- JS, WASM . - ( ), HashMap , . ( JS) , / .


, Mutex , thread-safe. smart- . thread-safe Rc Arc RefCell RwLock . : 30%. --features=threaded thread-safe , WASM-.


6574 8098 ( 10 ):


idnon-thread-safethread-safeweb-interface
65745.47.49.2
809821.528.429.9

, - 40..70% , , (32..37%) thread-safe ( cargo build --release --features=threaded ).


Firefox 67.0 Chromium 74.0.


WASM- ( ). https://webpbn.com/ http://www.nonograms.org/


Todo



Results




  1. The 'pbnsolve' Paint-by-Number Puzzle Solver by Jan Wolter and the survey
  2. The BGU Nonograms Project
  3. Solving Nonograms by combining relaxations
  4. An Efficient Approach to Solving Nonograms
  6. Color and black and white Japanese crosswords on-line
  8. 'Nonolib' library by Dr. Steven Simpson
  9. Rust and WebAssembly

')

Source: https://habr.com/ru/post/454586/

More articles:


All Articles