ARA: algorithm for finding the maximum number of points on a straight line
Recently, I came across a classic task for interviews: finding the maximum number of points on a straight line (on a plane, the coordinates are integers). The idea of complete enumeration immediately came to mind, which has an obvious time complexity in O (n ^ 2), but it seemed to me that there must be something else here, at least some alternative in O (n * log (n)) . After half an hour there was even something better!
A more detailed formulation of the problem with input-output examples is on GeeksForGeeks and LeetCode
At first I noticed that you can easily solve the problem only for horizontal or vertical lines, adding the X / Y of each point into a dictionary. What is the difference between the other lines? Just a slope? .. But this is fixable!
')
So I decided that it was possible to bypass the entire list of points several times by rotating them. And the solution is obtained in O (n)! Although with a large ratio. I really hope that I did not invent the bike :)
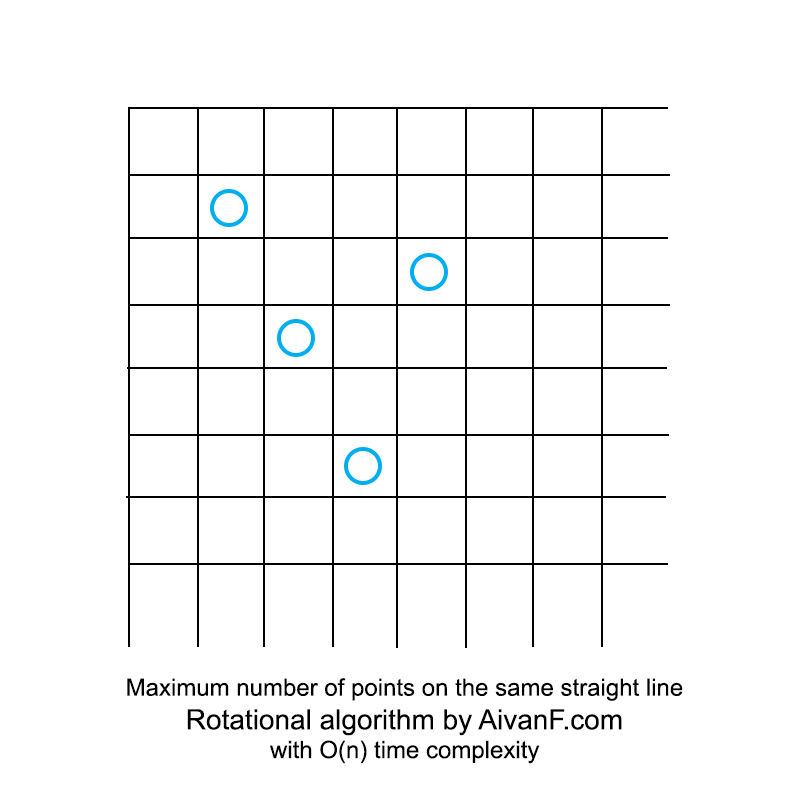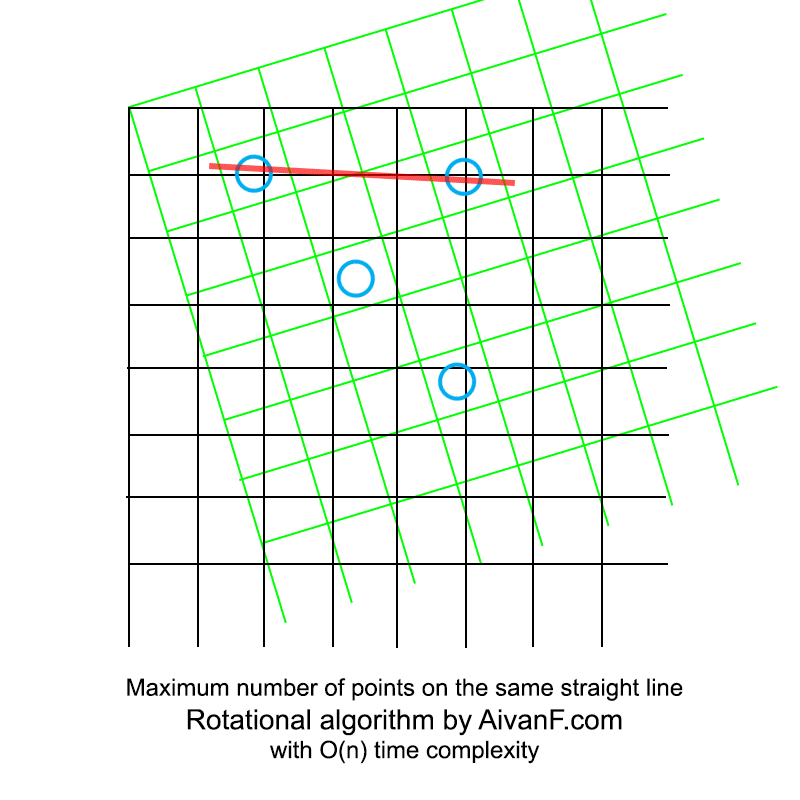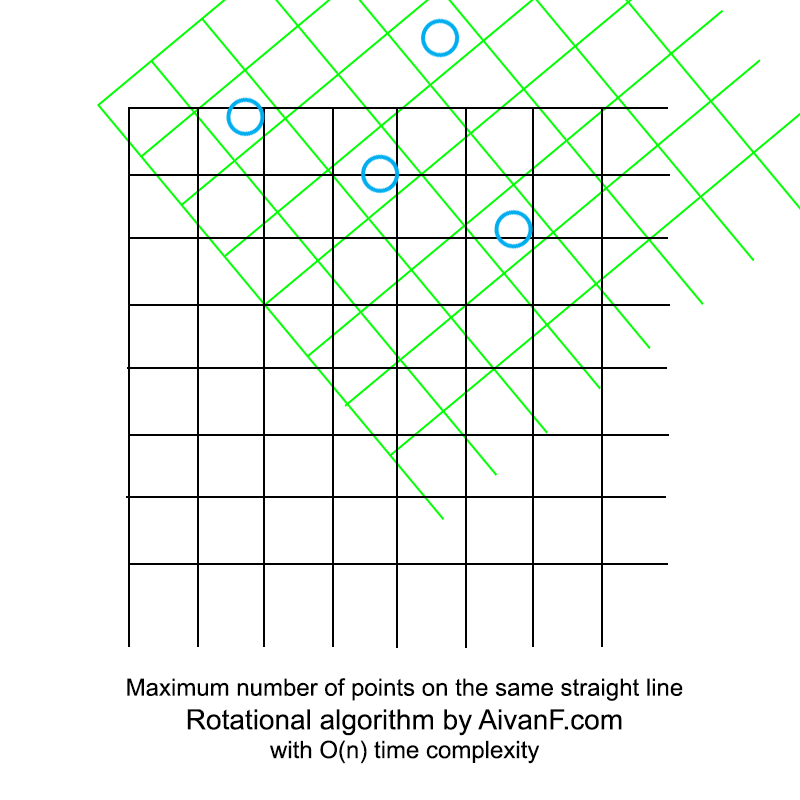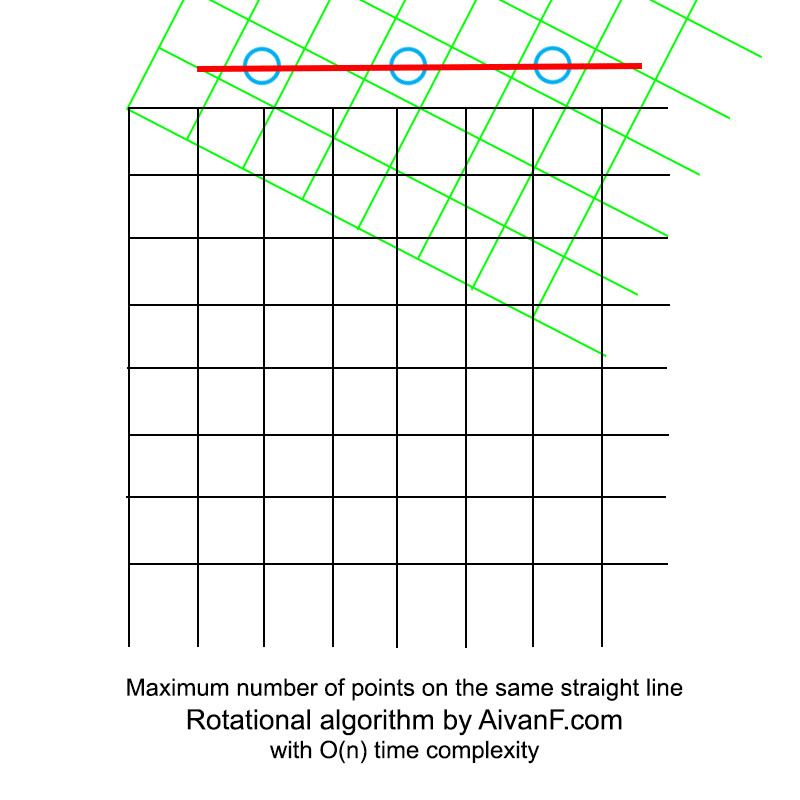
Visualized it looks like this:
My first homemade gif, please do not scold :)
It is interesting to note that the subsequent implementation of complete brute force took more lines of code.
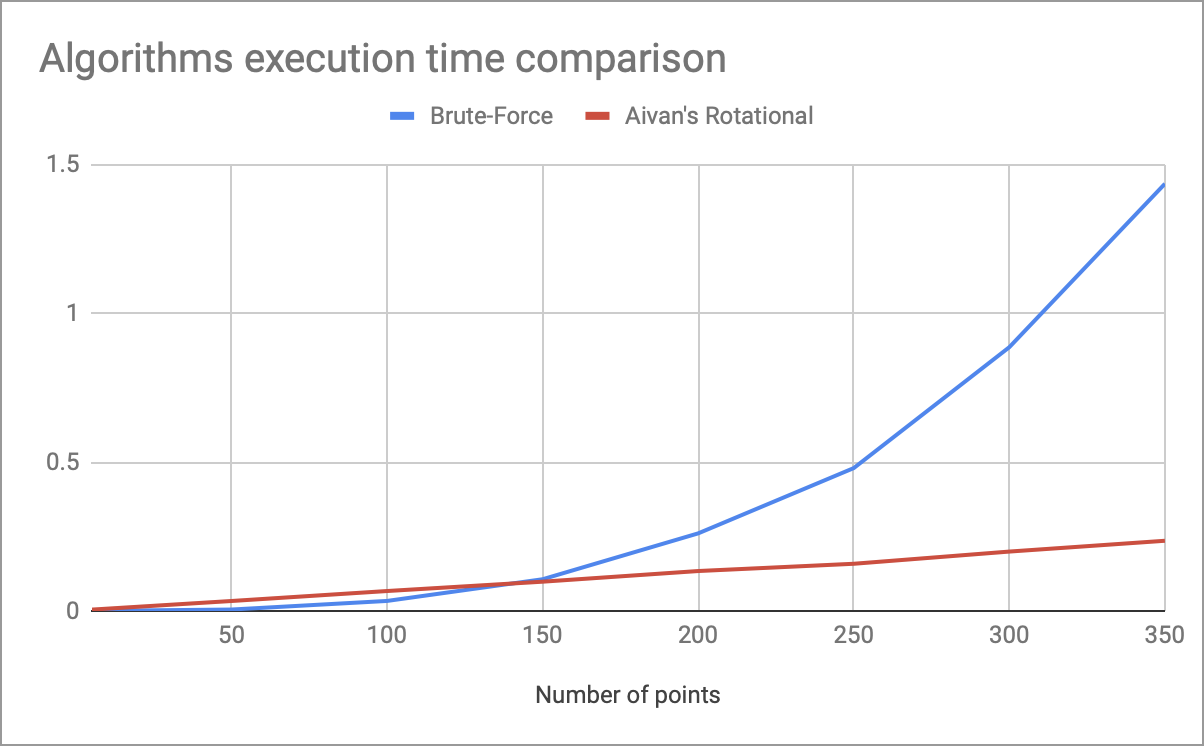
The graph with measurements of the execution time of my rotational algorithm and complete enumeration, depending on the number of points, is in the header.
Approximately 150 points show the advantage of linear complexity in time (with coefficients used in the code above). As a result, this algorithm has such disadvantages:
And such advantages:
A table with measurements is available here . The entire project source code with both algorithms and various checks is on GitHub .
Update. I want to note once again that this algorithm has both advantages and disadvantages, I do not advocate it as an ideal replacement for brute force, I just described an interesting possible alternative, which in some cases may be more appropriate.

A more detailed formulation of the problem with input-output examples is on GeeksForGeeks and LeetCode
At first I noticed that you can easily solve the problem only for horizontal or vertical lines, adding the X / Y of each point into a dictionary. What is the difference between the other lines? Just a slope? .. But this is fixable!
')
So I decided that it was possible to bypass the entire list of points several times by rotating them. And the solution is obtained in O (n)! Although with a large ratio. I really hope that I did not invent the bike :)
# *** *** # # = 180/ROT_COUNT # # 12, # 180*4 (6% ), # 180*20 (0% ). # ó . # - . ROT_COUNT = 180*10 # # , # 1 / MULT_COEF. # 4 . # MULT_COEF ROT_COUNT. # ó - . # - . MULT_COEF = 2 ** 3 angles = list(map(lambda x: x*180.0/ROT_COUNT, range(ROT_COUNT))) def mnp_rotated(points, angle): """Returns Maximum Number of Points on the same line with given rotation""" # rad = math.radians(angle) co = math.cos(rad) si = math.sin(rad) # counts = {} for pair in points: # nx = pair[0]*co - pair[1]*si # , # # # nx = int(nx * MULT_COEF) # if nx in counts: counts[nx] += 1 else: counts[nx] = 1 # return max(counts.values()) def mnp(points): """Returns Maximum Number of Points on the same line""" res = 0 best_angle = 0 # for i in angles: current = mnp_rotated(points, i) # , if current > res: res = current best_angle = i return res Visualized it looks like this:
My first homemade gif, please do not scold :)

It is interesting to note that the subsequent implementation of complete brute force took more lines of code.
The graph with measurements of the execution time of my rotational algorithm and complete enumeration, depending on the number of points, is in the header.
Open schedule here

Approximately 150 points show the advantage of linear complexity in time (with coefficients used in the code above). As a result, this algorithm has such disadvantages:
- The accuracy of the work is not absolute.
- Runtime on small sets of points is large.
In general, this is easily corrected by correct selection of coefficients: for simple sets, ROT_COUNT = 36 is enough, not 2000, which speeds up the code 50+ times.
And such advantages:
- Works calmly with fractional coordinates.
- The time complexity is linear, which is noticeable on large data sets.
A table with measurements is available here . The entire project source code with both algorithms and various checks is on GitHub .
Update. I want to note once again that this algorithm has both advantages and disadvantages, I do not advocate it as an ideal replacement for brute force, I just described an interesting possible alternative, which in some cases may be more appropriate.
Source: https://habr.com/ru/post/454388/
All Articles