An unexpected look at asynchronous circuits, independent of speed
In asynchronous science, the central place is occupied by the property of circuits, called independence from speed, in English speed independent (hereinafter referred to as SI). It is believed that this property is analogous to the independence of asynchronous circuits from the delays of logical elements. Not surprisingly, the term SI is mentioned in almost every work on asynchrony. But from time to time some vague doubts arise on the part of this term. It is no coincidence that this term is increasingly being replaced by another term called self-timing. Referring to the original source will help clarify this situation. This is the second volume of R. Miller's Theory of Switching Circuits, and more specifically, Chapter 10, called The Theory of Switching Circuits independent of Speed.
So, here is the definition of speed independent schemes.

')
A (equivalence) class is a complete set of admissible states of a circuit such that for any state from this set there exists a sequence of admissible states beginning with a given state and containing all the states of a given set. In other words, from any state of a class, you can get into any state of the same class.
A class (equivalence) is final if it is not possible to move from a state of a given class to a state belonging to another class.
For example, all living patterns (behaviors) are speed independent. They also do not depend on the speed of the circuit, which eventually stops, and in a single state.
Further, the author establishes a connection between SI schemes on the one hand, and semimodular, sequential, distributive schemes on the other hand. And in conclusion he gives a list of remarkable properties of circuits that are not dependent on speed.

The first point is especially interesting. It says that speed-independent circuits do not depend on the delay of logic elements. Unfortunately, the text does not explicitly provide the basis for this conclusion. Perhaps this is the reason for the subsequent misunderstandings about the term SI. In fact, this conclusion is completely fair. At the beginning of Chapter 10, the author presents the rules for calculating subsequent states.

The transition of the circuit to the next state is a consequence of switching the output of some logical element (or outputs of several elements). That is, the time interval between the creation of conditions for switching a logical element (excitation) and the switching itself is not limited by anything. And such a period of time is the delay of the logical element. That is, from the very beginning, the author proceeds from the assumption that the delays of logical elements can be arbitrarily large. Indeed, the following is written a little further.

Well, to dispel all doubts, quote from the first page of chapter 10.

Thus, an indisputable fact is established: independence from the delays of logical elements is not a property of the circuit, but a property of the model in which this circuit is investigated. That is, any scheme, SI or non-SI, studied in the same way as R. Miller describes, is independent of the delays of the logic elements. At the same time, any scheme can be investigated in a model with limited delay. In such a model, the set of admissible states is a subset of the set of admissible states when considering the same scheme in a model with an unlimited delay of elements. When studying a circuit in a model with a limited delay of elements, the scheme can be independent of speed and at the same time depend on element delays.
Thus, it turns out that the independence of the circuit from the delays of logical elements is in no way connected with the SI property. Then the question arises: what is the point of introducing the definition of independence from speed? Indeed, consider the two schemes and their behavior.
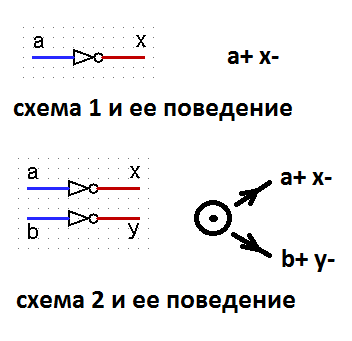
Signals a, b for both schemes are input, signals x, y are output. Both schemes implement perfectly reasonable behaviors. But at the same time, scheme 1 does not depend on speed, and scheme 2 does not possess such a property. Yes, we can say that the definition of SI is introduced without dividing the signals into input and output. But such a separation of signals by the author was implied, and there is a remark in the text about this.
The meaningfulness and reasonableness of introducing the definition of the property SI is revealed only in connection with the property of semimodularity. For circuits with the semimodularity property, each signal can relieve its excitation only through its own switching. Non-semimodular circuits in the physical implementation of glitches and metastable states. Only semimodular circuits can be considered stable.
But the connection between the properties of semi-modularity and independence from speed is one-sided. That is, semi-modular circuits do not depend on speed, but the reverse is not true. SI schemes may not be semi-modular. That is a really important property dividing the schemes on the basis of stability, it is semi-modularity. It is important to understand that semimodular circuits can also depend on the delays of logic elements, if we consider them in a model with limited delay.
But that's not all. The semimodularity property is also defined for autonomous circuits, that is, without separating the signals into input and output. Because of this, free-choice schemes (behaviors) do not meet the criteria for semimodularity. Meanwhile, these schemes can be as stable as semi-modular ones. For example, the above scheme 2 is not semi-modular, but in terms of stability it is not inferior to scheme 1, which is semi-modular.
There is a way out of this impasse. In the book J. Cortadella, M. Kishinevsky, A. Kondratyev, L. Lavagno, A. Yakovlev "Logic Synthesis for Asynchronous Controllers and Interfaces", the definition of the output persistency (OP) property is given.

It is the OP property that is the actual property that separates patterns (behaviors) into stable and non-stable. It is the OP property that should take the place of the SI property. In this case, one should not forget that independence from the delays of logical elements is a property of the model in which the schemes (behavior) are studied. And OP circuits may also be dependent on element delays if considered in a model with limited delay.
Despite all the previous criticism, there are no complaints about R. Miller. There are no logical errors in his work. The blame for more than half a century of delusion lies more likely on the readers who incorrectly interpreted the work of R. Miller.
Well, finally a pleasant conclusion from the foregoing. The STG behavior description model has unlimited logical element delay. The rules for changing the marking, extracting the truth table are formulated from the assumption of unlimited delay of elements. Consequently, any scheme obtained by calculating logical functions by STG (either using the truth table, or directly on the graph), is certainly independent of the delays of the logical elements. However, it should be understood that further manipulations with the resulting scheme can lead to the loss of this valuable quality.
So, here is the definition of speed independent schemes.

')
A (equivalence) class is a complete set of admissible states of a circuit such that for any state from this set there exists a sequence of admissible states beginning with a given state and containing all the states of a given set. In other words, from any state of a class, you can get into any state of the same class.
A class (equivalence) is final if it is not possible to move from a state of a given class to a state belonging to another class.
For example, all living patterns (behaviors) are speed independent. They also do not depend on the speed of the circuit, which eventually stops, and in a single state.
Further, the author establishes a connection between SI schemes on the one hand, and semimodular, sequential, distributive schemes on the other hand. And in conclusion he gives a list of remarkable properties of circuits that are not dependent on speed.

The first point is especially interesting. It says that speed-independent circuits do not depend on the delay of logic elements. Unfortunately, the text does not explicitly provide the basis for this conclusion. Perhaps this is the reason for the subsequent misunderstandings about the term SI. In fact, this conclusion is completely fair. At the beginning of Chapter 10, the author presents the rules for calculating subsequent states.

The transition of the circuit to the next state is a consequence of switching the output of some logical element (or outputs of several elements). That is, the time interval between the creation of conditions for switching a logical element (excitation) and the switching itself is not limited by anything. And such a period of time is the delay of the logical element. That is, from the very beginning, the author proceeds from the assumption that the delays of logical elements can be arbitrarily large. Indeed, the following is written a little further.

Well, to dispel all doubts, quote from the first page of chapter 10.

Thus, an indisputable fact is established: independence from the delays of logical elements is not a property of the circuit, but a property of the model in which this circuit is investigated. That is, any scheme, SI or non-SI, studied in the same way as R. Miller describes, is independent of the delays of the logic elements. At the same time, any scheme can be investigated in a model with limited delay. In such a model, the set of admissible states is a subset of the set of admissible states when considering the same scheme in a model with an unlimited delay of elements. When studying a circuit in a model with a limited delay of elements, the scheme can be independent of speed and at the same time depend on element delays.
Thus, it turns out that the independence of the circuit from the delays of logical elements is in no way connected with the SI property. Then the question arises: what is the point of introducing the definition of independence from speed? Indeed, consider the two schemes and their behavior.

Signals a, b for both schemes are input, signals x, y are output. Both schemes implement perfectly reasonable behaviors. But at the same time, scheme 1 does not depend on speed, and scheme 2 does not possess such a property. Yes, we can say that the definition of SI is introduced without dividing the signals into input and output. But such a separation of signals by the author was implied, and there is a remark in the text about this.
The meaningfulness and reasonableness of introducing the definition of the property SI is revealed only in connection with the property of semimodularity. For circuits with the semimodularity property, each signal can relieve its excitation only through its own switching. Non-semimodular circuits in the physical implementation of glitches and metastable states. Only semimodular circuits can be considered stable.
But the connection between the properties of semi-modularity and independence from speed is one-sided. That is, semi-modular circuits do not depend on speed, but the reverse is not true. SI schemes may not be semi-modular. That is a really important property dividing the schemes on the basis of stability, it is semi-modularity. It is important to understand that semimodular circuits can also depend on the delays of logic elements, if we consider them in a model with limited delay.
But that's not all. The semimodularity property is also defined for autonomous circuits, that is, without separating the signals into input and output. Because of this, free-choice schemes (behaviors) do not meet the criteria for semimodularity. Meanwhile, these schemes can be as stable as semi-modular ones. For example, the above scheme 2 is not semi-modular, but in terms of stability it is not inferior to scheme 1, which is semi-modular.
There is a way out of this impasse. In the book J. Cortadella, M. Kishinevsky, A. Kondratyev, L. Lavagno, A. Yakovlev "Logic Synthesis for Asynchronous Controllers and Interfaces", the definition of the output persistency (OP) property is given.

It is the OP property that is the actual property that separates patterns (behaviors) into stable and non-stable. It is the OP property that should take the place of the SI property. In this case, one should not forget that independence from the delays of logical elements is a property of the model in which the schemes (behavior) are studied. And OP circuits may also be dependent on element delays if considered in a model with limited delay.
Despite all the previous criticism, there are no complaints about R. Miller. There are no logical errors in his work. The blame for more than half a century of delusion lies more likely on the readers who incorrectly interpreted the work of R. Miller.
Well, finally a pleasant conclusion from the foregoing. The STG behavior description model has unlimited logical element delay. The rules for changing the marking, extracting the truth table are formulated from the assumption of unlimited delay of elements. Consequently, any scheme obtained by calculating logical functions by STG (either using the truth table, or directly on the graph), is certainly independent of the delays of the logical elements. However, it should be understood that further manipulations with the resulting scheme can lead to the loss of this valuable quality.
Source: https://habr.com/ru/post/454060/
All Articles