How to solve “Minesweeper” (and make it better)

Minesweeper is a simple game with simple rules, but some of its configurations create interesting difficulties. In this article we will create a Minesweeper solver with increasing complexity, and reflect on how the game dynamics change with a gradual increase in the level of assistance. At the end we will develop a new version of the game with a much more interesting gameplay.

Local reasoning: zero neighboring mines

In the original game , one automatic mechanism is used: when a player opens a cage, next to which there are no mines, the game engine opens all the adjacent cells. This does not threaten the game, so you can safely allow the computer to do it, and the situation itself is immediately clear to the player and does not interfere with the gameplay.

Such reasoning is completely local: for deciding on the next action, information of only one cell is taken into account.
')
It is difficult to think of a situation in which the game would become worse without this automatic help. Try to play this game to get an idea of ​​how it goes without automatic opening of cells [in the original article, all the examples are interactive] :

Local considerations taking into account the environment

It will be easy for a new player to understand that if the number of adjacent mines, that is, the number shown in the cell, is equal to the number of undiscovered neighboring cells, then all these cells must be mines, so check the boxes on them. Similarly, when the number of adjacent mines is equal to the number of neighboring flags, the remaining unopened adjacent cells must be empty.

These rules take into account one cell, as well as the state of neighboring (open / checked).

Implementing these rules manually can be fun. If you add a timer, the player begins to learn how to apply them quickly and accurately. This turns the Minesweeper into a reaction game . What happens if we automate these rules?


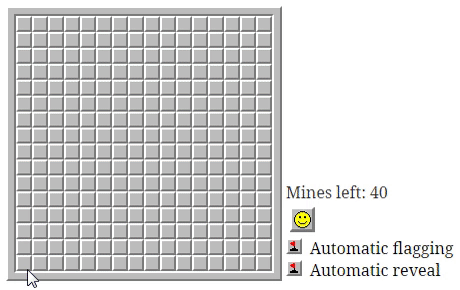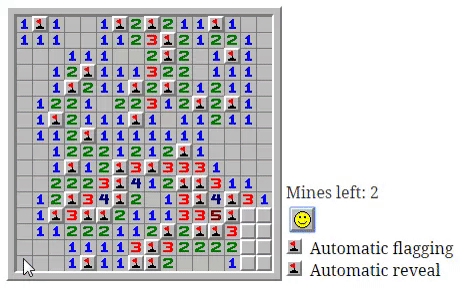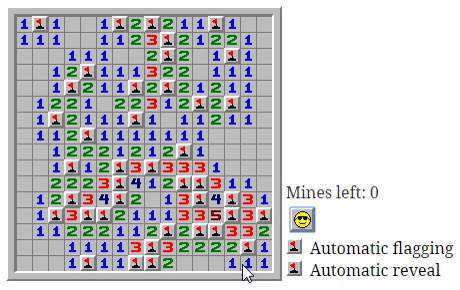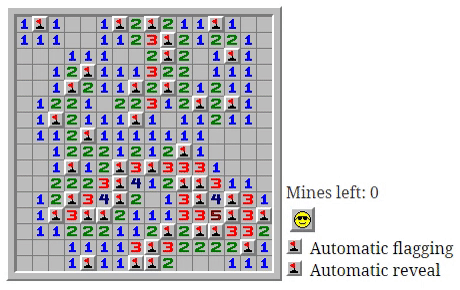
This automation has an interesting side effect - checking the box can have fatal consequences instantly.

Otherwise, we may have situations that can be divided into three categories:

1. Games fully resolved using automatic rules
2. Difficult situations requiring more cells for reasoning
3. The state of the game, in which there is no logical way forward - the player can only choose randomly, possibly taking into account the probabilities.

Situation 1 seems beautiful, but not particularly interesting if it occurs too often. Will such games be better without an automatic solution? Maybe not; such games are very simple even when manually solving, and the player is not particularly interested in playing games that are not difficult. Although, of course, there is always difficulty in the reaction game: you need to act as quickly as possible.

Situation 2 seems to me very attractive. We focus more on solving logical conditions, spending less time on accurate aiming and pressing the right buttons. This makes Minesweeper look more like an active puzzle .

Situation 3 completely destroys all the fun. However, I heard that some people like to play games with randomness .

Is it possible to get rid of situation 3?

Complete solution: global reasoning

For algorithmic detection of all logical conditions necessary for a game state, we need to perform an exhaustive search for all game states. It has been proven that Minesweeper is an NP-complete task . Below is a small, but interesting and illustrative example of the state of the game, which has only one logical solution, but to find it you must take into account the state of the game entirely:


Is it possible to search the entire space of the game states? How many variants of s exist?

Given:

w = field width

h = field height

k = number of minutes

n = w · h

Then the number of possible states s is equal to

$$

$$s = \ begin {pmatrix} n \\ k \ end {pmatrix}$$

For the standard levels "Novice", "Amateur" and "Professional" it gives us:

$$

$$s_b = \ begin {pmatrix} 8 * 8 \\ 10 \ end {pmatrix} = 151473214816$$

$$

$$s_i = \ begin {pmatrix} 16 * 16 \\ 40 \ end {pmatrix} = 1.050 * 10 ^ {47}$$

$$

$$s_e = \ begin {pmatrix} 30 * 16 \\ 99 \ end {pmatrix} = 5.602 * 10 ^ {104}$$

We understand that the naive approach is completely inappropriate here. Let's see how a naive algorithm could look like and find out if it can be optimized for something that works.

Naive algorithm

The task of the algorithm is to find all the logical conditions necessary for a given field state. It would be difficult to implement this by carefully thinking through the decisions; the computer is much better able to cope with a quick pile of stupid actions.

What we can do is “stupid”: generate all possible permutations of the mines for all the remaining mines. If such a permutation corresponds to all open numbers, then it will be the right decision of the game. Then we study all possible permutations, find all possible solutions, but still do not know which of them is correct.

If in all possible solutions there is something in common, either among open cells, or among cells marked as mines, then we understand that this common must be part of the right solution for the current field. And in fact: it is impossible to create the right solution that does not have such matching elements, otherwise we would have discovered them.

Thus, we can find all the logical conditions necessary for the current state of the field.

Cells with and without restrictions

The above algorithm has an obvious problem: the number of states that it needs to investigate. But not all cells are the same. Undiscovered cells next to a number are obviously limited to this number. We call these cells bounded. The remaining cells we call unlimited.

If we implement the above algorithm, but we search only in the state space of bounded cells, and we go back as soon as we break the limit, then in many games we will be able to solve all the logical conditions in a reasonable amount of time:


In the case of unlimited cells, we can’t find out where the mines are located, and we immediately know about it logically. This means that you can exclude them from the calculation and consider only the location of the min near the open numbers.

However, we know that a certain number of mines can fall into many unlimited cells; if there are 6 minutes and 4 restricted cells, then there may be a maximum of 4 mines in the restricted cells, that is, at least 2 minutes must be in unlimited cells. By the same logic, we can sometimes determine that all unlimited cells must be empty or all contain mines.

In the case shown below, we know the positions of all the mines, so the AI ​​must be able to understand that the remaining cells are not occupied:


In the following case, we do not know the positions of all the mines, but we can understand that the remaining mine needs to be placed in one of the two cells in the upper left. This means that the cell remaining in the lower right corner is free:

Version with randomness

If we automatically launch the global solver, we will get the optimized version of the “Saper”:


You can divide the games in this version into three categories:

1. Games in which the player makes a random selection and wins.
2. Games in which the player makes a random selection and loses.
3. Games in which the work of AI requires a lot of time, and the player can actually use reasoning.

Obviously, this is a game with accidents. What is the appeal of such games? From the point of view of logic, the game shown above is similar to this:


But which of the random games is better? It seems that the meaning of other games with randomness lies in the existence of a complex connection between player's actions and victory / loss. For drawing lottery numbers, complex machines are used, which are not specifically in a hurry to choose a number and make the whole show out of showing this number.

Perhaps a large field that is solved automatically is a pretty good game.
with accidents, given that the player is watching the gradual opening of all cells.

Can we think of a different type of game?

Deterministic version

Now we have an AI capable of determining all the logical steps from a given state of the game. Sometimes he will not be able to find logical steps. In such situations, the player has to guess and he can lose if he is not lucky.

What if we add another rule? When the game has no logical way forward, we can ask for help. If the AI ​​agrees that the player cannot do anything, then he comes to the rescue. Otherwise, the player loses immediately. This can be interesting. What kind of help would that be? Perhaps you need to open one cell, regardless of the presence of mines in it:


Thus, we completely got rid of situations in which it was possible to lose by chance.

However, there is one exception: there is still the possibility of degenerate situations in which the global solver cannot complete the computation within a reasonable period of time. Unfortunately, this is the inevitable result of the fact that the “Minesweeper” task is NP-complete.

How does the button “Ask for help” affect the gameplay? She leads the game to focus more on logic; This is the most "puzzling" version of "Minesweeper". Someone might think that the game will be easier, but in fact it becomes more complicated. Now the player’s mistakes have no excuses, and the button will punish him if he misses something. Without a button, it is easy to come to the conclusion that you have exhausted all the logical possibilities and the only scenario is to try to guess randomly. But because of the existence of the button, the player must be right in this assessment.

Finally

Having implemented the full Minesweeper solver, we were able to create a kind of game that was free from its curse: now it’s impossible to lose because you have to choose randomly when you’ve almost decided the whole field. This version differs from the original game only in those moments when you need to guess at random, so I can assume that it is much more exciting than the original game.

In addition, we developed a version of the game that automatically resolves simple local rules. Whether or not to use such help is up to you. It shifts the focus of the game from a mechanical click to a more puzzling gameplay. At the same time it is not necessary to use the improvement of the gameplay, which is provided by the button “Ask for help”.