On the study of non-stationary processes
It is well known that most of the time series that a researcher has to deal with are non-stationary, and their analysis is noticeably more complicated than the study of stationary processes. Since interest in wavelets seems to have subsided, it is useful to discuss some other "non-stationary" tools, suitable primarily for estimating instantaneous frequencies, as well as for estimating instantaneous spectra.
First of all, it makes sense to recall the "analytical signal". Below, the “An-model” is referred to as just finding the instantaneous impedance and power of the test signal after it has been completed with an imaginary part (shifted in phase by π / 2).
But it is not always possible to tinker with the Gilbert transform. Earlier it was already mentioned about the autoregressive spectral estimation method, suitable for working with short sequences. Under the “AR-model”, here we will mean the study of short (out of 5 samples) overlapping fragments of the original signal in order to determine the autoregression coefficients of the 2nd order, finding the “poles” of the model, etc.
')

Both methods described here are based on the same principle — the assumption that in a certain small neighborhood of a selected point in time the process under study can be approximated by an “exponential” sequence — one complex (An) or the sum of two complex conjugate exponentials (AR).
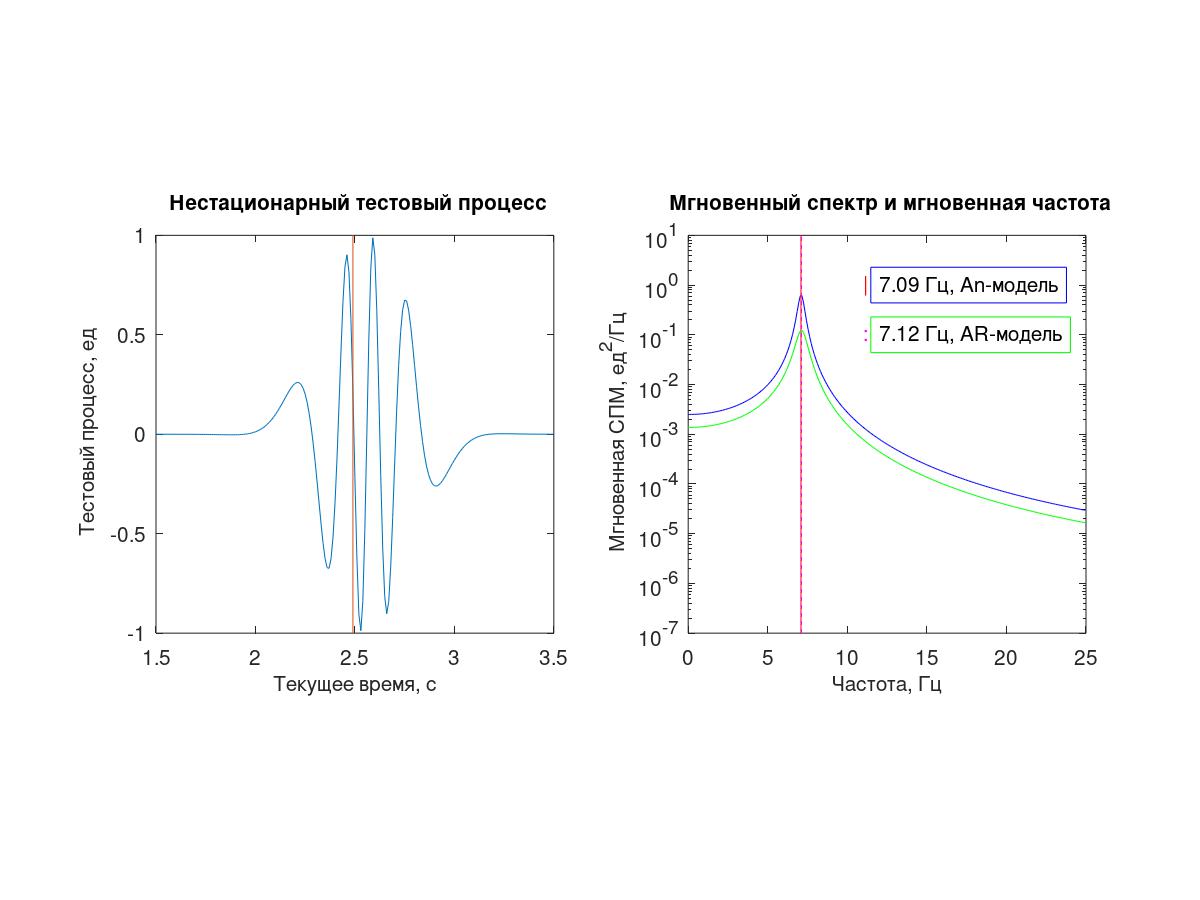
As a test process, a sequence of 512 samples with a conditional sampling interval Δt = 0.01 s, obtained from a continuous deterministic process (1), was used.
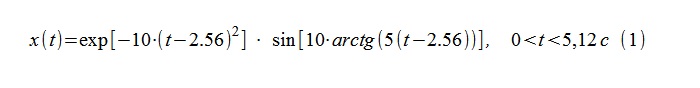
"Logarithmic" and the subsequent differentiation, respectively, of high-frequency filling and the envelope from (1), obtained theoretical expressions for (instantaneous) frequency and decrement (2)

For the An-modeling by the periodogram method (direct and inverse Fourier transform), the analytical signal y [i] is generated from the initial sequence x [i].
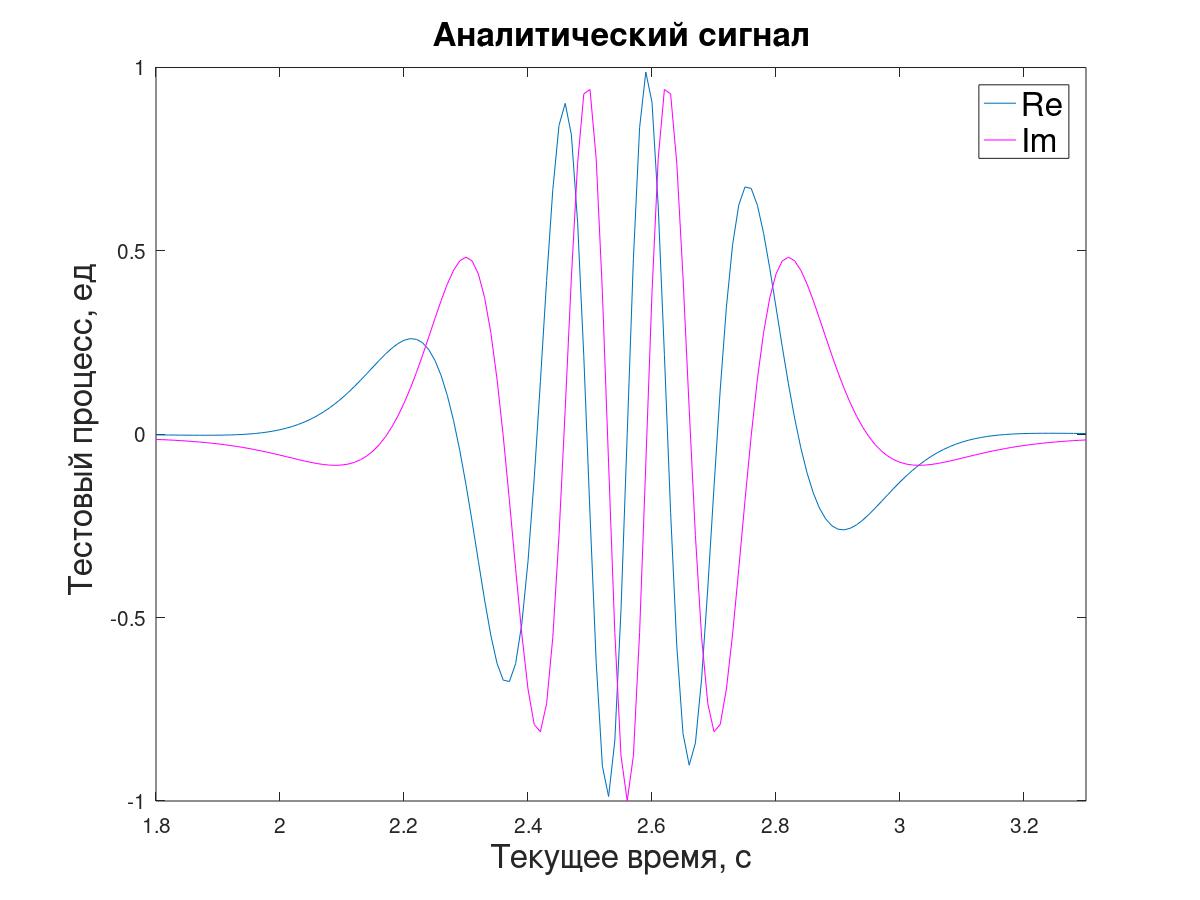
The ratio of two consecutive samples of such a signal, in principle, allows us to determine the instantaneous impedance λ, but to simplify this demonstration task - not to bother with creating intermediate samples or explaining the shift of the estimate by Δt / 2 - it was decided to work with samples “through one”, calculating λ i with respect to the subsequent y [i + 1] signal value to the previous y [i-1] (3).

For AR-modeling (second-order model), the standard procedure for calculating the autocorrelation coefficients 1, a 1i , a 2i was applied using the Yule-Walker equations, while the 5-sample sequences x [i-2], x [i -1], ... x [i + 2] (4).
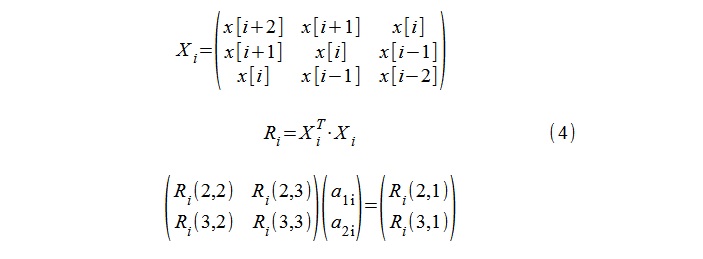
The “poles” of the λ i model are then easily calculated by the logarithm of the roots of the quadratic equation (5).
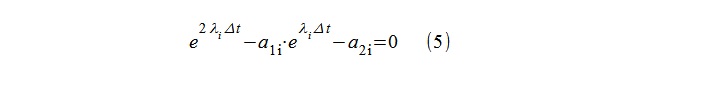

The construction of spectral estimates for the known "poles" up to a scale factor is not difficult . Further. “Instantaneous power” for the An-model is defined in an obvious way, as | y [i] | 2 , and the issue of scaling this estimate appears to have been exhausted. For the AR model, the usual technique associated with determining the power of the conventional white noise in the case of a non-stationary signal “does not work”. In the absence of the best ideas, scaling was applied, based on the average square of the corresponding 5 counts. It seems that nothing more can be done by analyzing only the 5-sample sequence. In the animation, one can see how the ARM graph of the SPM sometimes “perceptibly” fails relative to the An-score. It should be understood that the moments of the “zero crossing” for an AR-model can present difficulties not only in terms of errors with an instantaneous frequency, but also with an instantaneous amplitude, especially in the low-frequency region.
A few comments at the end.
First of all, it makes sense to recall the "analytical signal". Below, the “An-model” is referred to as just finding the instantaneous impedance and power of the test signal after it has been completed with an imaginary part (shifted in phase by π / 2).
But it is not always possible to tinker with the Gilbert transform. Earlier it was already mentioned about the autoregressive spectral estimation method, suitable for working with short sequences. Under the “AR-model”, here we will mean the study of short (out of 5 samples) overlapping fragments of the original signal in order to determine the autoregression coefficients of the 2nd order, finding the “poles” of the model, etc.
')


Both methods described here are based on the same principle — the assumption that in a certain small neighborhood of a selected point in time the process under study can be approximated by an “exponential” sequence — one complex (An) or the sum of two complex conjugate exponentials (AR).
As a test process, a sequence of 512 samples with a conditional sampling interval Δt = 0.01 s, obtained from a continuous deterministic process (1), was used.
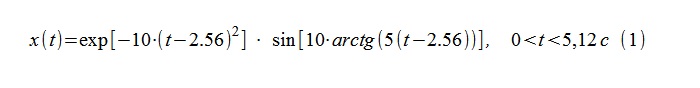
"Logarithmic" and the subsequent differentiation, respectively, of high-frequency filling and the envelope from (1), obtained theoretical expressions for (instantaneous) frequency and decrement (2)

For the An-modeling by the periodogram method (direct and inverse Fourier transform), the analytical signal y [i] is generated from the initial sequence x [i].

The ratio of two consecutive samples of such a signal, in principle, allows us to determine the instantaneous impedance λ, but to simplify this demonstration task - not to bother with creating intermediate samples or explaining the shift of the estimate by Δt / 2 - it was decided to work with samples “through one”, calculating λ i with respect to the subsequent y [i + 1] signal value to the previous y [i-1] (3).

For AR-modeling (second-order model), the standard procedure for calculating the autocorrelation coefficients 1, a 1i , a 2i was applied using the Yule-Walker equations, while the 5-sample sequences x [i-2], x [i -1], ... x [i + 2] (4).
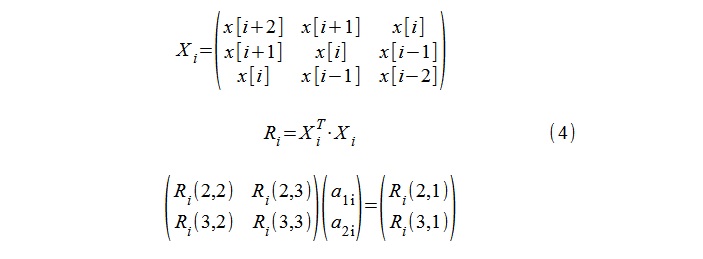
The “poles” of the λ i model are then easily calculated by the logarithm of the roots of the quadratic equation (5).
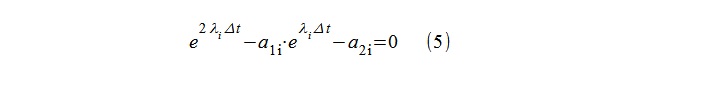

The construction of spectral estimates for the known "poles" up to a scale factor is not difficult . Further. “Instantaneous power” for the An-model is defined in an obvious way, as | y [i] | 2 , and the issue of scaling this estimate appears to have been exhausted. For the AR model, the usual technique associated with determining the power of the conventional white noise in the case of a non-stationary signal “does not work”. In the absence of the best ideas, scaling was applied, based on the average square of the corresponding 5 counts. It seems that nothing more can be done by analyzing only the 5-sample sequence. In the animation, one can see how the ARM graph of the SPM sometimes “perceptibly” fails relative to the An-score. It should be understood that the moments of the “zero crossing” for an AR-model can present difficulties not only in terms of errors with an instantaneous frequency, but also with an instantaneous amplitude, especially in the low-frequency region.
A few comments at the end.
- According to current experience, both methods usually give good results in evaluating the instantaneous frequency, at least on average (based on the sampling frequency) frequency range.
- The relatively high quality of the results of the An-method, its simplicity and ease of understanding and implementation are more than compensated for by the possible difficulties with the transformation of the process according to Gilbert. A good-quality Gilbert digital filter, especially in a wide frequency range, may have an unacceptably high order. When implementing the alternative periodogram method of this transformation, it is necessary to take into account that the Fourier transform implicitly implies the completion of the process to a periodic one. As a result, it may be necessary to explicitly complete the process by building zeros. The high quality of the results of the An-method is explained by its use of information on a very wide area of the selected point in time (strictly speaking - throughout the whole process implementation process), and this property makes it difficult to implement the method (for example, when working in real time).
- If necessary, the following measures can be recommended to improve the results of the AR method:
- Data thinning (at an excessively high sampling rate)
- An increase in the number of averages is an extension of the “point of time” neighborhood involved in the model - the construction of the track matrix X with a large number of rows.
- Increasing the order of the AR-model.
Source: https://habr.com/ru/post/453722/
All Articles