How to speed up the LZ4 release in ClickHouse
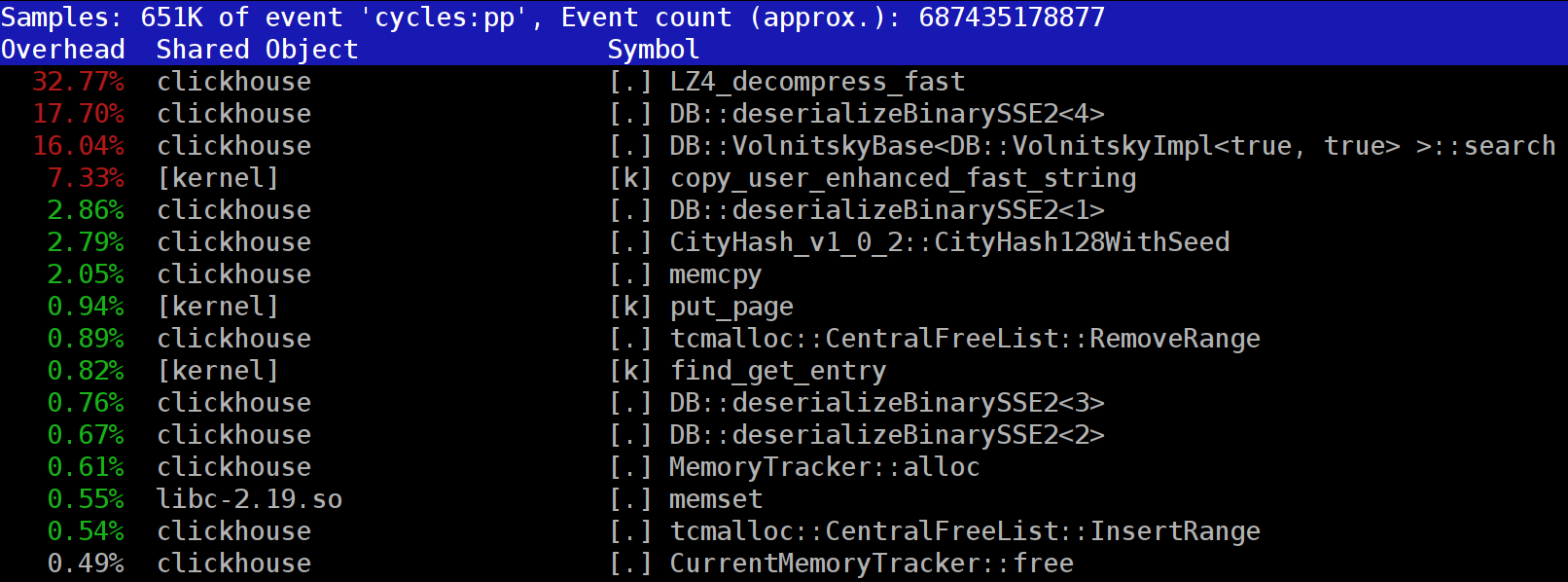
When executing queries in ClickHouse, you can note that in the profiler, LZ_decompress_fast is often visible in one of the first places. Why it happens? This question was the reason for the whole study on the choice of the best decompression algorithm. Here I publish the entire study, and the short version can be found in my report on HighLoad ++ Siberia.
The data in ClickHouse is stored in a compressed form. And during the execution of queries, ClickHouse tries to do almost nothing - use a minimum of CPU resources. It happens that all calculations for which time could be spent are already well optimized, and the query is well written by the user. Then it remains to perform the release.
')
The question is why can the LZ4 release be a bottleneck? It would seem that LZ4 is a very easy algorithm : the rate of decompression, depending on the data, is usually from 1 to 3 GB / s per processor core. This is significantly more than the speed of the disk subsystem. Moreover, we use all available cores, and decompression linearly scales across all physical cores.
But two points should be kept in mind. First, compressed data is read from the disk, and the rate of decompression is given in the amount of uncompressed data. If the compression ratio is large enough, almost nothing needs to be read from the disks. But at the same time, a lot of uncompressed data is generated, and of course, this affects the CPU consumption: the amount of work to decompress data in the case of LZ4 is almost proportional to the amount of uncompressed data.
Secondly, reading data from disks may not be required at all if the data is in cache. To do this, you can rely on page cache or use your own cache. In column DBs, using the cache is more efficient due to the fact that not all columns fall into it, but only frequently used columns. That is why LZ4 in terms of CPU load is often a bottleneck.
Hence two more questions. If the release of data "slows down", then maybe they should not be compressed at all? But in practice, this assumption is meaningless. Recently, in ClickHouse, you could configure only two options for data compression - LZ4 and Zstandard . The default is LZ4. By switching to Zstandard, you can make the compression stronger and slower. But it wasn’t quite possible to turn off compression completely until recently - LZ4 is considered as a reasonable minimum that can always be used. That is why I really love LZ4. :)
But recently, a mysterious stranger appeared in the English-speaking chat support for ClickHouse, who said that he has a very fast disk subsystem (NVMe SSD) and everything depends on compression - it would be nice to be able to turn it off. I replied that there was no such possibility, but it was easy to add. A few days later we received a pull request , which implements the
The second question that arises is: if there is a cache, why not store the already decompressed data in it? This is allowed - in many cases, it will be possible to get rid of the need for release. And in ClickHouse there is such a cache - a cache of uncompressed blocks . But it’s a pity to spend a lot of RAM because of its low efficiency. It justifies itself only on small, consecutive requests that use almost the same data.
General consideration: data should be compressed, preferably always. Always burn them to a compressed disc. Transmit over the network, too, with compression. In my opinion, the default compression should be considered justified even when transmitting on a 10-gigabit network without oversubscription within the data center, and transmitting data without compression between data centers is generally unacceptable.
Why is it used LZ4? Is it possible to pick something even lighter? In principle, it is possible, and this is right and useful. But let's first consider what class of algorithms LZ4 belongs to.
First, it does not depend on the data type. For example, if you know in advance that you will have an array of integers, you can use one of the many variants of the VarInt algorithm - this will be more efficient for the CPU. Secondly, LZ4 does not depend too much on the required assumptions for the data model. Suppose you have an ordered time series of sensor readings — an array of float numbers. Then you can calculate the deltas, and then compress further, and this will be more efficient in terms of the compression ratio.
That is, LZ4 can be used without any problems for any byte arrays - for any files. Of course, he has his own specialization (see below), and in some cases its use is meaningless. But if it is called a general purpose algorithm, it will be a small mistake. And note that, due to the internal structure, the LZ4 implements the RLE algorithm as a special case.
Another question: is LZ4 the most optimal algorithm of this class in terms of speed and compression force? Such algorithms are called pareto frontier - this means that there is no other algorithm that is strictly better in one indicator and not worse in others (and even on a wide variety of datasets). There are algorithms that are faster, but give a smaller compression ratio, and there are those that compress more, but at the same time more slowly compress or decompress.
In fact, the LZ4 is not a pareto frontier. There are options that are slightly better. For example, this is LZTURBO from some powturbo . There is no doubt about the reliability of the results thanks to the community on encode.ru (the largest and roughly the only data compression forum). But the developer does not distribute either the source code or the binaries, but only gives them to a limited circle of people for testing or for a lot of money (like no one has yet paid). Also pay attention to the Lizard (formerly LZ5) and Density . They may work a little better than LZ4 when choosing some level of compression. Also pay attention to LZSSE - a very interesting thing. However, it is better to look at it after reading this article.
Let's take a look at how LZ4 works. This is one of the implementations of the LZ77 algorithm: L and Z indicate the authors' names (Lempel and Ziv), and 77 - for 1977, when the algorithm was published. It has many other implementations: QuickLZ, FastLZ, BriefLZ, LZF, LZO, as well as gzip and zip when using low compression levels.
Compressed using LZ4 data block contains a sequence of records (commands, instructions) of two types:
Example. Before compression:
After compression:
If we take a compressed block and walk through it with the cursor, executing these commands, we will get the initial, decompressed data as a result.
We have looked at how data is expanded. The essence is also clear: to perform compression, the algorithm encodes repeated sequences of bytes using matches.
Clear and some properties. This algorithm is byte-oriented - it does not dissect individual bytes, but only copies them entirely. Here lies the difference, for example, from entropy coding. For example, zstd is a composition of LZ77 and entropy coding.
Note that the size of the compressed block is chosen not too large, so as not to spend a lot of RAM during decompression; not to slow down the random access in a compressed file (which consists of many compressed blocks); and sometimes, in order for the block to fit in some CPU cache. For example, you can choose 64 KB - so the buffers for compressed and uncompressed data will fit into the L2-cache and half still remain.
If we need to compress a larger file, we will simply concatenate the compressed blocks. At the same time, it is convenient to arrange additional data next to each compressed block - dimensions, check-sum.
The maximum offset for the match is limited, in LZ4 - 64 kilobytes. This value is called the sliding window. Indeed, this means that as the cursor moves forward, coincidences may be in a 64 kilobyte window to the cursor that moves with the cursor.
Now let's look at how to compress the data — in other words, how to find matching sequences in the file. Of course, you can use suffix trie (great if you've heard of it). There are options in which the longest matching sequence is guaranteed among the previous bytes in the compression process. This is called optimal parsing and gives almost the best compression ratio for a fixed format of a compressed block. But there are more efficient options - when we find some fairly good match in the data, but not necessarily the longest. The most effective way to find it is to use a hash table.
To do this, we go through the source data block with the cursor and take a few bytes after the cursor. For example, 4 bytes. Hash them and put in the hash table the offset from the beginning of the block - where these 4 bytes met. The value of 4 is called min-match - using such a hash table we can find a match of at least 4 bytes.
If we looked at the hash table, and there is already a record, and if the offset does not exceed the sliding window, then we check how many more bytes match after these four bytes. Maybe there is still a lot of things the same. It is also possible that there is a collision in the hash table and nothing matches. This is normal - you can simply replace the value in the hash table with a new one. Collisions in the hash table will simply result in a lower compression ratio, since there are fewer matches. By the way, this kind of hash tables (fixed size and without collision resolution) is called a cache table, a cache table. This is also logical - in the event of a collision, the cache table simply forgets about the old record.
So, I want to speed up the LZ4 release. Let's see what the decompression cycle is. Here is the loop in pseudocode:
The LZ4 format is designed so that literals and matches alternate in a compressed file. And obviously, literal always goes first (because from the very beginning there is no place to take the match). Therefore, their lengths are encoded together.
In fact, everything is a little more complicated. One byte is read from the file, and two halves (nibble) are taken from it, in which the numbers from 0 to 15 are encoded. If the corresponding number is not 15, then it is considered the length of the literal and the match, respectively. And if it is 15, then the length is longer and it is encoded in the following bytes. Then the next byte is read, and its value is added to the length. Further, if it is equal to 255, then we continue - we read the next byte in the same way.
Note that the maximum compression ratio for the LZ4 format does not reach 255. And the second (useless) observation: if your data is very redundant, then using LZ4 twice will increase the compression ratio.
When we read the length of the literal (and then also the length of the match and the offset of the match), to decompress, simply copy two fragments of memory.
It would seem that you can use the
Why use the memcpy function is not optimal? Because she:
The last point is the most important. Suppose we asked the memcpy function to copy exactly 5 bytes. It would be very good to copy 8 bytes at once, using two movq instructions for this.
But then we will copy three extra bytes - that is, we will write abroad the transferred buffer. The
But in our case, we can almost always write extra bytes. We can read extra bytes in the input-buffer as long as the extra bytes are located entirely in it. Under the same conditions, we can write extra bytes into the output buffer - because at the next iteration we will overwrite them anyway.
This optimization is already in the original implementation of LZ4:
To take advantage of this optimization, you only need to check that we are far enough away from the buffer boundary. This should be free of charge, because we are already checking for a buffer overflow. And the processing of the last few bytes - the "tail" of the data - can be done after the main loop.
However, there are still some subtleties. In the cycle of two copies - literal and match. But when using the LZ4_decompress_fast function (instead of LZ4_decompress_safe), the check is performed once - when we need to copy the literal. When copying a match, the check is not performed, but in the LZ4 format specification itself there are conditions that allow it to be avoided:
Specially selected input data may cause a “trip” from memory. If you use the LZ4_decompress_fast function, you need protection against bad data. Compressed data should be at least check-summarized. And if you need protection from an attacker, then use the function LZ4_decompress_safe. Other options: take a cryptographic hash function as a check-sum, but it will almost surely kill all performance; or allocate more memory for buffers; or allocate memory for buffers with a separate mmap call and create a guard page.
When I see the code that copies data by 8 bytes, I immediately ask - and why precisely 8 bytes? You can copy 16 bytes using SSE registers:
Copying of 32 bytes for AVX and 64 bytes for AVX-512 works in a similar way. In addition, you can expand the cycle several times. If you have ever looked at how
Why is this not done in the original LZ4 implementation? Firstly, it is not obvious whether it is better or worse. The result depends on the size of the fragments that you want to copy. Suddenly they are all short and unnecessary work will come to nothing? And secondly, it destroys those conditions in the LZ4 format, which allow to avoid unnecessary brunch in the internal cycle.
Nevertheless, we will keep this option in mind for now.
Let's return to the question - is it always possible to copy data in this way? Suppose we need to copy a match — that is, copy a fragment of memory from the output buffer located at some offset behind the cursor to the position of this cursor.
Imagine a simple case - you need to copy 5 bytes at an offset of 12:
But there is a more complicated case - when we need to copy a fragment of memory whose length is greater than the offset. That is, it partially indicates data that has not yet been written to the output buffer.
Copy 10 bytes at offset 3:
In the process of compression, we have all the data, and such a match could very well be found. The
Here's how it works:
That is, we have to create a repeating sequence. In the original LZ4 implementation, surprisingly incomprehensible code was written for this:
We copy the first 4 bytes byte by one, shift to some magic number, copy the next 4 bytes entirely, move the pointer to match to another magic number. For some ridiculous reason, the author of the code ( Ian Collet ) forgot to leave a comment about what it means. In addition, variable names are confusing. Both are called dec ... table, but we add one of them and subtract the other. In addition, one of them is unsigned, and the other is int. , : .
. 4 :
4 :
, 8 :
, — . Here's what happened:
, , . , , — 16 .
« » , (
? , SIMD-, 16 , ( 1 15). , , .
—
:
— ! :
, ? SSSE3 — , 2006 . AVX2 , 32 , 16- . packed shuffle bytes, vector permute bytes — , . AVX-512 VBMI , 64 , . ARM NEON — vtbl (vector table lookup), 8 .
,
Highload++ Siberia , 8 ( ) — !
, , 16 . ?
, . , , , . , .
, . , , , 65 536 . 65 536 . , , 65 551 . , , 96 128 — . , «» mmap ( madvice). - page faults. , .
, , :
.
Example 1:
Xeon E2650v2, ., AppVersion.
reference: 1.67 GB/sec.
16 bytes, shuffle: 2.94 GB/sec ( 76% ).
Example 2:
Xeon E2650v2, ., ShowsSumPosition.
reference: 2.30 GB/sec.
16 bytes, shuffle: 1.91 GB/sec ( 20% ).
, . , . - , . , . — 16 . : , , .
, C++ : 8- 16- ; shuffle-.
, shuffle . , :
«» (c Xeon E5645), , . , , . , shuffle-, , 16- .
:
. thermal throttling power capping.
, , . , , . . , , . : ClickHouse , , . , ( — ?). .
, , . « » . , , , .
, . . - . — ClickHouse 64 . ( .)
, « », , . , , , - . . , , . .
, , . «» , . , . Thompson Sampling.
, , . — : , . . , . , C++. — , - , ; .
? , . . -, , . -, , , «» .
, , Thompson Sampling — ( , ). , , - , , . , .
, «» . , , «», . — . , , .
, , , , «»:
, — memory latencies.
, , — LZ4 .
, :
— reference (baseline): LZ4 ;
— variant 0: 8 , shuffle;
— variant 1: 8 , shuffle;
— variant 2: 16 , shuffle;
— variant 3: 16 , shuffle;
— «» , .
CPU, , . , CPU ?
ClickHouse , 256 100 ( 256 ). , CPU , . CPU:
— Intel® Xeon® CPU E5-2650 v2 @ 2.60GHz
— Intel® Xeon® CPU E5-2660 v4 @ 2.00GHz
— Intel® Xeon® CPU E5-2660 0 @ 2.20GHz
— Intel® Xeon® CPU E5645 @ 2.40GHz
— Intel Xeon E312xx (Sandy Bridge)
— AMD Opteron(TM) Processor 6274
— AMD Opteron(tm) Processor 6380
— Intel® Xeon® CPU E5-2683 v4 @ 2.10GHz
— Intel® Xeon® CPU E5530 @ 2.40GHz
— Intel® Xeon® CPU E5440 @ 2.83GHz
— Intel® Xeon® CPU E5-2667 v2 @ 3.30GHz
— , R&D:
— AMD EPYC 7351 16-Core Processor — AMD.
— Cavium ThunderX2 — x86, AArch64. SIMD- . 224 56 .
13 , 256 6 (reference, 0, 1, 2, 3, adaptive), 10 , . 199 680 , .
, CPU . : LZ4 ( — ). , Cavium . ClickHouse, «» Xeon E5-2650 v2 , , ClickHouse x86.
ref, adapt, max — (, ). best — , 0 3. adapt_boost — baseline. max_boost — baseline. adapt_over_max — .
, x86 12–20%. ARM 4%, , . , «» Intel.
. , LZ4 12–20%, . . , .
, , «» , ZStandard level 1 LZ4: IO .
— , . , .
: . LZ4 , Lizard, Density LZSSE , . , LZ4 LZSSE ClickHouse.
LZ4 : . : , . . , inc- dec- . , 12–15% 32 , 16, . 32 — , .
, , page cache userspace ( mmap, O_DIRECT userspace page cache — ), - ( CityHash128 CRC32-C, HighwayHash, FARSH XXH3). , .
, master, . HighLoad++ Siberia, .
The data in ClickHouse is stored in a compressed form. And during the execution of queries, ClickHouse tries to do almost nothing - use a minimum of CPU resources. It happens that all calculations for which time could be spent are already well optimized, and the query is well written by the user. Then it remains to perform the release.

')
The question is why can the LZ4 release be a bottleneck? It would seem that LZ4 is a very easy algorithm : the rate of decompression, depending on the data, is usually from 1 to 3 GB / s per processor core. This is significantly more than the speed of the disk subsystem. Moreover, we use all available cores, and decompression linearly scales across all physical cores.
But two points should be kept in mind. First, compressed data is read from the disk, and the rate of decompression is given in the amount of uncompressed data. If the compression ratio is large enough, almost nothing needs to be read from the disks. But at the same time, a lot of uncompressed data is generated, and of course, this affects the CPU consumption: the amount of work to decompress data in the case of LZ4 is almost proportional to the amount of uncompressed data.
Secondly, reading data from disks may not be required at all if the data is in cache. To do this, you can rely on page cache or use your own cache. In column DBs, using the cache is more efficient due to the fact that not all columns fall into it, but only frequently used columns. That is why LZ4 in terms of CPU load is often a bottleneck.
Hence two more questions. If the release of data "slows down", then maybe they should not be compressed at all? But in practice, this assumption is meaningless. Recently, in ClickHouse, you could configure only two options for data compression - LZ4 and Zstandard . The default is LZ4. By switching to Zstandard, you can make the compression stronger and slower. But it wasn’t quite possible to turn off compression completely until recently - LZ4 is considered as a reasonable minimum that can always be used. That is why I really love LZ4. :)
But recently, a mysterious stranger appeared in the English-speaking chat support for ClickHouse, who said that he has a very fast disk subsystem (NVMe SSD) and everything depends on compression - it would be nice to be able to turn it off. I replied that there was no such possibility, but it was easy to add. A few days later we received a pull request , which implements the
none compression method. I asked for the results - how much it helped, how much the queries accelerated. The man said that this new feature was useless in practice, because the data without compression began to take up too much space.The second question that arises is: if there is a cache, why not store the already decompressed data in it? This is allowed - in many cases, it will be possible to get rid of the need for release. And in ClickHouse there is such a cache - a cache of uncompressed blocks . But it’s a pity to spend a lot of RAM because of its low efficiency. It justifies itself only on small, consecutive requests that use almost the same data.
General consideration: data should be compressed, preferably always. Always burn them to a compressed disc. Transmit over the network, too, with compression. In my opinion, the default compression should be considered justified even when transmitting on a 10-gigabit network without oversubscription within the data center, and transmitting data without compression between data centers is generally unacceptable.
Why LZ4
Why is it used LZ4? Is it possible to pick something even lighter? In principle, it is possible, and this is right and useful. But let's first consider what class of algorithms LZ4 belongs to.
First, it does not depend on the data type. For example, if you know in advance that you will have an array of integers, you can use one of the many variants of the VarInt algorithm - this will be more efficient for the CPU. Secondly, LZ4 does not depend too much on the required assumptions for the data model. Suppose you have an ordered time series of sensor readings — an array of float numbers. Then you can calculate the deltas, and then compress further, and this will be more efficient in terms of the compression ratio.
That is, LZ4 can be used without any problems for any byte arrays - for any files. Of course, he has his own specialization (see below), and in some cases its use is meaningless. But if it is called a general purpose algorithm, it will be a small mistake. And note that, due to the internal structure, the LZ4 implements the RLE algorithm as a special case.
Another question: is LZ4 the most optimal algorithm of this class in terms of speed and compression force? Such algorithms are called pareto frontier - this means that there is no other algorithm that is strictly better in one indicator and not worse in others (and even on a wide variety of datasets). There are algorithms that are faster, but give a smaller compression ratio, and there are those that compress more, but at the same time more slowly compress or decompress.
In fact, the LZ4 is not a pareto frontier. There are options that are slightly better. For example, this is LZTURBO from some powturbo . There is no doubt about the reliability of the results thanks to the community on encode.ru (the largest and roughly the only data compression forum). But the developer does not distribute either the source code or the binaries, but only gives them to a limited circle of people for testing or for a lot of money (like no one has yet paid). Also pay attention to the Lizard (formerly LZ5) and Density . They may work a little better than LZ4 when choosing some level of compression. Also pay attention to LZSSE - a very interesting thing. However, it is better to look at it after reading this article.
How does LZ4 work
Let's take a look at how LZ4 works. This is one of the implementations of the LZ77 algorithm: L and Z indicate the authors' names (Lempel and Ziv), and 77 - for 1977, when the algorithm was published. It has many other implementations: QuickLZ, FastLZ, BriefLZ, LZF, LZO, as well as gzip and zip when using low compression levels.
Compressed using LZ4 data block contains a sequence of records (commands, instructions) of two types:
- Literals (literals): "take the following N bytes as they are and copy them into the result."
- Match (match, match): "take N bytes, which were already in the decompressed result at offset offset from the current position."
Example. Before compression:
Hello world HelloAfter compression:
literals 12 "Hello world " match 5 12If we take a compressed block and walk through it with the cursor, executing these commands, we will get the initial, decompressed data as a result.
We have looked at how data is expanded. The essence is also clear: to perform compression, the algorithm encodes repeated sequences of bytes using matches.
Clear and some properties. This algorithm is byte-oriented - it does not dissect individual bytes, but only copies them entirely. Here lies the difference, for example, from entropy coding. For example, zstd is a composition of LZ77 and entropy coding.
Note that the size of the compressed block is chosen not too large, so as not to spend a lot of RAM during decompression; not to slow down the random access in a compressed file (which consists of many compressed blocks); and sometimes, in order for the block to fit in some CPU cache. For example, you can choose 64 KB - so the buffers for compressed and uncompressed data will fit into the L2-cache and half still remain.
If we need to compress a larger file, we will simply concatenate the compressed blocks. At the same time, it is convenient to arrange additional data next to each compressed block - dimensions, check-sum.
The maximum offset for the match is limited, in LZ4 - 64 kilobytes. This value is called the sliding window. Indeed, this means that as the cursor moves forward, coincidences may be in a 64 kilobyte window to the cursor that moves with the cursor.
Now let's look at how to compress the data — in other words, how to find matching sequences in the file. Of course, you can use suffix trie (great if you've heard of it). There are options in which the longest matching sequence is guaranteed among the previous bytes in the compression process. This is called optimal parsing and gives almost the best compression ratio for a fixed format of a compressed block. But there are more efficient options - when we find some fairly good match in the data, but not necessarily the longest. The most effective way to find it is to use a hash table.
To do this, we go through the source data block with the cursor and take a few bytes after the cursor. For example, 4 bytes. Hash them and put in the hash table the offset from the beginning of the block - where these 4 bytes met. The value of 4 is called min-match - using such a hash table we can find a match of at least 4 bytes.
If we looked at the hash table, and there is already a record, and if the offset does not exceed the sliding window, then we check how many more bytes match after these four bytes. Maybe there is still a lot of things the same. It is also possible that there is a collision in the hash table and nothing matches. This is normal - you can simply replace the value in the hash table with a new one. Collisions in the hash table will simply result in a lower compression ratio, since there are fewer matches. By the way, this kind of hash tables (fixed size and without collision resolution) is called a cache table, a cache table. This is also logical - in the event of a collision, the cache table simply forgets about the old record.
Task for the attentive reader. Let the data be an array of UInt32 type in little endian format, which is part of the sequence of natural numbers: 0, 1, 2 ... Explain why using LZ4 does not compress this data (the amount of compressed data is no less than the amount of uncompressed data).
How to speed things up
So, I want to speed up the LZ4 release. Let's see what the decompression cycle is. Here is the loop in pseudocode:
while (...)
{
read (input_pos, literal_length, match_length);
copy (output_pos, input_pos, literal_length);
output_pos + = literal_length;
read (input_pos, match_offset);
copy (output_pos, output_pos - match_offset,
match_length);
output_pos + = match_length;
} The LZ4 format is designed so that literals and matches alternate in a compressed file. And obviously, literal always goes first (because from the very beginning there is no place to take the match). Therefore, their lengths are encoded together.
In fact, everything is a little more complicated. One byte is read from the file, and two halves (nibble) are taken from it, in which the numbers from 0 to 15 are encoded. If the corresponding number is not 15, then it is considered the length of the literal and the match, respectively. And if it is 15, then the length is longer and it is encoded in the following bytes. Then the next byte is read, and its value is added to the length. Further, if it is equal to 255, then we continue - we read the next byte in the same way.
Note that the maximum compression ratio for the LZ4 format does not reach 255. And the second (useless) observation: if your data is very redundant, then using LZ4 twice will increase the compression ratio.
When we read the length of the literal (and then also the length of the match and the offset of the match), to decompress, simply copy two fragments of memory.
How to copy a piece of memory
It would seem that you can use the
memcpy function, which is just meant for copying fragments of memory. But this is not optimal and still incorrect.Why use the memcpy function is not optimal? Because she:
- usually located in the libc library (and the libc library is usually linked dynamically, and the call to memcpy will go indirectly through the PLT),
- does not inline with the size argument unknown to compile time,
- makes a lot of effort for correct processing of the “tails” of a fragment of memory that are not multiples of the size of a machine word or register
The last point is the most important. Suppose we asked the memcpy function to copy exactly 5 bytes. It would be very good to copy 8 bytes at once, using two movq instructions for this.
Hello world Hello wo ...
^^^^^ ^^^ - src
^^^^^ ^^^ - dstBut then we will copy three extra bytes - that is, we will write abroad the transferred buffer. The
memcpy function does not have the right to do this - indeed, because we will overwrite some data in our program, there will be a “passage” from memory. And if we wrote to an unaligned address, then these extra bytes can be located on an unallocated page of virtual memory or on a page without write access. Then we get a segfault (this is good).But in our case, we can almost always write extra bytes. We can read extra bytes in the input-buffer as long as the extra bytes are located entirely in it. Under the same conditions, we can write extra bytes into the output buffer - because at the next iteration we will overwrite them anyway.
This optimization is already in the original implementation of LZ4:
inline void copy8 (UInt8 * dst, const UInt8 * src)
{
memcpy (dst, src, 8); /// Actually, memcpy is not called here.
}
inline void wildCopy8 (UInt8 * dst, const UInt8 * src, UInt8 * dst_end)
{
do
{
copy8 (dst, src);
dst + = 8;
src + = 8;
} while (dst <dst_end);
} To take advantage of this optimization, you only need to check that we are far enough away from the buffer boundary. This should be free of charge, because we are already checking for a buffer overflow. And the processing of the last few bytes - the "tail" of the data - can be done after the main loop.
However, there are still some subtleties. In the cycle of two copies - literal and match. But when using the LZ4_decompress_fast function (instead of LZ4_decompress_safe), the check is performed once - when we need to copy the literal. When copying a match, the check is not performed, but in the LZ4 format specification itself there are conditions that allow it to be avoided:
The last 5 bytes are always literals
By the end of the block.
Consequently, a block with less than 13 bytes cannot be compressed.
Specially selected input data may cause a “trip” from memory. If you use the LZ4_decompress_fast function, you need protection against bad data. Compressed data should be at least check-summarized. And if you need protection from an attacker, then use the function LZ4_decompress_safe. Other options: take a cryptographic hash function as a check-sum, but it will almost surely kill all performance; or allocate more memory for buffers; or allocate memory for buffers with a separate mmap call and create a guard page.
When I see the code that copies data by 8 bytes, I immediately ask - and why precisely 8 bytes? You can copy 16 bytes using SSE registers:
inline void copy16 (UInt8 * dst, const UInt8 * src)
{
#if __SSE2__
_mm_storeu_si128 (reinterpret_cast <__ m128i *> (dst),
_mm_loadu_si128 (reinterpret_cast <const __m128i *> (src)));
#else
memcpy (dst, src, 16);
#endif
}
inline void wildCopy16 (UInt8 * dst, const UInt8 * src, UInt8 * dst_end)
{
do
{
copy16 (dst, src);
dst + = 16;
src + = 16;
} while (dst <dst_end);
} Copying of 32 bytes for AVX and 64 bytes for AVX-512 works in a similar way. In addition, you can expand the cycle several times. If you have ever looked at how
memcpy implemented, then this is exactly the approach. (By the way, the compiler in this case will neither expand nor vectorize the cycle: this will require the insertion of cumbersome checks.)Why is this not done in the original LZ4 implementation? Firstly, it is not obvious whether it is better or worse. The result depends on the size of the fragments that you want to copy. Suddenly they are all short and unnecessary work will come to nothing? And secondly, it destroys those conditions in the LZ4 format, which allow to avoid unnecessary brunch in the internal cycle.
Nevertheless, we will keep this option in mind for now.
Sneaky copy
Let's return to the question - is it always possible to copy data in this way? Suppose we need to copy a match — that is, copy a fragment of memory from the output buffer located at some offset behind the cursor to the position of this cursor.
Imagine a simple case - you need to copy 5 bytes at an offset of 12:
Hello world ...........
^^^^^ - src
^^^^^ - dst
Hello world Hello wo ...
^^^^^ - src
^^^^^ - dstBut there is a more complicated case - when we need to copy a fragment of memory whose length is greater than the offset. That is, it partially indicates data that has not yet been written to the output buffer.
Copy 10 bytes at offset 3:
abc .............
^^^^^^^^^^ - src
^^^^^^^^^^ - dst
abc abcabcabca ...
^^^^^^^^^^ - src
^^^^^^^^^^ - dstIn the process of compression, we have all the data, and such a match could very well be found. The
memcpy function is not suitable for copying it: it does not support the case where the ranges of memory fragments intersect. By the way, the memmove function memmove also not suitable, because the fragment of memory, where you need to get data from, is not yet fully initialized. You need to copy as if we were copying byte-by-byte.op [0] = match [0]; op [1] = match [1]; op [2] = match [2]; op [3] = match [3]; ...
Here's how it works:
a bc a ............
^ - src
^ - dst
a b ca b ...........
^ - src
^ - dst
ab c ab c ..........
^ - src
^ - dst
abc a bc a .........
^ - src
^ - dst
abca b ca b ........
^ - src
^ - dstThat is, we have to create a repeating sequence. In the original LZ4 implementation, surprisingly incomprehensible code was written for this:
const unsigned dec32table [] = {0, 1, 2, 1, 4, 4, 4, 4};
const int dec64table [] = {0, 0, 0, -1, 0, 1, 2, 3};
const int dec64 = dec64table [offset];
op [0] = match [0];
op [1] = match [1];
op [2] = match [2];
op [3] = match [3];
match + = dec32table [offset];
memcpy (op + 4, match, 4);
match - = dec64; We copy the first 4 bytes byte by one, shift to some magic number, copy the next 4 bytes entirely, move the pointer to match to another magic number. For some ridiculous reason, the author of the code ( Ian Collet ) forgot to leave a comment about what it means. In addition, variable names are confusing. Both are called dec ... table, but we add one of them and subtract the other. In addition, one of them is unsigned, and the other is int. , : .
. 4 :
abc abca .........
^^^^ - src
^^^^ - dst4 :
abcabca bcab .....
^^^^ - src
^^^^ - dst, 8 :
abcabcabcab cabcabca .....
^^^^^^^^ - src
^^^^^^^^ - dst, — . Here's what happened:
inline void copyOverlap8(UInt8 * op, const UInt8 *& match, const size_t offset)
{
/// 4 % n.
/// Or if 4 % n is zero, we use n.
/// It gives equivalent result, but is better CPU friendly for unknown reason.
static constexpr int shift1[] = { 0, 1, 2, 1, 4, 4, 4, 4 };
/// 8 % n - 4 % n
static constexpr int shift2[] = { 0, 0, 0, 1, 0, -1, -2, -3 };
op[0] = match[0];
op[1] = match[1];
op[2] = match[2];
op[3] = match[3];
match += shift1[offset];
memcpy(op + 4, match, 4);
match += shift2[offset];
} , , . , , — 16 .
« » , (
offset < 16 , offset < 8 ). () 16- : inline void copyOverlap16(UInt8 * op, const UInt8 *& match, const size_t offset)
{
/// 4 % n.
static constexpr int shift1[]
= { 0, 1, 2, 1, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4 };
/// 8 % n - 4 % n
static constexpr int shift2[]
= { 0, 0, 0, 1, 0, -1, -2, -3, -4, 4, 4, 4, 4, 4, 4, 4 };
/// 16 % n - 8 % n
static constexpr int shift3[]
= { 0, 0, 0, -1, 0, -2, 2, 1, 8, -1, -2, -3, -4, -5, -6, -7 };
op[0] = match[0];
op[1] = match[1];
op[2] = match[2];
op[3] = match[3];
match += shift1[offset];
memcpy(op + 4, match, 4);
match += shift2[offset];
memcpy(op + 8, match, 8);
match += shift3[offset];
} ? , SIMD-, 16 , ( 1 15). , , .
—
pshufb ( packed shuffle bytes) SSSE3 ( S). 16- . . — «»: 0 15 — , . , 127 — .:
xmm0: abc............. xmm1: 0120120120120120 pshufb %xmm1, %xmm0 xmm0: abcabcabcabcabca
— ! :
inline void copyOverlap16Shuffle(UInt8 * op, const UInt8 *& match, const size_t offset)
{
#ifdef __SSSE3__
static constexpr UInt8 __attribute__((__aligned__(16))) masks[] =
{
0, 1, 2, 1, 4, 1, 4, 2, 8, 7, 6, 5, 4, 3, 2, 1, /* offset = 0, not used as mask, but for shift amount instead */
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, /* offset = 1 */
0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1,
0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, 2, 0,
0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3,
0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0,
0, 1, 2, 3, 4, 5, 0, 1, 2, 3, 4, 5, 0, 1, 2, 3,
0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4, 5, 6, 0, 1,
0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2, 3, 4, 5, 6, 7,
0, 1, 2, 3, 4, 5, 6, 7, 8, 0, 1, 2, 3, 4, 5, 6,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0, 1, 2, 3, 4,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 0, 1, 2, 3,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 0, 1, 2,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 0, 1,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 0,
};
_mm_storeu_si128(reinterpret_cast<__m128i *>(op),
_mm_shuffle_epi8(
_mm_loadu_si128(reinterpret_cast<const __m128i *>(match)),
_mm_load_si128(reinterpret_cast<const __m128i *>(masks) + offset)));
match += masks[offset];
#else
copyOverlap16(op, match, offset);
#endif
} _mm_shuffle_epi8 — intrinsic , pshufb ., ? SSSE3 — , 2006 . AVX2 , 32 , 16- . packed shuffle bytes, vector permute bytes — , . AVX-512 VBMI , 64 , . ARM NEON — vtbl (vector table lookup), 8 .
,
pshufb 64- MMX-, 8 . . , , 16 ( ).Highload++ Siberia , 8 ( ) — !
if
, , 16 . ?
, . , , , . , .
, . , , , 65 536 . 65 536 . , , 65 551 . , , 96 128 — . , «» mmap ( madvice). - page faults. , .
?
, , :
- 16 8.
- shuffle-
offset < 16. - if.
.
Example 1:
Xeon E2650v2, ., AppVersion.
reference: 1.67 GB/sec.
16 bytes, shuffle: 2.94 GB/sec ( 76% ).
Example 2:
Xeon E2650v2, ., ShowsSumPosition.
reference: 2.30 GB/sec.
16 bytes, shuffle: 1.91 GB/sec ( 20% ).
, . , . - , . , . — 16 . : , , .
, C++ : 8- 16- ; shuffle-.
template <size_t copy_amount, bool use_shuffle>
void NO_INLINE decompressImpl(
const char * const source,
char * const dest,
size_t dest_size) , shuffle . , :
sudo echo 'performance' | tee /sys/devices/system/cpu/cpu*/cpufreq/scaling_governor kill -STOP $(pidof firefox) $(pidof chromium)
«» (c Xeon E5645), , . , , . , shuffle-, , 16- .
:
sudo kill -STOP $(pidof python) $(pidof perl) $(pgrep -u skynet) $(pidof cqudp-client)
. thermal throttling power capping.
, , . , , . . , , . : ClickHouse , , . , ( — ?). .
, , . « » . , , , .
, . . - . — ClickHouse 64 . ( .)
, « », , . , , , - . . , , . .
, , . «» , . , . Thompson Sampling.
, , . — : , . . , . , C++. — , - , ; .
? , . . -, , . -, , , «» .
, , Thompson Sampling — ( , ). , , - , , . , .
, «» . , , «», . — . , , .
, , , , «»:
/// For better convergence, we don't use proper estimate of stddev.
/// We want to eventually separate between two algorithms even in case
/// when there is no statistical significant difference between them.
double sigma() const
{
return mean() / sqrt(adjustedCount());
}
double sample(pcg64 & rng) const
{
...
return std::normal_distribution<>(mean(), sigma())(rng);
} , — memory latencies.
, , — LZ4 .
, :
— reference (baseline): LZ4 ;
— variant 0: 8 , shuffle;
— variant 1: 8 , shuffle;
— variant 2: 16 , shuffle;
— variant 3: 16 , shuffle;
— «» , .
CPU
CPU, , . , CPU ?
ClickHouse , 256 100 ( 256 ). , CPU , . CPU:
— Intel® Xeon® CPU E5-2650 v2 @ 2.60GHz
— Intel® Xeon® CPU E5-2660 v4 @ 2.00GHz
— Intel® Xeon® CPU E5-2660 0 @ 2.20GHz
— Intel® Xeon® CPU E5645 @ 2.40GHz
— Intel Xeon E312xx (Sandy Bridge)
— AMD Opteron(TM) Processor 6274
— AMD Opteron(tm) Processor 6380
— Intel® Xeon® CPU E5-2683 v4 @ 2.10GHz
— Intel® Xeon® CPU E5530 @ 2.40GHz
— Intel® Xeon® CPU E5440 @ 2.83GHz
— Intel® Xeon® CPU E5-2667 v2 @ 3.30GHz
— , R&D:
— AMD EPYC 7351 16-Core Processor — AMD.
— Cavium ThunderX2 — x86, AArch64. SIMD- . 224 56 .
13 , 256 6 (reference, 0, 1, 2, 3, adaptive), 10 , . 199 680 , .
, CPU . : LZ4 ( — ). , Cavium . ClickHouse, «» Xeon E5-2650 v2 , , ClickHouse x86.
┌─cpu───────────────────┬──ref─┬─adapt─┬──max─┬─best─┬─adapt_boost─┬─max_boost─┬─adapt_over_max─┐ │ E5-2667 v2 @ 3.30GHz │ 2.81 │ 3.19 │ 3.15 │ 3 │ 1.14 │ 1.12 │ 1.01 │ │ E5-2650 v2 @ 2.60GHz │ 2.5 │ 2.84 │ 2.81 │ 3 │ 1.14 │ 1.12 │ 1.01 │ │ E5-2683 v4 @ 2.10GHz │ 2.26 │ 2.63 │ 2.59 │ 3 │ 1.16 │ 1.15 │ 1.02 │ │ E5-2660 v4 @ 2.00GHz │ 2.15 │ 2.49 │ 2.46 │ 3 │ 1.16 │ 1.14 │ 1.01 │ │ AMD EPYC 7351 │ 2.03 │ 2.44 │ 2.35 │ 3 │ 1.20 │ 1.16 │ 1.04 │ │ E5-2660 0 @ 2.20GHz │ 2.13 │ 2.39 │ 2.37 │ 3 │ 1.12 │ 1.11 │ 1.01 │ │ E312xx (Sandy Bridge) │ 1.97 │ 2.2 │ 2.18 │ 3 │ 1.12 │ 1.11 │ 1.01 │ │ E5530 @ 2.40GHz │ 1.65 │ 1.93 │ 1.94 │ 3 │ 1.17 │ 1.18 │ 0.99 │ │ E5645 @ 2.40GHz │ 1.65 │ 1.92 │ 1.94 │ 3 │ 1.16 │ 1.18 │ 0.99 │ │ AMD Opteron 6380 │ 1.47 │ 1.58 │ 1.56 │ 1 │ 1.07 │ 1.06 │ 1.01 │ │ AMD Opteron 6274 │ 1.15 │ 1.35 │ 1.35 │ 1 │ 1.17 │ 1.17 │ 1 │ │ E5440 @ 2.83GHz │ 1.35 │ 1.33 │ 1.42 │ 1 │ 0.99 │ 1.05 │ 0.94 │ │ Cavium ThunderX2 │ 0.84 │ 0.87 │ 0.87 │ 0 │ 1.04 │ 1.04 │ 1 │ └───────────────────────┴──────┴───────┴──────┴──────┴─────────────┴───────────┴────────────────┘
ref, adapt, max — (, ). best — , 0 3. adapt_boost — baseline. max_boost — baseline. adapt_over_max — .
, x86 12–20%. ARM 4%, , . , «» Intel.
findings
. , LZ4 12–20%, . . , .
, , «» , ZStandard level 1 LZ4: IO .
— , . , .
: . LZ4 , Lizard, Density LZSSE , . , LZ4 LZSSE ClickHouse.
LZ4 : . : , . . , inc- dec- . , 12–15% 32 , 16, . 32 — , .
, , page cache userspace ( mmap, O_DIRECT userspace page cache — ), - ( CityHash128 CRC32-C, HighwayHash, FARSH XXH3). , .
, master, . HighLoad++ Siberia, .
Source: https://habr.com/ru/post/452778/
All Articles