Complex systems. Critical level
If you spend some time thinking about complex systems, you probably understand the importance of networking. Networks rule our world. From chemical reactions within the cell to the network of relationships in the ecosystem, trade and political networks that shape the course of history.
Or consider this article you are reading. You probably found it on a social network , downloaded it from a computer network and are currently deciphering the meaning with the help of your neural network .
But no matter how much I thought about networks over the years, until recently I did not understand the importance of simple diffusion .
')
This is our topic for today: how, how chaotic everything moves and spreads. Some examples to whet your appetite:
A brief note about the form.
Unlike all my previous works, this essay is interactive. The original article contains interactive examples with sliders and buttons that control objects on the screen - approx. lane]
So let's get started. The first task is to develop a visual dictionary for distribution across networks.
I am sure that you all know the basis of networks, that is, nodes + edges. To explore diffusion, one need only mark some nodes as active . Or, as epidemiologists like to say, are infected :

This activation or infection spreads across the network from node to node according to the rules we develop below.
Real networks are usually much larger than this simple network of seven nodes. They are also much more confusing. But for simplicity, we will build a toy model here to study the lattice, that is, the lattice network.
(The fact that the grid lacks realism is compensated by the fact that it is easy to draw;)
Except where otherwise indicated, there are four neighbors in the network nodes, for example:
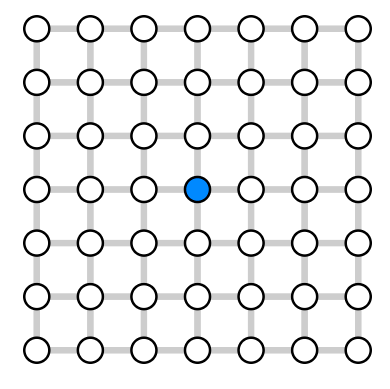
And you need to imagine that these grids stretch endlessly in all directions. In other words, we are not interested in behavior that occurs only at the edges of the network or in small populations.
Given that the grids are so ordered, you can simplify them to pixels. For example, these two images represent the same network:

In one of the behaviors, the active node always passes the infection to its (uninfected) neighbors. But it is boring. Much more interesting things happen when transmission is probabilistic .
In the SIR (Susceptible-Infected-Removed) model, the node can be in three states:
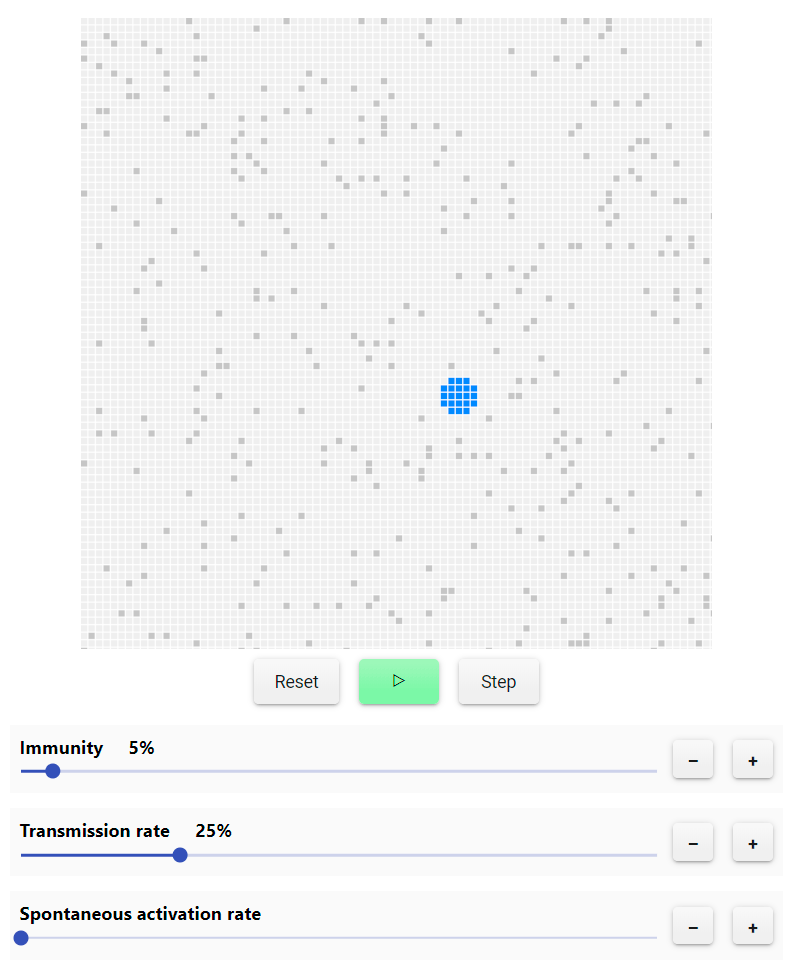
Here's how interactive simulation works [in the original article, you can choose the transmission rate of infection from 0 to 1, see the process step by step or as a whole - approx. lane]:
In the context of the disease, removal may mean that the person has died or that he has developed immunity to the pathogen. We say that they are “removed” from the simulation, because nothing happens to them anymore.
Depending on what we are trying to model, you may need another model other than SIR.
If we mimic the spread of measles or an outbreak of a forest fire, SIR fits perfectly. But suppose that we imitate the spread of a new cultural practice, such as meditation. At first, the node (person) is susceptible, because it has never done this before. Then, if he starts meditating (perhaps, having heard about it from a friend), we will model him as an infected one. But if he stops the practice, he will not die and will not fall out of the simulation, because in the future he can easily adopt this habit again. So he goes back to a receptive state.
This is the SIS (Susceptible – Infected – Susceptible) model . In the classical model, two parameters: the transfer rate and the recovery rate. However, in the simulations for this article, I decided to simplify by lowering the recovery rate parameter. Instead, the infected node automatically returns to a susceptible state at the next time step, unless it is infected by one of its neighbors. In addition, we allow a node infected in step n to infect itself in step n + 1 with a probability equal to the transmission rate.
As you can see, this is very different from the SIR model.
Since the nodes are never removed, even a very small and limited lattice can sustain SIS infection for a long time. The infection simply jumps from node to node and returns.
Despite the differences, SIR and SIS are surprisingly interchangeable for our purposes. Therefore, for the rest of the article we will focus on SIS - mainly because it is more tenacious and, therefore, it is more interesting to work with it.
By playing around with the SIR and SIS models, you might have noticed something about the longevity of the infection. At very low transmission rates, such as 10%, the infection tends to die out. While at higher values, such as 50%, the infection remains alive and captures most of the network. If the network were infinite, we could imagine that it continues and spreads forever.
Such unlimited diffusion has many names: “viral”, “nuclear” or (in the title of this article) critical .
It turns out that there is a specific turning point that separates subcritical networks (doomed to extinction) from supercritical networks (capable of infinite growth). This tipping point is called the critical threshold , and this is a fairly common feature of diffusion processes in conventional networks.
The exact value of the critical threshold varies between networks. What is common is the presence of such a value.
[In the interactive demonstration from the original article, you can try to manually feel the critical threshold of the network by changing the value of the transmission rate. It is somewhere between 22% and 23% - approx. trans.]
At 22% (and below), the infection eventually dies out. At 23% (and above), the initial infection sometimes dies out, but in most cases it can survive and spread long enough to ensure its eternal existence.
(By the way, there is a whole scientific direction dedicated to the search for these critical thresholds for different network topologies. For a quick acquaintance, I recommend quickly scrolling through the Wikipedia article on the threshold ).
In general, this is how it works: below the critical threshold, any final infection in the network is guaranteed (with probability 1) eventually dies out. But above the critical threshold there is a probability (p> 0) that the infection will last forever, and at the same time it will extend arbitrarily far from the original place.
However, note that the supercritical network does not guarantee that the infection will last forever. In fact, it often fades away, especially in the very early stages of modeling. Let's see how this happens.
Suppose we started with one infected node and four neighbors. In the first step of modeling, an infection has 5 independent chances for spreading (including the chance to “spread” on itself in the next step):
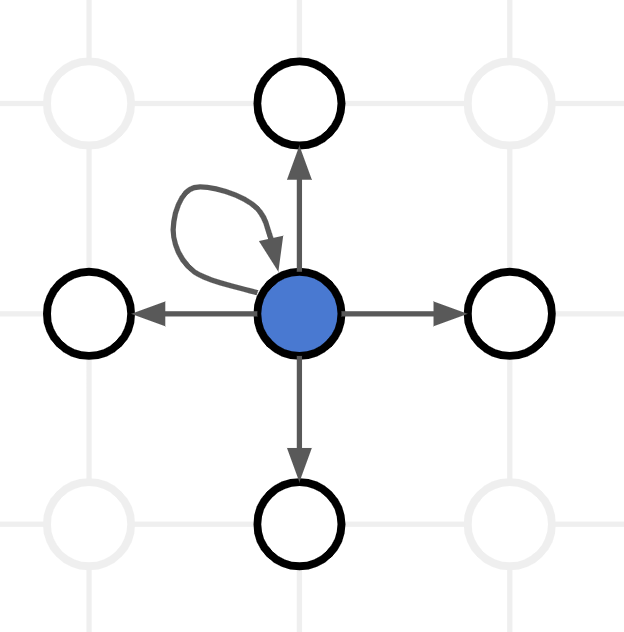
Now suppose the transfer rate is 50%. In this case, in the first step, we throw a coin five times. And if five eagles fall out, the infection will be destroyed. This happens in about 3% of cases - and this is only in the first step. An infection that has survived the first step has a certain (usually smaller) probability to die out in the second step, some (even less) probability to die out in the third step, and so on.
Thus, even when the network is supercritical - if the transmission rate is 99% - there is a chance that the infection will disappear.
But the important thing is that it will not always fade away. If you add up the probability of attenuation of all steps to infinity, the result is less than 1. In other words, with a non-zero probability, the infection will continue forever. That's what it means for a network to be supercritical.
Up to this point, all our simulations began with a small piece of pre-infected nodes in the center.
But what if to start from scratch? Then we simulate spontaneous activation — the process by which a susceptible node infects by chance (not from one of its neighbors).
This is called the SISa model . The letter “a” means “automatic.”
In the SISa simulation, a new parameter appears - the spontaneous activation rate, which changes the frequency of spontaneous infection (the transmission rate parameter that we saw earlier is also present).
What is needed for the infection to spread throughout the network?
You may have noticed in the simulation that an increase in the rate of spontaneous activation does not change whether the infection captures the entire network or not. Only the transfer rate determines whether the network is subcritical or supercritical. And when the network is subcritical (the transmission rate is less than or equal to 22%), no infection can spread to the whole grid, no matter how often it starts.
It is like lighting a fire in a wet field. You can set some dry leaves on fire, but the flame will quickly go out because the rest of the landscape does not ignite enough (subcritical). While on a very dry field (supercritical), a single spark is enough to start a raging fire.
Such things are observed in the field of ideas and inventions. Often the world is not ready for an idea, and in this case it can be reinvented again and again, but it does not catch the masses. On the other hand, the world can be fully prepared for an invention (large hidden demand), and as soon as it is born, it is accepted by all. In the middle are ideas that are invented in several places and are distributed locally, but it is not enough for any particular version to cover the entire network at once. In this latter category, we find, for example, agriculture and writing, which were independently invented by different human civilizations about ten and three times, respectively.
Suppose we make some nodes completely invulnerable, that is, immune to activation. It’s as if they were originally in a remote state, and the SIS (a) model runs on the remaining nodes.
The immunity slider controls the percentage of nodes removed. Try changing its value (while the model is running!) And see how it affects the state of the network, whether it will be supercritical or not.
Changing the number of unresponsive nodes completely changes the picture, will the network be pre- or supercritical. And it is not difficult to understand why. With a large number of unresponsive sites, the infection has fewer opportunities to spread to new hosts.
It turns out that this entails a number of very important practical consequences.
One of them is to prevent the spread of forest fires. At the local level, each person must take his own precautions (for example, never leave an open flame unattended). But on a large scale, individual flashes are inevitable. Thus, another method of protection is to ensure a sufficient number of “gaps” (in a network of flammable materials) so that the flash does not cover the entire network. This function is performed by the glades:

Another outbreak that is important to stop is an infectious disease. The concept of population immunity is introduced here. This is the idea that some people cannot be vaccinated (for example, they have an impaired immune system), but if there are enough people susceptible to the infection, the disease cannot spread forever. In other words, a sufficient part of the population should be vaccinated in order to transfer the population from the supercritical to the subcritical state. When this happens, one patient can still become infected (for example, after a trip to another region), but without a supercritical network in which to grow, the disease will infect only a handful of people.
Finally, the concept of immune sites explains what happens in a nuclear reactor. In a chain reaction, a decaying uranium-235 atom releases about three neutrons, which cause (on average) the splitting of more than one U-235 atom. New neutrons then cause further splitting of atoms and so on exponentially:

When creating a bomb, the whole point is to ensure the smooth continuation of exponential growth. But at the power plant, the goal is to produce energy without killing everyone around. For this purpose, control rods made of a material capable of absorbing neutrons (for example, silver or boron) are used. Since they absorb, rather than release, neutrons, in our simulation they act as unresponsive nodes, thereby preventing the reactor core from going to a supercritical state.
Thus, the trick of a nuclear reactor is to keep the reaction near the critical threshold, moving the control rods back and forth, and ensure that whenever something goes wrong, the rods have fallen into the core and stopped it.
The degree of a node is the number of its neighbors. Up to this point we have considered networks of the 4th degree. But what happens if you change this parameter?
For example, it is possible to connect each node not only with four direct neighbors, but also with four diagonally. In such a network the degree will be 8.
Gratings with degrees 4 and 8 are well symmetric. But with degree 5 (for example) the problem arises: which five neighbors to choose? In this case, we choose the four nearest neighbors (N, E, S, W), and then randomly select one neighbor from the set {NE, SE, SW, NW}. The choice is made independently for each node at each time step.
Again, it is not difficult to understand what is happening here. When each node has more neighbors, the chances of spreading the infection increase — and thus the network is more likely to become critical.
However, the consequences may be unexpected, as we will see below.
Until now, our networks have been completely homogeneous. Each node looks like any other. But what if we change the conditions and allow different states of nodes throughout the network?
For example, try to simulate the city. To do this, increase the density in some parts of the network (a higher degree of nodes). We do this on the basis of data that citizens have a wider social circle and more social interactions than people outside cities.
In our model, susceptible nodes are colored based on their degree. Nodes in the “countryside” have grade 4 (and are colored light gray), while nodes in the “cities” have higher degrees (and are painted darker), starting with grade 5 on the outskirts and ending at 8 in the city center .
Try to choose such a speed of propagation, so that the activation covers the cities, and then does not go beyond their borders.
I find this simulation both obvious and surprising. Of course , cities maintain a cultural level better than rural areas — everyone knows that. What surprises me is that part of this cultural diversity arises simply on the basis of the topology of the social network.
This is an interesting point, I will try to explain in more detail.
Here we are dealing with cultural forms that are transmitted simply and directly from person to person. For example, manners , salon games, fashion trends, linguistic trends, rituals of small groups and products that spread word of mouth, plus whole packets of information that we call ideas.
(Note: the dissemination of information between people is extremely complicated by the mass media. It is easier to imagine some technologically primitive environment, for example, Ancient Greece, where almost every spark of culture was transmitted by interaction in physical space).
From the above simulation, I learned that there are ideas and cultural practices that can take root and spread in the city, but they simply cannot spread in rural areas (mathematically they cannot). These are the same ideas and the same people. The point is not that the villagers have some kind of “near” ones: when interacting with the same idea, they have exactly the same chances to catch it as the citizens have. It’s just that the idea itself cannot become viral in rural areas, because there are not so many connections through which it can spread.
This is probably the easiest to see in the field of fashion - clothes, hairstyles, etc. In the network of fashion, we can fix the edge of the grid when two people notice each other's outfits. In the city center, every person can see more than 1,000 other people every day - on the street, in the subway, in a crowded restaurant, etc. In the countryside, on the contrary, each person can see only a couple of dozen others. Based only on this difference , the city is able to support more fashion trends. And only the most convincing trends - with the highest transmission speed - will be able to gain a foothold outside the city.
We tend to think that if the idea is good, then eventually it will reach everyone, and if the idea is bad, it will disappear. Of course, this is true in extreme cases, but between them there are a lot of ideas and practices that can become viral only in certain networks. This is really awesome.
We are here considering the effect of network density . It is defined for a given set of nodes as the number of actual edges divided by the number of potential edges . That is, the percentage of possible links that really exist.
So, we have seen that the density of the network in urban centers is higher than in rural areas. But cities are not the only place where we find dense networks.
An interesting example is secondary schools. For example, for a particular district, we compare the network that exists among schoolchildren with the network that exists among their parents. The same geographical area and the same population, but one network is many times denser than the other. It is therefore not surprising that fashion and linguistic tendencies spread much more quickly among adolescents.
Similarly, elite networks are usually much denser than non-elite networks — in my opinion, this fact is underestimated (people who are popular or influential spend more time creating networks, and therefore they have more “neighbors” than normal people). Based on the simulations above, we expect that elite networks will support some cultural forms that cannot be supported by the mainstream, simply on the basis of mathematical laws, by the average degree of the network. I leave you to reflect on what this may be for cultural forms.
Finally, we can apply this idea to the Internet, simulating it as a huge and very dense city. It is not surprising that many new types of culture flourish on the Internet, which are simply impossible to maintain in purely spatial networks: niche hobbies, better design standards, greater awareness of injustice, etc. And these are not only pleasant things. Just as the first cities were a breeding ground for diseases that could not spread with low population density, so the Internet is a breeding ground for malignant cultural forms, such as clickback, fake news, and incitement of artificial indignation.
We often think of discovery or invention as a process that occurs in the mind of a single genius. He is struck by a flash of inspiration and - eureka! - suddenly we get a new way to measure volume. Or the gravity equation. Or a light bulb.
But if we take the point of view of a lone inventor at the moment of discovery, then we look at the phenomenon from the point of view of a node . While it would be more correct to interpret the invention as a network phenomenon.
The network is important in at least two ways. First, already existing ideas must penetrate into the mind of the inventor. These are quotes from the new article, the bibliographic section of the new book - the giants, on whose shoulders Newton stood. Secondly, the network is crucial for bringing a new idea back into the world; an invention that has not spread can hardly be called an “invention” at all. Thus, for both these reasons, it makes sense to model the invention — or, in a broad sense, the growth of knowledge — as a process of diffusion.
In a moment, I will present a rough simulation of how knowledge within a network can spread and grow. But first I must explain.
At the beginning of the simulation, in each grid quadrant, there are four experts located as follows:
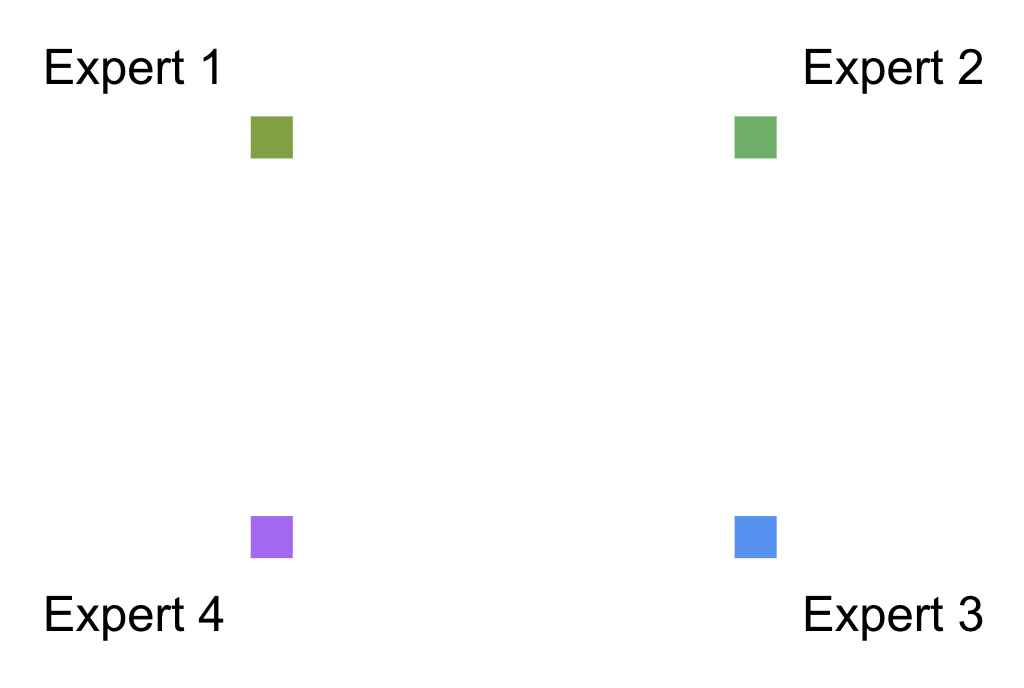
Expert 1 has the first version of the idea - let's call it Idea 1.0. Expert 2 is a person who knows how to turn Idea 1.0 into Idea 2.0. Expert 3 knows how to convert Idea 2.0 into Idea 3.0. And finally, the fourth expert knows how to make the final touches to create Idea 4.0.

This is like an origami technique, where methods are developed and combined with other methods to create more interesting designs. Or it may be a field of knowledge similar to physics, in which later work is based on the fundamental work of predecessors.
The essence of this simulation is that we need all four experts to contribute to the final version of the idea. And at each stage, the idea must be brought to the appropriate expert.
A few reservations. The simulation encoded many unrealistic assumptions. Here are just a few of them:
… and many others.
This is a ridiculously simplified model of how knowledge really grows. Outside the model there are a lot of important details (see above). Nevertheless, it reflects the important essence of the process. And therefore we can, with reservations, argue about the growth of knowledge, using our knowledge of diffusion.
In particular, the diffusion model provides an understanding of how to speed up the process : it is necessary to facilitate the exchange of ideas between expert nodes. This may mean clearing the network from dead nodes that prevent diffusion. Or it may mean the placement of all experts in a city or cluster with a large network density, where ideas quickly spread. Or just collect them in one room:
So ... that's all I can say about diffusion.
But I have one last thought, and it is very important. We are talking about the growth ( and stagnation ) of knowledge in scientific communities. This idea is different in tone and content from everything said above, but I hope you will forgive me.
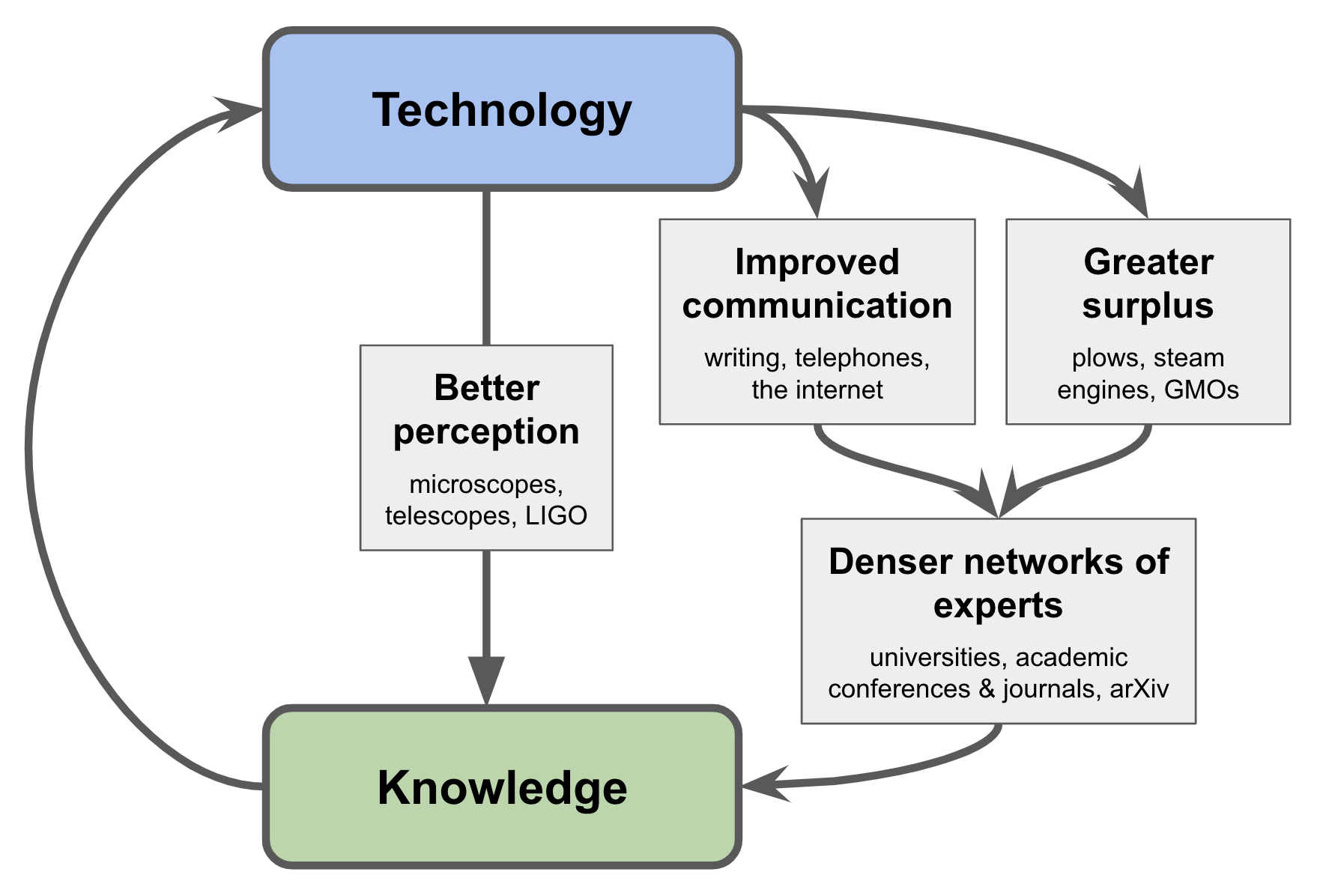
The illustration shows one of the most important positive feedback cycles in the world (and it was such a long time):

The upward cycle cycle (K ⟶ T) is quite simple: we use new knowledge to develop new tools. For example, understanding the physics of semiconductors allows us to create computers.
However, the downward movement requires some explanation. How does the development of technology lead to the growth of knowledge?
One of the ways - perhaps the most direct - is when new technologies give us new ways of perceiving the world. For example, the best microscopes allow you to take a deeper look inside the cell, throwing up ideas for molecular biology. GPS trackers show how animals move. The sonar allows you to explore the oceans. And so on.
Undoubtedly, this is a vital mechanism, but there are at least two other paths from technology to knowledge. They may not be so simple, but I think they are just as important:
First . Technology leads to economic abundance (that is, wealth), and this allows more people to engage in the production of knowledge.
If 90% of your country's population is engaged in agriculture, and the remaining 10% are engaged in one form or another of trade (or war), then people have little free time to think about the laws of nature. Perhaps that is why, in earlier times, science was mainly promoted by children from rich families.
The United States annually produces more than 50,000 doctors of science. Instead of a person going to work at a factory at the age of 18 (or earlier), a graduate student has to finance up to 30 or maybe up to 40 years - and even then it is not clear whether his work will bring any real economic effect. But it is necessary that a person has reached the front lines in his discipline, especially in such difficult areas as physics or biology.
The fact is that in terms of systems, specialists are expensive. And the ultimate source of social wealth, which is funded by these specialists, is a new technology: plow subsidizes a feather.
Second. New technologies, especially in the field of travel and communications, are changing the structure of social networks in which knowledge is growing. In particular, it allows experts and specialists to interact more closely with each other.
Among the notable inventions here are the printing press, steamboats and railways (facilitating travel and / or sending mail over long distances), telephones, airplanes and the Internet. All of these technologies contribute to network density, especially within specialized communities (where almost all the growth of knowledge occurs). For example, the correspondence networks that have emerged among European scientists in the late Middle Ages, or how modern physicists use arXiv.
Ultimately, both of these paths are similar. Both increase the density of the network of specialists, which in turn leads to an increase in knowledge:
For many years I have been rather dismissive of higher education. A short stay in graduate school left an unpleasant taste in the mouth. But now, when I look back and think (to abstract from all personal problems), I must conclude that higher education is still extremely important.
Academic social networks (for example, research communities) are one of the most perfect and valuable structures created by our civilization. Nowhere have we accumulated a large concentration of specialists focused on knowledge production. Nowhere have people developed a greater ability to understand and criticize each other’s ideas. This is the beating heart of progress. It is in these networks that the fire of enlightenment burns the most.
But we cannot take progress for granted. If the crisis with irreproducibility of experiments and taught us something, it is that science can have systemic problems. This is a kind of network degradation.
Suppose we distinguish between two ways to do science: real science and careerism . Real science is a practice that reliably produces knowledge. She is motivated by curiosity and characterized by honesty (Feynman: “You see, I just need to understand the world”). Careerism, on the contrary, is motivated by professional ambitions and is characterized by playing politics and scientific labels. It may look and act like a science, but does not produce reliable knowledge.
(Yes, this is an exaggerated dichotomy. Just a mental experiment. Do not blame me).
The fact is that when careerists take a place in the real research community, they spoil the job. They seek to promote themselves, while the rest of the community is trying to get new knowledge and share it. Instead of striving for clarity, careerists complicate and confuse everything to sound more impressive. They are engaged in (as Harry Frankfurt would say) scientific nonsense. And, therefore, we could model them as dead nodes, immune to the honest exchange of information necessary for the growth of knowledge:
Perhaps the best model is the one in which careerist sites are not just immune to knowledge, but actively disseminate fake knowledge . Counterfeit knowledge may include insignificant results, the importance of which is artificially inflated, or truly false results that arise from manipulation or fabricated data.
Regardless of how we model them, careerists certainly can strangle our scientific communities.
This is similar to the nuclear chain reaction we urgently need - we need an explosion of knowledge - only in our enriched U-235 is too large an admixture of the non-reactive isotope U-238, which suppresses the chain reaction.
Of course, there is no clear distinction between careerists and real scientists. In each of us lies a bit of careerism. The question is how long the network will withstand before the spread of knowledge fades away.
Oh, you read to the end. Thank you for reading.
CC0 all rights are not reserved. You can use this work as you see fit :).
Or consider this article you are reading. You probably found it on a social network , downloaded it from a computer network and are currently deciphering the meaning with the help of your neural network .
But no matter how much I thought about networks over the years, until recently I did not understand the importance of simple diffusion .
')
This is our topic for today: how, how chaotic everything moves and spreads. Some examples to whet your appetite:
- Infectious diseases, moving from carrier to carrier within a population.
- Memes spreading on the graph of followers on social networks.
- Forest fire
- Ideas and practices that penetrate the culture.
- A cascade of neutrons in enriched uranium.
A brief note about the form.
Unlike all my previous works, this essay is interactive. The original article contains interactive examples with sliders and buttons that control objects on the screen - approx. lane]
So let's get started. The first task is to develop a visual dictionary for distribution across networks.
Simple model
I am sure that you all know the basis of networks, that is, nodes + edges. To explore diffusion, one need only mark some nodes as active . Or, as epidemiologists like to say, are infected :

This activation or infection spreads across the network from node to node according to the rules we develop below.
Real networks are usually much larger than this simple network of seven nodes. They are also much more confusing. But for simplicity, we will build a toy model here to study the lattice, that is, the lattice network.
(The fact that the grid lacks realism is compensated by the fact that it is easy to draw;)
Except where otherwise indicated, there are four neighbors in the network nodes, for example:

And you need to imagine that these grids stretch endlessly in all directions. In other words, we are not interested in behavior that occurs only at the edges of the network or in small populations.
Given that the grids are so ordered, you can simplify them to pixels. For example, these two images represent the same network:

In one of the behaviors, the active node always passes the infection to its (uninfected) neighbors. But it is boring. Much more interesting things happen when transmission is probabilistic .
SIR and SIS
In the SIR (Susceptible-Infected-Removed) model, the node can be in three states:
- Susceptible (susceptible)
- Infected
- Removed
Here's how interactive simulation works [in the original article, you can choose the transmission rate of infection from 0 to 1, see the process step by step or as a whole - approx. lane]:
- Nodes start as susceptible, with the exception of a few nodes that start as infected.
- At each time step, infected nodes get a chance to pass the infection to each of their susceptible neighbors with a probability equal to the speed of transmission.
- Infected nodes then go to the “deleted” state, that is, they are no longer able to infect others or infect themselves.
In the context of the disease, removal may mean that the person has died or that he has developed immunity to the pathogen. We say that they are “removed” from the simulation, because nothing happens to them anymore.
Depending on what we are trying to model, you may need another model other than SIR.
If we mimic the spread of measles or an outbreak of a forest fire, SIR fits perfectly. But suppose that we imitate the spread of a new cultural practice, such as meditation. At first, the node (person) is susceptible, because it has never done this before. Then, if he starts meditating (perhaps, having heard about it from a friend), we will model him as an infected one. But if he stops the practice, he will not die and will not fall out of the simulation, because in the future he can easily adopt this habit again. So he goes back to a receptive state.
This is the SIS (Susceptible – Infected – Susceptible) model . In the classical model, two parameters: the transfer rate and the recovery rate. However, in the simulations for this article, I decided to simplify by lowering the recovery rate parameter. Instead, the infected node automatically returns to a susceptible state at the next time step, unless it is infected by one of its neighbors. In addition, we allow a node infected in step n to infect itself in step n + 1 with a probability equal to the transmission rate.
Discussion
As you can see, this is very different from the SIR model.
Since the nodes are never removed, even a very small and limited lattice can sustain SIS infection for a long time. The infection simply jumps from node to node and returns.
Despite the differences, SIR and SIS are surprisingly interchangeable for our purposes. Therefore, for the rest of the article we will focus on SIS - mainly because it is more tenacious and, therefore, it is more interesting to work with it.
Critical level
By playing around with the SIR and SIS models, you might have noticed something about the longevity of the infection. At very low transmission rates, such as 10%, the infection tends to die out. While at higher values, such as 50%, the infection remains alive and captures most of the network. If the network were infinite, we could imagine that it continues and spreads forever.
Such unlimited diffusion has many names: “viral”, “nuclear” or (in the title of this article) critical .
It turns out that there is a specific turning point that separates subcritical networks (doomed to extinction) from supercritical networks (capable of infinite growth). This tipping point is called the critical threshold , and this is a fairly common feature of diffusion processes in conventional networks.
The exact value of the critical threshold varies between networks. What is common is the presence of such a value.
[In the interactive demonstration from the original article, you can try to manually feel the critical threshold of the network by changing the value of the transmission rate. It is somewhere between 22% and 23% - approx. trans.]
At 22% (and below), the infection eventually dies out. At 23% (and above), the initial infection sometimes dies out, but in most cases it can survive and spread long enough to ensure its eternal existence.
(By the way, there is a whole scientific direction dedicated to the search for these critical thresholds for different network topologies. For a quick acquaintance, I recommend quickly scrolling through the Wikipedia article on the threshold ).
In general, this is how it works: below the critical threshold, any final infection in the network is guaranteed (with probability 1) eventually dies out. But above the critical threshold there is a probability (p> 0) that the infection will last forever, and at the same time it will extend arbitrarily far from the original place.
However, note that the supercritical network does not guarantee that the infection will last forever. In fact, it often fades away, especially in the very early stages of modeling. Let's see how this happens.
Suppose we started with one infected node and four neighbors. In the first step of modeling, an infection has 5 independent chances for spreading (including the chance to “spread” on itself in the next step):

Now suppose the transfer rate is 50%. In this case, in the first step, we throw a coin five times. And if five eagles fall out, the infection will be destroyed. This happens in about 3% of cases - and this is only in the first step. An infection that has survived the first step has a certain (usually smaller) probability to die out in the second step, some (even less) probability to die out in the third step, and so on.
Thus, even when the network is supercritical - if the transmission rate is 99% - there is a chance that the infection will disappear.
But the important thing is that it will not always fade away. If you add up the probability of attenuation of all steps to infinity, the result is less than 1. In other words, with a non-zero probability, the infection will continue forever. That's what it means for a network to be supercritical.
SISa: spontaneous activation
Up to this point, all our simulations began with a small piece of pre-infected nodes in the center.
But what if to start from scratch? Then we simulate spontaneous activation — the process by which a susceptible node infects by chance (not from one of its neighbors).
This is called the SISa model . The letter “a” means “automatic.”
In the SISa simulation, a new parameter appears - the spontaneous activation rate, which changes the frequency of spontaneous infection (the transmission rate parameter that we saw earlier is also present).
What is needed for the infection to spread throughout the network?
Discussion
You may have noticed in the simulation that an increase in the rate of spontaneous activation does not change whether the infection captures the entire network or not. Only the transfer rate determines whether the network is subcritical or supercritical. And when the network is subcritical (the transmission rate is less than or equal to 22%), no infection can spread to the whole grid, no matter how often it starts.
It is like lighting a fire in a wet field. You can set some dry leaves on fire, but the flame will quickly go out because the rest of the landscape does not ignite enough (subcritical). While on a very dry field (supercritical), a single spark is enough to start a raging fire.
Such things are observed in the field of ideas and inventions. Often the world is not ready for an idea, and in this case it can be reinvented again and again, but it does not catch the masses. On the other hand, the world can be fully prepared for an invention (large hidden demand), and as soon as it is born, it is accepted by all. In the middle are ideas that are invented in several places and are distributed locally, but it is not enough for any particular version to cover the entire network at once. In this latter category, we find, for example, agriculture and writing, which were independently invented by different human civilizations about ten and three times, respectively.
Immunity
Suppose we make some nodes completely invulnerable, that is, immune to activation. It’s as if they were originally in a remote state, and the SIS (a) model runs on the remaining nodes.
The immunity slider controls the percentage of nodes removed. Try changing its value (while the model is running!) And see how it affects the state of the network, whether it will be supercritical or not.
Discussion
Changing the number of unresponsive nodes completely changes the picture, will the network be pre- or supercritical. And it is not difficult to understand why. With a large number of unresponsive sites, the infection has fewer opportunities to spread to new hosts.
It turns out that this entails a number of very important practical consequences.
One of them is to prevent the spread of forest fires. At the local level, each person must take his own precautions (for example, never leave an open flame unattended). But on a large scale, individual flashes are inevitable. Thus, another method of protection is to ensure a sufficient number of “gaps” (in a network of flammable materials) so that the flash does not cover the entire network. This function is performed by the glades:

Another outbreak that is important to stop is an infectious disease. The concept of population immunity is introduced here. This is the idea that some people cannot be vaccinated (for example, they have an impaired immune system), but if there are enough people susceptible to the infection, the disease cannot spread forever. In other words, a sufficient part of the population should be vaccinated in order to transfer the population from the supercritical to the subcritical state. When this happens, one patient can still become infected (for example, after a trip to another region), but without a supercritical network in which to grow, the disease will infect only a handful of people.
Finally, the concept of immune sites explains what happens in a nuclear reactor. In a chain reaction, a decaying uranium-235 atom releases about three neutrons, which cause (on average) the splitting of more than one U-235 atom. New neutrons then cause further splitting of atoms and so on exponentially:

When creating a bomb, the whole point is to ensure the smooth continuation of exponential growth. But at the power plant, the goal is to produce energy without killing everyone around. For this purpose, control rods made of a material capable of absorbing neutrons (for example, silver or boron) are used. Since they absorb, rather than release, neutrons, in our simulation they act as unresponsive nodes, thereby preventing the reactor core from going to a supercritical state.
Thus, the trick of a nuclear reactor is to keep the reaction near the critical threshold, moving the control rods back and forth, and ensure that whenever something goes wrong, the rods have fallen into the core and stopped it.
Power
The degree of a node is the number of its neighbors. Up to this point we have considered networks of the 4th degree. But what happens if you change this parameter?
For example, it is possible to connect each node not only with four direct neighbors, but also with four diagonally. In such a network the degree will be 8.
Gratings with degrees 4 and 8 are well symmetric. But with degree 5 (for example) the problem arises: which five neighbors to choose? In this case, we choose the four nearest neighbors (N, E, S, W), and then randomly select one neighbor from the set {NE, SE, SW, NW}. The choice is made independently for each node at each time step.
Discussion
Again, it is not difficult to understand what is happening here. When each node has more neighbors, the chances of spreading the infection increase — and thus the network is more likely to become critical.
However, the consequences may be unexpected, as we will see below.
Cities and network density
Until now, our networks have been completely homogeneous. Each node looks like any other. But what if we change the conditions and allow different states of nodes throughout the network?
For example, try to simulate the city. To do this, increase the density in some parts of the network (a higher degree of nodes). We do this on the basis of data that citizens have a wider social circle and more social interactions than people outside cities.
In our model, susceptible nodes are colored based on their degree. Nodes in the “countryside” have grade 4 (and are colored light gray), while nodes in the “cities” have higher degrees (and are painted darker), starting with grade 5 on the outskirts and ending at 8 in the city center .
Try to choose such a speed of propagation, so that the activation covers the cities, and then does not go beyond their borders.
I find this simulation both obvious and surprising. Of course , cities maintain a cultural level better than rural areas — everyone knows that. What surprises me is that part of this cultural diversity arises simply on the basis of the topology of the social network.
This is an interesting point, I will try to explain in more detail.
Here we are dealing with cultural forms that are transmitted simply and directly from person to person. For example, manners , salon games, fashion trends, linguistic trends, rituals of small groups and products that spread word of mouth, plus whole packets of information that we call ideas.
(Note: the dissemination of information between people is extremely complicated by the mass media. It is easier to imagine some technologically primitive environment, for example, Ancient Greece, where almost every spark of culture was transmitted by interaction in physical space).
From the above simulation, I learned that there are ideas and cultural practices that can take root and spread in the city, but they simply cannot spread in rural areas (mathematically they cannot). These are the same ideas and the same people. The point is not that the villagers have some kind of “near” ones: when interacting with the same idea, they have exactly the same chances to catch it as the citizens have. It’s just that the idea itself cannot become viral in rural areas, because there are not so many connections through which it can spread.
This is probably the easiest to see in the field of fashion - clothes, hairstyles, etc. In the network of fashion, we can fix the edge of the grid when two people notice each other's outfits. In the city center, every person can see more than 1,000 other people every day - on the street, in the subway, in a crowded restaurant, etc. In the countryside, on the contrary, each person can see only a couple of dozen others. Based only on this difference , the city is able to support more fashion trends. And only the most convincing trends - with the highest transmission speed - will be able to gain a foothold outside the city.
We tend to think that if the idea is good, then eventually it will reach everyone, and if the idea is bad, it will disappear. Of course, this is true in extreme cases, but between them there are a lot of ideas and practices that can become viral only in certain networks. This is really awesome.
Not only cities
We are here considering the effect of network density . It is defined for a given set of nodes as the number of actual edges divided by the number of potential edges . That is, the percentage of possible links that really exist.
So, we have seen that the density of the network in urban centers is higher than in rural areas. But cities are not the only place where we find dense networks.
An interesting example is secondary schools. For example, for a particular district, we compare the network that exists among schoolchildren with the network that exists among their parents. The same geographical area and the same population, but one network is many times denser than the other. It is therefore not surprising that fashion and linguistic tendencies spread much more quickly among adolescents.
Similarly, elite networks are usually much denser than non-elite networks — in my opinion, this fact is underestimated (people who are popular or influential spend more time creating networks, and therefore they have more “neighbors” than normal people). Based on the simulations above, we expect that elite networks will support some cultural forms that cannot be supported by the mainstream, simply on the basis of mathematical laws, by the average degree of the network. I leave you to reflect on what this may be for cultural forms.
Finally, we can apply this idea to the Internet, simulating it as a huge and very dense city. It is not surprising that many new types of culture flourish on the Internet, which are simply impossible to maintain in purely spatial networks: niche hobbies, better design standards, greater awareness of injustice, etc. And these are not only pleasant things. Just as the first cities were a breeding ground for diseases that could not spread with low population density, so the Internet is a breeding ground for malignant cultural forms, such as clickback, fake news, and incitement of artificial indignation.
Knowledge
“Attracting the right expert at the right moment is often the most valuable resource for creative problem solving.” - Michael Nielsen, “Inventing Discoveries”
We often think of discovery or invention as a process that occurs in the mind of a single genius. He is struck by a flash of inspiration and - eureka! - suddenly we get a new way to measure volume. Or the gravity equation. Or a light bulb.
But if we take the point of view of a lone inventor at the moment of discovery, then we look at the phenomenon from the point of view of a node . While it would be more correct to interpret the invention as a network phenomenon.
The network is important in at least two ways. First, already existing ideas must penetrate into the mind of the inventor. These are quotes from the new article, the bibliographic section of the new book - the giants, on whose shoulders Newton stood. Secondly, the network is crucial for bringing a new idea back into the world; an invention that has not spread can hardly be called an “invention” at all. Thus, for both these reasons, it makes sense to model the invention — or, in a broad sense, the growth of knowledge — as a process of diffusion.
In a moment, I will present a rough simulation of how knowledge within a network can spread and grow. But first I must explain.
At the beginning of the simulation, in each grid quadrant, there are four experts located as follows:
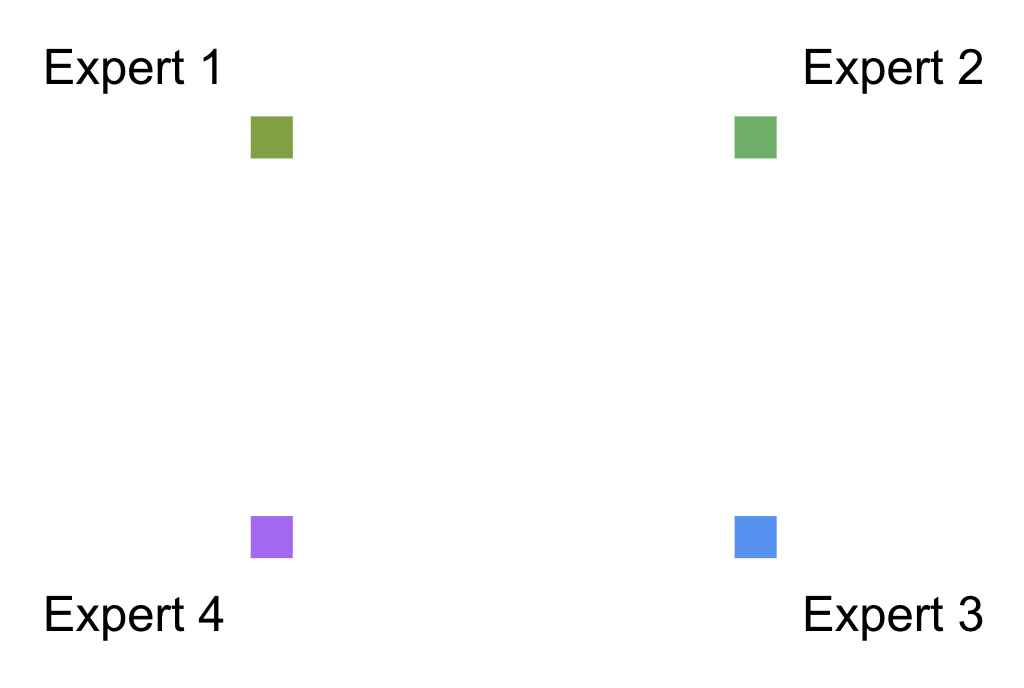
Expert 1 has the first version of the idea - let's call it Idea 1.0. Expert 2 is a person who knows how to turn Idea 1.0 into Idea 2.0. Expert 3 knows how to convert Idea 2.0 into Idea 3.0. And finally, the fourth expert knows how to make the final touches to create Idea 4.0.

This is like an origami technique, where methods are developed and combined with other methods to create more interesting designs. Or it may be a field of knowledge similar to physics, in which later work is based on the fundamental work of predecessors.
The essence of this simulation is that we need all four experts to contribute to the final version of the idea. And at each stage, the idea must be brought to the appropriate expert.
A few reservations. The simulation encoded many unrealistic assumptions. Here are just a few of them:
- It is assumed that ideas can not be saved and transmitted differently than from person to person (that is, there are no books and media).
- It is assumed that there are permanent experts in the population who are able to generate ideas, although in reality many random factors influence the emergence of discovery or invention.
- For all four versions of the idea, the same set of SIS parameters is used (transmission speed, percentage of immunity, etc.), although it is more realistic to use different parameters for each version (1.0, 2.0, etc.)
- It is assumed that the idea of N + 1 always completely crowds out the idea of N, although in practice often both the old and the new versions circulate at the same time, without a definitive winner.
… and many others.
Discussion
This is a ridiculously simplified model of how knowledge really grows. Outside the model there are a lot of important details (see above). Nevertheless, it reflects the important essence of the process. And therefore we can, with reservations, argue about the growth of knowledge, using our knowledge of diffusion.
In particular, the diffusion model provides an understanding of how to speed up the process : it is necessary to facilitate the exchange of ideas between expert nodes. This may mean clearing the network from dead nodes that prevent diffusion. Or it may mean the placement of all experts in a city or cluster with a large network density, where ideas quickly spread. Or just collect them in one room:
So ... that's all I can say about diffusion.
But I have one last thought, and it is very important. We are talking about the growth ( and stagnation ) of knowledge in scientific communities. This idea is different in tone and content from everything said above, but I hope you will forgive me.
About science networks
The illustration shows one of the most important positive feedback cycles in the world (and it was such a long time):

The upward cycle cycle (K ⟶ T) is quite simple: we use new knowledge to develop new tools. For example, understanding the physics of semiconductors allows us to create computers.
However, the downward movement requires some explanation. How does the development of technology lead to the growth of knowledge?
One of the ways - perhaps the most direct - is when new technologies give us new ways of perceiving the world. For example, the best microscopes allow you to take a deeper look inside the cell, throwing up ideas for molecular biology. GPS trackers show how animals move. The sonar allows you to explore the oceans. And so on.
Undoubtedly, this is a vital mechanism, but there are at least two other paths from technology to knowledge. They may not be so simple, but I think they are just as important:
First . Technology leads to economic abundance (that is, wealth), and this allows more people to engage in the production of knowledge.
If 90% of your country's population is engaged in agriculture, and the remaining 10% are engaged in one form or another of trade (or war), then people have little free time to think about the laws of nature. Perhaps that is why, in earlier times, science was mainly promoted by children from rich families.
The United States annually produces more than 50,000 doctors of science. Instead of a person going to work at a factory at the age of 18 (or earlier), a graduate student has to finance up to 30 or maybe up to 40 years - and even then it is not clear whether his work will bring any real economic effect. But it is necessary that a person has reached the front lines in his discipline, especially in such difficult areas as physics or biology.
The fact is that in terms of systems, specialists are expensive. And the ultimate source of social wealth, which is funded by these specialists, is a new technology: plow subsidizes a feather.
Second. New technologies, especially in the field of travel and communications, are changing the structure of social networks in which knowledge is growing. In particular, it allows experts and specialists to interact more closely with each other.
Among the notable inventions here are the printing press, steamboats and railways (facilitating travel and / or sending mail over long distances), telephones, airplanes and the Internet. All of these technologies contribute to network density, especially within specialized communities (where almost all the growth of knowledge occurs). For example, the correspondence networks that have emerged among European scientists in the late Middle Ages, or how modern physicists use arXiv.
Ultimately, both of these paths are similar. Both increase the density of the network of specialists, which in turn leads to an increase in knowledge:

For many years I have been rather dismissive of higher education. A short stay in graduate school left an unpleasant taste in the mouth. But now, when I look back and think (to abstract from all personal problems), I must conclude that higher education is still extremely important.
Academic social networks (for example, research communities) are one of the most perfect and valuable structures created by our civilization. Nowhere have we accumulated a large concentration of specialists focused on knowledge production. Nowhere have people developed a greater ability to understand and criticize each other’s ideas. This is the beating heart of progress. It is in these networks that the fire of enlightenment burns the most.
But we cannot take progress for granted. If the crisis with irreproducibility of experiments and taught us something, it is that science can have systemic problems. This is a kind of network degradation.
Suppose we distinguish between two ways to do science: real science and careerism . Real science is a practice that reliably produces knowledge. She is motivated by curiosity and characterized by honesty (Feynman: “You see, I just need to understand the world”). Careerism, on the contrary, is motivated by professional ambitions and is characterized by playing politics and scientific labels. It may look and act like a science, but does not produce reliable knowledge.
(Yes, this is an exaggerated dichotomy. Just a mental experiment. Do not blame me).
The fact is that when careerists take a place in the real research community, they spoil the job. They seek to promote themselves, while the rest of the community is trying to get new knowledge and share it. Instead of striving for clarity, careerists complicate and confuse everything to sound more impressive. They are engaged in (as Harry Frankfurt would say) scientific nonsense. And, therefore, we could model them as dead nodes, immune to the honest exchange of information necessary for the growth of knowledge:
Perhaps the best model is the one in which careerist sites are not just immune to knowledge, but actively disseminate fake knowledge . Counterfeit knowledge may include insignificant results, the importance of which is artificially inflated, or truly false results that arise from manipulation or fabricated data.
Regardless of how we model them, careerists certainly can strangle our scientific communities.
This is similar to the nuclear chain reaction we urgently need - we need an explosion of knowledge - only in our enriched U-235 is too large an admixture of the non-reactive isotope U-238, which suppresses the chain reaction.
Of course, there is no clear distinction between careerists and real scientists. In each of us lies a bit of careerism. The question is how long the network will withstand before the spread of knowledge fades away.
Oh, you read to the end. Thank you for reading.
License
CC0 all rights are not reserved. You can use this work as you see fit :).
Acknowledgments
- Kevin Kwok and Nicky Case for thoughtful comments and suggestions on various draft versions.
- Nicu Barra - for moral support throughout the process and for the most useful feedback on my work.
- Kitu A. for pointing out the phenomenon of percolation and percolation threshold.
- , ( ) .
- , « » ( ) « » . , .
- Distill.pub : .
- « » . , .
Source: https://habr.com/ru/post/452172/
All Articles