Bitmap indices in Go: search for wild speed

opening speech
I gave this talk in English at the conference GopherCon Russia 2019 in Moscow and in Russian at a meeting in Nizhny Novgorod. We are talking about a bitmap-index - less common than a B-tree, but no less interesting. I share the speech at the conference in English and text interpretation in Russian.
We will look at how a bitmap index works, when it is better, when it is worse than other indexes, and in which cases it is much faster than them; see in which popular DBMS already have bitmap-indices; try to write your own on Go. And “for dessert” we will use ready-made libraries to create our own super-fast specialized database.
')
I really hope that my works will be useful and interesting for you. Go!
Introduction
http://bit.ly/bitmapindexes
https://github.com/mkevac/gopherconrussia2019
Hello to all! It's six in the evening, we are all superb. Wonderful time to talk about the boring theory of database indexes, right? Do not worry, I will have a couple of lines of source code here and there. :-)
If without jokes, the report is full of information, but we do not have much time. So let's get started.

Today I will talk about the following:
- What are indexes;
- What is a bitmap-index;
- where it is used and where it is NOT used and why;
- simple implementation on Go and a bit of combat with the compiler;
- slightly less simple, but much more productive implementation on the Go-assembler;
- “Problems” of bitmap indexes;
- existing implementations.
So what are indexes?
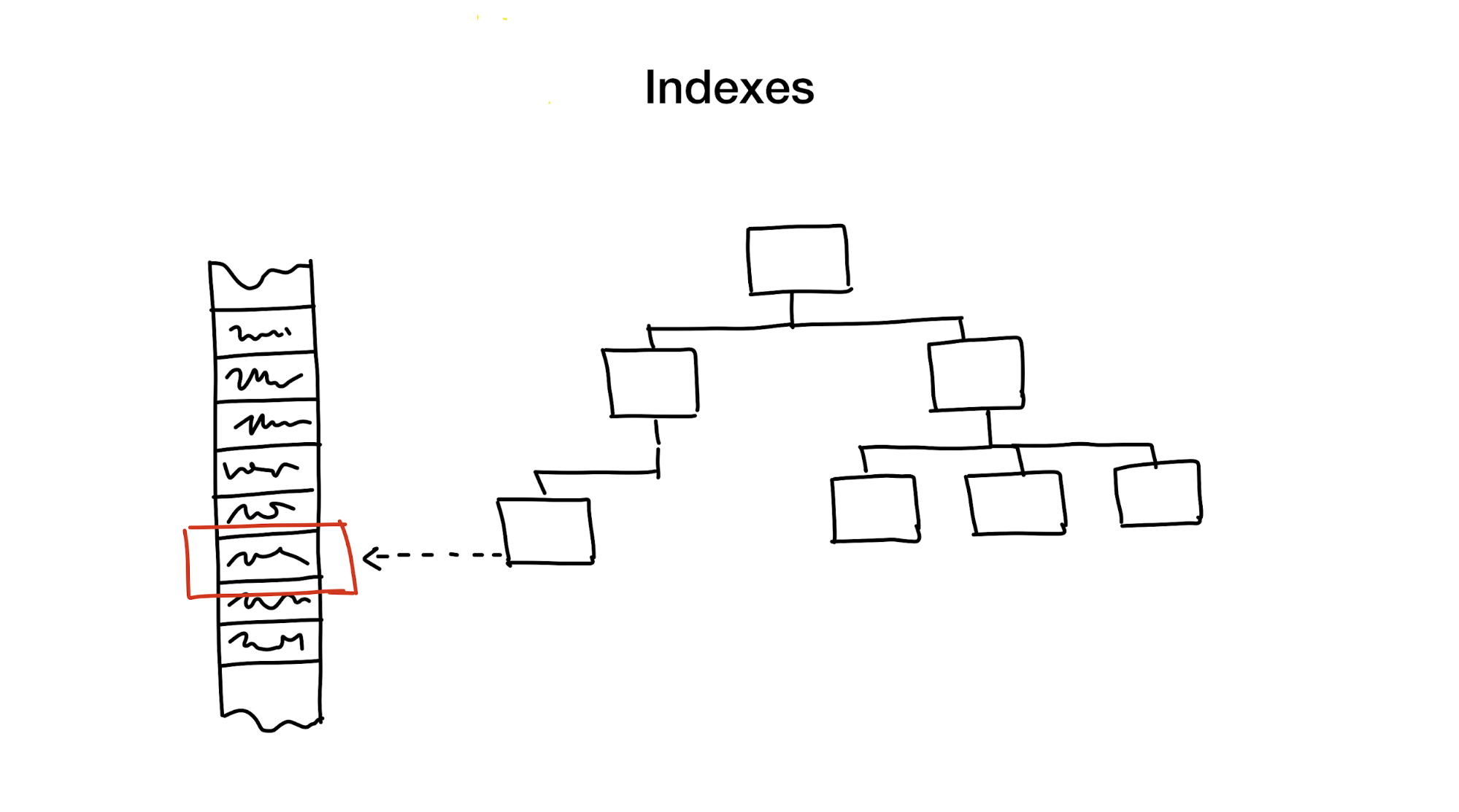
The index is a separate data structure that we keep and update in addition to the core data. It is used to speed up the search. Without indexes, a search would require a full pass through the data (a process called full scan), and this process has a linear algorithmic complexity. But databases usually contain a huge amount of data and linear complexity - this is too slow. Ideally, we would get logarithmic or constant.
This is a huge complex topic, full of subtleties and trade-offs, but, looking at decades of development and research of various databases, I am ready to assert that there are only a few widely used approaches to creating database indices.

The first approach is to hierarchically reduce the search area, dividing the search area into smaller parts.
We usually do this using different kinds of trees. An example would be a large box with the materials in your closet, in which there are smaller boxes with materials divided by various topics. If you need materials, then you will probably look for them in a box labeled "Materials", and not in the one that says "Cookies", right?
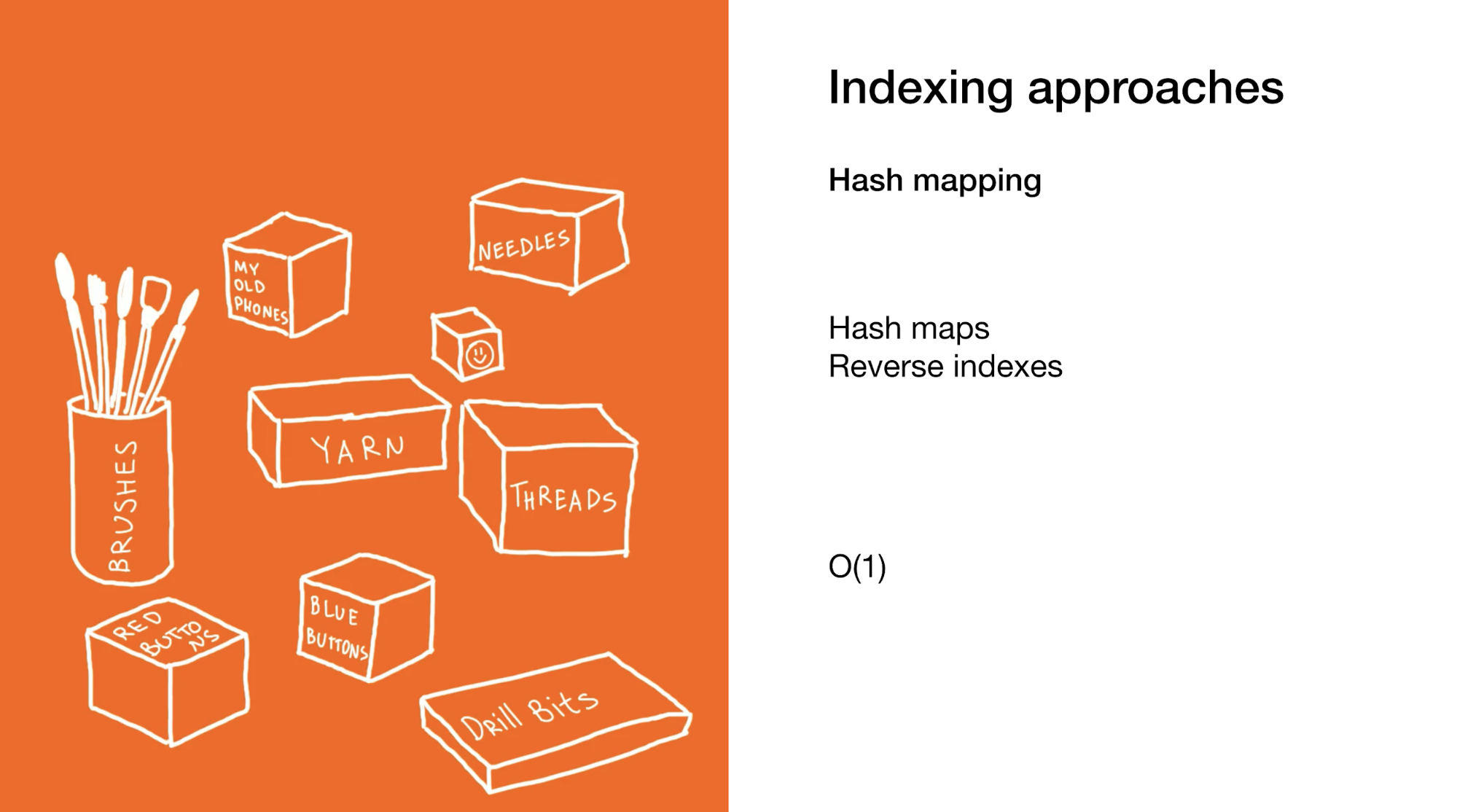
The second approach is to immediately select the desired element or group of elements. We do this in hash maps or in reverse indexes. Using hash maps is very similar to the previous example, only instead of a box with boxes in your closet a bunch of small boxes with final items.

The third approach is to get rid of the need to search. We do this using Bloom filters or cuckoo filters. The first give the answer instantly, saving you from having to search.
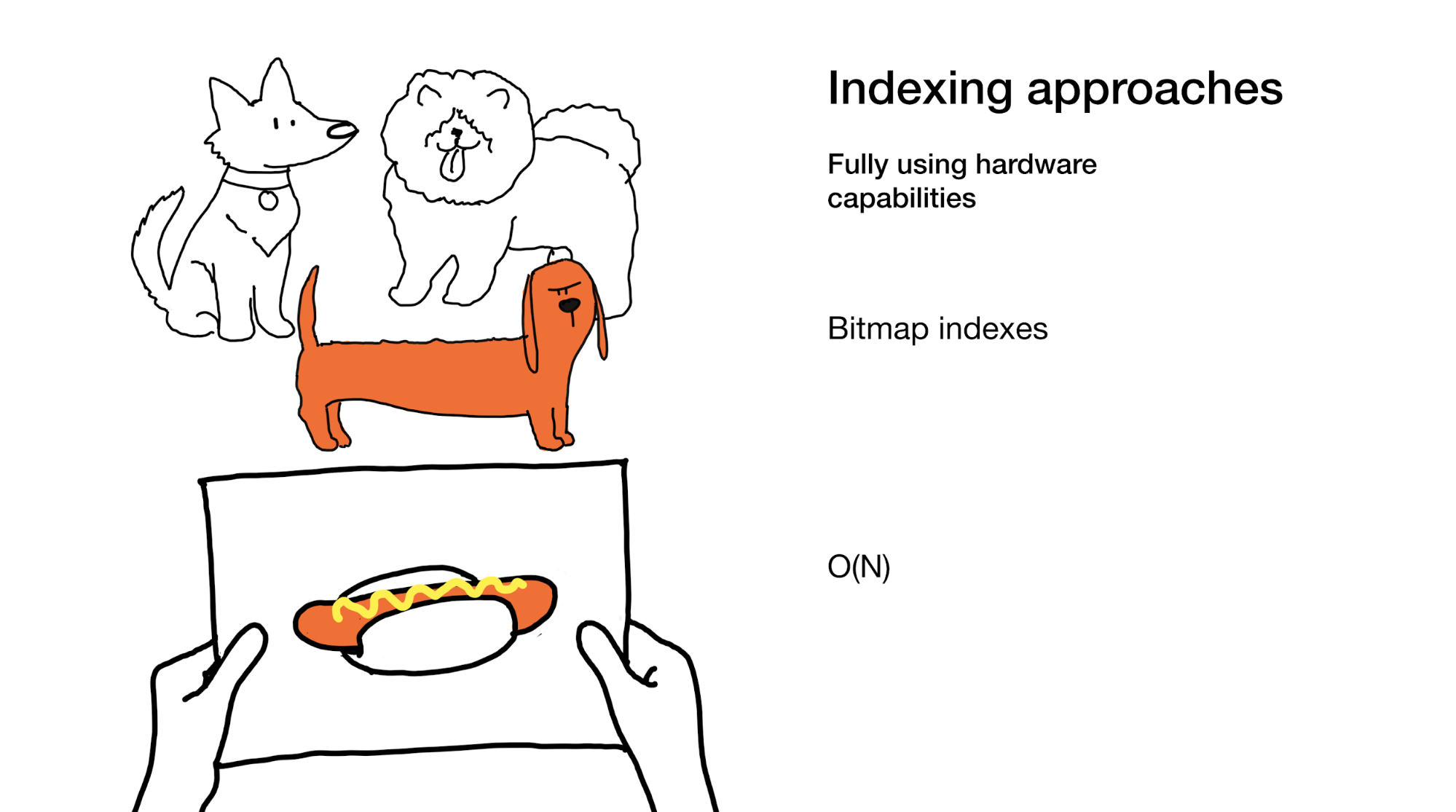
The latter approach is to fully utilize all the power that modern iron gives us. That is what we do in bitmap indexes. Yes, when using them, we sometimes need to go through the whole index, but we do it super-efficiently.
As I said, the topic of database indexes is extensive and full of compromises. This means that sometimes we can use several approaches at the same time: if we need to further accelerate the search or if it is necessary to cover all possible types of search.
Today I will talk about the least well-known approach of these - about bitmap-indices.
Who am I to talk about this topic?
I work as a team leader in Badoo (perhaps you know our other product better - Bumble). We already have more than 400 million users worldwide and many features that are committed to selecting the best pair for them. We do this with the help of custom services that use bitmap indexes as well.
So what is a bitmap index?
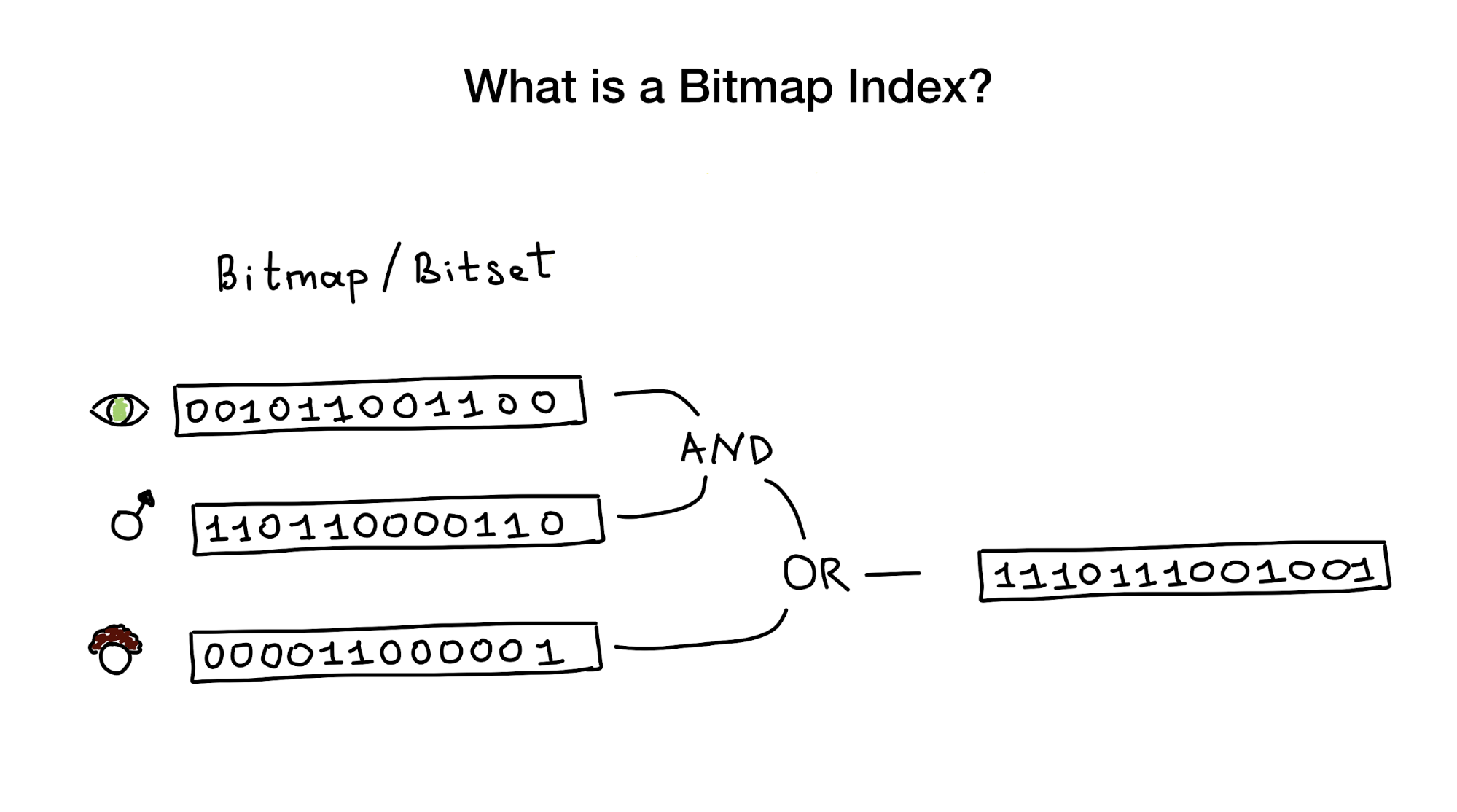
Bitmap indices, as the name suggests, use bitmaps or bitsets to embed a search index. From a bird's eye view, this index consists of one or more such bitmaps, representing any entities (such as people) and their properties or parameters (age, eye color, etc.), and from an algorithm using bit operations (AND, OR, NOT) to respond to a search query.

We are told that bitmap-indexes are best suited and very productive for cases where there is a search that combines queries on many columns that have little cardinality (imagine “eye color” or “marital status” against something like “distance from city center” ). But later I will show that they work fine in the case of columns with high cardinality.
Consider the simplest example of a bitmap index.

Imagine that we have a list of Moscow restaurants with binary properties like these:
- near the metro (near metro);
- there is a private parking (has private parking);
- there is a veranda (has terrace);
- can book a table (accepts reservations);
- suitable for vegetarians (vegan friendly);
- expensive
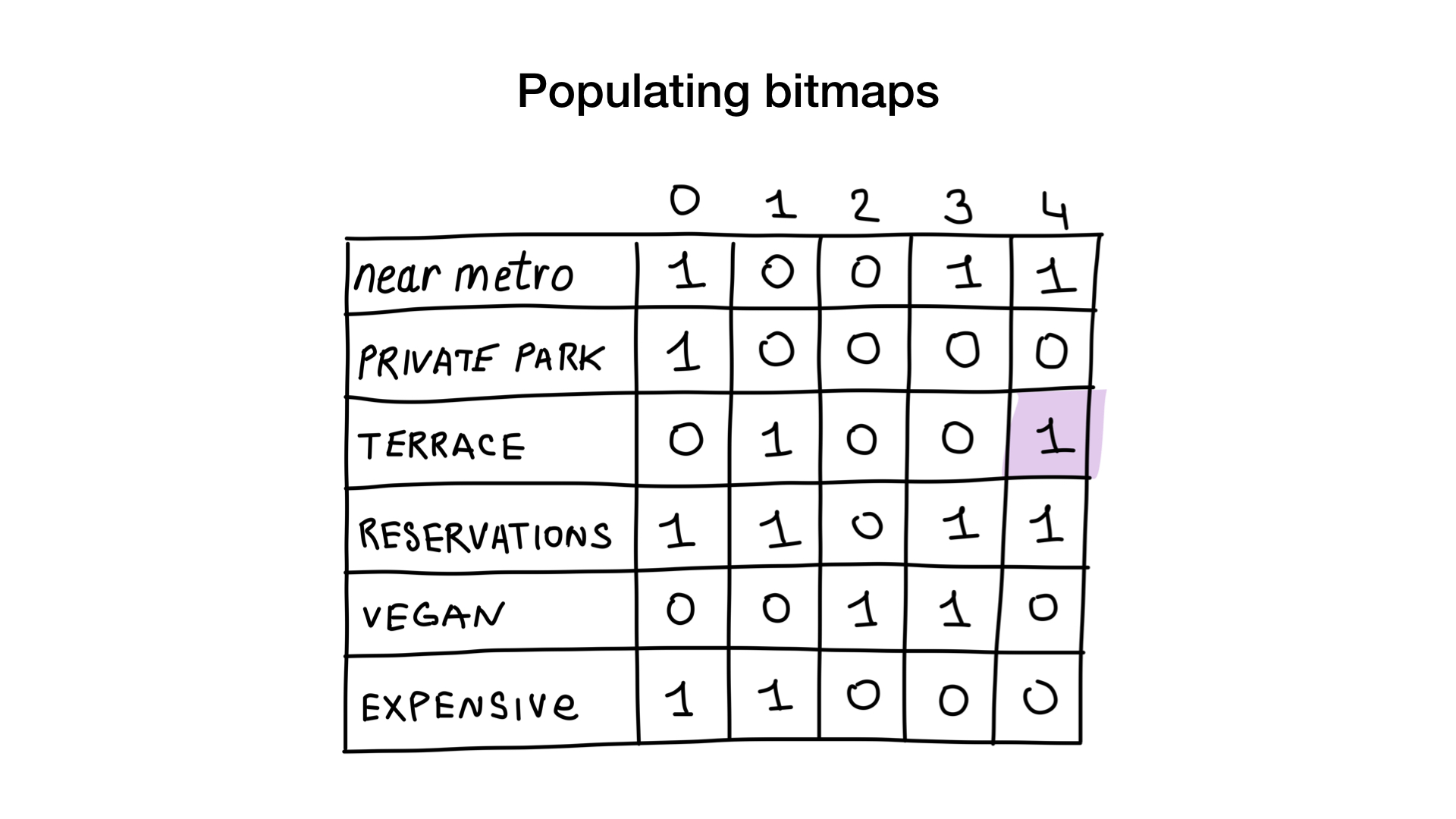
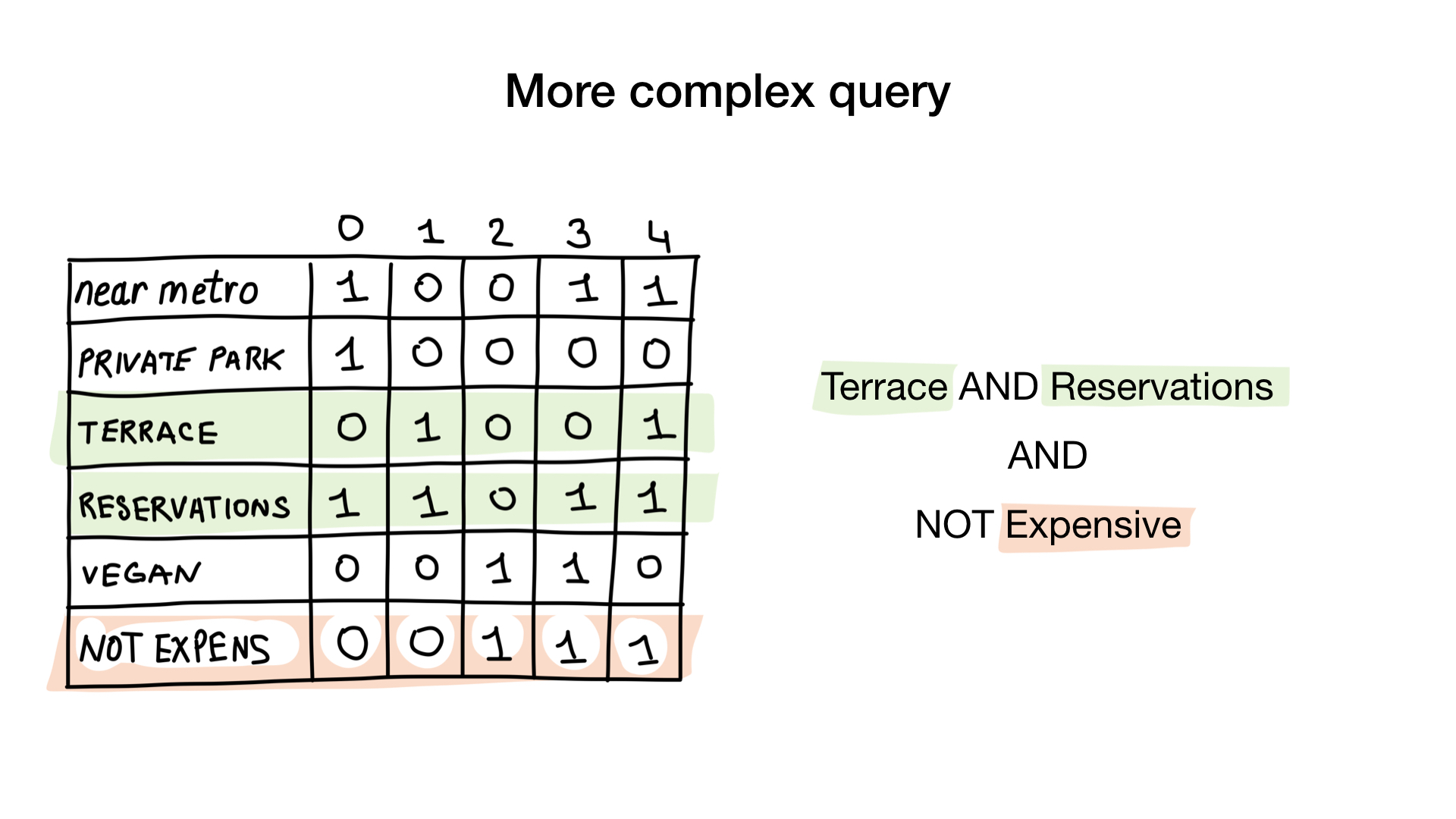
Let's give each restaurant a sequence number starting from 0 and allocate memory for 6 bitmaps (one for each characteristic). Then we fill in these bitmaps, depending on whether the restaurant has this property or not. If restaurant 4 has a veranda, then bit 4 in the bitmap “there is a veranda” will be set to 1 (if there is no veranda, then to 0).

Now we have the simplest bitmap index possible, and we can use it to answer queries like:
- "Show me restaurants suitable for vegetarians";
- "Show me cheap restaurants with a veranda where you can book a table."
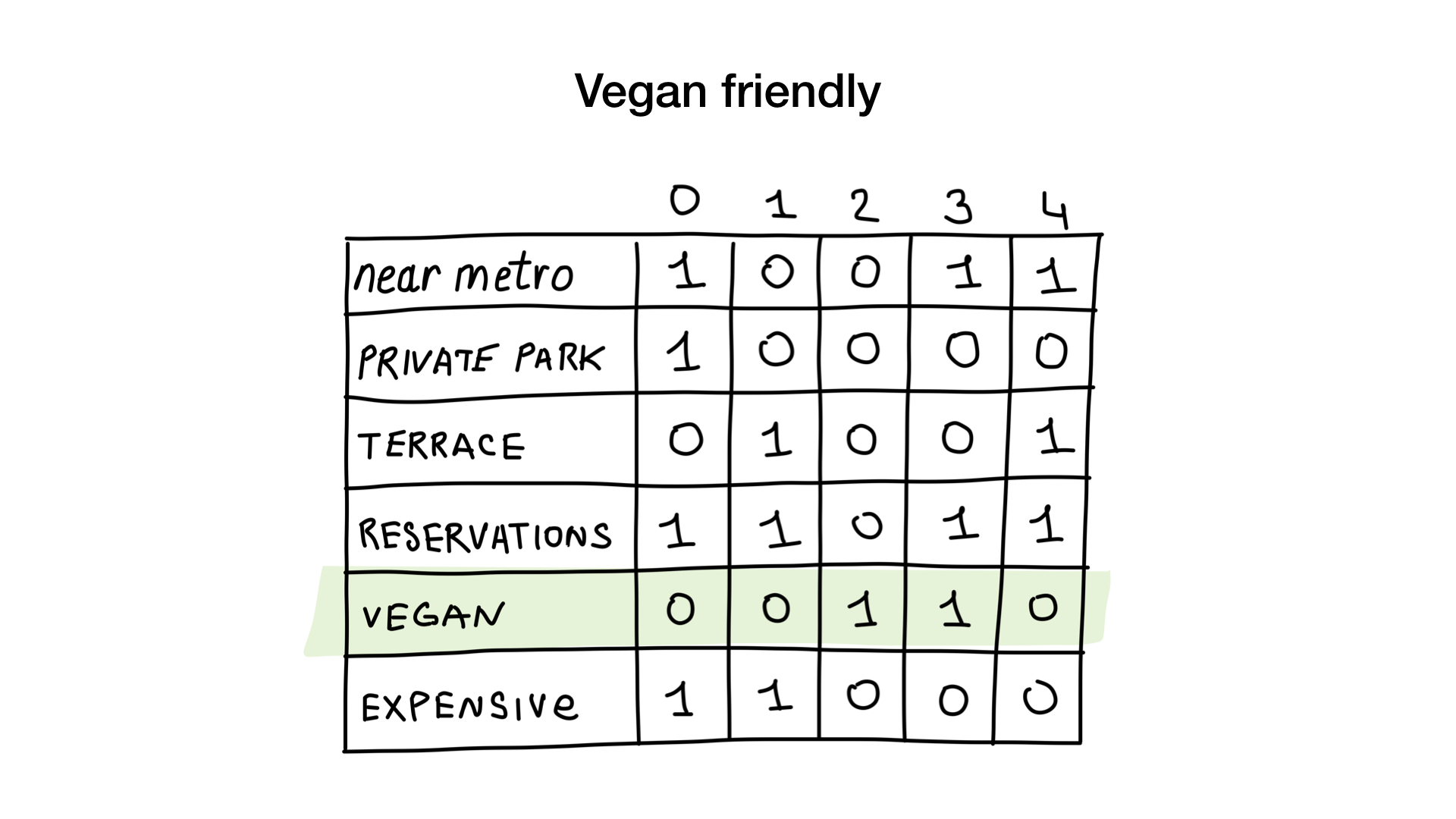
How? Let's get a look. The first request is very simple. All we need is to take a bitmap “suitable for vegetarians” and turn it into a list of restaurants whose bits are on display.
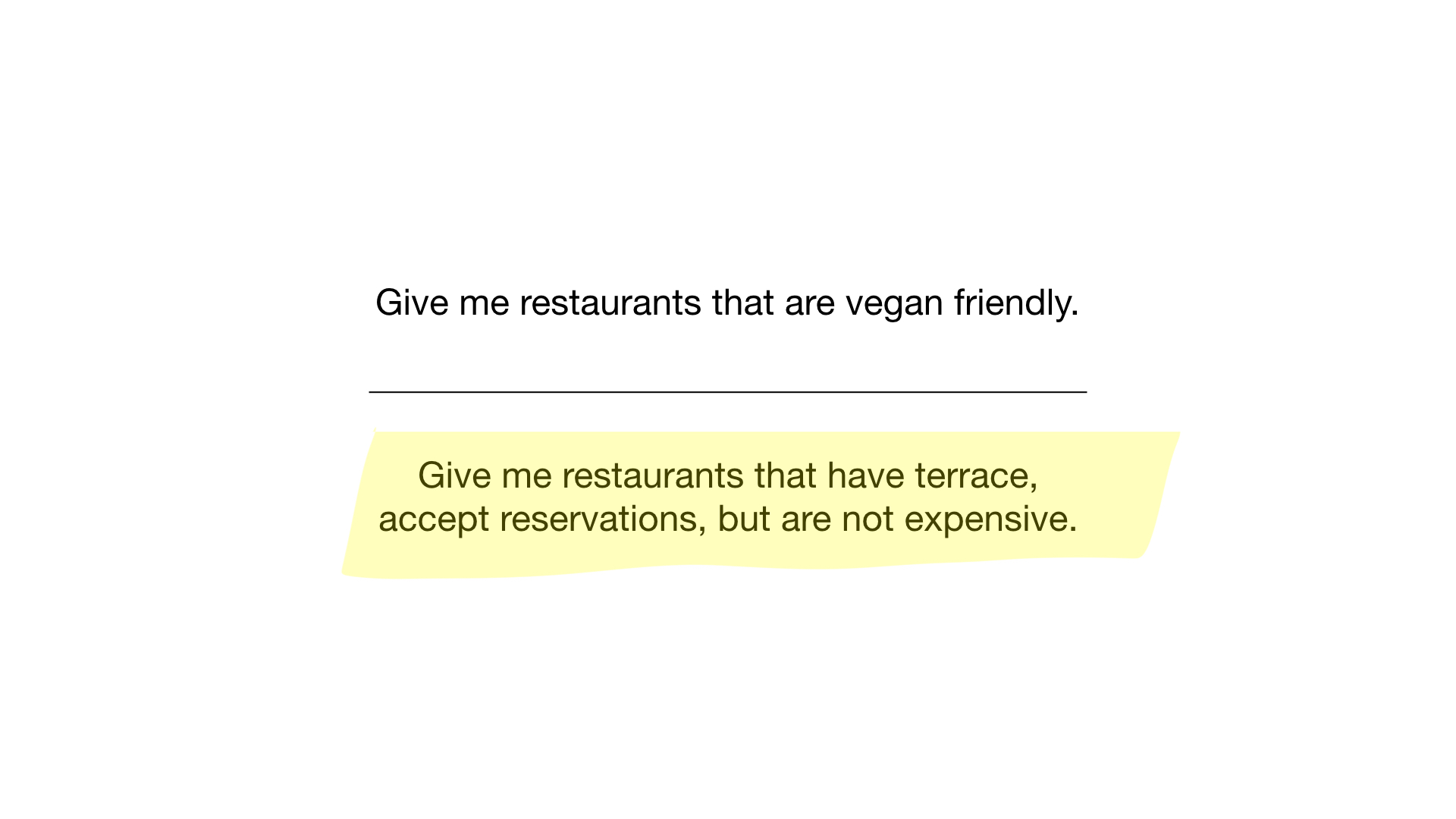

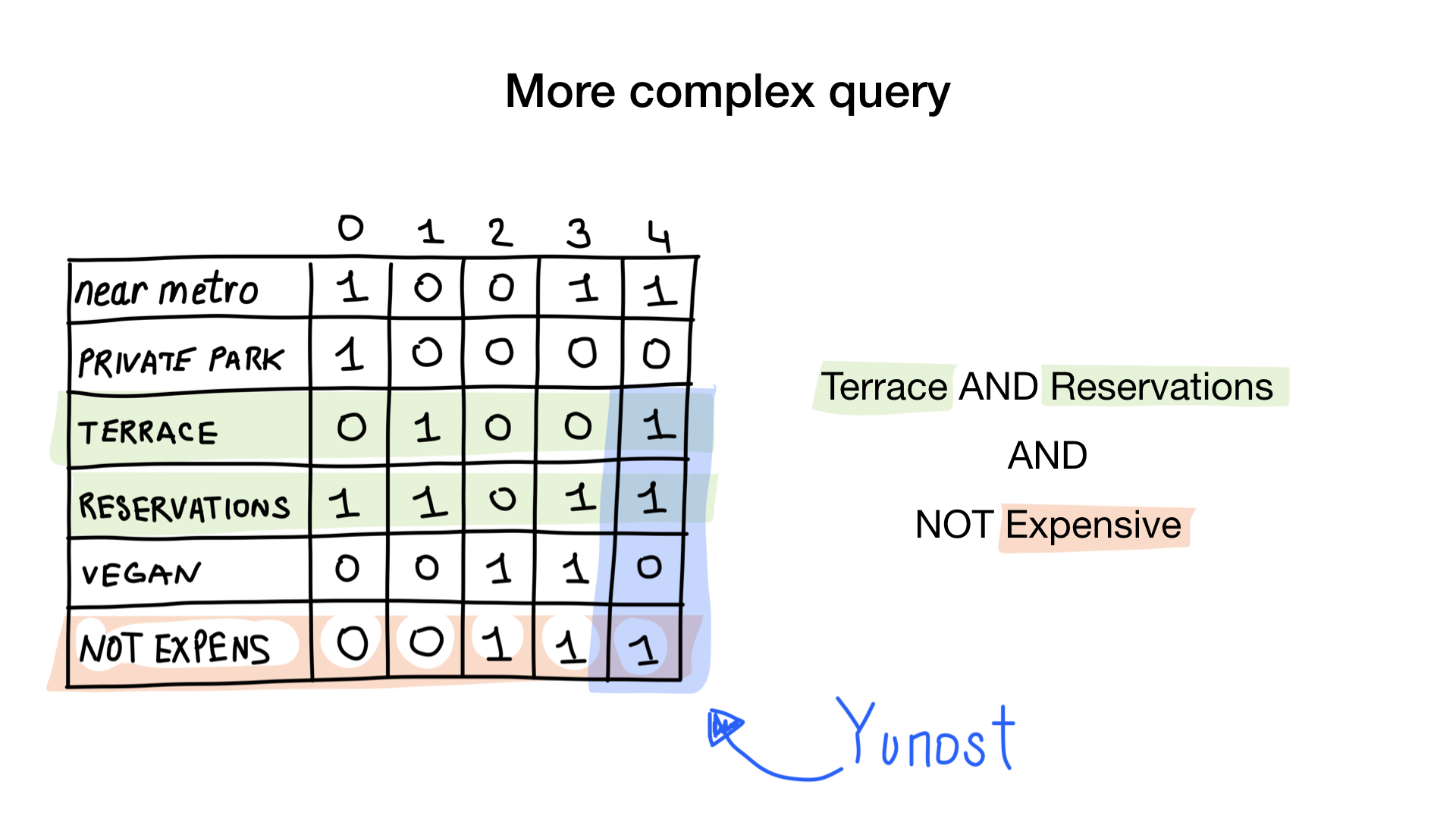
The second query is a bit more complicated. We need to use the NOT bit operation on the expensive bitmap in order to get a list of inexpensive restaurants, then for AND with it, you can book a table and for the result with a veranda bitmap. The resulting bitmap will contain a list of establishments that meet all our criteria. In this example, this is only the restaurant "Youth".
There is a lot of theory here, but don't worry, we will see the code very soon.
Where are bitmap indexes used?

If you google the bitmap indexes, 90% of the answers will be somehow connected to the Oracle DB. But the rest of the DBMS also supports such a cool thing too, right? Not really.
Let's go through the list of main suspects.

MySQL does not yet support bitmap indexes, but there is a Proposal with the suggestion to add this option ( https://dev.mysql.com/worklog/task/?id=1524 ).
PostgreSQL does not support bitmap indexes, but uses simple bitmaps and bit operations to combine search results for several other indexes.
Tarantool has bitset indexes, it supports a simple search for them.
Redis has simple bitfields (https://redis.io/commands/bitfield ) without the ability to search for them.
MongoDB does not yet support bitmap indexes, but there is also Proposal with the suggestion to add this option https://jira.mongodb.org/browse/SERVER-1723
Elasticsearch uses bitmaps inside (https://www.elastic.co/blog/frame-of-reference-and-roaring-bitmaps ).

- But in our house there was a new neighbor: Pilosa. This is a new non-relational database written in Go. It contains only bitmap indexes and bases everything on them. We will talk about her later.
Go implementation
But why are bitmap indexes so rarely used? Before answering this question, I would like to show you the implementation of a very simple bitmap index on Go.

Bitmaps are essentially just pieces of data. In Go, let's use byte slices for this.
We have one bitmap per restaurant characteristic, and each bit in bitmap tells us whether a particular restaurant has this property or not.

We need two auxiliary functions. One will be used to fill our bitmaps with random data. Randomized, but with a certain probability that the restaurant has every property. For example, I believe that in Moscow there are very few restaurants where a table cannot be booked, and it seems to me that about 20% of the establishments are suitable for vegetarians.
The second function will convert bitmap to a list of restaurants.


To answer the query “Show me cheap restaurants that have a veranda and where you can book a table,” we will need two bit operations: NOT and AND.
We can simplify our code a bit by using the more complex AND NOT operation.
We have functions for each of these operations. Both of them go in slices, take the corresponding elements from each, combine them with a bit operation and put the result in the resulting slice.
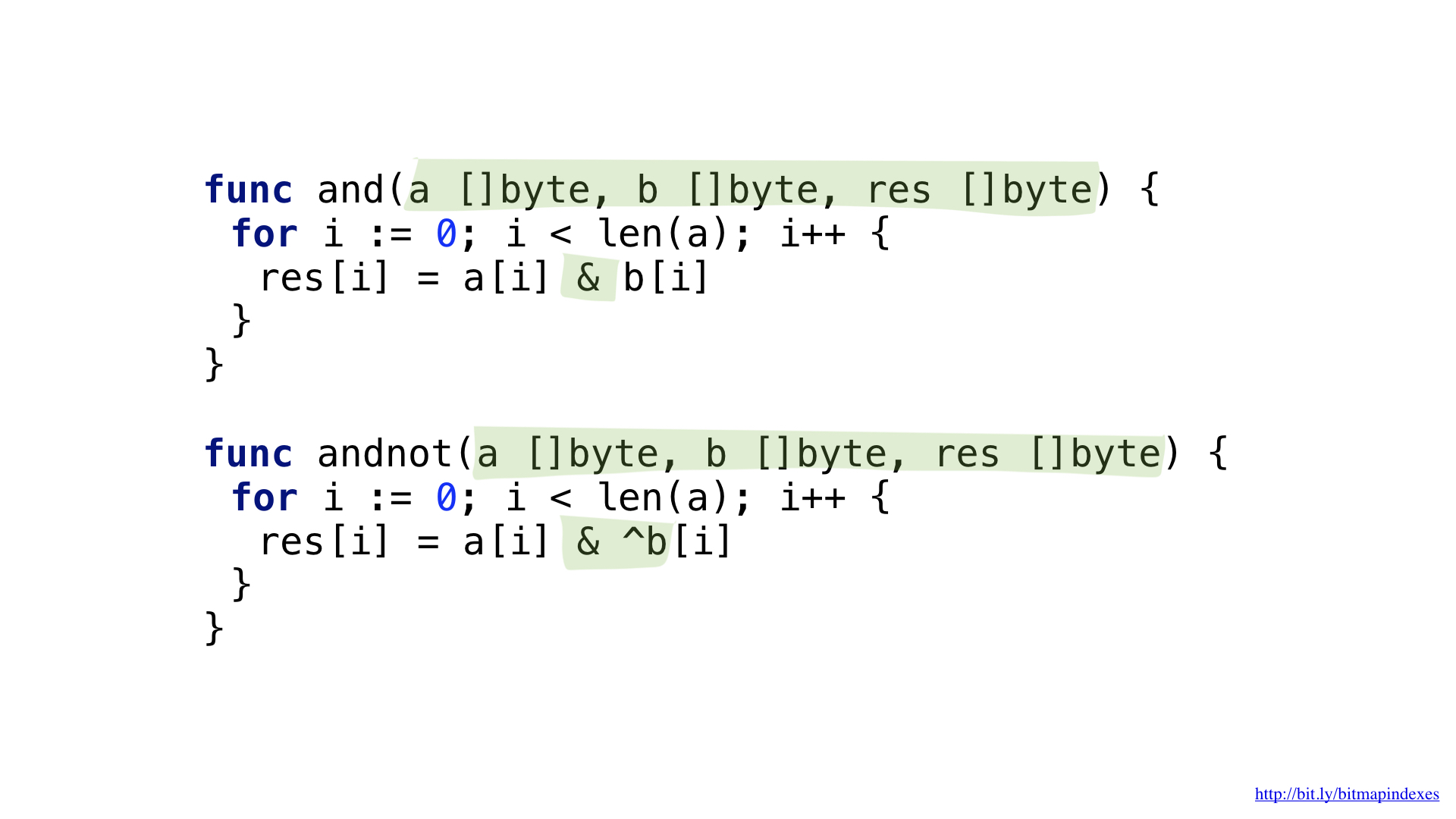
And now we can use our bitmaps and functions to respond to a search query.

The performance is not so high, even though the functions are very simple and we saved a lot by not returning a new result slice with each function call.
After profiling a bit with pprof, I noticed that the Go compiler missed one very simple, but very important optimization: function inlining.
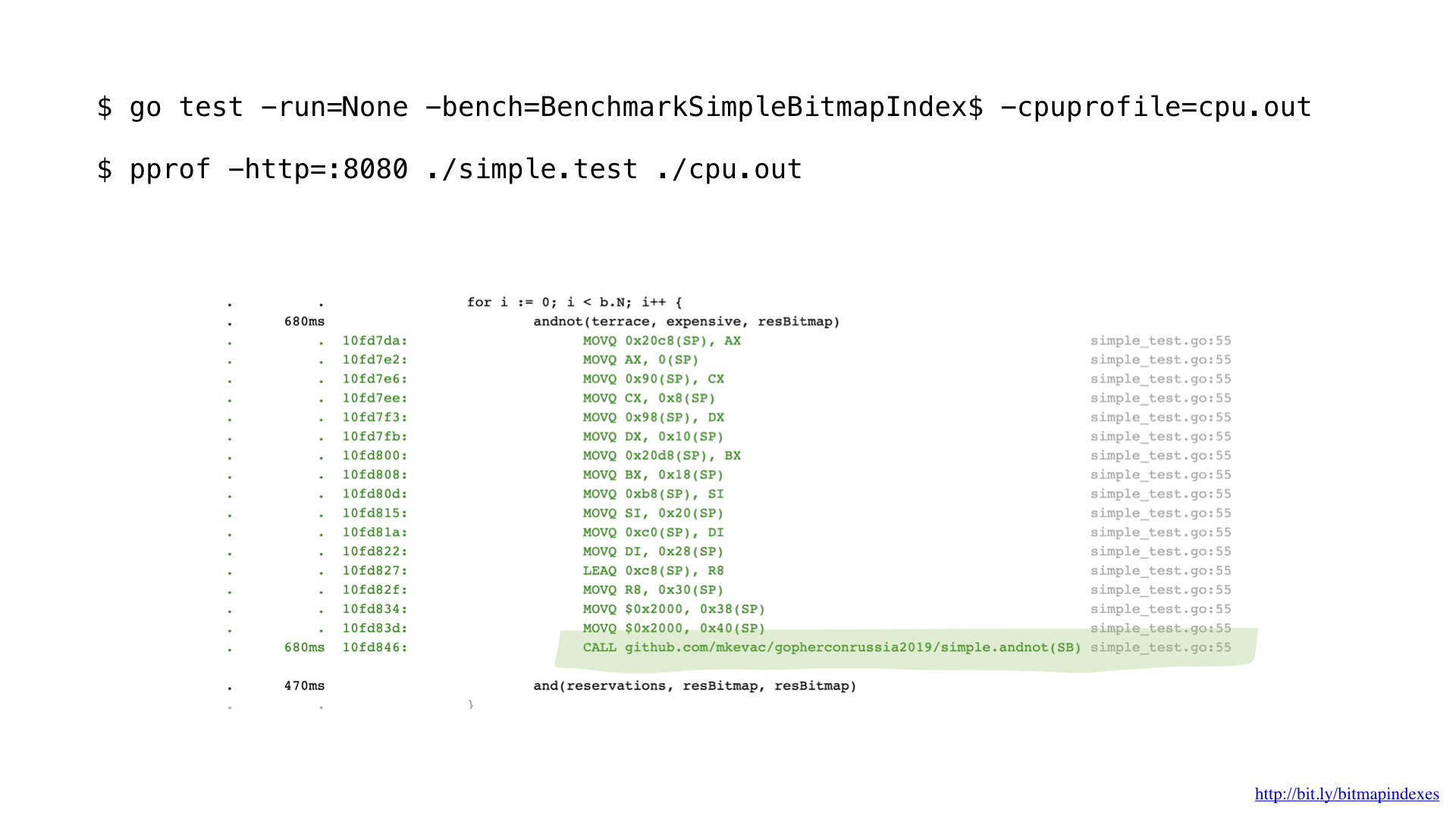
The fact is that the Go compiler is terribly afraid of the cycles that go along slices, and it categorically refuses to inline the functions that contain such cycles.
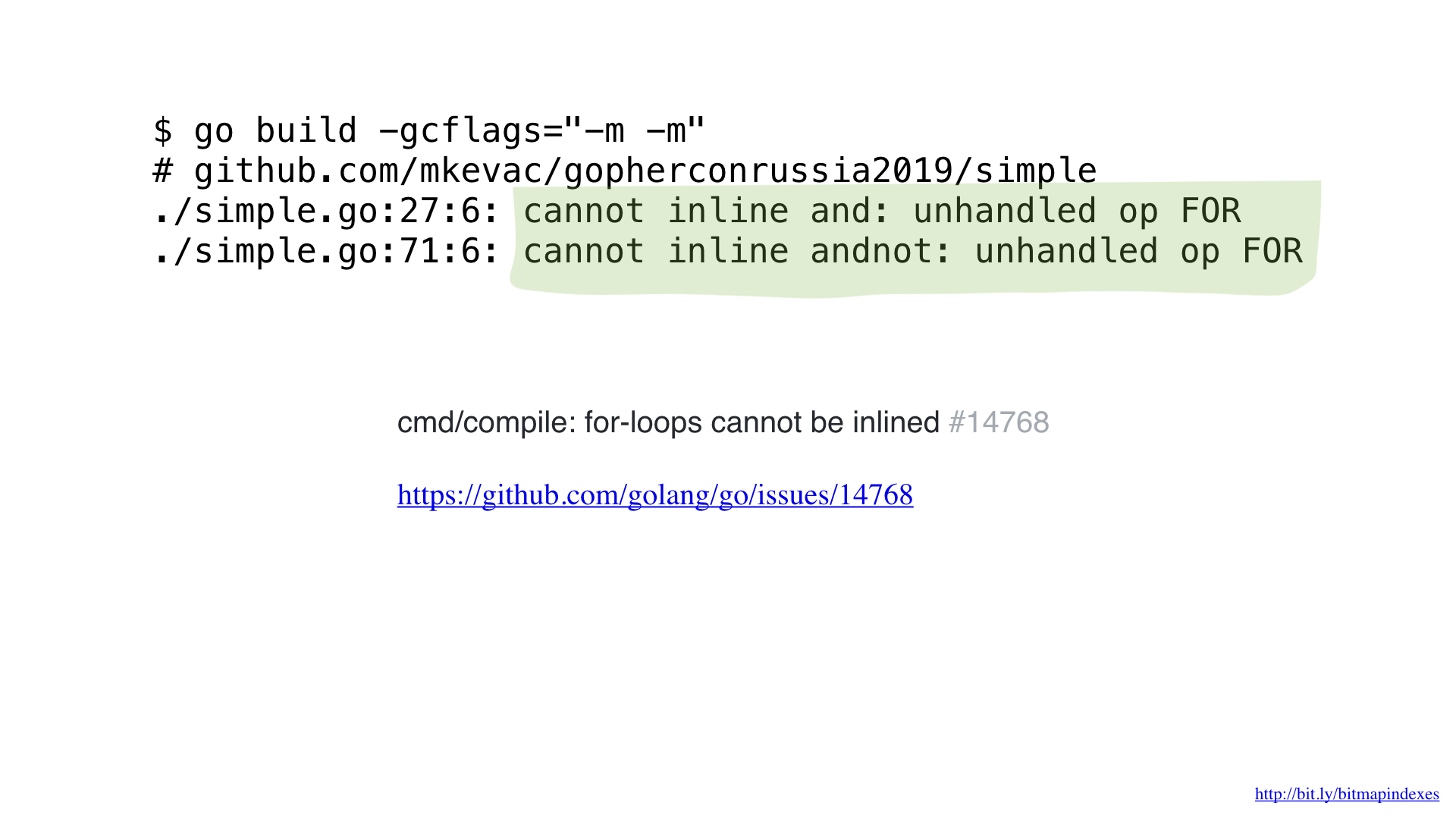
But I’m not afraid and I can fool the compiler by using goto instead of a loop, like in the good old days.


And, as you can see, now the compiler is happy to inline our function! As a result, we manage to save about 2 microseconds. Not bad!

The second bottleneck is easy to see if you look closely at the assembler output. The compiler added a check on the slice boundaries right inside our hottest loop. The fact is that Go is a safe language, the compiler fears that my three arguments (three slices) are of different sizes. After all, then there will be a theoretical possibility of the emergence of the so-called buffer overflow (buffer overflow).
Let's calm the compiler by showing him that all the slices have the same size. We can do this by adding a simple check at the beginning of our function.
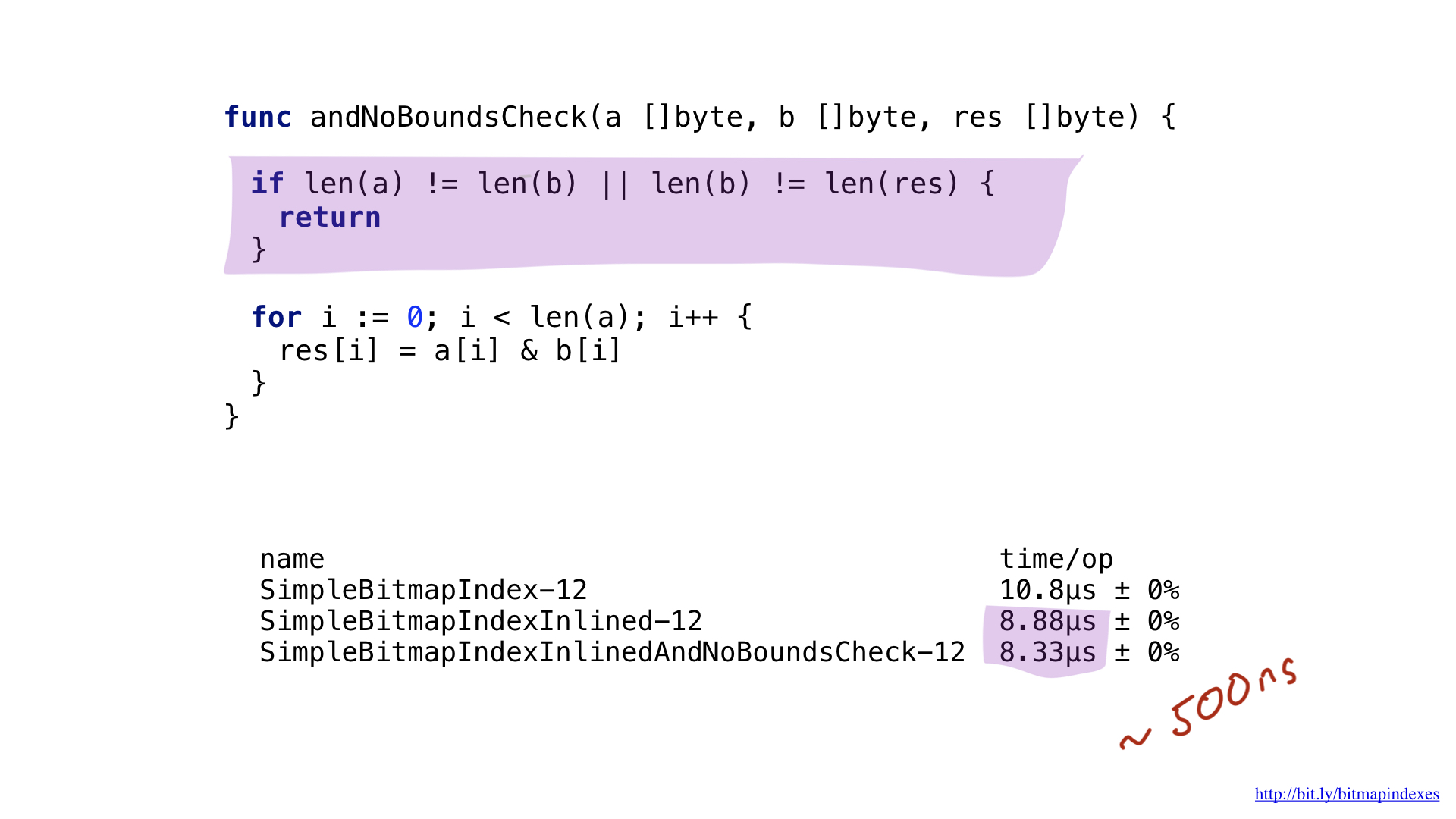
Seeing this, the compiler happily skips the check, and we end up saving another 500 nanoseconds.
Big batch
OK, we managed to squeeze out some performance from our simple implementation, but this result is, in fact, much worse than possible with the current hardware.
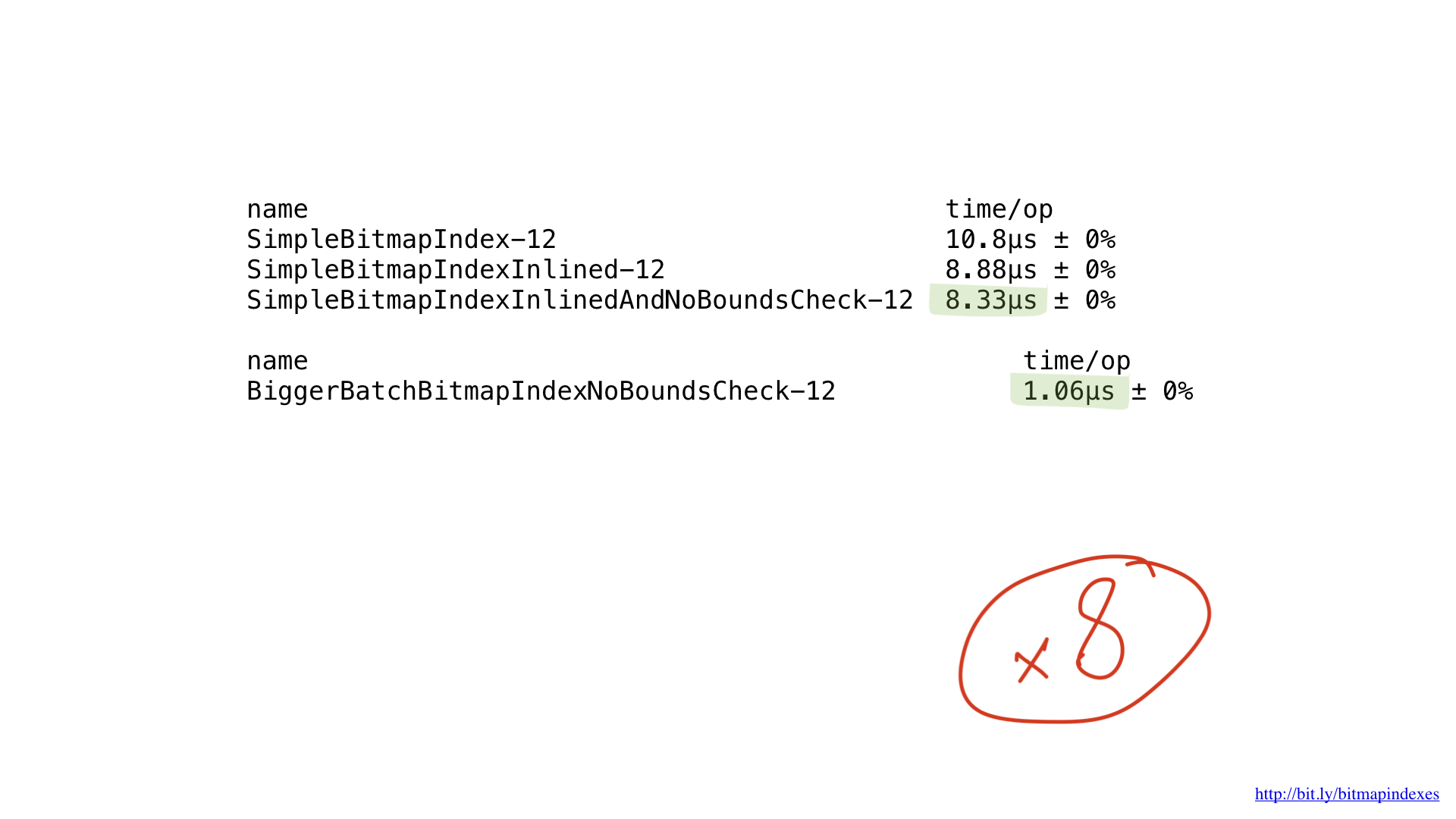
All that we do is basic bit operations, and our processors perform them very efficiently. But, unfortunately, we “feed” our processor with very small pieces of work. Our functions are performed by-byte operations. We can very easily tweak our code so that it works with 8-byte chunks using UInt64 slices.

As you can see, this small change accelerated our program eight times by increasing the batch eight times. The win can be said to be linear.
Implementation in assembly language

But this is not the end. Our processors can work with chunks of 16, 32 or even 64 bytes. Such “wide” operations are called single instruction multiple data (SIMD; one instruction, a lot of data), and the process of transforming the code so that it uses such operations is called vectorization.
Unfortunately, the Go compiler is far from excellent in vectorization. Currently, the only way to vectorize code on Go is to take and put these operations manually using Go assembler.

Assembler Go - a strange beast. You probably know that an assembler is something that is strongly tied to the architecture of the computer for which you are writing, but in Go it is not. Go assembler is more like IRL (intermediate representation language) or intermediate language: it is practically platform independent. Rob Pike gave an excellent talk on the subject a few years ago at GopherCon in Denver.
In addition, Go uses the unusual Plan 9 format, which is different from the generally accepted formats of AT & T and Intel.

It's safe to say that writing the assembler Go manually is not the most fun.
But, fortunately, there are already two high-level tools that help us in writing the Go assembler: PeachPy and avo. Both utilities generate Go-assembler from higher-level code written in Python and Go, respectively.

These utilities simplify things like register allocation (choosing a processor register), writing cycles, and generally simplify the process of entering the world of assembly programming in Go.
We will use avo, so our programs will be almost ordinary Go programs.

Here is the simplest example of the avo program. We have a main () function, which defines the Add () function inside itself, the meaning of which is the addition of two numbers. There are auxiliary functions for getting parameters by name and getting one of the free and suitable processor registers. Each processor operation has a corresponding function on avo, as seen by ADDQ. Finally, we see an auxiliary function for storing the resulting value.

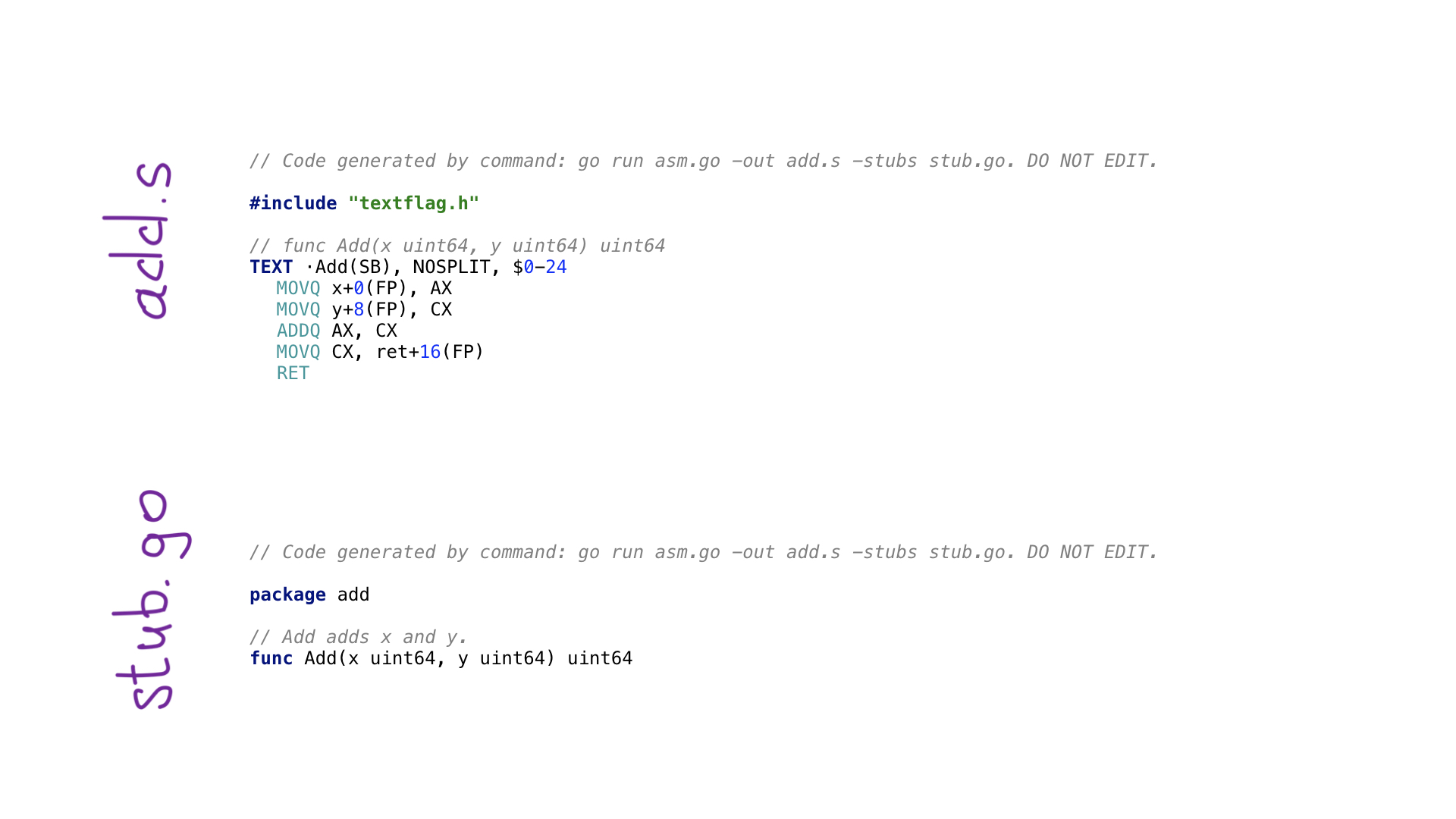
By calling go generate, we will execute the program on avo and as a result two files will be generated:
- add.s with the result code in Go-assembler;
- stub.go with headings of functions for communication of two worlds: Go and assembler.
Now that we have seen how and what makes avo, let's look at our functions. I implemented both scalar and vector (SIMD) versions of functions.
First, look at the scalar versions.

As in the previous example, we ask you to provide us with a free and correct general-purpose register; we do not need to calculate the offsets and sizes for the arguments. All this avo does for us.

Earlier we used labels and goto (or jumps) to improve performance and to trick the Go compiler, but now we do it from the very beginning. The fact is that cycles are a higher level concept. In assembly language, we only have labels and jumps.

The remaining code should be familiar and understandable. We emulate a cycle with labels and jumps, take a small part of the data from our two slices, combine them with a bit operation (AND NOT in this case) and then put the result into the resulting slice. Everything.

This is what the final assembly code looks like. We did not need to calculate the displacements and sizes (highlighted in green) or monitor the registers used (highlighted in red).
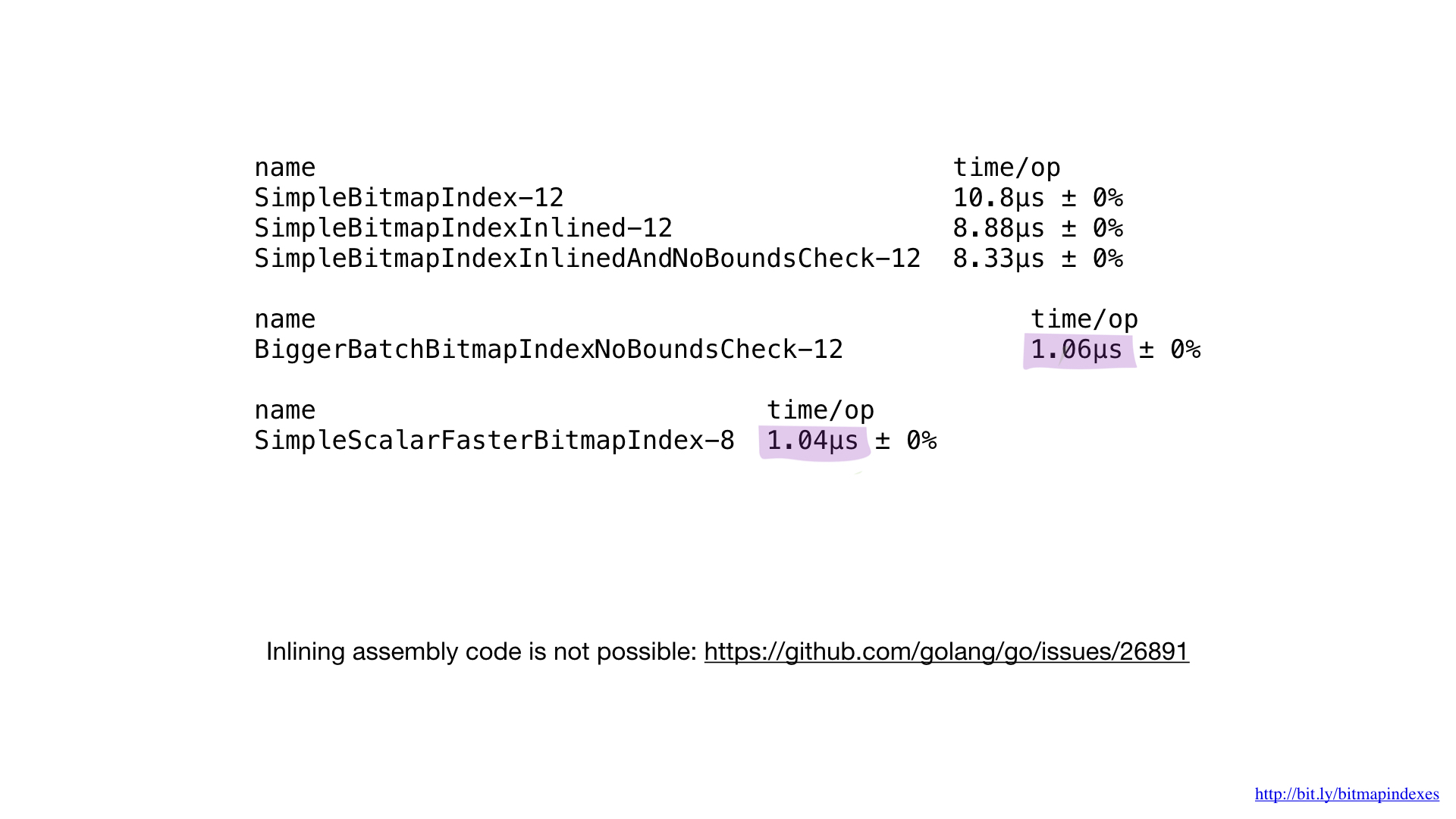
If we compare the performance of the implementation on the assembler with the performance of the best implementation on Go, then we will see that it is the same. And this is expected. After all, we did not do anything special - we just reproduced what the Go compiler would do.
Unfortunately, we cannot force the compiler to inline our functions written in assembler. The Go compiler doesn’t have such an opportunity today, although the request to add it has been around for quite a long time.
That is why it is impossible to get any benefits from small functions in assembler. We need to either write large functions, or use the new math / bits package, or bypass the assembler side.
Let's now look at the vector versions of our functions.

For this example, I decided to use AVX2, so we will use operations that work with 32-byte chunks. The structure of the code is very similar to the scalar version: loading parameters, please provide us with a free general register, etc.
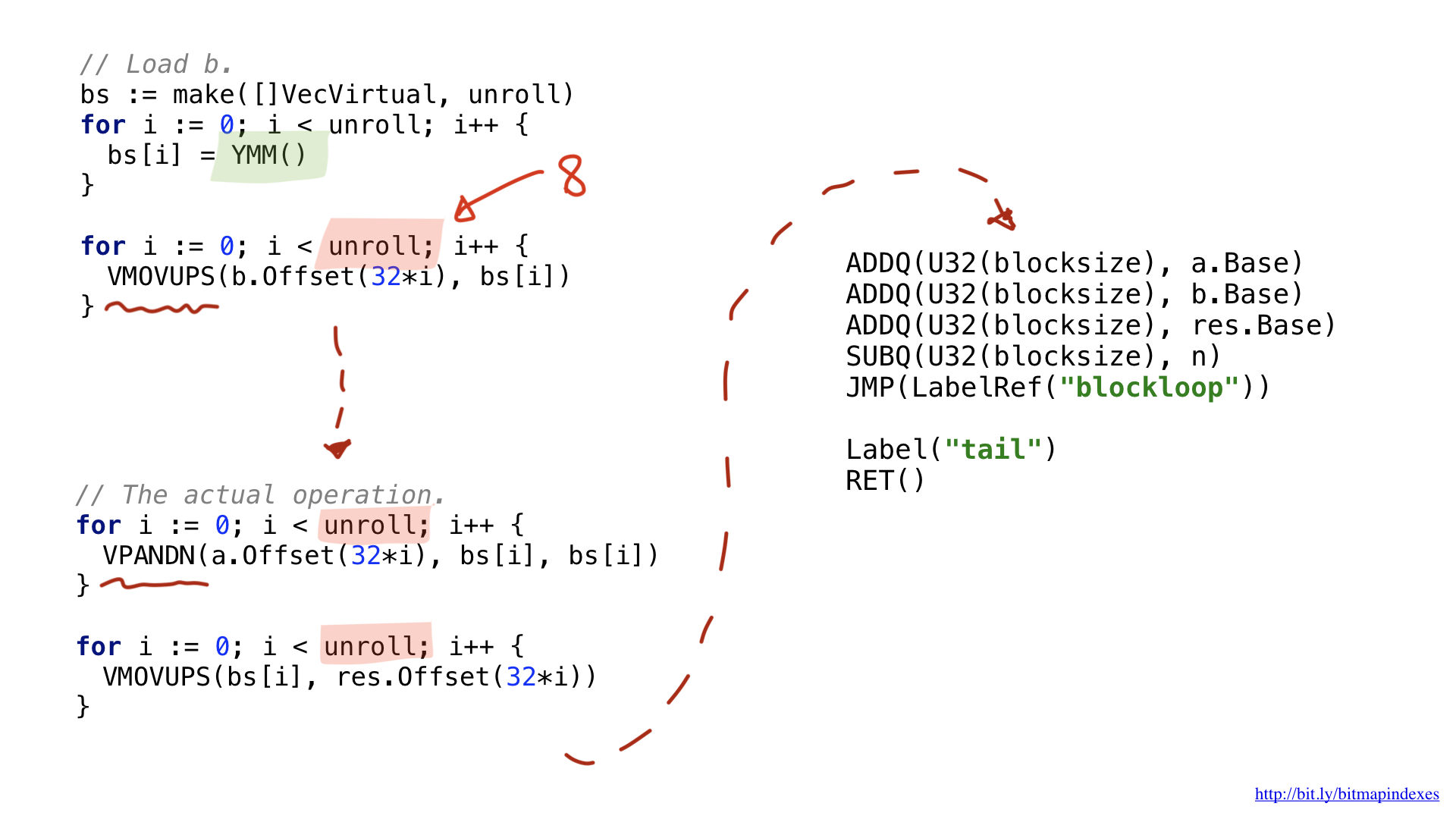
One of the innovations is due to the fact that wider vector operations use special wide registers. In the case of 32-byte chunks, these are registers with the Y prefix. That is why you see the YMM () function in the code. If I used the AVX-512 with 64-bit chunks, the prefix would be Z.
The second innovation is related to the fact that I decided to use an optimization called loop unrolling, that is, to do eight loop operations manually before jumping to the beginning of the loop. This optimization reduces the number of brunches (branches) in the code, and it is limited by the number of free registers available.
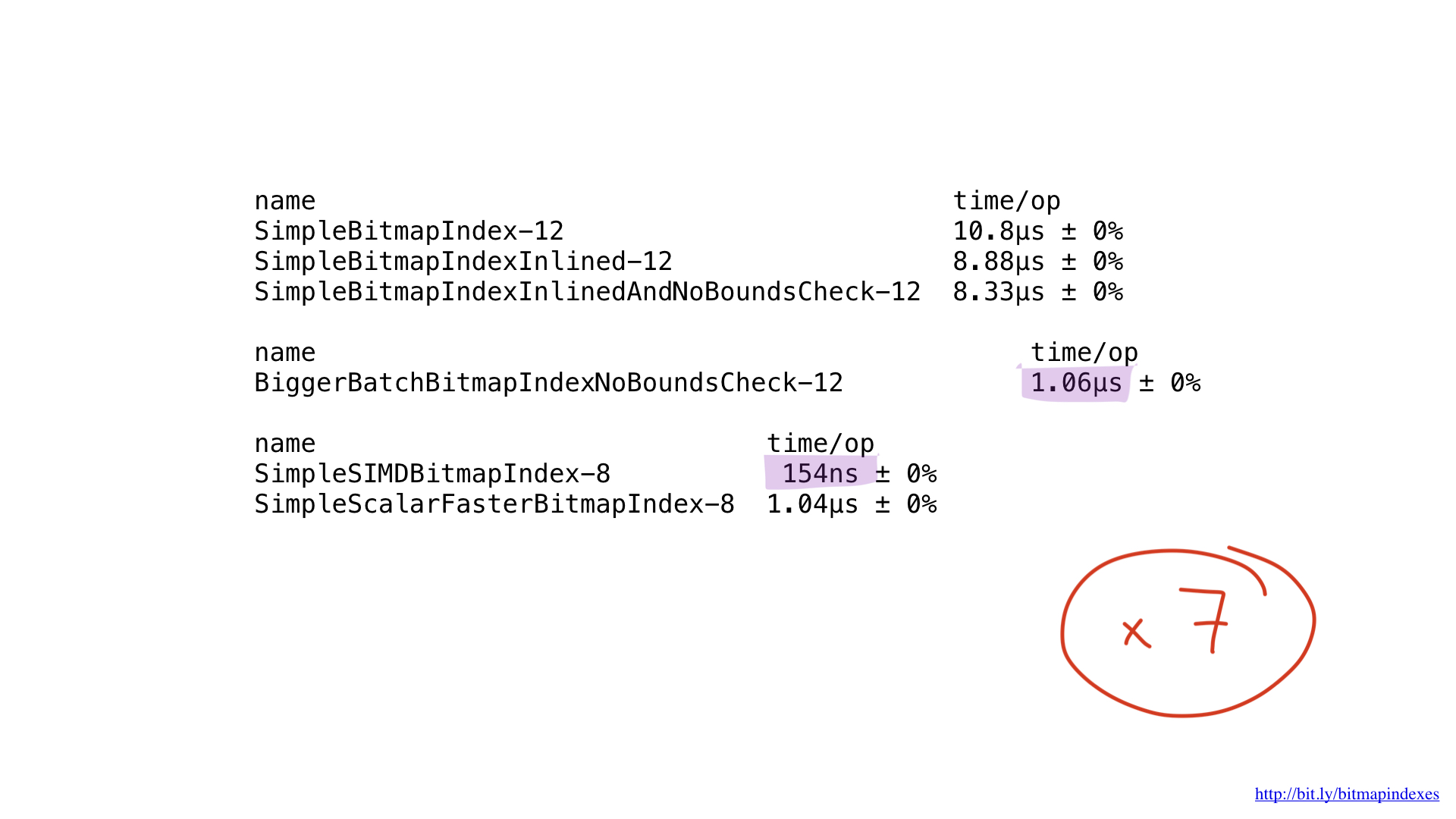
Well, what about performance? She is beautiful! We got about seven times faster than the best Go solution. Impressive, yes?
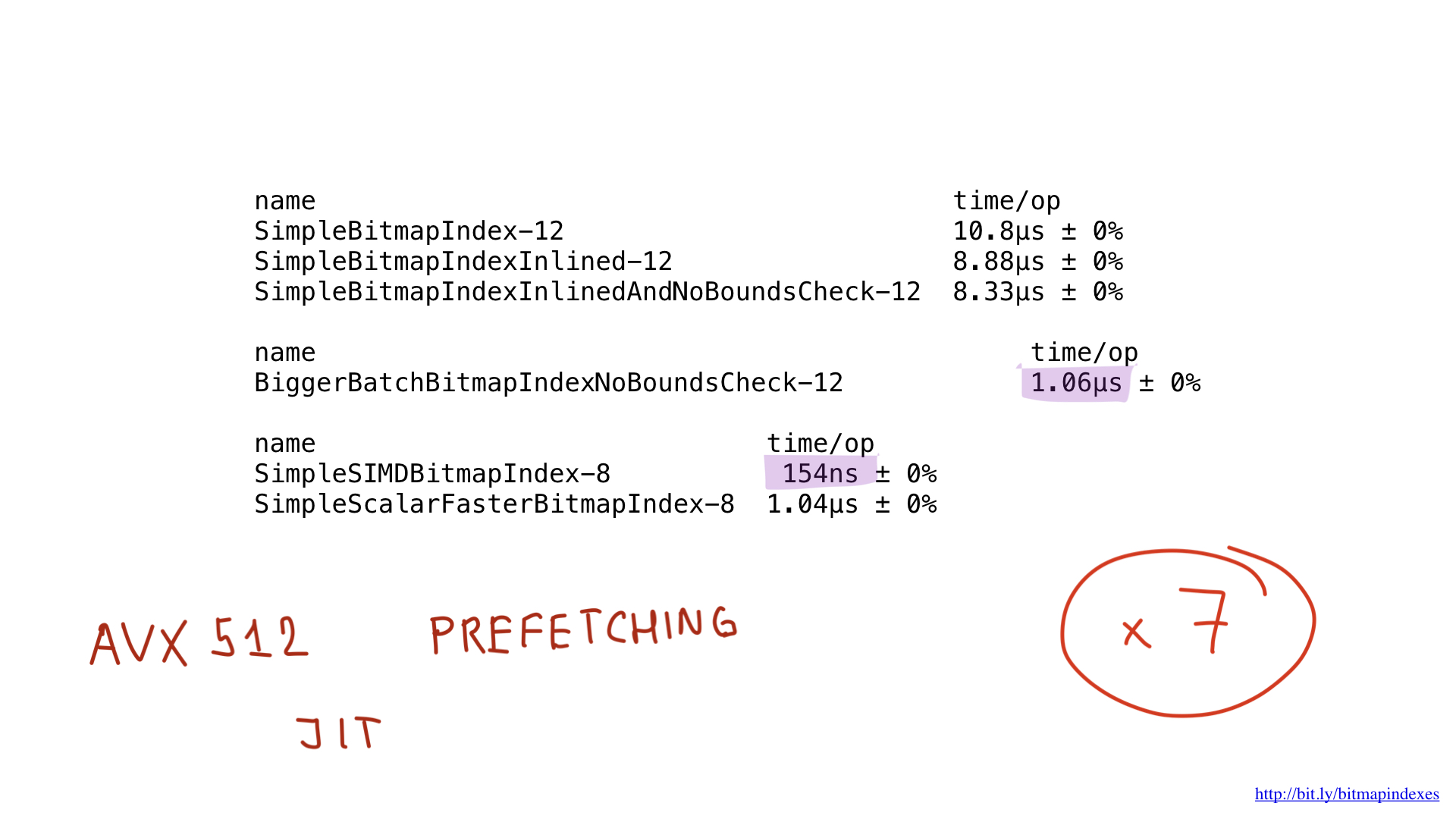
But even this implementation could potentially be accelerated using AVX-512, prefetching or JIT (just-in-time compiler) for the query planner. But this is certainly a topic for a separate report.
Bitmap Index Problems
Now, when we have already considered a simple implementation of a bitmap index on Go and much more productive on an assembler, let's finally talk about why bitmap indexes are so rarely used.

Older scientific papers mention three problems of bitmap-indices, but newer scientific papers and I state that they are already irrelevant. We will not dive deep into each of these problems, but we shall examine them superficially.
The problem of great cardinality
So, we are told that bitmap-indices are suitable only for fields with low cardinality, that is, those that have few values (for example, gender or eye color), and the reason is that the usual representation of such fields (one bit per value) in the case of large cardinality will take up too much space and, moreover, these bitmap-indices will be weakly (rarely) filled.
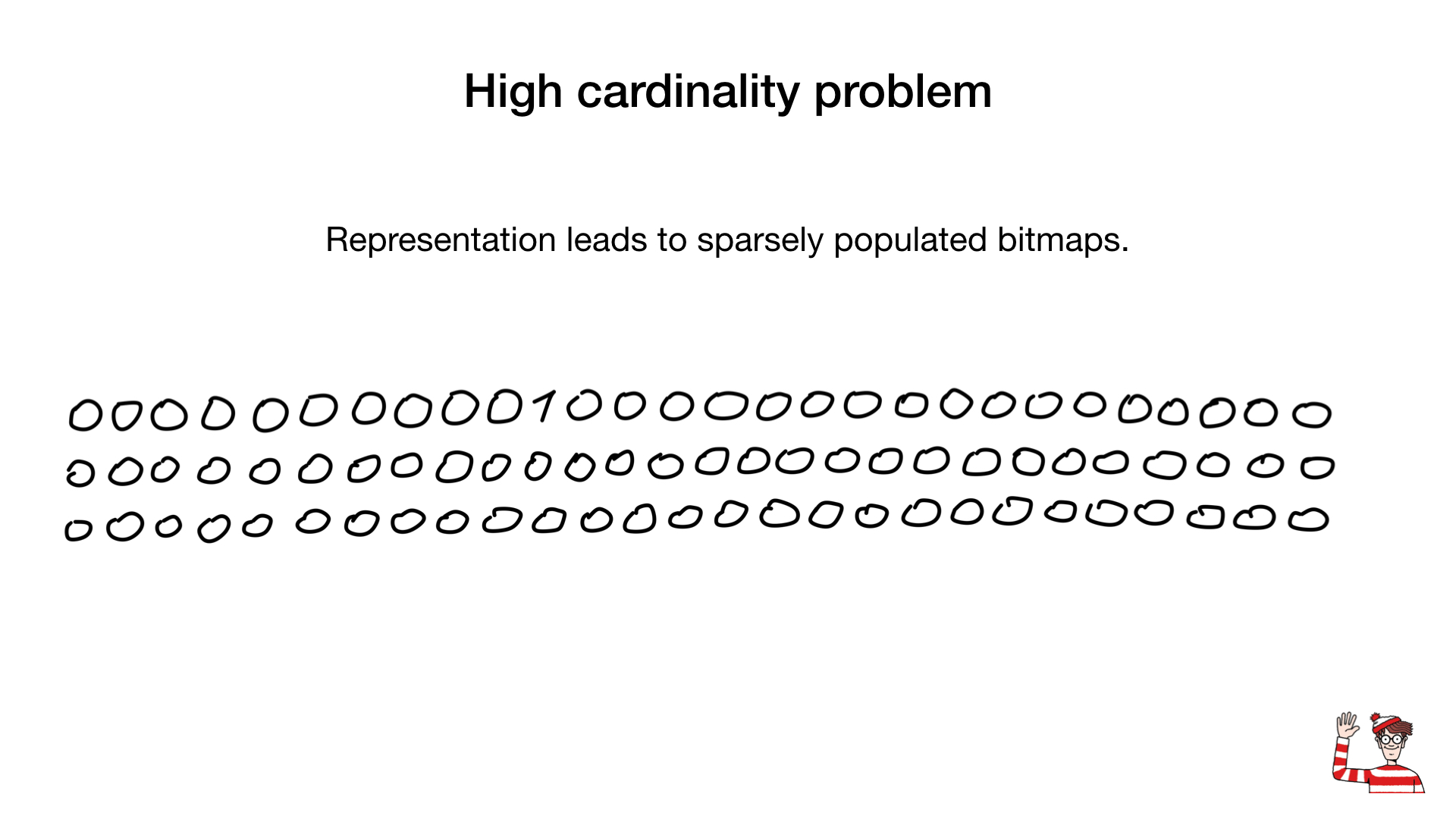
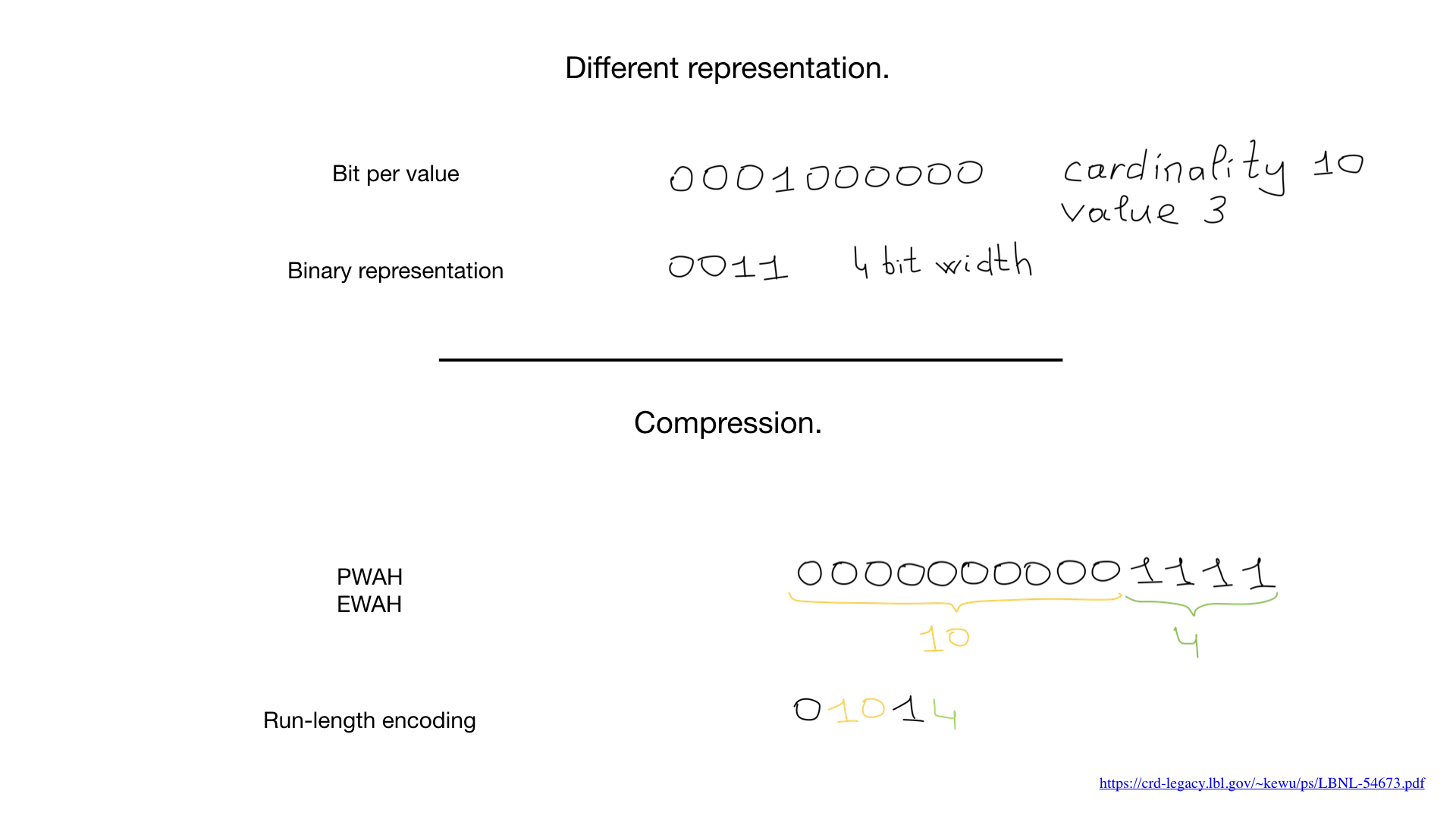
Sometimes we can use another representation, such as the standard one, which we use to represent numbers. But it was the appearance of compression algorithms that changed everything. Over the past decades, scientists and researchers have come up with a large number of compression algorithms for bitmaps. Their main advantage is that there is no need to compress bitmaps for performing bit operations - we can perform bit operations directly on compressed bitmaps.

Recently, hybrid approaches have begun to appear, such as, for example, roaring bitmaps. They use three different representations for bitmaps at the same time — the bitmaps themselves, arrays and so-called bit runs — and balance between them to maximize performance and minimize memory consumption.
You can find roaring bitmaps in the most popular applications. There are already a huge number of implementations for various programming languages, including more than three implementations for Go.
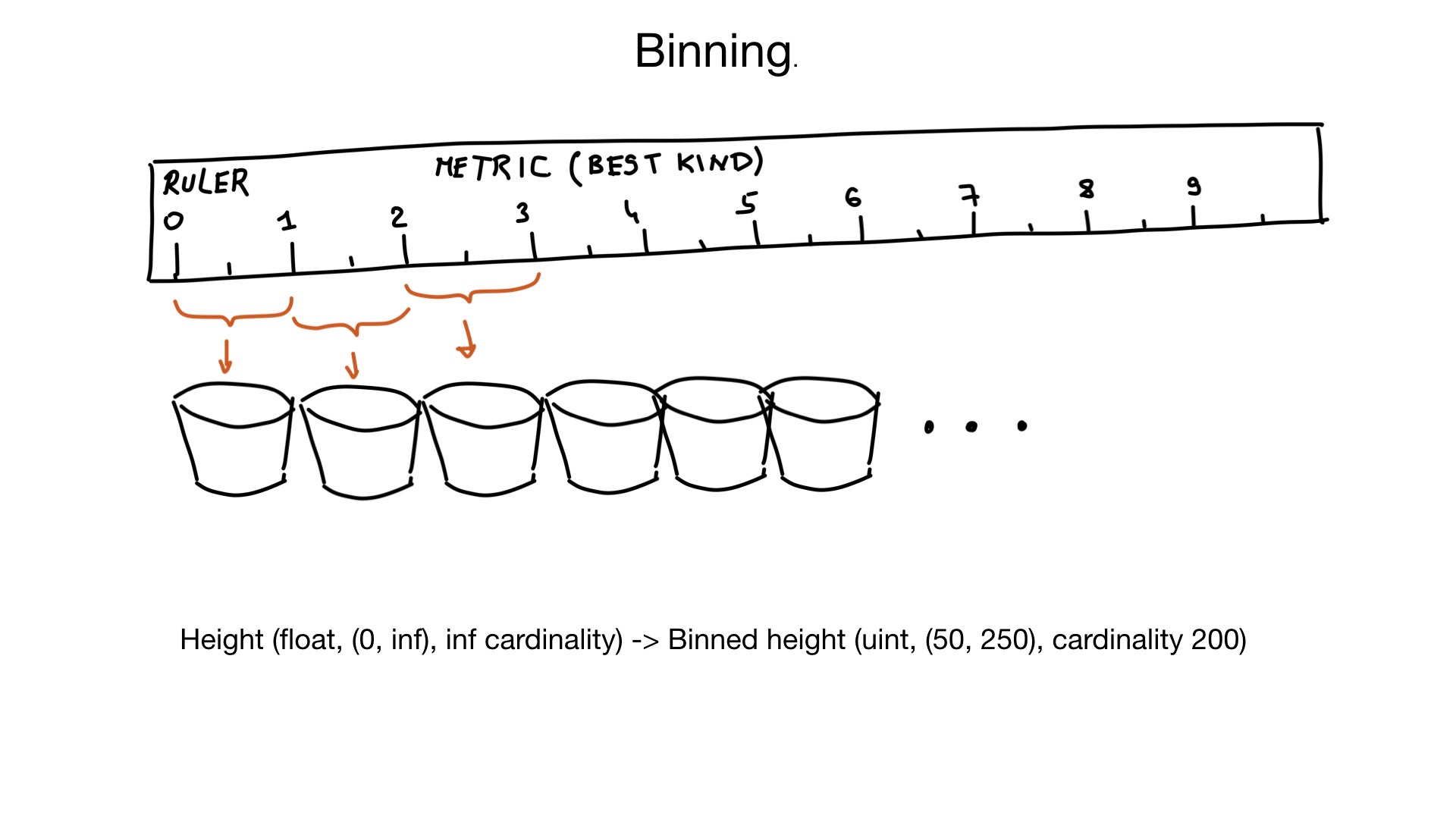
Another approach that can help us cope with great cardinality is binning. Imagine that you have a field that represents the height of a person. Growth is a floating point number, but we humans do not think about it in that way. For us there is no difference between the growth of 185.2 cm and 185.3 cm.
It turns out that we can group similar values into groups within 1 cm.
And if we also know that very few people have a height of less than 50 cm and more than 250 cm, then we can, in fact, turn a field with infinite cardinality into a field with cardinality of about 200 values.
Of course, if necessary, we can do additional filtering after.
High bandwidth problem
The next problem with bitmap indexes is that updating them can be very expensive.
Databases should allow data to be updated at the moment when hundreds of other queries potentially search for this data. We need locks to avoid simultaneous data access problems or other sharing problems. And where there is one big lock, there is a problem - lock contention, when this lock becomes a bottleneck.
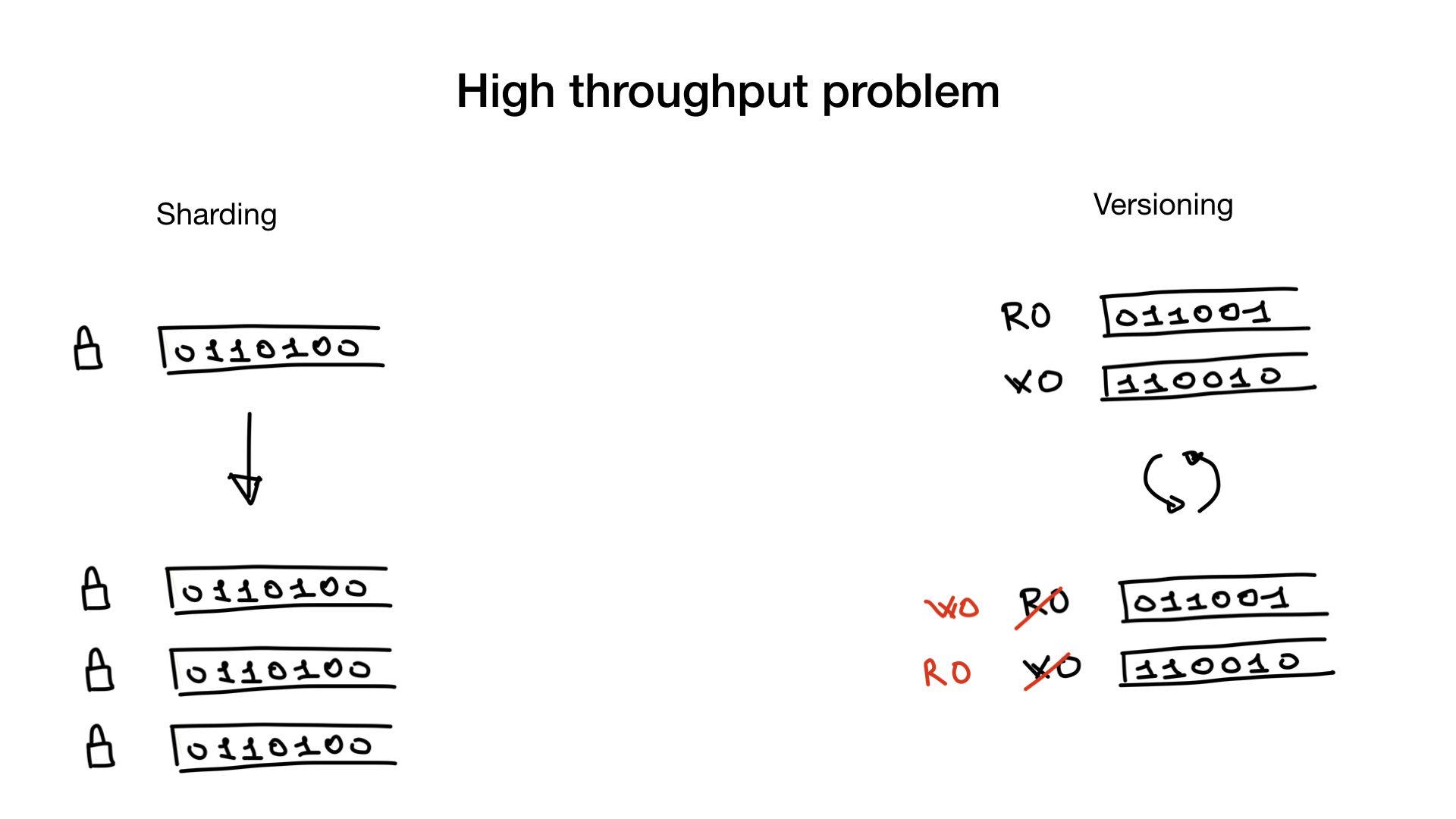
This problem can be solved or circumvented using sharding or using versioned indexes.
Sharding is a simple and well-known thing. You can shard the bitmap index as you would shard any other data. Instead of one big lock, you will get a bunch of small locks and thus get rid of lock contention.
The second way to solve the problem is to use versioned indexes. You can have one copy of the index that you use to search or read, and one to write or update. And once in a certain period of time (for example, once in 100 ms or 500 ms), you duplicate them and swap them. Of course, this approach is applicable only in cases where your application can work with a slightly lagging search index.
These two approaches can be used at the same time: you can have a shard versioned index.
More complex queries
The last problem with bitmap-indexes is that, as we are told, they are poorly suited for more complex types of queries, for example queries "by interval".
And the truth is, if you think bitwise operations like AND, OR, etc., are not very suitable for requests a la "Show me hotels with room rates from $ 200 to $ 300 per night."

A naive and very unwise decision would be to take the results for each dollar value and combine them with the OR bit operation.

A slightly better solution would be to use grouping. For example, in groups of $ 50. This would speed up our process 50 times.
But the problem is also easily solved using a view created specifically for this type of query. In scientific papers, it is called range-encoded bitmaps.

In this view, we do not just set one bit for any value (for example, 200), but set this value and everything above. 200 and higher. The same for 300: 300 and above. And so on.
Using this view, we can respond to this kind of search query, passing on the index only two times. First we get a list of hotels where the room costs less or $ 300, and then we throw out of it those where the cost of the room is less or $ 199. Is done.

, bitmap-. , , . , S2 Google. , . « » ( ).
Turnkey solutions
. - - , , .
, , bitmap- . , SIMD, .
, , .

Roaring
-, roaring bitmaps-, . , , bitmap-.
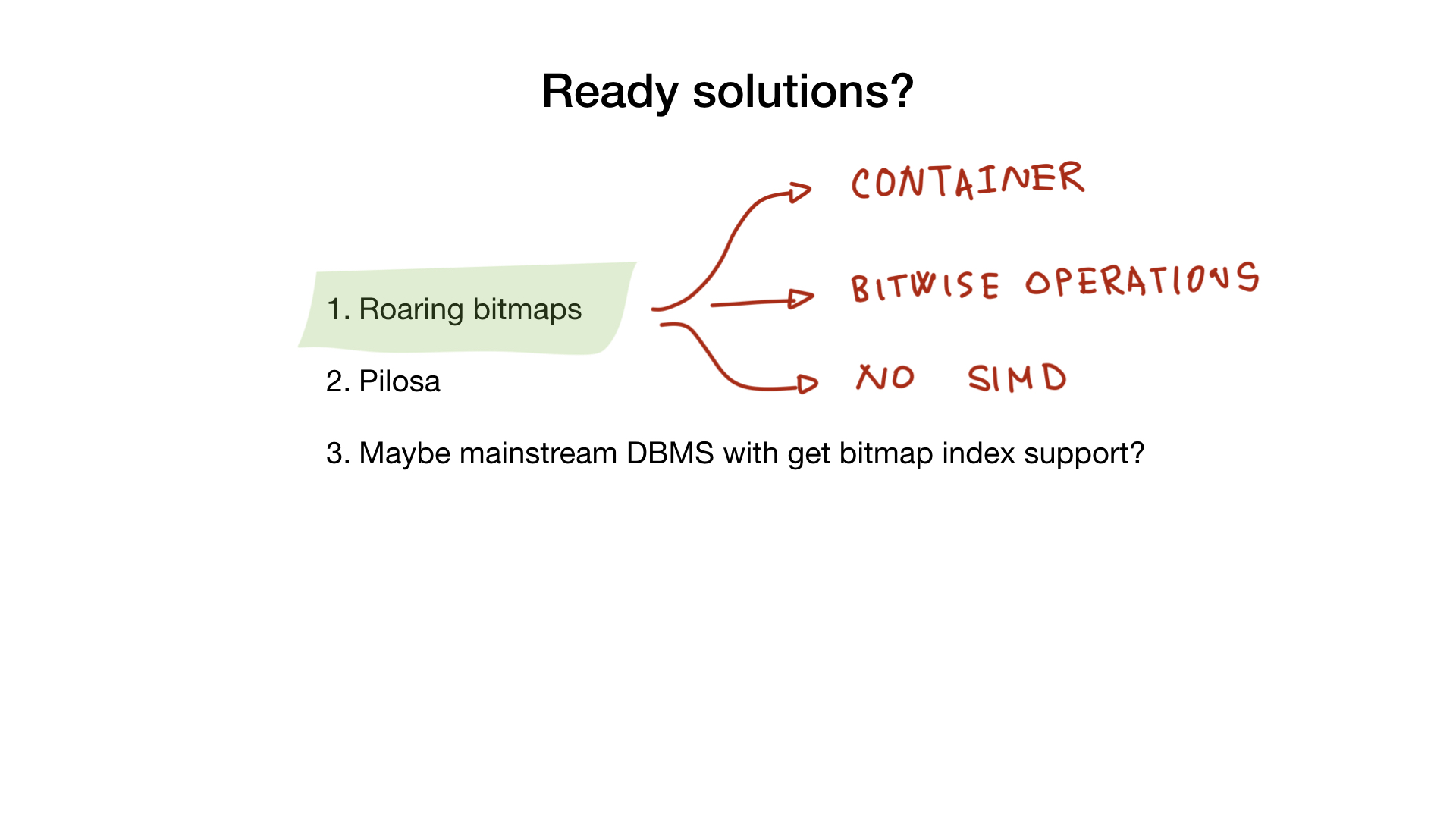
, Go- SIMD, , Go- , C, .
Pilosa
, , — Pilosa, , , bitmap- . , .
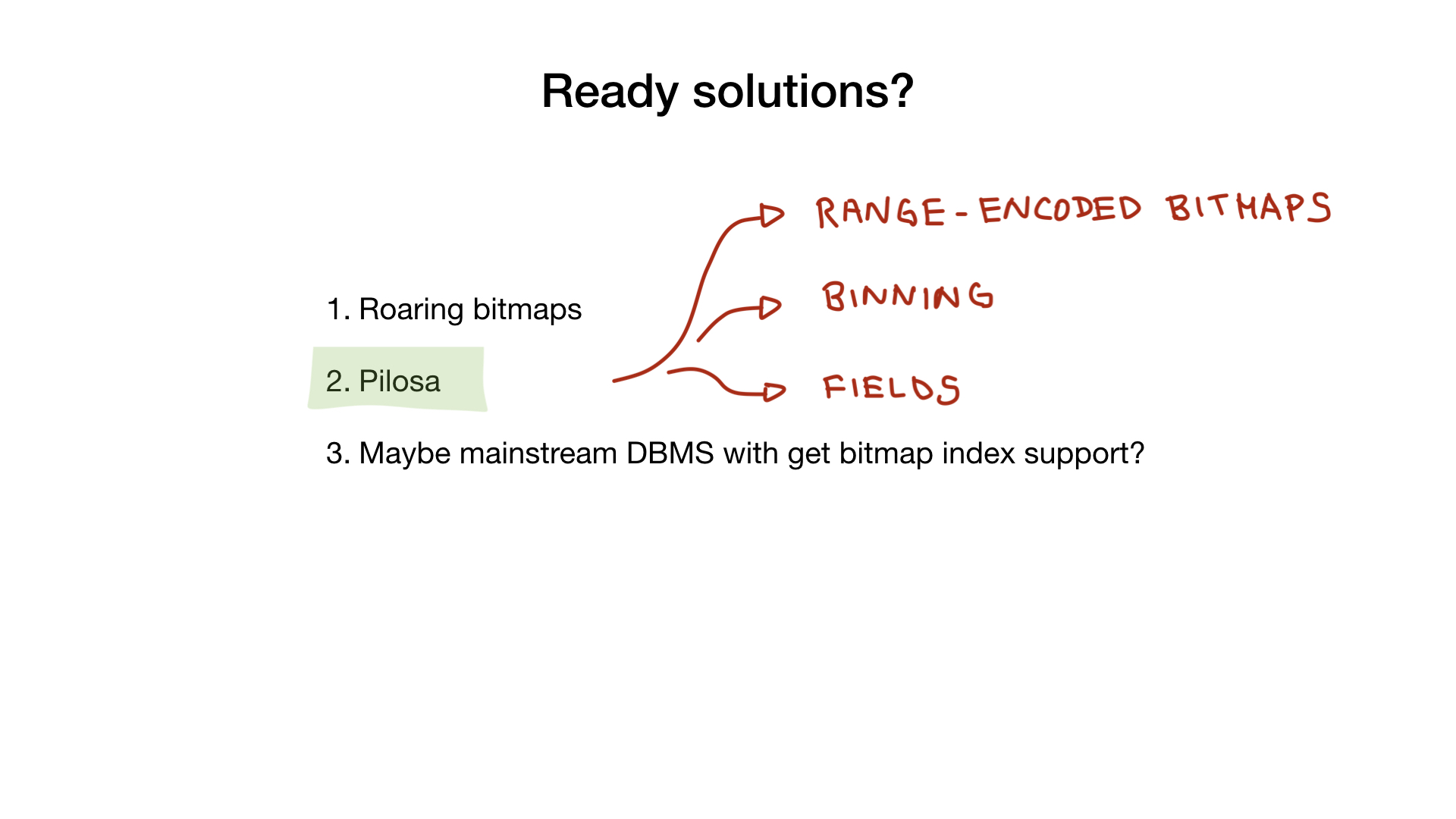
Pilosa roaring , , : , range-encoded bitmaps, . .
Pilosa .

, . Pilosa, , , , .
NOT «expensive», ( AND-) «terrace» «reservations». , .

, MySQL PostgreSQL — bitmap-.

Conclusion

, . - , , , , .
bitmap- , . .
Go , Go . Go.
, . Thank!
Source: https://habr.com/ru/post/451938/
All Articles