Wavelet analysis. Part 1
Introduction
Consider the discrete wavelet transform (DWT) implemented in the PyWavelets library PyWavelets 1.0.3 . PyWavelets is free open source software released under the MIT license.
When processing data on a computer, a sampled version of a continuous wavelet transform can be performed, the basics of which are described in my previous article . However, setting discrete values of parameters (a, b) of wavelets with an arbitrary step Δa and Δb requires a large number of calculations.
In addition, the result is an excess number of coefficients, far exceeding the number of samples of the original signal, which is not required for its reconstruction.
')
The discrete wavelet transform (DWT) implemented in the PyWavelets library provides enough information for both signal analysis and synthesis, being at the same time economical in the number of operations and in the required memory.
When to use wavelet transform instead of Fourier transform
Fourier transforms will work very well when the frequency spectrum is stationary. In this case, the frequencies present in the signal are independent of time, and the signal contains the xHz frequencies that are present in any place of the signal. The nonstationary signal, the worse the results will be. This is a problem, as most of the signals that we see in real life are non-stationary in nature.
The Fourier transform has a high resolution in the frequency domain, but zero resolution in the time domain. We show this in the following two examples.
Listing
import numpy as np from scipy import fftpack from pylab import* N=100000 dt = 1e-5 xa = np.linspace(0, 1, num=N) xb = np.linspace(0, 1/4, num=N/4) frequencies = [4, 30, 60, 90] y1a, y1b = np.sin(2*np.pi*frequencies[0]*xa), np.sin(2*np.pi*frequencies[0]*xb) y2a, y2b = np.sin(2*np.pi*frequencies[1]*xa), np.sin(2*np.pi*frequencies[1]*xb) y3a, y3b = np.sin(2*np.pi*frequencies[2]*xa), np.sin(2*np.pi*frequencies[2]*xb) y4a, y4b = np.sin(2*np.pi*frequencies[3]*xa), np.sin(2*np.pi*frequencies[3]*xb) def spectrum_wavelet(y): Fs = 1 / dt # sampling rate, Fs = 0,1 MHz n = len(y) # length of the signal k = np.arange(n) T = n / Fs frq = k / T # two sides frequency range frq = frq[range(n // 2)] # one side frequency range Y = fftpack.fft(y) / n # fft computing and normalization Y = Y[range(n // 2)] / max(Y[range(n // 2)]) # plotting the data subplot(2, 1, 1) plot(k/N , y, 'b') ylabel('Amplitude') grid() # plotting the spectrum subplot(2, 1, 2) plot(frq[0:140], abs(Y[0:140]), 'r') xlabel('Freq') plt.ylabel('|Y(freq)|') grid() y= y1a + y2a + y3a + y4a spectrum_wavelet(y) show() show() 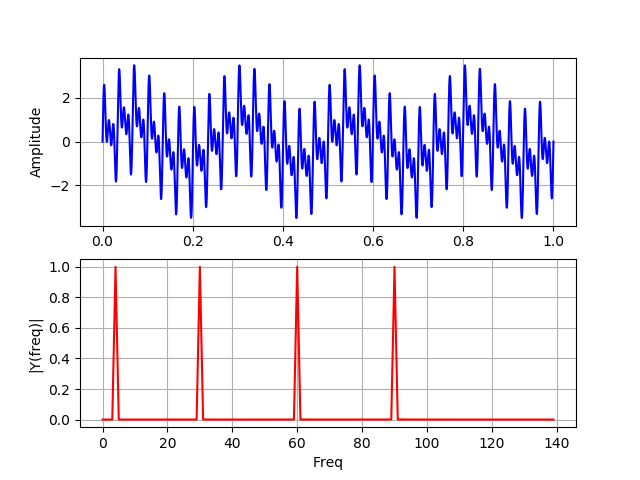
On this graph, all four frequencies are present in the signal throughout its duration.
Listing
import numpy as np from scipy import fftpack from pylab import* N=100000 dt = 1e-5 xa = np.linspace(0, 1, num=N) xb = np.linspace(0, 1/4, num=N/4) frequencies = [4, 30, 60, 90] y1a, y1b = np.sin(2*np.pi*frequencies[0]*xa), np.sin(2*np.pi*frequencies[0]*xb) y2a, y2b = np.sin(2*np.pi*frequencies[1]*xa), np.sin(2*np.pi*frequencies[1]*xb) y3a, y3b = np.sin(2*np.pi*frequencies[2]*xa), np.sin(2*np.pi*frequencies[2]*xb) y4a, y4b = np.sin(2*np.pi*frequencies[3]*xa), np.sin(2*np.pi*frequencies[3]*xb) def spectrum_wavelet(y): Fs = 1 / dt # sampling rate, Fs = 0,1 MHz n = len(y) # length of the signal k = np.arange(n) T = n / Fs frq = k / T # two sides frequency range frq = frq[range(n // 2)] # one side frequency range Y = fftpack.fft(y) / n # fft computing and normalization Y = Y[range(n // 2)] / max(Y[range(n // 2)]) # plotting the data subplot(2, 1, 1) plot(k/N , y, 'b') ylabel('Amplitude') grid() # plotting the spectrum subplot(2, 1, 2) plot(frq[0:140], abs(Y[0:140]), 'r') xlabel('Freq') plt.ylabel('|Y(freq)|') grid() y = np.concatenate([y1b, y2b, y3b, y4b]) spectrum_wavelet(y) show() show() 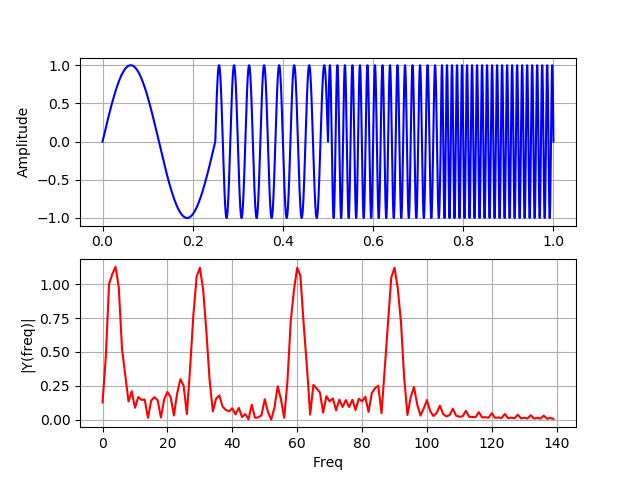
In this graph, the signals do not overlap in time, the side lobes are due to a gap between four different frequencies.
For two frequency spectra containing exactly the same four peaks, the Fourier transform cannot determine where these frequencies are present in the signal. The best approach for analyzing signals with a dynamic frequency spectrum is the wavelet transform.
The basic properties of wavelets
The choice of the type, and therefore the properties of the wavelet, depends on the task of analysis, for example, to determine the effective values of currents in the power industry, greater accuracy is provided by the wavelets of Ingrid Daubeci of large orders. The properties of the wavelets can be obtained using the pywt.DiscreteContinuousWavelet () function in the following listing:
Listing
import pywt from pylab import * from numpy import * discrete_wavelets = ['db5', 'sym5', 'coif5', 'haar'] print('discrete_wavelets-%s'%discrete_wavelets ) st='db20' wavelet = pywt.DiscreteContinuousWavelet(st) print(wavelet) i=1 phi, psi, x = wavelet.wavefun(level=i) subplot(2, 1, 1) title(" - -%s"%st) plot(x,psi,linewidth=2, label='level=%s'%i) grid() legend(loc='best') subplot(2, 1, 2) title(" - -%s"%st) plt.plot(x,phi,linewidth=2, label='level=%s'%i) legend(loc='best') grid() show() We get:
discrete_wavelets - ['db5', 'sym5', 'coif5', 'haar']
Wavelet db20 Family name: Daubechies Short name: db Filters length: 40 Orthogonal: True Biorthogonal: True Symmetry: asymmetric DWT: True CWT: False 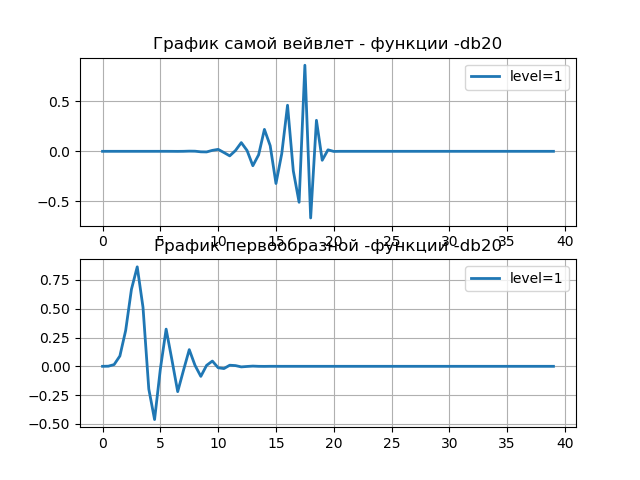
In a number of practical cases, it is necessary to obtain information about the center frequency of the psi wavelet — a function that is used, for example, in wavelet analysis of signals to identify defects in gears:
import pywt f=pywt.central_frequency('haar', precision=8 ) print(f) # : scale=1 f1=pywt.scale2frequency('haar',scale) print(f1) 0.9961089494163424 0.9961089494163424 Using the center frequency maternal wavelet and scale factor "a" can convert scales to pseudo frequencies using the equation:
Signal Expansion Modes
Before computing a discrete wavelet transform using filter banks , it becomes necessary to lengthen the signal . Depending on the extrapolation method, significant artifacts can occur at the signal boundaries, leading to inaccurate DWT conversion.
PyWavelets provides several signal extrapolation methods that can be used to minimize this negative effect. To demonstrate these methods, use the following listing:
Listing demonstration of signal extension methods
import numpy as np from matplotlib import pyplot as plt from pywt._doc_utils import boundary_mode_subplot # synthetic test signal x = 5 - np.linspace(-1.9, 1.1, 9)**2 # Create a figure with one subplots per boundary mode fig, axes = plt.subplots(3, 3, figsize=(10, 6)) plt.subplots_adjust(hspace=0.5) axes = axes.ravel() boundary_mode_subplot(x, 'symmetric', axes[0], symw=False) boundary_mode_subplot(x, 'reflect', axes[1], symw=True) boundary_mode_subplot(x, 'periodic', axes[2], symw=False) boundary_mode_subplot(x, 'antisymmetric', axes[3], symw=False) boundary_mode_subplot(x, 'antireflect', axes[4], symw=True) boundary_mode_subplot(x, 'periodization', axes[5], symw=False) boundary_mode_subplot(x, 'smooth', axes[6], symw=False) boundary_mode_subplot(x, 'constant', axes[7], symw=False) boundary_mode_subplot(x, 'zeros', axes[8], symw=False) plt.show() 
The graphs show how a short signal (red) expands (black) beyond its original length.
Discrete Wavelet Transform
To demonstrate the DWT, we will use a signal with a dynamic frequency spectrum, which increases with time. The beginning of the signal contains low-frequency values, and the end of the signal contains frequencies of the shortwave range. This allows us to easily determine which part of the frequency spectrum is filtered out simply by looking at the time axis:
Listing
from pylab import * from numpy import* x = linspace(0, 1, num=2048) chirp_signal = sin(250 * pi * x**2) fig, ax = subplots(figsize=(6,1)) ax.set_title(" ") ax.plot(chirp_signal) show() 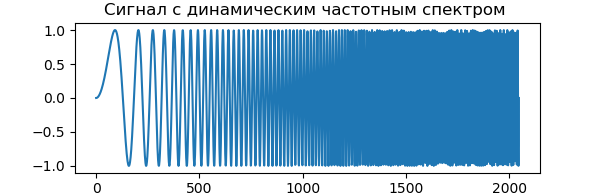
The discrete wavelet transform in PyWavelets 1.0.3 is the pywt.dwt () function, which calculates the approximating coefficients cA and the detail cD coefficients of the first level of the wavelet transform of a signal given by a vector:
Listing first level conversion
import pywt from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' (cA, cD) = pywt.dwt(y,st) subplot(2, 1, 1) plot(cA,'b',linewidth=2, label='cA,level-1') grid() legend(loc='best') subplot(2, 1, 2) plot(cD,'r',linewidth=2, label='cD,level-1') grid() legend(loc='best') show() 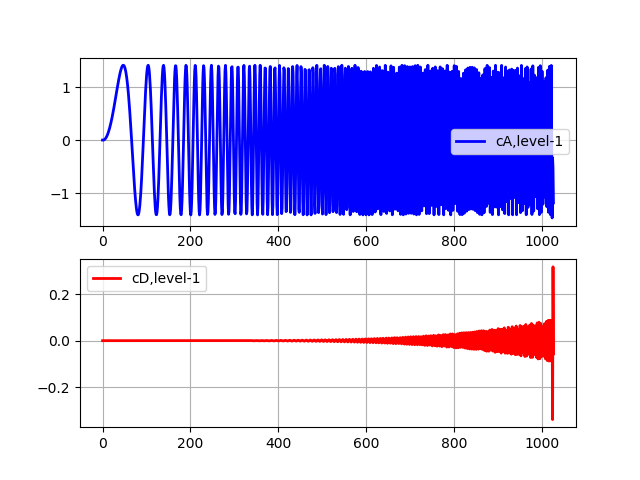
Listing fifth level conversion
import pywt from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' (cA, cD) = pywt.dwt(y,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) subplot(2, 1, 1) plot(cA,'b',linewidth=2, label='cA,level-5') grid() legend(loc='best') subplot(2, 1, 2) plot(cD,'r',linewidth=2, label='cD,level-5') grid() legend(loc='best') show() 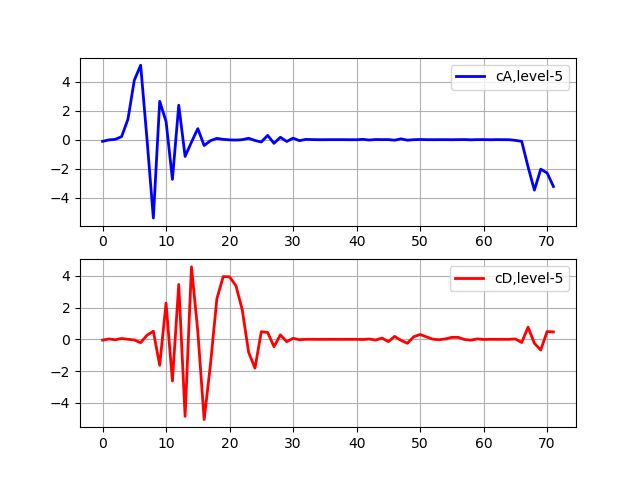
The approximation coefficients (cA) represent the output of the low-pass filter (averaging filter) DWT. The detail coefficients (cD) represent the output of the high-pass filter (differential filter) DWT.
You can use the pywt.wavedec () function to immediately calculate higher level coefficients. This function takes as input the source signal and the level and returns one set of approximation coefficients (n-th level) and n sets of detail coefficients (from 1 to n-th level). Here is an example for level five:
from pywt import wavedec from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' coeffs = wavedec(y, st, level=5) subplot(2, 1, 1) plot(coeffs[0],'b',linewidth=2, label='cA,level-5') grid() legend(loc='best') subplot(2, 1, 2) plot(coeffs[1],'r',linewidth=2, label='cD,level-5') grid() legend(loc='best') show() As a result, we get the same graphs as in the previous example. You can get separately the coefficients cA and cD:
For cA:
import pywt from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data = sin (250 * pi * x**2) coefs=pywt.downcoef('a', data, 'db20', mode='symmetric', level=1) For cD:
import pywt from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data = sin (250 * pi * x**2) coefs=pywt.downcoef('d', data, 'db20', mode='symmetric', level=1) Filter bank
We discussed some of the issues related to conversion levels in the previous section. However, DWT is always implemented as a filter bank in the form of a cascade of high-frequency and low-frequency filters. Filter banks are a very effective way of splitting a signal into several frequency subbands.
At the first stage with a small scale analyzing the high-frequency signal behavior. At the second stage, the scale increases by a factor of two (the frequency decreases by a factor of two), and we analyze the behavior of about half of the maximum frequency. At the third stage, the scale factor is equal to four, and we analyze the frequency behavior of about a quarter of the maximum frequency. And this continues until we reach the maximum level of decomposition.
The maximum level of decomposition can be calculated using the pywt.wavedec () function, while decomposition and detailing will look like this:
Listing
import pywt from pywt import wavedec from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data= sin (250 * pi * x**2) n_level=pywt.dwt_max_level(len(data), 'sym5') print(' : %s'%n_level) x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' coeffs = wavedec(y, st, level=7) subplot(2, 1, 1) plot(coeffs[0],'b',linewidth=2, label='cA,level-7') grid() legend(loc='best') subplot(2, 1, 2) plot(coeffs[1],'r',linewidth=2, label='cD,level-7') grid() legend(loc='best') show() We get:
Maximum level of decomposition: 7
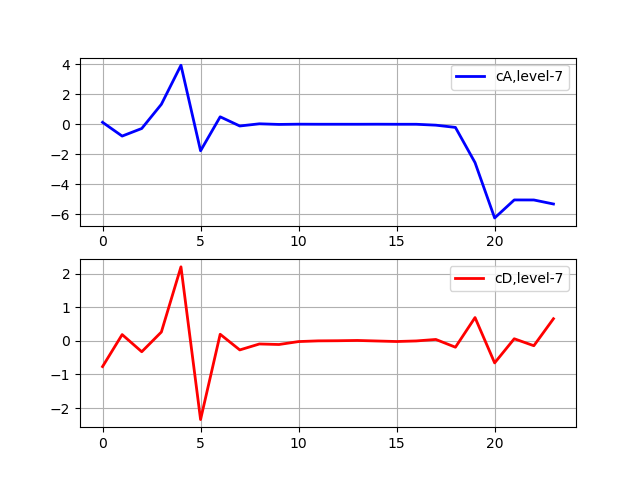
The decomposition stops when the signal becomes shorter than the filter length for a given sym5 wavelet. For example, suppose we have a signal with frequencies up to 1000 Hz. At the first stage, we divide our signal into low-frequency and high-frequency parts, i.e. 0-500 Hz and 500-1000 Hz. At the second stage, we take the low-frequency part and again divide it into two parts: 0-250 Hz and 250-500 Hz. In the third stage, we divided the part of 0-250 Hz into part of 0-125 Hz and part of 125-250 Hz. This continues until we reach the maximum level of decomposition.
Analysis of wav files using fft Fourier and wavelet scalars
For the analysis we will use the WebSDR file . Consider the analysis of the reduced signal by means of triang from scipy.signal and the implementation of the discrete Fourier transform in python (fft from scipy.fftpack). If the length of the fft sequence is not equal to 2n, then instead of the fast Fourier transform (fft), a discrete Fourier transform (dft) will be performed. This is how this command works.
We use the fast Fourier transform buffer according to the following scheme (numerical data for an example):
fftbuffer = np.zeros (15); create a buffer filled with zeros;
fftbuffer [: 8] = x [7:]; move the end of the signal to the first part of the buffer; fftbuffer [8:] = x [: 7] —shifts the start of the signal to the last part of the buffer; X = fft (fftbuffer) - consider the Fourier transform of the buffer filled with the signal values.
To make the phase spectrum more readable, apply phase deployment. To do this, change the line with the calculation of the phase characteristics: pX = np.unwrap (np.angle (X)).
Listing for fft signal fragment analysis
import numpy as np from pylab import * from scipy import * import scipy.io.wavfile as wavfile M=501 hM1=int(np.floor((1+M)/2)) hM2=int(np.floor(M/2)) (fs,x)=wavfile.read('WebSDR.wav') x1=x[5000:5000+M]*np.hamming(M) N=511 fftbuffer=np.zeros([N]) fftbuffer[:hM1]=x1[hM2:] fftbuffer[N-hM2:]=x1[:hM2] X=fft(fftbuffer) mX=abs(X) pX=np.angle(X) suptitle(" WebSDR") subplot(3, 1, 1) st=' (WebSDR.wav)' plot(x,linewidth=2, label=st) legend(loc='center') subplot(3, 1, 2) st=' ' plot(mX,linewidth=2, label=st) legend(loc='best') subplot(3, 1, 3) st=' ' pX=np.unwrap(np.angle(X)) plot(pX,linewidth=2, label=st) legend(loc='best') show() 
For a comparative analysis, we will use the wavelet scalar , which can be constructed using the function tree = pywt.wavedec (signal, 'coif5') in matplotlib.
Wavelet Waveform Listing
from pylab import * import pywt import scipy.io.wavfile as wavfile # , . def lepow2(x): return int(2 ** floor(log2(x))) # MRA. def scalogram(data): bottom = 0 vmin = min(map(lambda x: min(abs(x)), data)) vmax = max(map(lambda x: max(abs(x)), data)) gca().set_autoscale_on(False) for row in range(0, len(data)): scale = 2.0 ** (row - len(data)) imshow( array([abs(data[row])]), interpolation = 'nearest', vmin = vmin, vmax = vmax, extent = [0, 1, bottom, bottom + scale]) bottom += scale # , . rate, signal = wavfile.read('WebSDR.wav') signal = signal[0:lepow2(len(signal))] tree = pywt.wavedec(signal, 'coif5') gray() scalogram(tree) show() 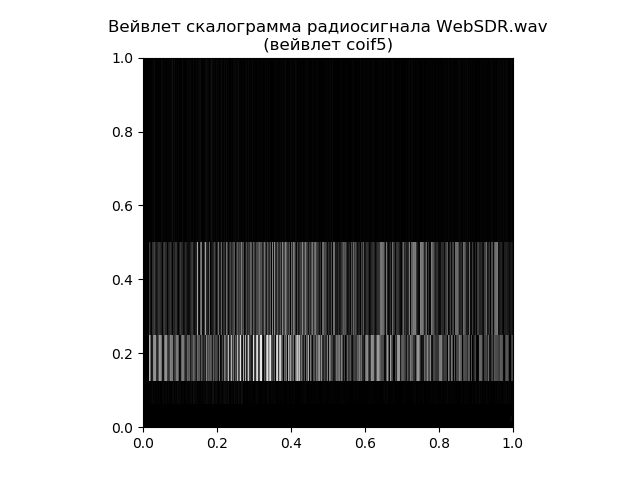
Thus, scalogram gives a more detailed answer to the question of the distribution of frequencies over time, and the fast Fourier transform is responsible for the frequencies themselves. It all depends on the task, even for such a simple example.
findings
- The rationale for using discrete wavelet transforms for dynamic signals is given.
- Examples of wavelet analysis using PyWavelets 1.0.3, open source software released under the MIT license, are given.
- Software tools for practical use of the PyWavelets library are considered.
Source: https://habr.com/ru/post/451278/
All Articles