Hi workers. I will not detain your attention for a long time with an explanation of the declarative approach, I will try to propose to solve another problem using a logic programming language, as a variant of a declarative look at the formulation of problems and their solutions.

Problem 391. Perfect Rectangle

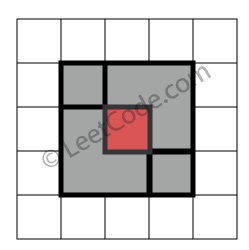
Given N axis-aligned rectangles where N> 0, determine if it is a rectangular region.
Each rectangle is represented as a bottom-left point and a top-right point. For example, a unit square is represented as [1,1,2,2]. (coordinate of bottom-left point is (1, 1) and top-right point is (2, 2)).

Example 1: rectangles = [
[1,1,3,3],
[3,1,4,2],
[3,2,4,4]
[1,3,2,4],
[2,3,3,4]]
Return true. All 5 rectangles together form a rectangular region.
...
Example 3: rectangles =
[[1,1,3,3],
[3,1,4,2],
[1,3,2,4],
[3,2,4,4]]
Return false. Because there is a gap in the top center.

Thinking about the formulation takes place the second day, this is certainly not weekly classes on the inclusion of vintage lamps , but still I want to present the results of the work on the task. It took several attempts to solve all the available tests.

The initial data is represented by a list, let me remind you briefly, the list is [Head | Tail], where the Tail is a list, and the list is also empty [] .

Formulate 1

It is necessary to calculate the total area of ​​all the rectangles, find the maximum size of the rectangle describing all of them, and check these two sums, if it is equal, then all the rectangles cover the area evenly. At the same time, we check that the rectangles do not intersect, we will add each new rectangle to the list, it should not overlap and intersect all previous ones.

To do this, I apply tail recursion (the same, recursion on the descent), the most "imperative" way to represent a cycle. In one such "cycle", we immediately find the total amount of areas and the minimum left and maximum right angle of the describing rectangle, hike, accumulating a general list of figures, checking that there are no intersections.

Like this:

findsum([], Sres,Sres,LConerRes,LConerRes,RConerRes,RConerRes,_). findsum([[Lx,Ly,Rx,Ry]|T], Scur,Sres,LConerCur,LConerRes,RConerCur,RConerRes,RectList):- mincon(Lx:Ly,LConerCur,LConerCur2), maxcon(Rx:Ry,RConerCur,RConerCur2), Scur2 is Scur+(Rx-Lx)*(Ry-Ly), not(chekin([Lx,Ly,Rx,Ry],RectList)), findsum(T, Scur2,Sres,LConerCur2,LConerRes,RConerCur2,RConerRes,[[Lx,Ly,Rx,Ry]|RectList]). 

In Prolog, variables are unknown, they cannot be changed, they are either empty or accept a value, a couple of variables are required from here, initial and resultant, when we reach the end of the list, the current value will become the resultant (first line of the rule). Unlike imperative languages, for support understanding the program line you need to imagine the whole path that led to it, and all variables can have their own “history” of accumulation, right there, each line of the program only in the context of the current rule, the whole state that influenced it on the face entry rules.

So:

 %   mincon(X1:Y1,X2:Y2,X1:Y1):-X1=<X2,Y1=<Y2,!. mincon(_,X2:Y2,X2:Y2). %  maxcon(X1:Y1,X2:Y2,X1:Y1):-X1>=X2,Y1>=Y2,!. maxcon(_,X2:Y2,X2:Y2). 

Here, the "structured term" of the form X: Y is used to represent the angle; it is an opportunity to combine several values ​​into a structure, a tuple, so to speak, only a functor can be any operation. And the cut-off “!”, Allows not specifying the condition in the second line of the rule, it is a way to increase the efficiency of calculations.

And as it turned out, the most important thing is to check the non-intersection of rectangles, they accumulate in the list:

 %    chekin(X,[R|_]):-cross(X,R),!. chekin(X,[_|T]):-chekin(X,T). %     ,    cross(X,X):-!. cross(X,Y):-cross2(X,Y),!. cross(X,Y):-cross2(Y,X). %,       cross2([X11,Y11,X12,Y12],[X21,Y21,X22,Y22]):-X11<X22,X22=<X12,Y11<Y22,Y22=<Y12,!.%rt cross2([X11,Y11,X12,Y12],[X21,Y21,X22,Y22]):-X11=<X21,X21<X12,Y11<Y22,Y22=<Y12,!.%lt cross2([X11,Y11,X12,Y12],[X21,Y21,X22,Y22]):-X11<X22,X22=<X12,Y11=<Y21,Y21<Y12,!.%rb cross2([X11,Y11,X12,Y12],[X21,Y21,X22,Y22]):-X11=<X21,X21<X12,Y11=<Y21,Y21<Y12. %lb 

The intersection of rectangles, these are four options for getting the top of the first inside the other.

And the final statement:

 isRectangleCover(Rects):- [[Lx,Ly,Rx,Ry]|_]=Rects, findsum(Rects,0,S,Lx:Ly,LconerX:LconerY,Rx:Ry,RconerX:RconerY,[]),!, S=:= (RconerX-LconerX)*(RconerY-LconerY). 

At the entrance there is a list of figures, first we take for the initial values ​​of the left and right angle, we perform a detour of all, having calculated the total area, and check the obtained sums. I note that if the intersection of the rectangles occurred, then the search for the amount "refuses", returns the "falls", which means that there is nothing to verify the amounts. The same happens if there are no figures in the input list, there will be a failure, there is nothing to compare ...

Further, this implementation, I run on the available tests, I cite the first 40:

 %unit-tests framework assert_are_equal(Goal, false):-get_time(St),not(Goal),!,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, true):- get_time(St),Goal, !,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, Exp):-writeln(Goal->failed:expected-Exp). :-assert_are_equal(isRectangleCover([[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]),true). :-assert_are_equal(isRectangleCover([[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]),false). :-assert_are_equal(isRectangleCover([[1,1,3,3],[3,1,4,2],[1,3,2,4],[3,2,4,4]]),false). :-assert_are_equal(isRectangleCover([[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]),false). :-assert_are_equal(isRectangleCover([[0,0,4,1],[0,0,4,1]]),false). 

 :-assert_are_equal(isRectangleCover([[0,0,4,1],[7,0,8,2],[6,2,8,3],[5,1,6,3],[4,0,5,1],[6,0,7,2],[4,2,5,3],[2,1,4,3],[0,1,2,2],[0,2,2,3],[4,1,5,2],[5,0,6,1]]),true). :-assert_are_equal(isRectangleCover([[0,0,4,1],[7,0,8,2],[5,1,6,3],[6,0,7,2],[4,0,5,1],[4,2,5,3],[2,1,4,3],[0,2,2,3],[0,1,2,2],[6,2,8,3],[5,0,6,1],[4,1,5,2]]),true). :-assert_are_equal(isRectangleCover([[0,0,4,1]]),true). :-assert_are_equal(isRectangleCover([[0,0,3,3],[1,1,2,2]]),false). :-assert_are_equal(isRectangleCover([[1,1,2,2],[1,1,2,2],[2,1,3,2]]),false). :-assert_are_equal(isRectangleCover([[0,0,1,1],[0,1,3,2],[1,0,2,2]]),false). :-assert_are_equal(isRectangleCover([[0,0,1,1],[0,1,1,2],[0,2,1,3],[0,3,1,4]]),true). :-assert_are_equal(isRectangleCover([[0,0,1,1],[1,0,2,1],[2,0,3,1],[3,0,4,1]]),true). :-assert_are_equal(isRectangleCover([[0,0,2,2],[1,1,3,3],[2,0,3,1],[0,3,3,4]]),false). :-assert_are_equal(isRectangleCover([[0,0,3,1],[0,1,2,3],[1,0,2,1],[2,2,3,3]]),false). :-assert_are_equal(isRectangleCover([[1,1,3,3],[2,2,4,4],[4,1,5,4],[1,3,2,4]]),false). :-assert_are_equal(isRectangleCover([[0,0,1,1],[0,0,2,1],[1,0,2,1],[0,2,2,3]]),false). :-assert_are_equal(isRectangleCover([[0,0,2,1],[0,1,2,2],[0,2,1,3],[1,0,2,1]]),false). :-assert_are_equal(isRectangleCover([[1,1,2,2],[0,1,1,2],[1,0,2,1],[0,2,3,3],[2,0,3,3]]),false). :-assert_are_equal(isRectangleCover([[0,0,4,1],[7,0,8,2],[6,2,8,3],[5,1,6,3],[6,0,7,2],[4,2,5,3],[2,1,4,3],[0,1,2,2],[0,2,2,3],[4,1,5,2],[5,0,6,1]]),false). :-assert_are_equal(isRectangleCover([[0,0,4,1],[7,0,8,2],[5,1,6,4],[6,0,7,2],[4,0,5,1],[4,2,5,3],[2,1,4,3],[0,2,2,3],[0,1,2,2],[6,2,8,3],[5,0,6,1],[4,1,5,2]]),false). :-assert_are_equal(isRectangleCover([[0,0,4,1],[7,0,8,3],[5,1,6,3],[6,0,7,2],[4,0,5,1],[4,2,5,3],[2,1,4,3],[0,2,2,3],[0,1,2,2],[6,2,8,3],[5,0,6,1],[4,1,5,2]]),false). :-assert_are_equal(isRectangleCover([[0,0,5,1],[7,0,8,2],[5,1,6,3],[6,0,7,2],[4,0,5,1],[4,2,5,3],[2,1,4,3],[0,2,2,3],[0,1,2,2],[6,2,8,3],[5,0,6,1],[4,1,5,2]]),false). :-assert_are_equal(isRectangleCover([[0,0,1,1],[0,0,1,1],[0,2,1,3]]),false). :-assert_are_equal(isRectangleCover([[0,0,3,3],[1,1,2,2],[1,1,2,2]]),false). :-assert_are_equal(isRectangleCover([[1,1,4,4],[1,3,4,5],[1,6,4,7]]),false). :-assert_are_equal(isRectangleCover([[0,0,3,1],[0,1,2,3],[2,0,3,1],[2,2,3,3]]),false). :-assert_are_equal(isRectangleCover([[0,0,1,1],[0,0,1,1],[1,1,2,2],[1,1,2,2]]),false). :-assert_are_equal(isRectangleCover([[1,1,2,2],[1,1,2,2],[1,1,2,2],[2,1,3,2],[2,2,3,3]]),false). :-assert_are_equal(isRectangleCover([[1,1,2,2],[2,1,3,2],[2,1,3,2],[2,1,3,2],[3,1,4,2]]),false). :-assert_are_equal(isRectangleCover([[0,1,2,3],[0,1,1,2],[2,2,3,3],[1,0,3,1],[2,0,3,1]]),false). :-assert_are_equal(isRectangleCover([[0,0,1,1],[0,2,1,3],[1,1,2,2],[2,0,3,1],[2,2,3,3],[1,0,2,3],[0,1,3,2]]),false). :-assert_are_equal(isRectangleCover([[0,0,1,1],[0,0,1,1],[0,0,1,1],[0,0,1,1],[0,0,1,1],[0,0,1,1],[0,0,1,1],[0,0,1,1],[2,2,3,3]]),false). :-assert_are_equal(isRectangleCover([[0,0,1,1],[0,1,1,2],[0,2,1,3],[1,0,2,1],[1,0,2,1],[1,2,2,3],[2,0,3,1],[2,1,3,2],[2,2,3,3]]),false). :-assert_are_equal(isRectangleCover([[0,0,4,1],[7,0,8,2],[5,1,6,3],[6,0,7,2],[2,1,4,3],[0,2,2,3],[0,1,2,2],[6,2,8,3],[5,0,6,1]]),false). :-assert_are_equal(isRectangleCover([[0,0,4,1],[7,0,8,2],[5,1,6,3],[6,0,7,2],[4,0,5,1],[4,2,5,3],[2,1,4,3],[-1,2,2,3],[0,1,2,2],[6,2,8,3],[5,0,6,1],[4,1,5,2]]),false). :-assert_are_equal(isRectangleCover([[0,0,1,1],[1,0,2,1],[1,0,3,1],[3,0,4,1]]),false). :-assert_are_equal(isRectangleCover([[1,2,4,4],[1,0,4,1],[0,2,1,3],[0,1,3,2],[3,1,4,2],[0,3,1,4],[0,0,1,1]]),true). 

And this is not the end, the task from the hard section, in 41 tests they offer a list of 10,000 rectangles, in all the last five tests I get these times in seconds:

 test 41:length=10000 goal->ok:212/sec test 42:length=3982 goal->ok:21/sec test 43:length=10222 goal->ok:146/sec test 44:length=10779 goal->ok:41/sec test 45:length=11000 goal->ok:199/sec 

I cannot bring in incoming values, they do not fit into the editor, I attach test 41 like this.

Formulation 2

The previous approach, to use the list for the accumulation of figures, turns out to be very inefficient, what kind of change suggests itself - instead of the complexity n ^ 2, make n * log (n). You can use a tree to check the intersections of the list of rectangles.

A binary tree for Prolog is also a structured term, and as a list it is recursively defined, the tree is empty or contains a value and two subtrees .

I use the triple functor for this: t (LeftTree, RootValue, RightTree), and the empty tree will be [].

A simple tree of numbers, with smaller ordering on the left and larger ones, can be expressed like this:

 add_to_tree(X,[],t([],X,[])). add_to_tree(X,t(L,Root,R),t(L,Root,NewR)):- X<Root,!,add_to_tree(X,R,NewR). add_to_tree(X,t(L,Root,R),t(NewL,Root,R)):- add_to_tree(X,L,NewL). 

In the classic book of I. Bratko "Programming in the Prologue for Artificial Intelligence" there are a lot of implementations of trees 2-3, balanced AVL ...

I suggest solving the ordering of rectangles as follows: if the rectangle is to the right of the other, then they do not intersect, and those to the left should be checked for intersection. And to the right, this is when the right angle of one is less than the left corner of the second:

 righter([X1,_,_,_],[_,_,X2,_]):-X1>X2. 

And the task of accumulating figures in a tree, plus checking for an intersection may look like this, when a new rectangle is to the right of the one located in the root, then it is necessary to check on the right otherwise to check the intersections on the left:

 treechk(X,[],t([],X,[])). treechk([X1,Y1,X2,Y2],t(L,[X1,Y11,X2,Y22],R),t(L,[X1,Yr,X2,Yr2],R)):- (Y1=Y22;Y2=Y11),!,Yr is min(Y1,Y11),Yr2 is max(Y2,Y22). %union treechk(X,t(L,Root,R),t(L,Root,NewR)):- righter(X,Root),!,treechk(X,R,NewR). treechk(X,t(L,Root,R),t(NewL,Root,R)):- not(cross(X,Root)),treechk(X,L,NewL). 

Immediately considered another cunning If the rectangles are the same width, and have a common face, they can be combined into one and not added to the tree, but simply change the size of the rectangle in one node. This pushes test 41, there is this type of data: [[0, -1,1,0], [0,0,1,1], [0,1,1,2], [0,2,1, 3], [0,3,1,4], [0,4,1,5], [0,5,1,6], [0,6,1,7], [0,7,1, 8], [0,8,1,9], [0,9,1,10], [0,10,1,11], [0,11,1,12], [0,12,1, 13], [0,13,1,14], ..., [0,9998,1,9999]].

We will combine these improvements with the previous solution, bring it in full, with some improvements:

 treechk(X,[],t([],X,[])). treechk([X1,Y1,X2,Y2],t(L,[X1,Y11,X2,Y22],R),t(L,[X1,Yr,X2,Yr2],R)):- (Y1=Y22;Y2=Y11),!,Yr is min(Y1,Y11),Yr2 is max(Y2,Y22). %union treechk(X,t(L,Root,R),t(L,Root,NewR)):- righter(X,Root),!,treechk(X,R,NewR). treechk(X,t(L,Root,R),t(NewL,Root,R)):- not(cross(X,Root)),treechk(X,L,NewL). righter([X1,_,_,_],[_,_,X2,_]):-X1>X2. findsum([],Sres,Sres,LConerRes,LConerRes,RConerRes,RConerRes,_). findsum([[Lx,Ly,Rx,Ry]|T],Scur,Sres,LConerCur,LConerRes,RConerCur,RConerRes,RectTree):- coner(Lx:Ly,LConerCur,=<,LConerCur2), coner(Rx:Ry,RConerCur,>=,RConerCur2), Scur2 is Scur+abs(Rx-Lx)*abs(Ry-Ly), treechk([Lx,Ly,Rx,Ry],RectTree,RectTree2),!, findsum(T,Scur2,Sres,LConerCur2,LConerRes,RConerCur2,RConerRes,RectTree2). isRectangleCover(Rects):- [[Lx,Ly,Rx,Ry]|_]=Rects, findsum(Rects,0,S,Lx:Ly,LconerX:LconerY,Rx:Ry,RconerX:RconerY,[]),!, S=:= abs(RconerX-LconerX)*abs(RconerY-LconerY). coner(X1:Y1,X2:Y2,Dir,X1:Y1):-apply(Dir,[X1,X2]),apply(Dir,[Y1,Y2]),!. coner(_,XY,_,XY). cross(X,X):-!. cross(X,Y):-cross2(X,Y),!. cross(X,Y):-cross2(Y,X). cross2([X11,Y11,X12,Y12],[_,_,X22,Y22]):-X11<X22,X22=<X12, Y11<Y22,Y22=<Y12,!. %right-top cross2([X11,Y11,X12,Y12],[X21,_,_,Y22]):-X11=<X21,X21<X12, Y11<Y22,Y22=<Y12,!. %left-top cross2([X11,Y11,X12,Y12],[_,Y21,X22,_]):-X11<X22,X22=<X12, Y11=<Y21,Y21<Y12,!. %right-bottom cross2([X11,Y11,X12,Y12],[X21,Y21,_,_]):-X11=<X21,X21<X12, Y11=<Y21,Y21<Y12. %left-bottom 

Here is the time to perform the "heavy" tests:

 goal-true->ok:0/sec 41:length=10000 goal-true->ok:0/sec 42:length=3982 goal-true->ok:0/sec 43:length=10222 goal-true->ok:2/sec 44:length=10779 goal-false->ok:1/sec 45:length=11000 goal-true->ok:1/sec 

At this improvement I will finish, all tests pass correctly, time is satisfactory. Who is interested, I suggest to try online or here .

Total

Articles related to functional programming, with a constant frequency found on the portal. I mention another aspect of the declarative approach - logical programming. You can represent tasks using a logical description, there are facts and rules, assumptions and effects, relationships and recursive relationships. The task description should be turned into a set of relations describing it. The result is a consequence of decomposing the problem into simpler components.

A program in a declarative language can be used as a set of statements that should construct a result, solving a problem in its successful formulation. And the optimization may consist, for example, in the fact that a “cursory” description of the method for controlling the intersections of rectangles may require clarification, it is possible to construct a tree structure for more efficient calculations.

And ... Prolog from the source code styles disappeared somewhere, half a year ago I used it. I had to specify the "related" Erlang. But doesn’t it look like “popularity”? Fortran and BASIC are not in the list, what is the language rating?