Craftsman Newton's Cradle
Hello, dear reader! I already wrote the first article with the very basics of Box2D in Eclipse in Java. Today, using the example of Newton's Cradle, I will show you how to set up the connection of objects in this wonderful physical library.
What do we expect to see?

Figure 1. Too good!
Definitely something absolutely different from that!
')
For the libGDX connection , see the first article.
The composition of the project has not changed:
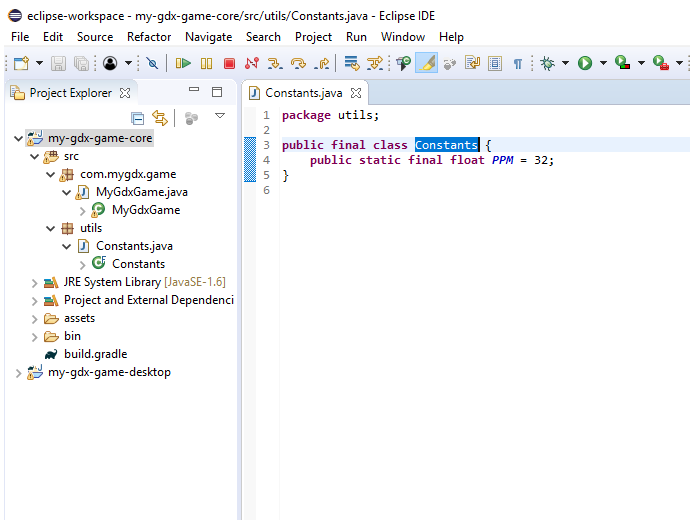
Figure 2. The project. Folders and packages.
I added the Utils package to the Core folder with the class Constants, which contains only one constant - the number of pixels per meter. This is so that the world is not gigantic.
Here is the code for the DesktopLauncher class from the com.mygdx.game.desktop package:
In our physical model, the coefficient of elasticity will be of paramount importance. The higher it is, the more vibrations the pendulum will make. In Box2D, the restitution parameter for FixtureDef can take values from 0 to 1.0f, where 0 is absolutely not an elastic body, and 1.0f is absolutely elastic. The best model of Newton's Cradle I did when restitution = 0.8f:
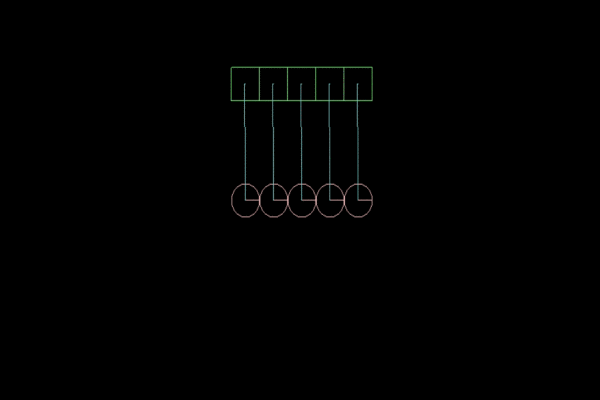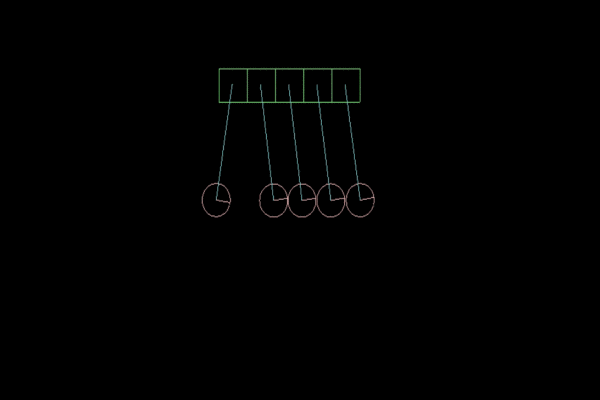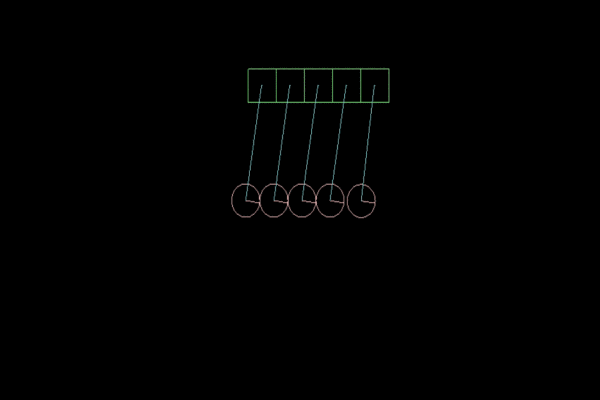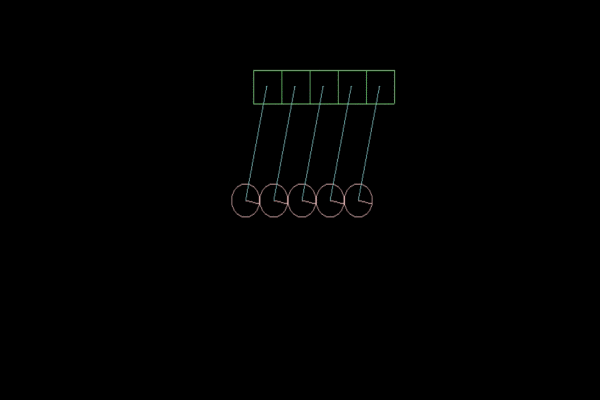
Figure 3 . Coefficient of elasticity = 0.8f, for greater clarity, slow motion.
You can independently change the coefficients and get different results. In addition, textures can be applied to primitives to achieve greater realism.
Next will be presented gif-images for different values of the coefficient of elasticity.
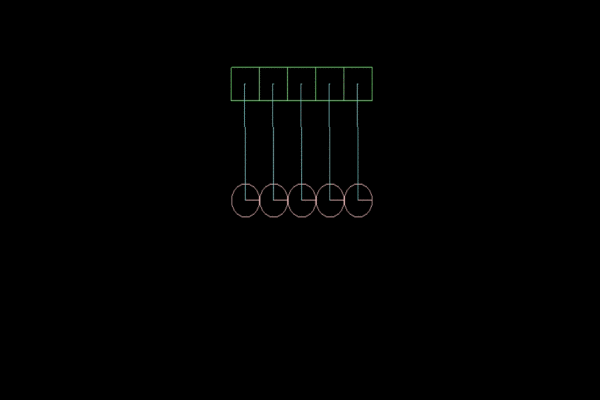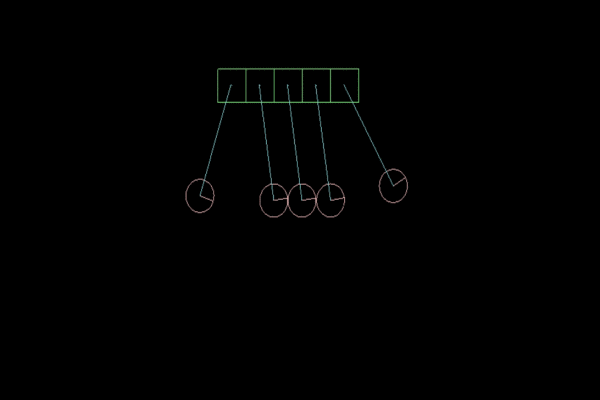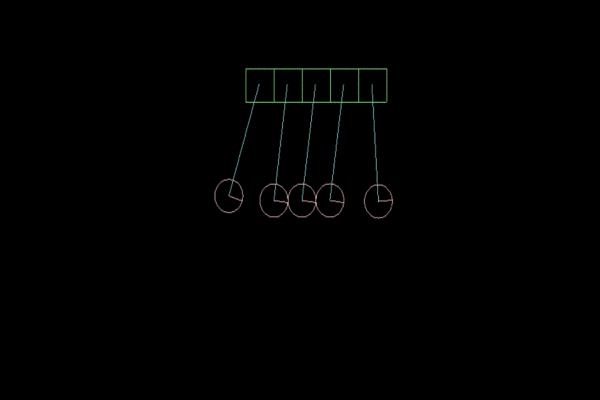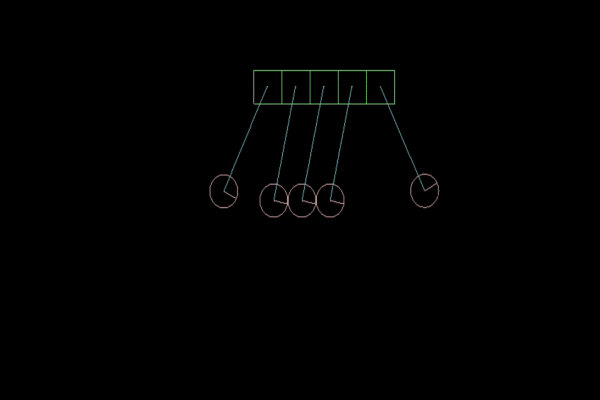
Figure 4. Elasticity factor of 1f.

Figure 5. Elasticity factor of 0.5f.

Figure 6. Elasticity factor of 0.2f.

Figure 7. Elasticity factor of 0.
A lot of ideas, I try to spread the results as much as possible! Thank you for reading to the end, I hope the article was useful for you! Let's make real chaos together in the game world thanks to the Box2D library!
PS I will answer all questions in the comments.
What do we expect to see?

Figure 1. Too good!
Definitely something absolutely different from that!
')
For the libGDX connection , see the first article.
The composition of the project has not changed:

Figure 2. The project. Folders and packages.
I added the Utils package to the Core folder with the class Constants, which contains only one constant - the number of pixels per meter. This is so that the world is not gigantic.
Here is the code for the DesktopLauncher class from the com.mygdx.game.desktop package:
Paste this code into the class and forget about it.
package com.mygdx.game.desktop; import com.badlogic.gdx.backends.lwjgl.LwjglApplication; import com.badlogic.gdx.backends.lwjgl.LwjglApplicationConfiguration; import com.mygdx.game.MyGdxGame; public class DesktopLauncher { public static void main(String[] arg) { LwjglApplicationConfiguration config = new LwjglApplicationConfiguration(); // config.width = 720; // config.height = 480; config.backgroundFPS = 60; config.foregroundFPS = 60; new LwjglApplication(new MyGdxGame(), config); } } In our physical model, the coefficient of elasticity will be of paramount importance. The higher it is, the more vibrations the pendulum will make. In Box2D, the restitution parameter for FixtureDef can take values from 0 to 1.0f, where 0 is absolutely not an elastic body, and 1.0f is absolutely elastic. The best model of Newton's Cradle I did when restitution = 0.8f:

Figure 3 . Coefficient of elasticity = 0.8f, for greater clarity, slow motion.
Implementation code:
package com.mygdx.game; import com.badlogic.gdx.ApplicationAdapter; import com.badlogic.gdx.Gdx; import com.badlogic.gdx.Input.Keys; import com.badlogic.gdx.graphics.GL20; import com.badlogic.gdx.graphics.OrthographicCamera; import com.badlogic.gdx.math.Vector2; import com.badlogic.gdx.math.Vector3; import com.badlogic.gdx.physics.box2d.Body; import com.badlogic.gdx.physics.box2d.BodyDef; import com.badlogic.gdx.physics.box2d.Box2DDebugRenderer; import com.badlogic.gdx.physics.box2d.CircleShape; import com.badlogic.gdx.physics.box2d.FixtureDef; import com.badlogic.gdx.physics.box2d.PolygonShape; import com.badlogic.gdx.physics.box2d.World; import com.badlogic.gdx.physics.box2d.joints.RevoluteJointDef; import utils.Constants; public class MyGdxGame extends ApplicationAdapter { private OrthographicCamera camera; private boolean DEBUG = false; private World world; private Body plos; private Body plos2; private Body plos3; private Body plos1; private Body plos4; private Box2DDebugRenderer b2dr; private Body ball; private Body ball1; private Body ball2; private Body ball3; private Body ball4; public void create() { float w = Gdx.graphics.getWidth(); float h = Gdx.graphics.getHeight(); camera = new OrthographicCamera(); camera.setToOrtho(false, w / 2, h / 2); world = new World(new Vector2(0, -9.8f), false); b2dr = new Box2DDebugRenderer(); // plos = createplos(20 / Constants.PPM); plos1 = createplos(0 / Constants.PPM); plos2 = createplos(40 / Constants.PPM); plos3 = createplos(80 / Constants.PPM); plos4 = createplos(60 / Constants.PPM); // ball = createball(20 / Constants.PPM); ball1 = createball(40 / Constants.PPM); ball2 = createball(60 / Constants.PPM); ball3 = createball(0 / Constants.PPM); ball4 = createball(80 / Constants.PPM); // rotation(plos, ball); rotation(plos2, ball1); rotation(plos1, ball3); rotation(plos4, ball2); rotation(plos3, ball4); } // public void rotation(Body body1, Body body2) { RevoluteJointDef rjd = new RevoluteJointDef(); rjd.bodyA = body1; rjd.bodyB = body2; rjd.collideConnected = false; // rjd.localAnchorB.set((plos.getPosition().x) / Constants.PPM, plos.getPosition().y / Constants.PPM + 2); // rjd.localAnchorA.set((plos.getPosition().y - 6.8f) / Constants.PPM, plos.getPosition().x / Constants.PPM); world.createJoint(rjd); } public void render() { update(Gdx.graphics.getDeltaTime()); Gdx.gl.glClearColor(0, 0, 0, 1); Gdx.gl.glClear(GL20.GL_COLOR_BUFFER_BIT); b2dr.render(world, camera.combined.scl(Constants.PPM)); } public void resize(int width, int height) { camera.setToOrtho(false, width / 2, height / 2); } public void dispose() { world.dispose(); b2dr.dispose(); } public void update(float delta) { world.step(1 / 60f, 6, 2); cameraUpdate(delta); inputUpdate(delta); } public void inputUpdate(float delta) { // , -7 / x, -7 / y if (Gdx.input.isKeyPressed(Keys.SPACE)) { ball3.setLinearVelocity(-7, -7); } } // public void cameraUpdate(float delta) { Vector3 position = camera.position; position.x = ball1.getPosition().x * Constants.PPM; position.y = ball1.getPosition().y * Constants.PPM; camera.position.set(position); camera.update(); } // public Body createplos(float xo) { PolygonShape shape = new PolygonShape(); Body fBody; BodyDef def = new BodyDef(); def.type = BodyDef.BodyType.StaticBody; def.position.set(xo, 200 / Constants.PPM); def.fixedRotation = true; fBody = world.createBody(def); shape.setAsBox(10 / Constants.PPM, 10 / Constants.PPM); fBody.createFixture(shape, 0.001f); shape.dispose(); return fBody; } // public Body createball(float xo) { Body pBody; BodyDef def = new BodyDef(); def.type = BodyDef.BodyType.DynamicBody; def.position.set(xo, 100 / Constants.PPM); def.fixedRotation = false; pBody = world.createBody(def); CircleShape shape = new CircleShape(); shape.setRadius(10 / Constants.PPM); pBody.createFixture(shape, 0.0001f); def.bullet = true; FixtureDef fd = new FixtureDef(); // fd.restitution = 0.8f; // fd.density = 10.0f; // fd.friction = 0f; fd.shape = shape; pBody.createFixture(fd); shape.dispose(); return pBody; } } You can independently change the coefficients and get different results. In addition, textures can be applied to primitives to achieve greater realism.
Next will be presented gif-images for different values of the coefficient of elasticity.

Figure 4. Elasticity factor of 1f.

Figure 5. Elasticity factor of 0.5f.

Figure 6. Elasticity factor of 0.2f.

Figure 7. Elasticity factor of 0.
A lot of ideas, I try to spread the results as much as possible! Thank you for reading to the end, I hope the article was useful for you! Let's make real chaos together in the game world thanks to the Box2D library!
PS I will answer all questions in the comments.
Source: https://habr.com/ru/post/450346/
All Articles