How the rendering of The Witcher 3 is implemented: lightning, witches sneak and other effects

Part 1. Lightning
In this part we will look at the lightning rendering process in Witcher 3: Wild Hunt.
Lightning rendering is done a little after the rain curtain effect, but it still happens in the direct rendering pass. Lightning can be seen on this video:
They disappear very quickly, so it's best to watch videos at 0.25 speed.
')
You can see that these are not static images; over time, their brightness varies slightly.
From the point of view of the nuances of rendering, there are a lot of similarities with drawing a curtain of rain in the distance, for example, the same blending state (additive blending) and depth (checking is on, no depth recording is performed).

Scene without lightning

Scene with lightning
From the point of view of lightning geometry in The Witcher 3, these are tree-like meshes. This example of lightning is represented by the following mesh:

It has UV coordinates and normal vectors. All this is useful at the vertex shader stage.
Vertex shader
Let's take a look at the vertex shader assembler code:
vs_5_0 dcl_globalFlags refactoringAllowed dcl_constantbuffer cb1[9], immediateIndexed dcl_constantbuffer cb2[6], immediateIndexed dcl_input v0.xyz dcl_input v1.xy dcl_input v2.xyz dcl_input v4.xyzw dcl_input v5.xyzw dcl_input v6.xyzw dcl_input v7.xyzw dcl_output o0.xy dcl_output o1.xyzw dcl_output_siv o2.xyzw, position dcl_temps 3 0: mov o0.xy, v1.xyxx 1: mov o1.xyzw, v7.xyzw 2: mul r0.xyzw, v5.xyzw, cb1[0].yyyy 3: mad r0.xyzw, v4.xyzw, cb1[0].xxxx, r0.xyzw 4: mad r0.xyzw, v6.xyzw, cb1[0].zzzz, r0.xyzw 5: mad r0.xyzw, cb1[0].wwww, l(0.000000, 0.000000, 0.000000, 1.000000), r0.xyzw 6: mov r1.w, l(1.000000) 7: mad r1.xyz, v0.xyzx, cb2[4].xyzx, cb2[5].xyzx 8: dp4 r2.x, r1.xyzw, v4.xyzw 9: dp4 r2.y, r1.xyzw, v5.xyzw 10: dp4 r2.z, r1.xyzw, v6.xyzw 11: add r2.xyz, r2.xyzx, -cb1[8].xyzx 12: dp3 r1.w, r2.xyzx, r2.xyzx 13: rsq r1.w, r1.w 14: div r1.w, l(1.000000, 1.000000, 1.000000, 1.000000), r1.w 15: mul r1.w, r1.w, l(0.000001) 16: mad r2.xyz, v2.xyzx, l(2.000000, 2.000000, 2.000000, 0.000000), l(-1.000000, -1.000000, -1.000000, 0.000000) 17: mad r1.xyz, r2.xyzx, r1.wwww, r1.xyzx 18: mov r1.w, l(1.000000) 19: dp4 o2.x, r1.xyzw, r0.xyzw 20: mul r0.xyzw, v5.xyzw, cb1[1].yyyy 21: mad r0.xyzw, v4.xyzw, cb1[1].xxxx, r0.xyzw 22: mad r0.xyzw, v6.xyzw, cb1[1].zzzz, r0.xyzw 23: mad r0.xyzw, cb1[1].wwww, l(0.000000, 0.000000, 0.000000, 1.000000), r0.xyzw 24: dp4 o2.y, r1.xyzw, r0.xyzw 25: mul r0.xyzw, v5.xyzw, cb1[2].yyyy 26: mad r0.xyzw, v4.xyzw, cb1[2].xxxx, r0.xyzw 27: mad r0.xyzw, v6.xyzw, cb1[2].zzzz, r0.xyzw 28: mad r0.xyzw, cb1[2].wwww, l(0.000000, 0.000000, 0.000000, 1.000000), r0.xyzw 29: dp4 o2.z, r1.xyzw, r0.xyzw 30: mul r0.xyzw, v5.xyzw, cb1[3].yyyy 31: mad r0.xyzw, v4.xyzw, cb1[3].xxxx, r0.xyzw 32: mad r0.xyzw, v6.xyzw, cb1[3].zzzz, r0.xyzw 33: mad r0.xyzw, cb1[3].wwww, l(0.000000, 0.000000, 0.000000, 1.000000), r0.xyzw 34: dp4 o2.w, r1.xyzw, r0.xyzw 35: ret There are many similarities with the rain shade vertex shader, so I will not repeat. I want to show you the important difference that is in lines 11-18:
11: add r2.xyz, r2.xyzx, -cb1[8].xyzx 12: dp3 r1.w, r2.xyzx, r2.xyzx 13: rsq r1.w, r1.w 14: div r1.w, l(1.000000, 1.000000, 1.000000, 1.000000), r1.w 15: mul r1.w, r1.w, l(0.000001) 16: mad r2.xyz, v2.xyzx, l(2.000000, 2.000000, 2.000000, 0.000000), l(-1.000000, -1.000000, -1.000000, 0.000000) 17: mad r1.xyz, r2.xyzx, r1.wwww, r1.xyzx 18: mov r1.w, l(1.000000) 19: dp4 o2.x, r1.xyzw, r0.xyzw First, cb1 [8] .xyz is the position of the camera, and r2.xyz is the position in world space, that is, line 11 calculates the vector from the camera to the position in the world. Then lines 12-15 calculate length (worldPos - cameraPos) * 0.000001.
v2.xyz is the normal vector of the incoming geometry. Line 16 extends it from interval [0-1] to interval [-1; 1].
Then the final position in the world is calculated:
finalWorldPos = worldPos + length (worldPos - cameraPos) * 0.000001 * normalVector
The HLSL code snippet for this operation will be something like this:
... // final world-space position float3 vNormal = Input.NormalW * 2.0 - 1.0; float lencameratoworld = length( PositionL - g_cameraPos.xyz) * 0.000001; PositionL += vNormal*lencameratoworld; // SV_Posiiton float4x4 matModelViewProjection = mul(g_viewProjMatrix, matInstanceWorld ); Output.PositionH = mul( float4(PositionL, 1.0), transpose(matModelViewProjection) ); return Output; This operation results in a small “explosion” of the mesh (in the direction of the normal vector). I experimented by replacing 0.000001 with several other values. Here are the results:

0.000002

0.000005

0.00001

0.000025
Pixel shader
Great, we figured out a vertex shader, now it's time to take on the assembler code of the pixel shader!
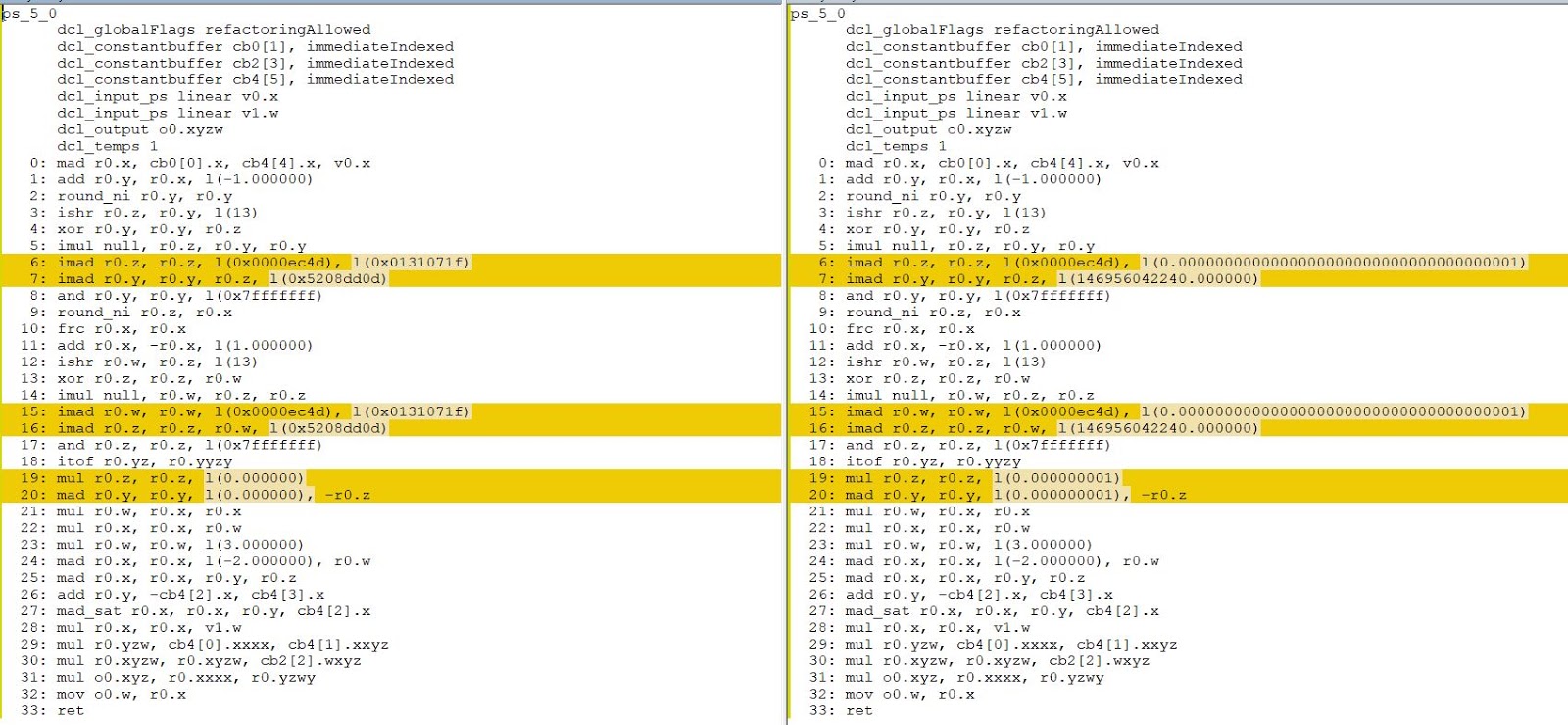
ps_5_0 dcl_globalFlags refactoringAllowed dcl_constantbuffer cb0[1], immediateIndexed dcl_constantbuffer cb2[3], immediateIndexed dcl_constantbuffer cb4[5], immediateIndexed dcl_input_ps linear v0.x dcl_input_ps linear v1.w dcl_output o0.xyzw dcl_temps 1 0: mad r0.x, cb0[0].x, cb4[4].x, v0.x 1: add r0.y, r0.x, l(-1.000000) 2: round_ni r0.y, r0.y 3: ishr r0.z, r0.y, l(13) 4: xor r0.y, r0.y, r0.z 5: imul null, r0.z, r0.y, r0.y 6: imad r0.z, r0.z, l(0x0000ec4d), l(0.0000000000000000000000000000000000001) 7: imad r0.y, r0.y, r0.z, l(146956042240.000000) 8: and r0.y, r0.y, l(0x7fffffff) 9: round_ni r0.z, r0.x 10: frc r0.x, r0.x 11: add r0.x, -r0.x, l(1.000000) 12: ishr r0.w, r0.z, l(13) 13: xor r0.z, r0.z, r0.w 14: imul null, r0.w, r0.z, r0.z 15: imad r0.w, r0.w, l(0x0000ec4d), l(0.0000000000000000000000000000000000001) 16: imad r0.z, r0.z, r0.w, l(146956042240.000000) 17: and r0.z, r0.z, l(0x7fffffff) 18: itof r0.yz, r0.yyzy 19: mul r0.z, r0.z, l(0.000000001) 20: mad r0.y, r0.y, l(0.000000001), -r0.z 21: mul r0.w, r0.x, r0.x 22: mul r0.x, r0.x, r0.w 23: mul r0.w, r0.w, l(3.000000) 24: mad r0.x, r0.x, l(-2.000000), r0.w 25: mad r0.x, r0.x, r0.y, r0.z 26: add r0.y, -cb4[2].x, cb4[3].x 27: mad_sat r0.x, r0.x, r0.y, cb4[2].x 28: mul r0.x, r0.x, v1.w 29: mul r0.yzw, cb4[0].xxxx, cb4[1].xxyz 30: mul r0.xyzw, r0.xyzw, cb2[2].wxyz 31: mul o0.xyz, r0.xxxx, r0.yzwy 32: mov o0.w, r0.x 33: ret Good news: the code is not so long.
Bad news:
3: ishr r0.z, r0.y, l(13) 4: xor r0.y, r0.y, r0.z 5: imul null, r0.z, r0.y, r0.y 6: imad r0.z, r0.z, l(0x0000ec4d), l(0.0000000000000000000000000000000000001) 7: imad r0.y, r0.y, r0.z, l(146956042240.000000) 8: and r0.y, r0.y, l(0x7fffffff) ... what is it all about?
Honestly, this is not the first time I have seen such a piece of ... assembly code in the Witcher 3 shaders. But when I met him for the first time, I thought: “What the hell is that?”
Something similar can be found in some other TW3 shaders. I will not describe my adventures with this fragment, and just say that the answer lies in the integer noise :
// For more details see: http://libnoise.sourceforge.net/noisegen/ float integerNoise( int n ) { n = (n >> 13) ^ n; int nn = (n * (n * n * 60493 + 19990303) + 1376312589) & 0x7fffffff; return ((float)nn / 1073741824.0); } As you can see, in the pixel shader, it is called twice. Using the guides from this website, we can understand how smooth noise is properly implemented. I'll come back to this in a minute.
Look at line 0 - here we perform the animation based on the following formula:
animation = elapsedTime * animationSpeed + TextureUV.x
These values, after rounding down ( floor ) (instruction round_ni ) in the future become input points for integer noise. We usually calculate the noise value for two integers, and then we calculate the final, interpolated value between them (see the libnoise website for details).
Well, okay, this is integer noise, but after all, all the previously mentioned values (also rounded down) are float!
Note that there are no ftoi instructions here . I assume that programmers from CD Projekt Red used the internal HLSL asint function here , which performs the “reinterpret_cast” conversion of floating-point values and processes them as an integer pattern.
The interpolation weight for two values is calculated in lines 10-11.
interpolationWeight = 1.0 - frac (animation);
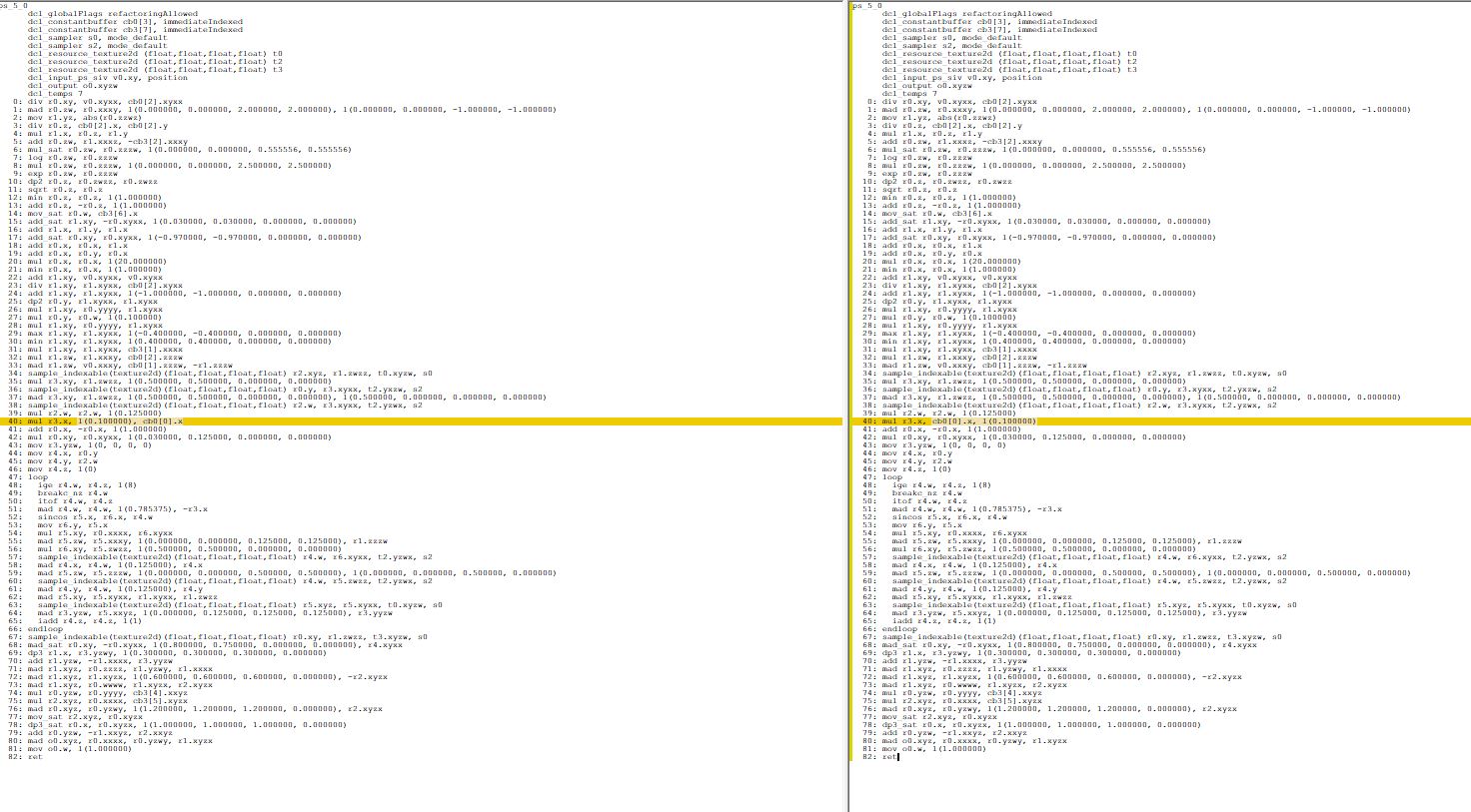
This approach allows us to perform interpolation between values over time.
To create smooth noise, this interpolator is passed to the SCurve function:
float s_curve( float x ) { float x2 = x * x; float x3 = x2 * x; // -2x^3 + 3x^2 return -2.0*x3 + 3.0*x2; } 
Smoothstep [libnoise.sourceforge.net] function
This feature is known as "smoothstep". But as can be seen from the assembler code, this is not the internal smoothstep function from HLSL. Internal function applies constraints so that values are correct. But since we know that interpolationWeight will always be in the interval [0-1], you can safely skip these checks.
When calculating the final value, several multiplication operations are used. See how the final alpha output can vary depending on the noise value. This is convenient because it will affect the opacity of the rendered lightning, just like in real life.
Ready pixel shader:
cbuffer cbPerFrame : register (b0) { float4 cb0_v0; float4 cb0_v1; float4 cb0_v2; float4 cb0_v3; } cbuffer cbPerFrame : register (b2) { float4 cb2_v0; float4 cb2_v1; float4 cb2_v2; float4 cb2_v3; } cbuffer cbPerFrame : register (b4) { float4 cb4_v0; float4 cb4_v1; float4 cb4_v2; float4 cb4_v3; float4 cb4_v4; } struct VS_OUTPUT { float2 Texcoords : Texcoord0; float4 InstanceLODParams : INSTANCE_LOD_PARAMS; float4 PositionH : SV_Position; }; // Shaders in TW3 use integer noise. // For more details see: http://libnoise.sourceforge.net/noisegen/ float integerNoise( int n ) { n = (n >> 13) ^ n; int nn = (n * (n * n * 60493 + 19990303) + 1376312589) & 0x7fffffff; return ((float)nn / 1073741824.0); } float s_curve( float x ) { float x2 = x * x; float x3 = x2 * x; // -2x^3 + 3x^2 return -2.0*x3 + 3.0*x2; } float4 Lightning_TW3_PS( in VS_OUTPUT Input ) : SV_Target { // * Inputs float elapsedTime = cb0_v0.x; float animationSpeed = cb4_v4.x; float minAmount = cb4_v2.x; float maxAmount = cb4_v3.x; float colorMultiplier = cb4_v0.x; float3 colorFilter = cb4_v1.xyz; float3 lightningColorRGB = cb2_v2.rgb; // Animation using time and X texcoord float animation = elapsedTime * animationSpeed + Input.Texcoords.x; // Input parameters for Integer Noise. // They are floored and please note there are using asint. // That might be an optimization to avoid "ftoi" instructions. int intX0 = asint( floor(animation) ); int intX1 = asint( floor(animation-1.0) ); float n0 = integerNoise( intX0 ); float n1 = integerNoise( intX1 ); // We interpolate "backwards" here. float weight = 1.0 - frac(animation); // Following the instructions from libnoise, we perform // smooth interpolation here with cubic s-curve function. float noise = lerp( n0, n1, s_curve(weight) ); // Make sure we are in [0.0 - 1.0] range. float lightningAmount = saturate( lerp(minAmount, maxAmount, noise) ); lightningAmount *= Input.InstanceLODParams.w; // 1.0 lightningAmount *= cb2_v2.w; // 1.0 // Calculate final lightning color float3 lightningColor = colorMultiplier * colorFilter; lightningColor *= lighntingColorRGB; float3 finalLightningColor = lightningColor * lightningAmount; return float4( finalLightningColor, lightningAmount ); } Summarize
In this section, I described a way to render lightning in The Witcher 3.
I am very pleased that the assembler code from my shader is the same as the original!
Part 2. Silly tricks with the sky
This part will be slightly different from the previous ones. In it, I want to show you some aspects of the Witcher 3 sky shaders.
Why “stupid tricks” and not the whole shader? Well, for a few reasons. First of all, the sky shader Witcher 3 is a rather complicated beast. The pixel shader from the 2015 version contains 267 lines of the assembler code, and the shader from the DLC “Blood and Wine” already contains 385 lines.
Moreover, they receive a lot of input data, which is not very conducive to reverse engineering of the full (and readable!) HLSL code.
Therefore, I decided to show only a part of these tricks from these shaders. If I find something new, I will add a post.
The differences between the 2015 version and the DLC (2016) are very noticeable. In particular, they include differences in the calculation of stars and their flickering, a different approach to rendering the Sun ... The Shader "Blood and Wine" even calculates the Milky Way at night.
I'll start with the basics, and then talk about the stupid tricks.
The basics
As in most modern games, skydome is used to simulate the sky in Witcher 3. Look at the hemisphere that was used for this in Witcher 3 (2015). Note: in this case, the bounding box of this mesh is in the range from [0,0,0] to [1,1,1] (Z is the axis directed upwards) and has smoothly distributed UV. Later we use them.
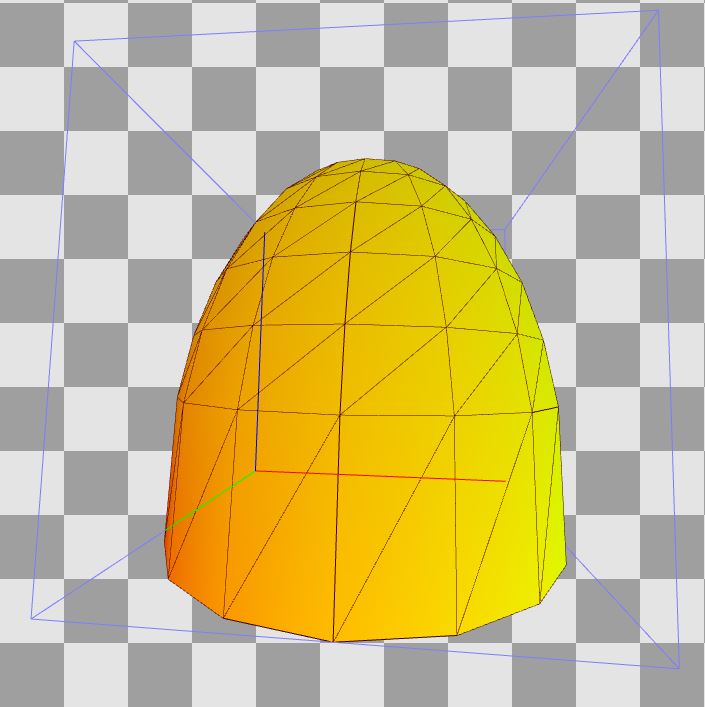
The idea behind the skydome is similar to the skybox idea (the only difference is in the mesh used). At the vertex shader stage, we transform the skydome relative to the observer (usually according to the camera position), which creates the illusion that the sky is really very far away - we will never get to it.
If you read the previous parts of this series of articles, then you know that the Witcher 3 uses the inverse depth, that is, the far plane has a value of 0.0f, and the near plane - 1.0f. To display the skydome entirely on the far plane, in the parameters of the overview window we set MinDepth to the same value as MaxDepth :

To find out how the MinDepth and MaxDepth fields are used during the conversion of the overview window, click here (docs.microsoft.com).
Vertex shader
Let's start with the vertex shader. In Witcher 3 (2015), the assembler shader code looks like this:
vs_5_0 dcl_globalFlags refactoringAllowed dcl_constantbuffer cb1[4], immediateIndexed dcl_constantbuffer cb2[6], immediateIndexed dcl_input v0.xyz dcl_input v1.xy dcl_output o0.xy dcl_output o1.xyz dcl_output_siv o2.xyzw, position dcl_temps 2 0: mov o0.xy, v1.xyxx 1: mad r0.xyz, v0.xyzx, cb2[4].xyzx, cb2[5].xyzx 2: mov r0.w, l(1.000000) 3: dp4 o1.x, r0.xyzw, cb2[0].xyzw 4: dp4 o1.y, r0.xyzw, cb2[1].xyzw 5: dp4 o1.z, r0.xyzw, cb2[2].xyzw 6: mul r1.xyzw, cb1[0].yyyy, cb2[1].xyzw 7: mad r1.xyzw, cb2[0].xyzw, cb1[0].xxxx, r1.xyzw 8: mad r1.xyzw, cb2[2].xyzw, cb1[0].zzzz, r1.xyzw 9: mad r1.xyzw, cb1[0].wwww, l(0.000000, 0.000000, 0.000000, 1.000000), r1.xyzw 10: dp4 o2.x, r0.xyzw, r1.xyzw 11: mul r1.xyzw, cb1[1].yyyy, cb2[1].xyzw 12: mad r1.xyzw, cb2[0].xyzw, cb1[1].xxxx, r1.xyzw 13: mad r1.xyzw, cb2[2].xyzw, cb1[1].zzzz, r1.xyzw 14: mad r1.xyzw, cb1[1].wwww, l(0.000000, 0.000000, 0.000000, 1.000000), r1.xyzw 15: dp4 o2.y, r0.xyzw, r1.xyzw 16: mul r1.xyzw, cb1[2].yyyy, cb2[1].xyzw 17: mad r1.xyzw, cb2[0].xyzw, cb1[2].xxxx, r1.xyzw 18: mad r1.xyzw, cb2[2].xyzw, cb1[2].zzzz, r1.xyzw 19: mad r1.xyzw, cb1[2].wwww, l(0.000000, 0.000000, 0.000000, 1.000000), r1.xyzw 20: dp4 o2.z, r0.xyzw, r1.xyzw 21: mul r1.xyzw, cb1[3].yyyy, cb2[1].xyzw 22: mad r1.xyzw, cb2[0].xyzw, cb1[3].xxxx, r1.xyzw 23: mad r1.xyzw, cb2[2].xyzw, cb1[3].zzzz, r1.xyzw 24: mad r1.xyzw, cb1[3].wwww, l(0.000000, 0.000000, 0.000000, 1.000000), r1.xyzw 25: dp4 o2.w, r0.xyzw, r1.xyzw 26: ret In this case, the vertex shader transmits only texcoords and position in world space to the output. In Blood and Wine, he also derives the normalized normal vector. I will consider the 2015 version because it is simpler.
Look at the constant buffer, denoted as cb2 :
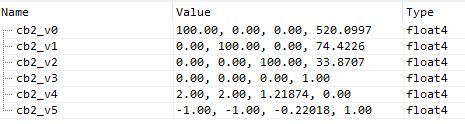
Here we have the world matrix (uniform scaling by 100 and translation relative to the camera position). Nothing complicated. cb2_v4 and cb2_v5 are scale / deviation coefficients used to convert vertex positions from interval [0-1] to interval [-1; 1]. But here these coefficients “compress” the Z axis (upward).

In the previous parts of the series, we had similar vertex shaders. The general algorithm is to transfer texcoords further, then the Position is calculated taking into account scale / deviation factors, then PositionW is calculated in world space, then the final position of the clipping space is calculated by multiplying matWorld and matViewProj matrices -> their product is used to multiply by Position to get the final SV_Position .
Therefore, the HLSL of this vertex shader should be something like this:
struct InputStruct { float3 param0 : POSITION; float2 param1 : TEXCOORD; float3 param2 : NORMAL; float4 param3 : TANGENT; }; struct OutputStruct { float2 param0 : TEXCOORD0; float3 param1 : TEXCOORD1; float4 param2 : SV_Position; }; OutputStruct EditedShaderVS(in InputStruct IN) { OutputStruct OUT = (OutputStruct)0; // Simple texcoords passing OUT.param0 = IN.param1; // * Manually construct world and viewProj martices from float4s: row_major matrix matWorld = matrix(cb2_v0, cb2_v1, cb2_v2, float4(0,0,0,1) ); matrix matViewProj = matrix(cb1_v0, cb1_v1, cb1_v2, cb1_v3); // * Some optional fun with worldMatrix // a) Scale //matWorld._11 = matWorld._22 = matWorld._33 = 0.225f; // b) Translate // XYZ //matWorld._14 = 520.0997; //matWorld._24 = 74.4226; //matWorld._34 = 113.9; // Local space - note the scale+bias here! //float3 meshScale = float3(2.0, 2.0, 2.0); //float3 meshBias = float3(-1.0, -1.0, -0.4); float3 meshScale = cb2_v4.xyz; float3 meshBias = cb2_v5.xyz; float3 Position = IN.param0 * meshScale + meshBias; // World space float4 PositionW = mul(float4(Position, 1.0), transpose(matWorld) ); OUT.param1 = PositionW.xyz; // Clip space - original approach from The Witcher 3 matrix matWorldViewProj = mul(matViewProj, matWorld); OUT.param2 = mul( float4(Position, 1.0), transpose(matWorldViewProj) ); return OUT; } Comparison of my shader (left) and original (right):

A great feature of RenderDoc is that it allows us to perform an injection of our own shader instead of the original one, and these changes will affect the pipeline to the very end of the frame. As you can see from the HLSL code, I have provided several options for zooming and transforming the final geometry. You can experiment with them and get very funny results:

Vertex Shader Optimization
Have you noticed the problem of the original vertex shader? The matrix multiplication per matrix is completely redundant! I found this in at least a few vertex shaders (for example, in a shader a rain curtain in the distance ). We can optimize it by immediately multiplying PositionW by matViewProj !
So, we can replace this code with HLSL:
// Clip space - original approach from The Witcher 3 matrix matWorldViewProj = mul(matViewProj, matWorld); OUT.param2 = mul( float4(Position, 1.0), transpose(matWorldViewProj) ); as follows:
// Clip space - optimized version OUT.param2 = mul( matViewProj, PositionW ); The optimized version gives us the following assembly code:
vs_5_0 dcl_globalFlags refactoringAllowed dcl_constantbuffer CB1[4], immediateIndexed dcl_constantbuffer CB2[6], immediateIndexed dcl_input v0.xyz dcl_input v1.xy dcl_output o0.xy dcl_output o1.xyz dcl_output_siv o2.xyzw, position dcl_temps 2 0: mov o0.xy, v1.xyxx 1: mad r0.xyz, v0.xyzx, cb2[4].xyzx, cb2[5].xyzx 2: mov r0.w, l(1.000000) 3: dp4 r1.x, r0.xyzw, cb2[0].xyzw 4: dp4 r1.y, r0.xyzw, cb2[1].xyzw 5: dp4 r1.z, r0.xyzw, cb2[2].xyzw 6: mov o1.xyz, r1.xyzx 7: mov r1.w, l(1.000000) 8: dp4 o2.x, cb1[0].xyzw, r1.xyzw 9: dp4 o2.y, cb1[1].xyzw, r1.xyzw 10: dp4 o2.z, cb1[2].xyzw, r1.xyzw 11: dp4 o2.w, cb1[3].xyzw, r1.xyzw 12: ret As you can see, we reduced the number of instructions from 26 to 12 — a rather significant change. I do not know how widespread this problem is in the game, but for God's sake, CD Projekt Red, maybe release a patch? :)
And I'm not joking. You can insert my optimized shader instead of the original RenderDoc and you will see that this optimization does not affect anything visually. Honestly, I don’t understand why CD Projekt Red decided to perform full matrix multiplication by a matrix ...
The sun
In The Witcher 3 (2015), the calculation of atmospheric scattering and the Sun consists of two separate rendering calls:

Witcher 3 (2015) - to

Witcher 3 (2015) - with the sky

Witcher 3 (2015) - with the sky + Sun
Rendering the Sun in the 2015 version is very similar to rendering the Moon in terms of geometry and blending / depth states.
On the other hand, in “Blood and Wine” the sky with the Sun are rendered in one pass:

The Witcher 3: Blood and Wine (2016) - to the sky

The Witcher 3: Blood and Wine (2016) - with the sky and the Sun
No matter how you render the Sun, at some stage you will still need the (normalized) direction of the sunlight. The most logical way to get this vector is to use spherical coordinates . In fact, we need only two values that represent two angles (in radians!): Phi and theta . Having received them, we can assume that r = 1 , thus reducing it. Then for Cartesian coordinates with an upward Y-axis, you can write the following code in HLSL:
float3 vSunDir; vSunDir.x = sin(fTheta)*cos(fPhi); vSunDir.y = sin(fTheta)*sin(fPhi); vSunDir.z = cos(fTheta); vSunDir = normalize(vSunDir); Usually the direction of sunlight is calculated in the application, and then transferred to the buffer constants for further use.
Having received the direction of sunlight, we can delve into the assembler code of the “Blood and Wine” pixel shader ...
... 100: add r1.xyw, -r0.xyxz, cb12[0].xyxz 101: dp3 r2.x, r1.xywx, r1.xywx 102: rsq r2.x, r2.x 103: mul r1.xyw, r1.xyxw, r2.xxxx 104: mov_sat r2.xy, cb12[205].yxyy 105: dp3 r2.z, -r1.xywx, -r1.xywx 106: rsq r2.z, r2.z 107: mul r1.xyw, -r1.xyxw, r2.zzzz ... So, firstly, cb12 [0] .xyz is the camera position, and in r0.xyz we store the vertex position (this is the output from the vertex shader). Therefore, line 100 computes the worldToCamera vector. But take a look at lines 105-107. We can write them as normalize (-worldToCamera) , that is, we compute the normalized vector cameraToWorld .
120: dp3_sat r1.x, cb12[203].yzwy, r1.xywx Then we compute the scalar product of the vectors cameraToWorld and sunDirection ! Remember that they must be normalized. We also saturate this full expression to limit it to the interval [0-1].
Fine! This dot product is stored in r1.x. Let's see where it applies next ...
152: log r1.x, r1.x 153: mul r1.x, r1.x, cb12[203].x 154: exp r1.x, r1.x 155: mul r1.x, r2.y, r1.x The trinity “log, mul, exp” is exponentiation. As you can see, we raise our cosine (the scalar product of normalized vectors) to some degree. You may ask why. So we can create a gradient that imitates the sun. (And line 155 affects the opacity of this gradient, so that we, for example, reset it to completely hide the Sun). Here are some examples:

exponent = 54

exponent = 2400
With this gradient, we use it to interpolate between skyColor and sunColor ! To avoid artifacts, you need to saturate the value in line 120.
It is worth noting that this trick can be used to simulate the crowns of the moon (at low exponent values). For this we need a vector moonDirection , which can easily be calculated using spherical coordinates.
Ready HLSL code may look like the following snippet:
float3 vCamToWorld = normalize( PosW – CameraPos ); float cosTheta = saturate( dot(vSunDir, vCamToWorld) ); float sunGradient = pow( cosTheta, sunExponent ); float3 color = lerp( skyColor, sunColor, sunGradient ); Movement of stars
If you make a time-lapse of the clear night sky Witcher 3, then you can see that the stars are not static - they move a little across the sky! I noticed this almost by accident and wanted to find out how it was implemented.
Let's start with the fact that the stars in Witcher 3 are represented as a cubic map of 1024x1024x6. If you think about it, you can understand that this is a very convenient solution that makes it easy to attach directions for sampling a cube map.
Let's consider the following assembly code:
159: add r1.xyz, -v1.xyzx, cb1[8].xyzx 160: dp3 r0.w, r1.xyzx, r1.xyzx 161: rsq r0.w, r0.w 162: mul r1.xyz, r0.wwww, r1.xyzx 163: mul r2.xyz, cb12[204].zwyz, l(0.000000, 0.000000, 1.000000, 0.000000) 164: mad r2.xyz, cb12[204].yzwy, l(0.000000, 1.000000, 0.000000, 0.000000), -r2.xyzx 165: mul r4.xyz, r2.xyzx, cb12[204].zwyz 166: mad r4.xyz, r2.zxyz, cb12[204].wyzw, -r4.xyzx 167: dp3 r4.x, r1.xyzx, r4.xyzx 168: dp2 r4.y, r1.xyxx, r2.yzyy 169: dp3 r4.z, r1.xyzx, cb12[204].yzwy 170: dp3 r0.w, r4.xyzx, r4.xyzx 171: rsq r0.w, r0.w 172: mul r2.xyz, r0.wwww, r4.xyzx 173: sample_indexable(texturecube)(float,float,float,float) r4.xyz, r2.xyzx, t0.xyzw, s0 To calculate the final sampling vector (line 173), we start by calculating the normalized vector worldToCamera (lines 159-162).
Then we compute two vector products (163-164, 165-166) with moonDirection , and later we calculate three scalar products to get the final vector of sampling. HLSL code:
float3 vWorldToCamera = normalize( g_CameraPos.xyz - Input.PositionW.xyz ); float3 vMoonDirection = cb12_v204.yzw; float3 vStarsSamplingDir = cross( vMoonDirection, float3(0, 0, 1) ); float3 vStarsSamplingDir2 = cross( vStarsSamplingDir, vMoonDirection ); float dirX = dot( vWorldToCamera, vStarsSamplingDir2 ); float dirY = dot( vWorldToCamera, vStarsSamplingDir ); float dirZ = dot( vWorldToCamera, vMoonDirection); float3 dirXYZ = normalize( float3(dirX, dirY, dirZ) ); float3 starsColor = texNightStars.Sample( samplerAnisoWrap, dirXYZ ).rgb; Note to myself: this is a very well thought out code, and I should explore it in more detail.
Note to readers: if you know more about this operation, then tell me!
Flickering stars
Another interesting trick that I would like to explore in more detail is the twinkling of stars.For example, if you wander around Novigrad in clear weather, you will notice that the stars twinkle.
I was curious how it was implemented. It turned out that the difference between the 2015 version and Blood and Wine is quite large. For simplicity, I will consider the 2015 version.
So, we start right after sampling starsColor from the previous section:
174: mul r0.w, v0.x, l(100.000000) 175: round_ni r1.w, r0.w 176: mad r2.w, v0.y, l(50.000000), cb0[0].x 177: round_ni r4.w, r2.w 178: bfrev r4.w, r4.w 179: iadd r5.x, r1.w, r4.w 180: ishr r5.y, r5.x, l(13) 181: xor r5.x, r5.x, r5.y 182: imul null, r5.y, r5.x, r5.x 183: imad r5.y, r5.y, l(0x0000ec4d), l(0.0000000000000000000000000000000000001) 184: imad r5.x, r5.x, r5.y, l(146956042240.000000) 185: and r5.x, r5.x, l(0x7fffffff) 186: itof r5.x, r5.x 187: mad r5.y, v0.x, l(100.000000), l(-1.000000) 188: round_ni r5.y, r5.y 189: iadd r4.w, r4.w, r5.y 190: ishr r5.z, r4.w, l(13) 191: xor r4.w, r4.w, r5.z 192: imul null, r5.z, r4.w, r4.w 193: imad r5.z, r5.z, l(0x0000ec4d), l(0.0000000000000000000000000000000000001) 194: imad r4.w, r4.w, r5.z, l(146956042240.000000) 195: and r4.w, r4.w, l(0x7fffffff) 196: itof r4.w, r4.w 197: add r5.z, r2.w, l(-1.000000) 198: round_ni r5.z, r5.z 199: bfrev r5.z, r5.z 200: iadd r1.w, r1.w, r5.z 201: ishr r5.w, r1.w, l(13) 202: xor r1.w, r1.w, r5.w 203: imul null, r5.w, r1.w, r1.w 204: imad r5.w, r5.w, l(0x0000ec4d), l(0.0000000000000000000000000000000000001) 205: imad r1.w, r1.w, r5.w, l(146956042240.000000) 206: and r1.w, r1.w, l(0x7fffffff) 207: itof r1.w, r1.w 208: mul r1.w, r1.w, l(0.000000001) 209: iadd r5.y, r5.z, r5.y 210: ishr r5.z, r5.y, l(13) 211: xor r5.y, r5.y, r5.z 212: imul null, r5.z, r5.y, r5.y 213: imad r5.z, r5.z, l(0x0000ec4d), l(0.0000000000000000000000000000000000001) 214: imad r5.y, r5.y, r5.z, l(146956042240.000000) 215: and r5.y, r5.y, l(0x7fffffff) 216: itof r5.y, r5.y 217: frc r0.w, r0.w 218: add r0.w, -r0.w, l(1.000000) 219: mul r5.z, r0.w, r0.w 220: mul r0.w, r0.w, r5.z 221: mul r5.xz, r5.xxzx, l(0.000000001, 0.000000, 3.000000, 0.000000) 222: mad r0.w, r0.w, l(-2.000000), r5.z 223: frc r2.w, r2.w 224: add r2.w, -r2.w, l(1.000000) 225: mul r5.z, r2.w, r2.w 226: mul r2.w, r2.w, r5.z 227: mul r5.z, r5.z, l(3.000000) 228: mad r2.w, r2.w, l(-2.000000), r5.z 229: mad r4.w, r4.w, l(0.000000001), -r5.x 230: mad r4.w, r0.w, r4.w, r5.x 231: mad r5.x, r5.y, l(0.000000001), -r1.w 232: mad r0.w, r0.w, r5.x, r1.w 233: add r0.w, -r4.w, r0.w 234: mad r0.w, r2.w, r0.w, r4.w 235: mad r2.xyz, r0.wwww, l(0.000500, 0.000500, 0.000500, 0.000000), r2.xyzx 236: sample_indexable(texturecube)(float,float,float,float) r2.xyz, r2.xyzx, t0.xyzw, s0 237: log r4.xyz, r4.xyzx 238: mul r4.xyz, r4.xyzx, l(2.200000, 2.200000, 2.200000, 0.000000) 239: exp r4.xyz, r4.xyzx 240: log r2.xyz, r2.xyzx 241: mul r2.xyz, r2.xyzx, l(2.200000, 2.200000, 2.200000, 0.000000) 242: exp r2.xyz, r2.xyzx 243: mul r2.xyz, r2.xyzx, r4.xyzx HmLet's take a look at the end of this rather long assembly code.
After sampling starsColor in line 173, we calculate some offset value . This offset is used to distort the first direction of sampling (r2.xyz, line 235), and then again sample the cubic star map, perform gamma correction of these two values (237-242) and multiply them (243).
Simple, isn't it? Well, not quite. Let's think about this offset a bit . This value should be different throughout the skydome - equally twinkling stars would look very unrealistic.
To offsetwas as varied as possible, we use the fact that the UVs are stretched to skydome (v0.xy) and apply the elapsed time stored in the constant buffer (cb [0] .x).
If you are unfamiliar with these frightening ishr / xor / and, then in part about the effect of lightning, read about the integer noise.
As you can see, the integer noise is caused here four times, but it is different from the one used for lightning. To make the results even more random, the incoming integer for noise is the sum ( iadd ) and the bits are inverted with it (the internal function reversebits ; the bfrev instruction ).
So, now slow down. Let's start from the beginning.
We have 4 "iterations" of integer noise. I analyzed the assembler code, the calculations of all 4 iterations look like this:
int getInt( float x ) { return asint( floor(x) ); } int getReverseInt( float x ) { return reversebits( getInt(x) ); } // * Inputs - UV and elapsed time in seconds float2 starsUV; starsUV.x = 100.0 * Input.TextureUV.x; starsUV.y = 50.0 * Input.TextureUV.y + g_fTime; // * Iteration 1 int iStars1_A = getReverseInt( starsUV.y ); int iStars1_B = getInt( starsUV.x ); float fStarsNoise1 = integerNoise( iStars1_A + iStars1_B ); // * Iteration 2 int iStars2_A = getReverseInt( starsUV.y ); int iStars2_B = getInt( starsUV.x - 1.0 ); float fStarsNoise2 = integerNoise( iStars2_A + iStars2_B ); // * Iteration 3 int iStars3_A = getReverseInt( starsUV.y - 1.0 ); int iStars3_B = getInt( starsUV.x ); float fStarsNoise3 = integerNoise( iStars3_A + iStars3_B ); // * Iteration 4 int iStars4_A = getReverseInt( starsUV.y - 1.0 ); int iStars4_B = getInt( starsUV.x - 1.0 ); float fStarsNoise4 = integerNoise( iStars4_A + iStars4_B ); The final output of all 4 iterations (to find them, follow the itof instructions ):
Iteration 1 - r5.x,
Iteration 2 - r4.w,
Iteration 3 - r1.w,
Iteration 4 - r5.y
After the last itof (line 216 ) we have:
217: frc r0.w, r0.w 218: add r0.w, -r0.w, l(1.000000) 219: mul r5.z, r0.w, r0.w 220: mul r0.w, r0.w, r5.z 221: mul r5.xz, r5.xxzx, l(0.000000001, 0.000000, 3.000000, 0.000000) 222: mad r0.w, r0.w, l(-2.000000), r5.z 223: frc r2.w, r2.w 224: add r2.w, -r2.w, l(1.000000) 225: mul r5.z, r2.w, r2.w 226: mul r2.w, r2.w, r5.z 227: mul r5.z, r5.z, l(3.000000) 228: mad r2.w, r2.w, l(-2.000000), r5.z These lines calculate the S-curve values for the scales based on the fractional part of UV, as is the case with lightning. So:
float s_curve( float x ) { float x2 = x * x; float x3 = x2 * x; // -2x^3 + 3x^2 return -2.0*x3 + 3.0*x2; } ... // lines 217-222 float weightX = 1.0 - frac( starsUV.x ); weightX = s_curve( weightX ); // lines 223-228 float weightY = 1.0 - frac( starsUV.y ); weightY = s_curve( weightY ); As you might expect, these coefficients are used to smoothly interpolate the noise and generate the final offset for the sampling coordinates:
229: mad r4.w, r4.w, l(0.000000001), -r5.x 230: mad r4.w, r0.w, r4.w, r5.x float noise0 = lerp( fStarsNoise1, fStarsNoise2, weightX ); 231: mad r5.x, r5.y, l(0.000000001), -r1.w 232: mad r0.w, r0.w, r5.x, r1.w float noise1 = lerp( fStarsNoise3, fStarsNoise4, weightX ); 233: add r0.w, -r4.w, r0.w 234: mad r0.w, r2.w, r0.w, r4.w float offset = lerp( noise0, noise1, weightY ); 235: mad r2.xyz, r0.wwww, l(0.000500, 0.000500, 0.000500, 0.000000), r2.xyzx 236: sample_indexable(texturecube)(float,float,float,float) r2.xyz, r2.xyzx, t0.xyzw, s0 float3 starsPerturbedDir = dirXYZ + offset * 0.0005; float3 starsColorDisturbed = texNightStars.Sample( samplerAnisoWrap, starsPerturbedDir ).rgb; Here is a small visualization of the calculated offset :
After calculating starsColorDisturbed, the hardest part is complete. Hooray!
The next stage is performing gamma correction for both starsColor and starsColorDisturbed , after which they are multiplied:
starsColor = pow( starsColor, 2.2 ); starsColorDisturbed = pow( starsColorDisturbed, 2.2 ); float3 starsFinal = starsColor * starsColorDisturbed; Stars - the final touches
We have starsFinal in r1.xyz. At the end of the processing of stars, the following occurs:
256: log r1.xyz, r1.xyzx 257: mul r1.xyz, r1.xyzx, l(2.500000, 2.500000, 2.500000, 0.000000) 258: exp r1.xyz, r1.xyzx 259: min r1.xyz, r1.xyzx, l(1.000000, 1.000000, 1.000000, 0.000000) 260: add r0.w, -cb0[9].w, l(1.000000) 261: mul r1.xyz, r0.wwww, r1.xyzx 262: mul r1.xyz, r1.xyzx, l(10.000000, 10.000000, 10.000000, 0.000000) It is much easier compared to the twinkling and moving stars.
So, we start with the construction of starsFinal to the power of 2.5 - this allows us to control the density of stars. Pretty clever. Then we make the maximum color of the stars be float3 (1, 1, 1).
cb0 [9] .w is used to control the overall visibility of stars. Therefore, it can be expected that in the daytime this value is equal to 1.0 (which gives multiplication by zero), and at night - 0.0.
In the end, we increase the visibility of the stars by 10. And that's it!
Part 3. Witcher's scent (objects and brightness map)
Almost all of the previously described effects and techniques were not really related to Witcher 3. Things like tonal correction, vignetting, or calculating average brightness are present in almost every modern game. Even the effect of intoxication is quite common.
That is why I decided to take a closer look at the mechanics of rendering "witch's flair". Geralt is a witcher, and therefore his feelings are much sharper than those of an ordinary person. Consequently, he can see and hear more than other people, which greatly helps him in investigations. Witcher's mechanics allow the player to visualize such traces.
Here is a demonstration of the effect:
And one more, with better lighting:
As you can see, there are two types of objects: those with which Geralt can interact (yellow counter) and traces associated with the investigation (red outline). After Geralt examines the red trail, he can turn into yellow (first video). Note that the entire screen becomes grayer and the “fish eye” effect is added (second video).
This effect is quite complex, so I decided to divide his study into three parts.
In the first one I will talk about the selection of objects, in the second - about the contour generation, and in the third - about the final merging of all this into one whole.
Object selection
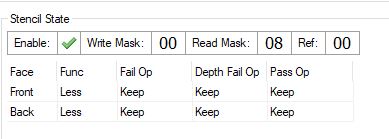
As I said, there are two types of objects, and we need to distinguish them. In Witcher 3 this is implemented using stencil buffer. When generating GBuffer meshes, which should be marked as “traces” (red), they are rendered with stencil = 8. The meshes marked with yellow as “interesting” objects are rendered with stencil = 4.
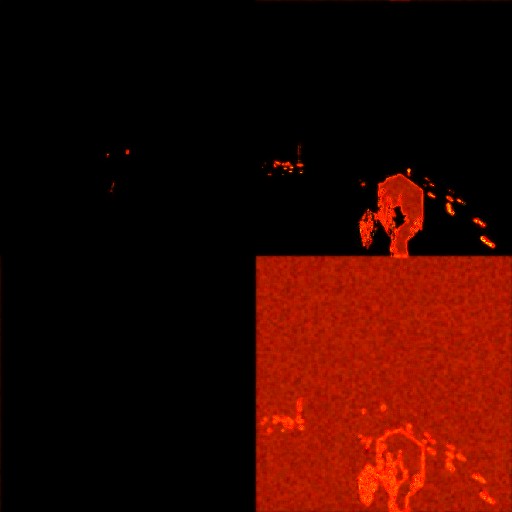
For example, the following two textures show an example frame with visible witch sneak and the corresponding stencil buffer:


Briefly about the stencil buffer
Stencil buffer is often used in games for tagging meshes. Certain mesh categories are assigned the same ID.
The idea is to use the Always function with the Replace operator if the stencil test was successful, and with the Keep operator in all other cases.
Here is how it is implemented using the D3D11:
D3D11_DEPTH_STENCIL_DESC depthstencilState; // Set depth parameters.... // Enable stencil depthstencilState.StencilEnable = TRUE; // Read & write all bits depthstencilState.StencilReadMask = 0xFF; depthstencilState.StencilWriteMask = 0xFF; // Stencil operator for front face depthstencilState.FrontFace.StencilFunc = D3D11_COMPARISON_ALWAYS; depthstencilState.FrontFace.StencilDepthFailOp = D3D11_STENCIL_OP_KEEP; depthstencilState.FrontFace.StencilFailOp = D3D11_STENCIL_OP_KEEP; depthstencilState.FrontFace.StencilPassOp = D3D11_STENCIL_OP_REPLACE; // Stencil operator for back face. depthstencilState.BackFace.StencilFunc = D3D11_COMPARISON_ALWAYS; depthstencilState.BackFace.StencilDepthFailOp = D3D11_STENCIL_OP_KEEP; depthstencilState.BackFace.StencilFailOp = D3D11_STENCIL_OP_KEEP; depthstencilState.BackFace.StencilPassOp = D3D11_STENCIL_OP_REPLACE; pDevice->CreateDepthStencilState( &depthstencilState, &m_pDS_AssignValue ); The stencil value to be written into the buffer is passed as StencilRef in the API call:
// from now on set stencil buffer values to 8 pDevCon->OMSetDepthStencilState( m_pDS_AssignValue, 8 ); ... pDevCon->DrawIndexed( ... ); Rendering brightness
In this passage, from the point of view of implementation, there is one full-screen texture in the R11G11B10_FLOAT format, in which interesting objects and tracks are stored in the R and G channels.
Why do we need this in terms of brightness? It turns out that Geralt's scent has a limited radius, so objects get contours only when the player is close enough to them.
See this aspect in action:

We start by cleaning the brightness texture by filling it with black.
Then two full-screen draw calls are executed: the first for the “track”, the second for interesting objects:
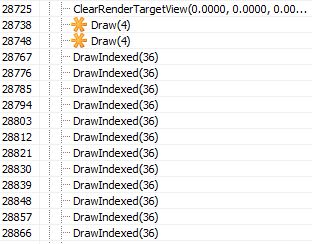
The first draw call is made for traces - the green channel:

The second call is made for interesting objects - the red channel:

Ok, but how do we determine which pixels to consider? We'll have to use the stencil buffer!
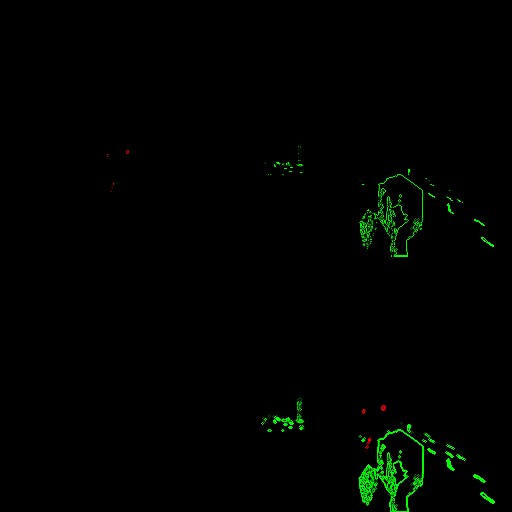
For each of these calls, the stencil test is performed, and only those pixels that were previously labeled as “8” (the first draw call) or “4” are received.
Visualization of the stencil test for traces:

... and for interesting objects:

How is the test performed in this case? The basics of stencil testing can be found in a good post . In general, the formula stencil test has the following form:
if (StencilRef & StencilReadMask OP StencilValue & StencilReadMask) accept pixel else discard pixel Where:
StencilRef is the value passed by the API call,
StencilReadMask is the mask used to read the stencil value (note that it is present on the left and on the right side),
OP is the comparison operator specified via the API,
StencilValue is the stencil buffer value in the current processed pixel.
It is important to understand that we use binary AND to compute the operands.
After getting familiar with the basics, let's see how these parameters are used in these draw calls:
Condition stencil for traces

Condition stencil for interesting objects
Ha!As we can see, the only difference is in ReadMask. Let's check it out! Substitute these values into the stencil test equation:
Let StencilReadMask = 0x08 and StencilRef = 0: For a pixel with stencil = 8: 0 & 0x08 < 8 & 0x08 0 < 8 TRUE For a pixel with stencil = 4: 0 & 0x08 < 4 & 0x08 0 < 0 FALSE Clever. As you can see, in this case we compare not the stencil value, but check whether a certain stencil buffer bit is set. Each pixel of stencil buffer has the format uint8, therefore the interval of values is [0-255].
Note: All DrawIndexed (36) calls are associated with rendering footprints as footprints, so in this particular frame, the brightness map has the following final appearance:

But before the stencil test there is a pixel shader. Both 28738 and 28748 use the same pixel shader:
ps_5_0 dcl_globalFlags refactoringAllowed dcl_constantbuffer cb0[2], immediateIndexed dcl_constantbuffer cb3[8], immediateIndexed dcl_constantbuffer cb12[214], immediateIndexed dcl_sampler s15, mode_default dcl_resource_texture2d (float,float,float,float) t15 dcl_input_ps_siv v0.xy, position dcl_output o0.xyzw dcl_output o1.xyzw dcl_output o2.xyzw dcl_output o3.xyzw dcl_temps 2 0: mul r0.xy, v0.xyxx, cb0[1].zwzz 1: sample_indexable(texture2d)(float,float,float,float) r0.x, r0.xyxx, t15.xyzw, s15 2: mul r1.xyzw, v0.yyyy, cb12[211].xyzw 3: mad r1.xyzw, cb12[210].xyzw, v0.xxxx, r1.xyzw 4: mad r0.xyzw, cb12[212].xyzw, r0.xxxx, r1.xyzw 5: add r0.xyzw, r0.xyzw, cb12[213].xyzw 6: div r0.xyz, r0.xyzx, r0.wwww 7: add r0.xyz, r0.xyzx, -cb3[7].xyzx 8: dp3 r0.x, r0.xyzx, r0.xyzx 9: sqrt r0.x, r0.x 10: mul r0.y, r0.x, l(0.120000) 11: log r1.x, abs(cb3[6].y) 12: mul r1.xy, r1.xxxx, l(2.800000, 0.800000, 0.000000, 0.000000) 13: exp r1.xy, r1.xyxx 14: mad r0.zw, r1.xxxy, l(0.000000, 0.000000, 120.000000, 120.000000), l(0.000000, 0.000000, 1.000000, 1.000000) 15: lt r1.x, l(0.030000), cb3[6].y 16: movc r0.xy, r1.xxxx, r0.yzyy, r0.xwxx 17: div r0.x, r0.x, r0.y 18: log r0.x, r0.x 19: mul r0.x, r0.x, l(1.600000) 20: exp r0.x, r0.x 21: add r0.x, -r0.x, l(1.000000) 22: max r0.x, r0.x, l(0) 23: mul o0.xyz, r0.xxxx, cb3[0].xyzx 24: mov o0.w, cb3[0].w 25: mov o1.xyzw, cb3[1].xyzw 26: mov o2.xyzw, cb3[2].xyzw 27: mov o3.xyzw, cb3[3].xyzw 28: ret This pixel shader writes only in one render target, so lines 24-27 are redundant.
The first thing that happens here is depth sampling (a point sampler with limiting values), line 1. This value is used to recreate a position in the world by multiplying with a special matrix followed by dividing it (lines 2-6).
Taking the position of Geralt (cb3 [7] .xyz - note that this is not the camera position!), We calculate the distance from Geralt to this particular point (lines 7-9).
The following input data
is important in this shader: - cb3 [0]. Rgb - output color. It can be float3 (0, 1, 0) (traces) or float3 (1, 0, 0) (interesting objects),
- cb3 [6] .y - distance scaling factor. It directly affects the radius and brightness of the final output.
Later we have rather cunning formulas for calculating brightness depending on the distance between Geralt and the object. I can assume that all coefficients are chosen experimentally.
The final output is color * intensity .
The HLSL code will look something like this:
struct FSInput { float4 param0 : SV_Position; }; struct FSOutput { float4 param0 : SV_Target0; float4 param1 : SV_Target1; float4 param2 : SV_Target2; float4 param3 : SV_Target3; }; float3 getWorldPos( float2 screenPos, float depth ) { float4 worldPos = float4(screenPos, depth, 1.0); worldPos = mul( worldPos, screenToWorld ); return worldPos.xyz / worldPos.w; } FSOutput EditedShaderPS(in FSInput IN) { // * Inputs // Directly affects radius of the effect float distanceScaling = cb3_v6.y; // Color of output at the end float3 color = cb3_v0.rgb; // Sample depth float2 uv = IN.param0.xy * cb0_v1.zw; float depth = texture15.Sample( sampler15, uv ).x; // Reconstruct world position float3 worldPos = getWorldPos( IN.param0.xy, depth ); // Calculate distance from Geralt to world position of particular object float dist_geraltToWorld = length( worldPos - cb3_v7.xyz ); // Calculate two squeezing params float t0 = 1.0 + 120*pow( abs(distanceScaling), 2.8 ); float t1 = 1.0 + 120*pow( abs(distanceScaling), 0.8 ); // Determine nominator and denominator float2 params; params = (distanceScaling > 0.03) ? float2(dist_geraltToWorld * 0.12, t0) : float2(dist_geraltToWorld, t1); // Distance Geralt <-> Object float nominator = params.x; // Hiding factor float denominator = params.y; // Raise to power of 1.6 float param = pow( params.x / params.y, 1.6 ); // Calculate final intensity float intensity = max(0.0, 1.0 - param ); // * Final outputs. // * // * This PS outputs only one color, the rest // * is redundant. I just added this to keep 1-1 ratio with // * original assembly. FSOutput OUT = (FSOutput)0; OUT.param0.xyz = color * intensity; // == redundant == OUT.param0.w = cb3_v0.w; OUT.param1 = cb3_v1; OUT.param2 = cb3_v2; OUT.param3 = cb3_v3; // =============== return OUT; } A small comparison of the original (left) and my (right) assembler shader code.

This was the first stage of the witch's flair effect . In fact, it is the easiest.
Part 4. Witcher scent (contour map)
Take another look at the scene we are investigating:

In the first part of the analysis of the effect of witch's flair, I showed how the “brightness map” is generated.
We have one full-screen texture format R11G11B10_FLOAT, which may look like this:

The green channel means “traces”, the red one - interesting objects with which Geralt can interact.
Having received this texture, we can proceed to the next stage - I called it “contour map”.
This is a slightly weird texture format 512x512 R16G16_FLOAT. It is important that it is implemented in the style of "ping-pong". The contour map from the previous frame is input (along with the brightness map) for generating a new contour map in the current frame.
Ping-pong buffers can be implemented in a variety of ways, but I personally like the following (pseudo-code) the most:
// Declarations Texture2D m_texOutlineMap[2]; uint m_outlineIndex = 0; // Rendering void Render() { pDevCon->SetInputTexture( m_texOutlineMap[m_outlineIndex] ); pDevCon->SetOutputTexture( m_texOutlineMap[!m_outlineIndex] ); ... pDevCon->Draw(...); // after draw m_outlineIndex = !m_outlineIndex; } This approach, in which the input is always [m_outlineIndex] and the output is always [! M_outlineIndex] , provides flexibility with respect to the use of further post-effects.
Let's take a look at the pixel shader:
ps_5_0 dcl_globalFlags refactoringAllowed dcl_constantbuffer cb3[1], immediateIndexed dcl_sampler s0, mode_default dcl_sampler s1, mode_default dcl_resource_texture2d (float,float,float,float) t0 dcl_resource_texture2d (float,float,float,float) t1 dcl_input_ps linear v2.xy dcl_output o0.xyzw dcl_temps 4 0: add r0.xyzw, v2.xyxy, v2.xyxy 1: round_ni r1.xy, r0.zwzz 2: frc r0.xyzw, r0.xyzw 3: add r1.zw, r1.xxxy, l(0.000000, 0.000000, -1.000000, -1.000000) 4: dp2 r1.z, r1.zwzz, r1.zwzz 5: add r1.z, -r1.z, l(1.000000) 6: max r2.w, r1.z, l(0) 7: dp2 r1.z, r1.xyxx, r1.xyxx 8: add r3.xyzw, r1.xyxy, l(-1.000000, -0.000000, -0.000000, -1.000000) 9: add r1.x, -r1.z, l(1.000000) 10: max r2.x, r1.x, l(0) 11: dp2 r1.x, r3.xyxx, r3.xyxx 12: dp2 r1.y, r3.zwzz, r3.zwzz 13: add r1.xy, -r1.xyxx, l(1.000000, 1.000000, 0.000000, 0.000000) 14: max r2.yz, r1.xxyx, l(0, 0, 0, 0) 15: sample_indexable(texture2d)(float,float,float,float) r1.xyzw, r0.zwzz, t1.xyzw, s1 16: dp4 r1.x, r1.xyzw, r2.xyzw 17: add r2.xyzw, r0.zwzw, l(0.003906, 0.000000, -0.003906, 0.000000) 18: add r0.xyzw, r0.xyzw, l(0.000000, 0.003906, 0.000000, -0.003906) 19: sample_indexable(texture2d)(float,float,float,float) r1.yz, r2.xyxx, t1.zxyw, s1 20: sample_indexable(texture2d)(float,float,float,float) r2.xy, r2.zwzz, t1.xyzw, s1 21: add r1.yz, r1.yyzy, -r2.xxyx 22: sample_indexable(texture2d)(float,float,float,float) r0.xy, r0.xyxx, t1.xyzw, s1 23: sample_indexable(texture2d)(float,float,float,float) r0.zw, r0.zwzz, t1.zwxy, s1 24: add r0.xy, -r0.zwzz, r0.xyxx 25: max r0.xy, abs(r0.xyxx), abs(r1.yzyy) 26: min r0.xy, r0.xyxx, l(1.000000, 1.000000, 0.000000, 0.000000) 27: mul r0.xy, r0.xyxx, r1.xxxx 28: sample_indexable(texture2d)(float,float,float,float) r0.zw, v2.xyxx, t0.zwxy, s0 29: mad r0.w, r1.x, l(0.150000), r0.w 30: mad r0.x, r0.x, l(0.350000), r0.w 31: mad r0.x, r0.y, l(0.350000), r0.x 32: mul r0.yw, cb3[0].zzzw, l(0.000000, 300.000000, 0.000000, 300.000000) 33: mad r0.yw, v2.xxxy, l(0.000000, 150.000000, 0.000000, 150.000000), r0.yyyw 34: ftoi r0.yw, r0.yyyw 35: bfrev r0.w, r0.w 36: iadd r0.y, r0.w, r0.y 37: ishr r0.w, r0.y, l(13) 38: xor r0.y, r0.y, r0.w 39: imul null, r0.w, r0.y, r0.y 40: imad r0.w, r0.w, l(0x0000ec4d), l(0.0000000000000000000000000000000000001) 41: imad r0.y, r0.y, r0.w, l(146956042240.000000) 42: and r0.y, r0.y, l(0x7fffffff) 43: itof r0.y, r0.y 44: mad r0.y, r0.y, l(0.000000001), l(0.650000) 45: add_sat r1.xyzw, v2.xyxy, l(0.001953, 0.000000, -0.001953, 0.000000) 46: sample_indexable(texture2d)(float,float,float,float) r0.w, r1.xyxx, t0.yzwx, s0 47: sample_indexable(texture2d)(float,float,float,float) r1.x, r1.zwzz, t0.xyzw, s0 48: add r0.w, r0.w, r1.x 49: add_sat r1.xyzw, v2.xyxy, l(0.000000, 0.001953, 0.000000, -0.001953) 50: sample_indexable(texture2d)(float,float,float,float) r1.x, r1.xyxx, t0.xyzw, s0 51: sample_indexable(texture2d)(float,float,float,float) r1.y, r1.zwzz, t0.yxzw, s0 52: add r0.w, r0.w, r1.x 53: add r0.w, r1.y, r0.w 54: mad r0.w, r0.w, l(0.250000), -r0.z 55: mul r0.w, r0.y, r0.w 56: mul r0.y, r0.y, r0.z 57: mad r0.x, r0.w, l(0.900000), r0.x 58: mad r0.y, r0.y, l(-0.240000), r0.x 59: add r0.x, r0.y, r0.z 60: mov_sat r0.z, cb3[0].x 61: log r0.z, r0.z 62: mul r0.z, r0.z, l(100.000000) 63: exp r0.z, r0.z 64: mad r0.z, r0.z, l(0.160000), l(0.700000) 65: mul o0.xy, r0.zzzz, r0.xyxx 66: mov o0.zw, l(0, 0, 0, 0) 67: ret As you can see, the output contour map is divided into four equal squares, and this is the first thing we need to learn:
0: add r0.xyzw, v2.xyxy, v2.xyxy 1: round_ni r1.xy, r0.zwzz 2: frc r0.xyzw, r0.xyzw 3: add r1.zw, r1.xxxy, l(0.000000, 0.000000, -1.000000, -1.000000) 4: dp2 r1.z, r1.zwzz, r1.zwzz 5: add r1.z, -r1.z, l(1.000000) 6: max r2.w, r1.z, l(0) 7: dp2 r1.z, r1.xyxx, r1.xyxx 8: add r3.xyzw, r1.xyxy, l(-1.000000, -0.000000, -0.000000, -1.000000) 9: add r1.x, -r1.z, l(1.000000) 10: max r2.x, r1.x, l(0) 11: dp2 r1.x, r3.xyxx, r3.xyxx 12: dp2 r1.y, r3.zwzz, r3.zwzz 13: add r1.xy, -r1.xyxx, l(1.000000, 1.000000, 0.000000, 0.000000) 14: max r2.yz, r1.xxyx, l(0, 0, 0, 0) We start by calculating the floor (TextureUV * 2.0), which gives us the following:

A small function is used to define individual squares:
float getParams(float2 uv) { float d = dot(uv, uv); d = 1.0 - d; d = max( d, 0.0 ); return d; } Notice that the function returns 1.0 with the input float2 (0.0, 0.0).
This case occurs in the upper left corner. To get the same situation in the upper right corner, you need to subtract float2 (1, 0) from the rounded texcoords, subtract float2 (0, 1) for the green square, and float2 (1.0, 1.0) for the yellow square.
So:
float2 flooredTextureUV = floor( 2.0 * TextureUV ); ... float2 uv1 = flooredTextureUV; float2 uv2 = flooredTextureUV + float2(-1.0, -0.0); float2 uv3 = flooredTextureUV + float2( -0.0, -1.0); float2 uv4 = flooredTextureUV + float2(-1.0, -1.0); float4 mask; mask.x = getParams( uv1 ); mask.y = getParams( uv2 ); mask.z = getParams( uv3 ); mask.w = getParams( uv4 ); Each of the mask components is either zero or one, and is responsible for one square of the texture. For example, mask.r and mask.w :

mask.r

mask.w
We got a mask , let's move on. Line 15 samples the brightness map. Note that the brightness texture has the format R11G11B10_FLOAT, although we sample all the components of rgba. In this situation, it is assumed that .a is 1.0f.
Texcoords used for this operation can be calculated as frac (TextureUV * 2.0) . Therefore, the result of this operation may, for example, look like this:

See the similarities?
The next stage is very clever - a four-component scalar product (dp4) is performed:
16: dp4 r1.x, r1.xyzw, r2.xyzw Thus, only the red channel remains in the upper left corner (that is, only interesting objects), only the green channel in the upper right (only traces), and everything in the lower right (because the brightness component .w is indirectly set to 1.0). Great idea. The result of the dot product looks like this:

Having received this masterFilter , we are ready to determine the contours of objects. It is not as difficult as it may seem.The algorithm is very similar to that used when getting sharpness - we need to get the maximum absolute difference of values.
Here's what happens: we sample four texels next to the current processed texel (important: in this case, the texel size is 1.0 / 256.0!) And we calculate the maximum absolute differences for the red and green channels:
float fTexel = 1.0 / 256; float2 sampling1 = TextureUV + float2( fTexel, 0 ); float2 sampling2 = TextureUV + float2( -fTexel, 0 ); float2 sampling3 = TextureUV + float2( 0, fTexel ); float2 sampling4 = TextureUV + float2( 0, -fTexel ); float2 intensity_x0 = texIntensityMap.Sample( sampler1, sampling1 ).xy; float2 intensity_x1 = texIntensityMap.Sample( sampler1, sampling2 ).xy; float2 intensity_diff_x = intensity_x0 - intensity_x1; float2 intensity_y0 = texIntensityMap.Sample( sampler1, sampling3 ).xy; float2 intensity_y1 = texIntensityMap.Sample( sampler1, sampling4 ).xy; float2 intensity_diff_y = intensity_y0 - intensity_y1; float2 maxAbsDifference = max( abs(intensity_diff_x), abs(intensity_diff_y) ); maxAbsDifference = saturate(maxAbsDifference); Now if we multiply the filter by maxAbsDifference ...
Very simple and effective.
After receiving the contours, we sample the contour map from the previous frame.
Then, in order to get the “ghost” effect, we take a part of the parameters calculated on the current pass and the values from the contour map.
Say hello to our old friend - an integer noise. He is present here. Animation parameters (cb3 [0] .zw) are taken from the buffer of constants and change over time.
float2 outlines = masterFilter * maxAbsDifference; // Sample outline map float2 outlineMap = texOutlineMap.Sample( samplerLinearWrap, uv ).xy; // I guess it's related with ghosting float paramOutline = masterFilter*0.15 + outlineMap.y; paramOutline += 0.35 * outlines.r; paramOutline += 0.35 * outlines.g; // input for integer noise float2 noiseWeights = cb3_v0.zw; float2 noiseInputs = 150.0*uv + 300.0*noiseWeights; int2 iNoiseInputs = (int2) noiseInputs; float noise0 = clamp( integerNoise( iNoiseInputs.x + reversebits(iNoiseInputs.y) ), -1, 1 ) + 0.65; // r0.y Note: if you want to realize your wit’s own flair, I recommend limiting the integer noise to the interval [-1; 1] (as stated on its website). In the original TW3 shader, there was no limit, but without it I would get terrible artifacts and the whole map of the contours was unstable.
Then we sample the contour map in the same way as the brightness map earlier (this time the texel has a size of 1.0 / 512.0), and calculate the average value of the .x component:
// sampling of outline map fTexel = 1.0 / 512.0; sampling1 = saturate( uv + float2( fTexel, 0 ) ); sampling2 = saturate( uv + float2( -fTexel, 0 ) ); sampling3 = saturate( uv + float2( 0, fTexel ) ); sampling4 = saturate( uv + float2( 0, -fTexel ) ); float outline_x0 = texOutlineMap.Sample( sampler0, sampling1 ).x; float outline_x1 = texOutlineMap.Sample( sampler0, sampling2 ).x; float outline_y0 = texOutlineMap.Sample( sampler0, sampling3 ).x; float outline_y1 = texOutlineMap.Sample( sampler0, sampling4 ).x; float averageOutline = (outline_x0+outline_x1+outline_y0+outline_y1) / 4.0; Then, judging by the assembler code, the difference between the average and the value of this particular pixel is calculated, after which the integer noise is distorted:
// perturb with noise float frameOutlineDifference = averageOutline - outlineMap.x; frameOutlineDifference *= noise0; The next step is to distort the value from the “old” contour map using noise - this is the main line, giving the output texture a blocky feeling.
Then there are other calculations, after which, at the very end, the attenuation is calculated.
// the main place with gives blocky look of texture float newNoise = outlineMap.x * noise0; float newOutline = frameOutlineDifference * 0.9 + paramOutline; newOutline -= 0.24*newNoise; // 59: add r0.x, r0.y, r0.z float2 finalOutline = float2( outlineMap.x + newOutline, newOutline); // * calculate damping float dampingParam = saturate( cb3_v0.x ); dampingParam = pow( dampingParam, 100 ); float damping = 0.7 + 0.16*dampingParam; // * final multiplication float2 finalColor = finalOutline * damping; return float4(finalColor, 0, 0); Here is a short video showing a contour map in action:
If you are interested in a full pixel shader, then it is laid out here . Shader compatible with RenderDoc.
It is interesting (and, frankly, slightly annoying) that despite the fact that the assembler code is identical with the original shader from Witcher 3, the final appearance of the map of the contours in RenderDoc changes!
Note: in the last pass (see the next section) you will see that only the .r map of the contour channel is used. Why then do we need the .g channel? I think this is some kind of ping-pong buffer in one texture - notice that .r contains the .g channel + some new value.
Part 5: Witcher's Scent ("fisheye" and the final result)
Let us briefly list what we already have: in the first part, devoted to the witty scent, a full-screen brightness map was generated, indicating how noticeable the effect should be depending on the distance. In the second part, I explored the contour map in more detail, which is responsible for the contours and animation of the finished effect.
We have reached the final stage. All this needs to be combined! The last pass is a full-screen quad. Input data: color buffer, edge map and brightness map.
Before:

After:

Once again I will show the video with the effect applied:
As you can see, besides overlaying contours on objects that Geralt can see or hear, the fish-eye effect is applied to the entire screen, and the entire screen (especially the corners) becomes grayish to convey the sensation of a real monster hunter.
Full assembler pixel shader code:
ps_5_0 dcl_globalFlags refactoringAllowed dcl_constantbuffer cb0[3], immediateIndexed dcl_constantbuffer cb3[7], immediateIndexed dcl_sampler s0, mode_default dcl_sampler s2, mode_default dcl_resource_texture2d (float,float,float,float) t0 dcl_resource_texture2d (float,float,float,float) t2 dcl_resource_texture2d (float,float,float,float) t3 dcl_input_ps_siv v0.xy, position dcl_output o0.xyzw dcl_temps 7 0: div r0.xy, v0.xyxx, cb0[2].xyxx 1: mad r0.zw, r0.xxxy, l(0.000000, 0.000000, 2.000000, 2.000000), l(0.000000, 0.000000, -1.000000, -1.000000) 2: mov r1.yz, abs(r0.zzwz) 3: div r0.z, cb0[2].x, cb0[2].y 4: mul r1.x, r0.z, r1.y 5: add r0.zw, r1.xxxz, -cb3[2].xxxy 6: mul_sat r0.zw, r0.zzzw, l(0.000000, 0.000000, 0.555556, 0.555556) 7: log r0.zw, r0.zzzw 8: mul r0.zw, r0.zzzw, l(0.000000, 0.000000, 2.500000, 2.500000) 9: exp r0.zw, r0.zzzw 10: dp2 r0.z, r0.zwzz, r0.zwzz 11: sqrt r0.z, r0.z 12: min r0.z, r0.z, l(1.000000) 13: add r0.z, -r0.z, l(1.000000) 14: mov_sat r0.w, cb3[6].x 15: add_sat r1.xy, -r0.xyxx, l(0.030000, 0.030000, 0.000000, 0.000000) 16: add r1.x, r1.y, r1.x 17: add_sat r0.xy, r0.xyxx, l(-0.970000, -0.970000, 0.000000, 0.000000) 18: add r0.x, r0.x, r1.x 19: add r0.x, r0.y, r0.x 20: mul r0.x, r0.x, l(20.000000) 21: min r0.x, r0.x, l(1.000000) 22: add r1.xy, v0.xyxx, v0.xyxx 23: div r1.xy, r1.xyxx, cb0[2].xyxx 24: add r1.xy, r1.xyxx, l(-1.000000, -1.000000, 0.000000, 0.000000) 25: dp2 r0.y, r1.xyxx, r1.xyxx 26: mul r1.xy, r0.yyyy, r1.xyxx 27: mul r0.y, r0.w, l(0.100000) 28: mul r1.xy, r0.yyyy, r1.xyxx 29: max r1.xy, r1.xyxx, l(-0.400000, -0.400000, 0.000000, 0.000000) 30: min r1.xy, r1.xyxx, l(0.400000, 0.400000, 0.000000, 0.000000) 31: mul r1.xy, r1.xyxx, cb3[1].xxxx 32: mul r1.zw, r1.xxxy, cb0[2].zzzw 33: mad r1.zw, v0.xxxy, cb0[1].zzzw, -r1.zzzw 34: sample_indexable(texture2d)(float,float,float,float) r2.xyz, r1.zwzz, t0.xyzw, s0 35: mul r3.xy, r1.zwzz, l(0.500000, 0.500000, 0.000000, 0.000000) 36: sample_indexable(texture2d)(float,float,float,float) r0.y, r3.xyxx, t2.yxzw, s2 37: mad r3.xy, r1.zwzz, l(0.500000, 0.500000, 0.000000, 0.000000), l(0.500000, 0.000000, 0.000000, 0.000000) 38: sample_indexable(texture2d)(float,float,float,float) r2.w, r3.xyxx, t2.yzwx, s2 39: mul r2.w, r2.w, l(0.125000) 40: mul r3.x, cb0[0].x, l(0.100000) 41: add r0.x, -r0.x, l(1.000000) 42: mul r0.xy, r0.xyxx, l(0.030000, 0.125000, 0.000000, 0.000000) 43: mov r3.yzw, l(0, 0, 0, 0) 44: mov r4.x, r0.y 45: mov r4.y, r2.w 46: mov r4.z, l(0) 47: loop 48: ige r4.w, r4.z, l(8) 49: breakc_nz r4.w 50: itof r4.w, r4.z 51: mad r4.w, r4.w, l(0.785375), -r3.x 52: sincos r5.x, r6.x, r4.w 53: mov r6.y, r5.x 54: mul r5.xy, r0.xxxx, r6.xyxx 55: mad r5.zw, r5.xxxy, l(0.000000, 0.000000, 0.125000, 0.125000), r1.zzzw 56: mul r6.xy, r5.zwzz, l(0.500000, 0.500000, 0.000000, 0.000000) 57: sample_indexable(texture2d)(float,float,float,float) r4.w, r6.xyxx, t2.yzwx, s2 58: mad r4.x, r4.w, l(0.125000), r4.x 59: mad r5.zw, r5.zzzw, l(0.000000, 0.000000, 0.500000, 0.500000), l(0.000000, 0.000000, 0.500000, 0.000000) 60: sample_indexable(texture2d)(float,float,float,float) r4.w, r5.zwzz, t2.yzwx, s2 61: mad r4.y, r4.w, l(0.125000), r4.y 62: mad r5.xy, r5.xyxx, r1.xyxx, r1.zwzz 63: sample_indexable(texture2d)(float,float,float,float) r5.xyz, r5.xyxx, t0.xyzw, s0 64: mad r3.yzw, r5.xxyz, l(0.000000, 0.125000, 0.125000, 0.125000), r3.yyzw 65: iadd r4.z, r4.z, l(1) 66: endloop 67: sample_indexable(texture2d)(float,float,float,float) r0.xy, r1.zwzz, t3.xyzw, s0 68: mad_sat r0.xy, -r0.xyxx, l(0.800000, 0.750000, 0.000000, 0.000000), r4.xyxx 69: dp3 r1.x, r3.yzwy, l(0.300000, 0.300000, 0.300000, 0.000000) 70: add r1.yzw, -r1.xxxx, r3.yyzw 71: mad r1.xyz, r0.zzzz, r1.yzwy, r1.xxxx 72: mad r1.xyz, r1.xyzx, l(0.600000, 0.600000, 0.600000, 0.000000), -r2.xyzx 73: mad r1.xyz, r0.wwww, r1.xyzx, r2.xyzx 74: mul r0.yzw, r0.yyyy, cb3[4].xxyz 75: mul r2.xyz, r0.xxxx, cb3[5].xyzx 76: mad r0.xyz, r0.yzwy, l(1.200000, 1.200000, 1.200000, 0.000000), r2.xyzx 77: mov_sat r2.xyz, r0.xyzx 78: dp3_sat r0.x, r0.xyzx, l(1.000000, 1.000000, 1.000000, 0.000000) 79: add r0.yzw, -r1.xxyz, r2.xxyz 80: mad o0.xyz, r0.xxxx, r0.yzwy, r1.xyzx 81: mov o0.w, l(1.000000) 82: ret 82 lines - it means we have a lot of work!
First, take a look at the incoming data:
// *** Inputs // * Zoom amount, always 1 float zoomAmount = cb3_v1.x; // Another value which affect fisheye effect // but always set to float2(1.0, 1.0). float2 amount = cb0_v2.zw; // Elapsed time in seconds float time = cb0_v0.x; // Colors of witcher senses float3 colorInteresting = cb3_v5.rgb; float3 colorTraces = cb3_v4.rgb; // Was always set to float2(0.0, 0.0). // Setting this to higher values // makes "grey corners" effect weaker. float2 offset = cb3_v2.xy; // Dimensions of fullscreen float2 texSize = cb0_v2.xy; float2 invTexSize = cb0_v1.zw; // Main value which causes fisheye effect [0-1] const float fisheyeAmount = saturate( cb3_v6.x ); The primary value responsible for the magnitude of the effect is fisheyeAmount . I think it gradually rises from 0.0 to 1.0, when Geralt begins to use his instinct. The remaining values do not change much, but I suspect that some of them would be different if the user had turned off the fisheye effect in the options (I did not check it).
The first thing that happens here is that the shader computes the mask responsible for the gray corners:
0: div r0.xy, v0.xyxx, cb0[2].xyxx 1: mad r0.zw, r0.xxxy, l(0.000000, 0.000000, 2.000000, 2.000000), l(0.000000, 0.000000, -1.000000, -1.000000) 2: mov r1.yz, abs(r0.zzwz) 3: div r0.z, cb0[2].x, cb0[2].y 4: mul r1.x, r0.z, r1.y 5: add r0.zw, r1.xxxz, -cb3[2].xxxy 6: mul_sat r0.zw, r0.zzzw, l(0.000000, 0.000000, 0.555556, 0.555556) 7: log r0.zw, r0.zzzw 8: mul r0.zw, r0.zzzw, l(0.000000, 0.000000, 2.500000, 2.500000) 9: exp r0.zw, r0.zzzw 10: dp2 r0.z, r0.zwzz, r0.zwzz 11: sqrt r0.z, r0.z 12: min r0.z, r0.z, l(1.000000) 13: add r0.z, -r0.z, l(1.000000) On HLSL we can write it as follows:
// Main uv float2 uv = PosH.xy / texSize; // Scale at first from [0-1] to [-1;1], then calculate abs float2 uv3 = abs( uv * 2.0 - 1.0); // Aspect ratio float aspectRatio = texSize.x / texSize.y; // * Mask used to make corners grey float mask_gray_corners; { float2 newUv = float2( uv3.x * aspectRatio, uv3.y ) - offset; newUv = saturate( newUv / 1.8 ); newUv = pow(newUv, 2.5); mask_gray_corners = 1-min(1.0, length(newUv) ); } First, the interval is calculated [-1; 1] UV and their absolute values. Then there is a tricky "squeeze". The finished mask looks like this:

I will return to this mask later.
Now I will intentionally skip a few lines of code and study the code responsible for the zoom effect more carefully.
22: add r1.xy, v0.xyxx, v0.xyxx 23: div r1.xy, r1.xyxx, cb0[2].xyxx 24: add r1.xy, r1.xyxx, l(-1.000000, -1.000000, 0.000000, 0.000000) 25: dp2 r0.y, r1.xyxx, r1.xyxx 26: mul r1.xy, r0.yyyy, r1.xyxx 27: mul r0.y, r0.w, l(0.100000) 28: mul r1.xy, r0.yyyy, r1.xyxx 29: max r1.xy, r1.xyxx, l(-0.400000, -0.400000, 0.000000, 0.000000) 30: min r1.xy, r1.xyxx, l(0.400000, 0.400000, 0.000000, 0.000000) 31: mul r1.xy, r1.xyxx, cb3[1].xxxx 32: mul r1.zw, r1.xxxy, cb0[2].zzzw 33: mad r1.zw, v0.xxxy, cb0[1].zzzw, -r1.zzzw First, the “doubled” texture coordinates are calculated and the float2 (1, 1) is subtracted:
float2 uv4 = 2 * PosH.xy; uv4 /= cb0_v2.xy; uv4 -= float2(1.0, 1.0); Such texcoord can be visualized like this:

Then the dot product (uv4, uv4) is calculated , which gives us a mask:

which is used to multiply the above texcoords:

Important: in the upper left corner (black pixels) the values are negative. They are displayed in black (0.0) due to the limited accuracy of the format R11G11B10_FLOAT. It does not have a sign bit, so negative values cannot be stored in it.
Then the attenuation coefficient is calculated (as I said above, fisheyeAmount changes from 0.0 to 1.0).
float attenuation = fisheyeAmount * 0.1; uv4 *= attenuation; Then the constraint (max / min) and one multiplication are performed.
This calculates the offset. To calculate the final uv to be used for sampling the color texture, we simply do the subtraction:
float2 colorUV = mainUv - offset;
When sampling the colorUV input texture , we get a distorted image next to the corners:

Contours
The next step is to sample the contour map to find the contours. It's pretty simple, first we find texcoords to sample the contours of interesting objects, and then do the same for the tracks:
// * Sample outline map // interesting objects (upper left square) float2 outlineUV = colorUV * 0.5; float outlineInteresting = texture2.Sample( sampler2, outlineUV ).x; // r0.y // traces (upper right square) outlineUV = colorUV * 0.5 + float2(0.5, 0.0); float outlineTraces = texture2.Sample( sampler2, outlineUV ).x; // r2.w outlineInteresting /= 8.0; // r4.x outlineTraces /= 8.0; // r4.y 
Interesting objects from the contour map

Traces from the contour map
It is worth noting that we sample only the .x channel from the contour map and only consider the upper squares.
Motion
To implement the movement of the tracks, almost the same trick is used as in the effect of intoxication. A single-size circle is added, and we sample the contour map 8 times for interesting objects and tracks, as well as the color texture.
Notice that we only divided the contours found by 8.0.
Since we are in the space of texture coordinates [0-1] 2 , the presence of a circle with a radius of 1 for enclosing a single pixel will create unacceptable artifacts:

Therefore, before moving on, let's find out how this radius is calculated. To do this, we need to go back to the missing lines 15-21. A minor problem with calculating this radius is that its calculation is scattered around the shader (possibly due to shader optimizations by the compiler). Therefore, here is the first part (15-21) and the second (41-42):
15: add_sat r1.xy, -r0.xyxx, l(0.030000, 0.030000, 0.000000, 0.000000) 16: add r1.x, r1.y, r1.x 17: add_sat r0.xy, r0.xyxx, l(-0.970000, -0.970000, 0.000000, 0.000000) 18: add r0.x, r0.x, r1.x 19: add r0.x, r0.y, r0.x 20: mul r0.x, r0.x, l(20.000000) 21: min r0.x, r0.x, l(1.000000) ... 41: add r0.x, -r0.x, l(1.000000) 42: mul r0.xy, r0.xyxx, l(0.030000, 0.125000, 0.000000, 0.000000) As you can see, we consider only texels from [0.00 - 0.03] next to each surface, sum up their values, multiply 20 and saturate. Here is what they look like after lines 15-21:

And here is how after line 41:

In line 42, we multiply this by 0.03, this value is the radius of the circle for the entire screen. As you can see, closer to the edges of the screen the radius becomes smaller.
Now we can look at the assembly code responsible for the movement:
40: mul r3.x, cb0[0].x, l(0.100000) 41: add r0.x, -r0.x, l(1.000000) 42: mul r0.xy, r0.xyxx, l(0.030000, 0.125000, 0.000000, 0.000000) 43: mov r3.yzw, l(0, 0, 0, 0) 44: mov r4.x, r0.y 45: mov r4.y, r2.w 46: mov r4.z, l(0) 47: loop 48: ige r4.w, r4.z, l(8) 49: breakc_nz r4.w 50: itof r4.w, r4.z 51: mad r4.w, r4.w, l(0.785375), -r3.x 52: sincos r5.x, r6.x, r4.w 53: mov r6.y, r5.x 54: mul r5.xy, r0.xxxx, r6.xyxx 55: mad r5.zw, r5.xxxy, l(0.000000, 0.000000, 0.125000, 0.125000), r1.zzzw 56: mul r6.xy, r5.zwzz, l(0.500000, 0.500000, 0.000000, 0.000000) 57: sample_indexable(texture2d)(float,float,float,float) r4.w, r6.xyxx, t2.yzwx, s2 58: mad r4.x, r4.w, l(0.125000), r4.x 59: mad r5.zw, r5.zzzw, l(0.000000, 0.000000, 0.500000, 0.500000), l(0.000000, 0.000000, 0.500000, 0.000000) 60: sample_indexable(texture2d)(float,float,float,float) r4.w, r5.zwzz, t2.yzwx, s2 61: mad r4.y, r4.w, l(0.125000), r4.y 62: mad r5.xy, r5.xyxx, r1.xyxx, r1.zwzz 63: sample_indexable(texture2d)(float,float,float,float) r5.xyz, r5.xyxx, t0.xyzw, s0 64: mad r3.yzw, r5.xxyz, l(0.000000, 0.125000, 0.125000, 0.125000), r3.yyzw 65: iadd r4.z, r4.z, l(1) 66: endloop Let's stop here for a minute. In line 40 we get the time coefficient - just elapsedTime * 0.1 . In line 43 we have a buffer for the texture of the color obtained inside the loop.
r0.x (lines 41-42) is, as we now know, the radius of the circle. r4.x (line 44) is the contour of interesting objects, r4.y (line 45) is the contour of the tracks (previously divided by 8!), and r4.z (line 46) is the loop counter.
As you might expect, the loop has 8 iterations. We start by calculating the angle in radians i * PI_4 , which gives us 2 * PI - a full circle. The angle is distorted over time.
Using sincos, we determine the sampling point (unit circle) and change the radius using multiplication (line 54).
After that we go round the pixel in a circle and sample the contours and color. After the cycle, we get the average values (due to the division by 8) contours and colors.
float timeParam = time * 0.1; // adjust circle radius circle_radius = 1.0 - circle_radius; circle_radius *= 0.03; float3 color_circle_main = float3(0.0, 0.0, 0.0); [loop] for (int i=0; 8 > i; i++) { // full 2*PI = 360 angles cycle const float angleRadians = (float) i * PI_4 - timeParam; // unit circle float2 unitCircle; sincos(angleRadians, unitCircle.y, unitCircle.x); // unitCircle.x = cos, unitCircle.y = sin // adjust radius unitCircle *= circle_radius; // * base texcoords (circle) - note we also scale radius here by 8 // * probably because of dimensions of outline map. // line 55 float2 uv_outline_base = colorUV + unitCircle / 8.0; // * interesting objects (circle) float2 uv_outline_interesting_circle = uv_outline_base * 0.5; float outline_interesting_circle = texture2.Sample( sampler2, uv_outline_interesting_circle ).x; outlineInteresting += outline_interesting_circle / 8.0; // * traces (circle) float2 uv_outline_traces_circle = uv_outline_base * 0.5 + float2(0.5, 0.0); float outline_traces_circle = texture2.Sample( sampler2, uv_outline_traces_circle ).x; outlineTraces += outline_traces_circle / 8.0; // * sample color texture (zooming effect) with perturbation float2 uv_color_circle = colorUV + unitCircle * offsetUV; float3 color_circle = texture0.Sample( sampler0, uv_color_circle ).rgb; color_circle_main += color_circle / 8.0; } Color sampling is almost the same, but we add an offset multiplied by the “single” circle to the base colorUV .
Brightness
After the loop, we sample the brightness map and change the final brightness values (because the brightness map knows nothing about the contours):
67: sample_indexable(texture2d)(float,float,float,float) r0.xy, r1.zwzz, t3.xyzw, s0 68: mad_sat r0.xy, -r0.xyxx, l(0.800000, 0.750000, 0.000000, 0.000000), r4.xyxx HLSL code:
// * Sample intensity map float2 intensityMap = texture3.Sample( sampler0, colorUV ).xy; float intensityInteresting = intensityMap.r; float intensityTraces = intensityMap.g; // * Adjust outlines float mainOutlineInteresting = saturate( outlineInteresting - 0.8*intensityInteresting ); float mainOutlineTraces = saturate( outlineTraces - 0.75*intensityTraces ); Gray corners and the final union of all
Gray color closer to the corners is calculated using dot-product (assembly line 69):
// * Greyish color float3 color_greyish = dot( color_circle_main, float3(0.3, 0.3, 0.3) ).xxx; 
Then there are two interpolations. The first combines gray with “color in a circle” using the first mask I described, so the corners become gray. In addition, there is a coefficient of 0.6, which reduces the saturation of the final image:

The second combines the first color with the one above using fisheyeAmount . This means that the screen becomes gradually darker (due to multiplication by 0.6) and grayer in the corners! Brilliant.
HLSL:
// * Determine main color. // (1) At first, combine "circled" color with gray one. // Now we have have greyish corners here. float3 mainColor = lerp( color_greyish, color_circle_main, mask_gray_corners ) * 0.6; // (2) Then mix "regular" color with the above. // Please note this operation makes corners gradually gray (because fisheyeAmount rises from 0 to 1) // and gradually darker (because of 0.6 multiplier). mainColor = lerp( color, mainColor, fisheyeAmount ); Now we can proceed to adding contours of objects.
Colors (red and yellow) are taken from the buffer constants.
// * Determine color of witcher senses float3 senses_traces = mainOutlineTraces * colorTraces; float3 senses_interesting = mainOutlineInteresting * colorInteresting; float3 senses_total = 1.2 * senses_traces + senses_interesting; 
Fuh! We are almost at the finish line!
We have the final color, there is the color of witch's flair ... it remains to somehow combine them!
And for this, simple addition is not suitable. First we calculate the scalar product:
78: dp3_sat r0.x, r0.xyzx, l(1.000000, 1.000000, 1.000000, 0.000000) float dot_senses_total = saturate( dot(senses_total, float3(1.0, 1.0, 1.0) ) ); which looks like this:

And these values at the very end are used for interpolation between color and (saturated) witcher's grip:
76: mad r0.xyz, r0.yzwy, l(1.200000, 1.200000, 1.200000, 0.000000), r2.xyzx 77: mov_sat r2.xyz, r0.xyzx 78: dp3_sat r0.x, r0.xyzx, l(1.000000, 1.000000, 1.000000, 0.000000) 79: add r0.yzw, -r1.xxyz, r2.xxyz 80: mad o0.xyz, r0.xxxx, r0.yzwy, r1.xyzx 81: mov o0.w, l(1.000000) 82: ret float3 senses_total = 1.2 * senses_traces + senses_interesting; // * Final combining float3 senses_total_sat = saturate(senses_total); float dot_senses_total = saturate( dot(senses_total, float3(1.0, 1.0, 1.0) ) ); float3 finalColor = lerp( mainColor, senses_total_sat, dot_senses_total ); return float4( finalColor, 1.0 ); 
And that is all.
Full shader posted here .
Comparison of my (left) and original (right) shaders:
Hope you enjoyed this article! There are many brilliant ideas in the mechanics of the “witcher's instinct”, and the final result is very plausible.
[The previous parts of the analysis: the first and second .]
Source: https://habr.com/ru/post/450332/
All Articles