Why software tasks always take longer than you think
Everyone in the IT industry knows how difficult it is to assess the duration of a project. It is difficult to objectively estimate how long it will take to solve a difficult problem. One of my favorite theories is that it’s just a statistical artifact.
Suppose you rate a project at 1 week. Suppose there are three equally likely results: either it takes 1/2 week, or 1 week, or 2 weeks. The median result is actually the same as the assessment: 1 week, but the average value (aka average, aka expected value) is 7/6 = 1.17 weeks. The estimate is actually calibrated (impartial) for the median (which is equal to 1), but not for the average.
A reasonable model for the “inflation factor” (actual time divided by estimated time) will be something like a lognormal distribution . If the estimate is equal to one week, then we will model the real result as a random variable distributed in accordance with a lognormal distribution of about one week. In this situation, the median of the distribution is exactly one week, but the average is much larger:

')
If we take the logarithm of the inflation rate, we get a simple normal distribution with center about 0. This implies a median inflation rate of 1x, and, as you hopefully remember, log (1) = 0. However, in various problems there can be different uncertainties around 0. We can model them by changing the parameter σ, which corresponds to the standard deviation of the normal distribution:
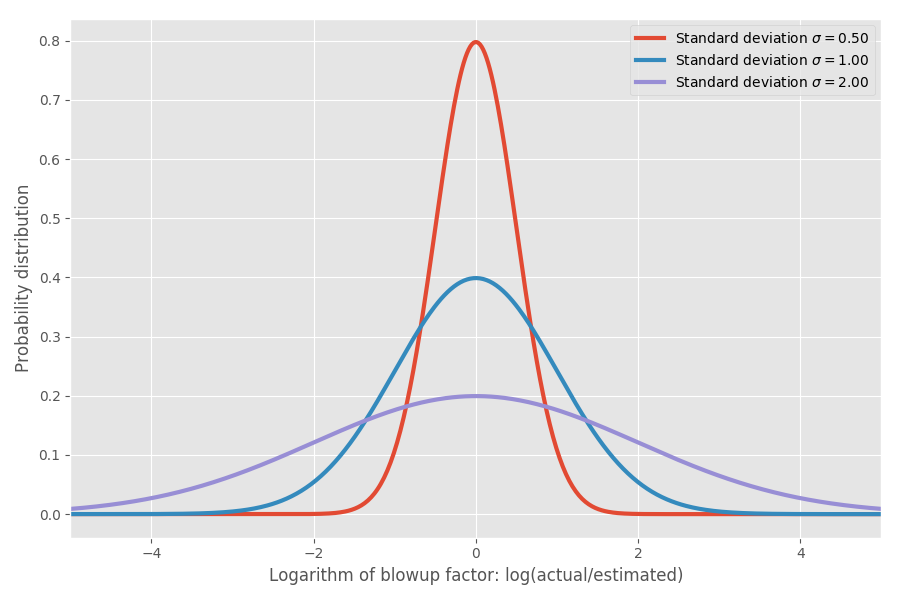
Just to show real numbers: when log (actual / estimated) = 1, then the inflation coefficient exp (1) = e = 2.72. It is equally likely that the project will stretch in exp (2) = 7.4 times, and that it will end in exp (-2) = 0.14, that is, in 14% of the estimated time. Intuitively, the reason why the average is so high is that tasks that are performed faster than expected cannot compensate for tasks that take much longer than expected. We are limited to 0, but not limited in the other direction.
Is it just a model? Still would! But soon I will get to the real data and on some empirical data I will show that in fact it corresponds well enough to reality.
So far so good, but let's really try to understand what this means in terms of estimating the timing of software development. Suppose we look at a plan of 20 different software projects and try to estimate how long it will take to complete them all .
This is where the middle becomes decisive. The averages are added, but there are no medians. Therefore, if we want to get an idea of how long it will take to complete the sum of N projects, we need to look at the average value. Suppose we have three different projects with the same σ = 1:
Note that the averages add up and 4.95 = 1.65 * 3, but other columns do not.
Now we add three projects with different sigmas:
The averages still add up, but the reality is not even close to the naive estimate of 3 weeks, which you could have imagined. Note that a highly uncertain project with σ = 2 dominates over the others on average completion time. And for the 99th percentile, it not only dominates, but literally absorbs all the others. We can give an example more .:
Again, the only unpleasant task mainly dominates the estimation calculations, at least in 99% of cases. Even in average time, one crazy project ultimately takes about half the time spent on all tasks, although the median has similar values. For simplicity, I assumed that all tasks have the same time estimate, but different uncertainties. Mathematics is saved when you change the timing.
It's funny, but I have a feeling for a long time. Adding ratings rarely works when you have a lot of tasks. Instead, find out which tasks have the highest uncertainty: these tasks will usually dominate on average the execution time.
The diagram shows the mean and 99th percentile as a function of uncertainty (σ):
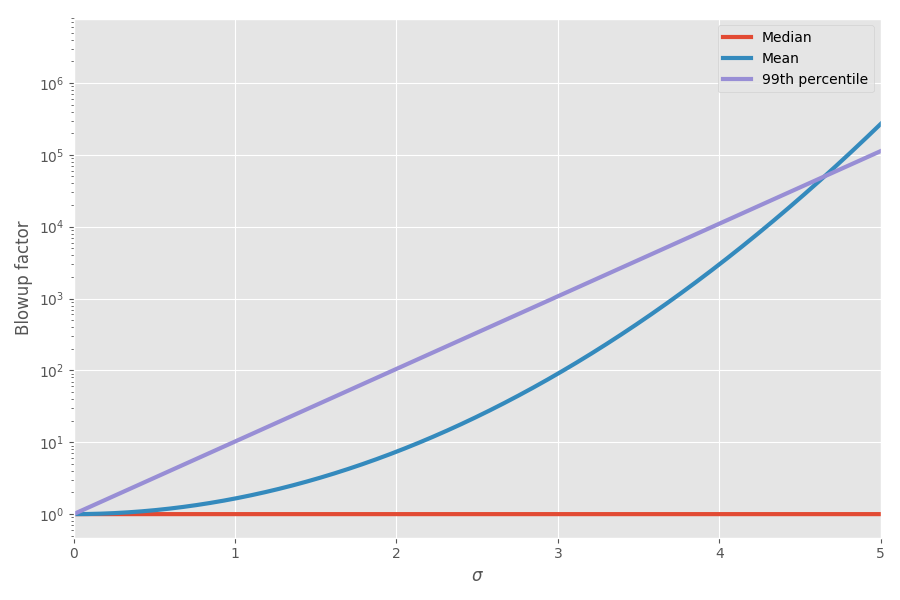
Now math explained my feelings! I started to take this into account when planning projects. I really think that adding estimates to the deadlines for completing tasks is very misleading and creates a false picture of how long the project will take entirely, because you have these crazy skewed tasks that ultimately take up all the time.
For a long time I kept it in the brain in the section “curious toy models”, sometimes thinking that this is a neat illustration of the phenomenon of the real world. But one day, wandering around the network, I came across an interesting set of data on estimating the timing of projects and the actual time they were completed. Fantasy!
Let's make a quick scatter plot of estimated and actual time:
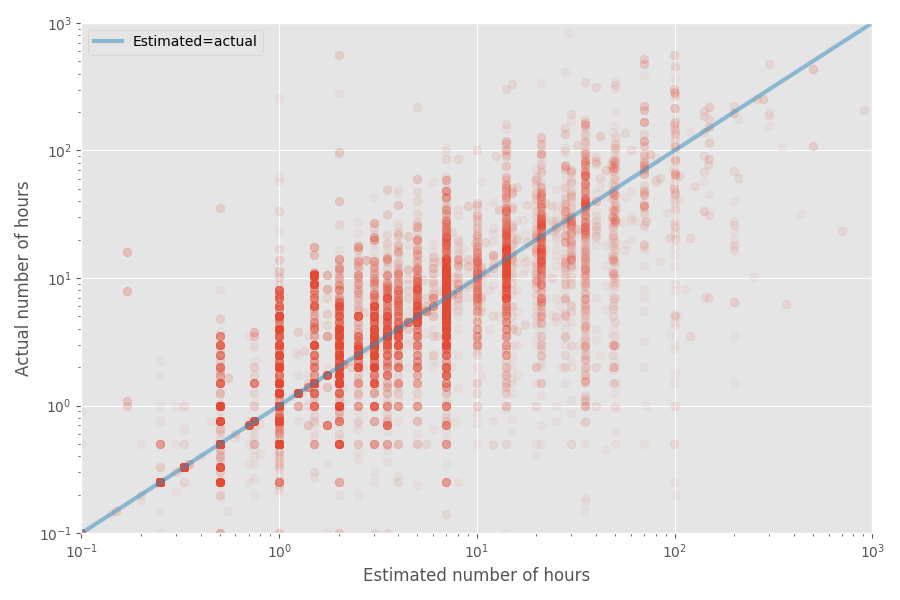
The median inflation rate for this dataset is 1X, while the average coefficient is 1.81x. Again, this confirms the conjecture that developers are well aware of the median, but the average is much higher.
Let's look at the distribution of the coefficient of inflation (logarithm):
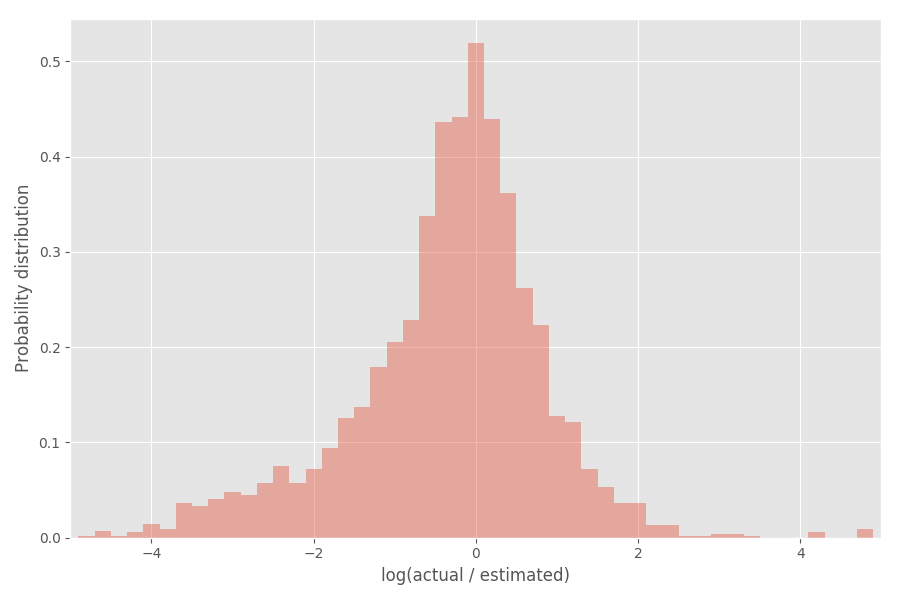
As you can see, it is fairly well centered around 0, where the inflation coefficient is exp (0) = 1.
Now I'm going to fantasize a bit with statistics - feel free to skip this part if you are not interested. What can we conclude from this empirical distribution? You can expect that the logarithms of the inflation rate will be distributed according to the normal distribution, but this is not exactly the case. Note that the σ themselves are random and vary for each project.
One of the convenient ways to simulate σ is that they are selected from the inverse gamma distribution . If we assume (as before) that the logarithm of inflation coefficients is distributed in accordance with the normal distribution, then the “global” distribution of the logarithms of inflation rates ends with the Student’s distribution .
Apply the distribution of student on the previous:

Decently converges, in my opinion! Student’s distribution parameters also determine the inverse gamma distribution of σ values:
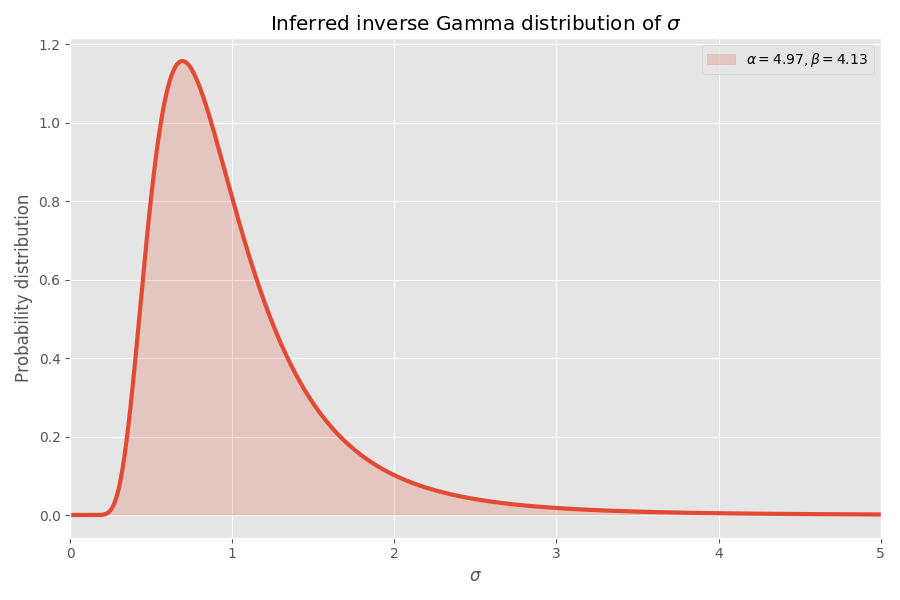
Note that the values of σ> 4 are very unlikely, but when they occur, they cause an average explosion several thousand times.
Assuming that this data set is representative of software development (it is doubtful!), We can draw a few more conclusions. We have parameters for Student’s distribution, so we can calculate the average time it takes to complete a task without knowing σ for this task.
While the median inflation rate of this fit is 1x (as before), the 99% inflation rate is 32x, but if you go to the 99.99th percentile, that's a whopping 55 million ! One (free) interpretation is that some tasks are almost impossible in the end. In fact, these very extreme cases have such a huge impact on the average that the average inflation rate of any task becomes infinite . This is pretty bad news for those who are trying to meet deadlines!
If my model is correct (great if), then this is what we can find out:
Suppose you rate a project at 1 week. Suppose there are three equally likely results: either it takes 1/2 week, or 1 week, or 2 weeks. The median result is actually the same as the assessment: 1 week, but the average value (aka average, aka expected value) is 7/6 = 1.17 weeks. The estimate is actually calibrated (impartial) for the median (which is equal to 1), but not for the average.
A reasonable model for the “inflation factor” (actual time divided by estimated time) will be something like a lognormal distribution . If the estimate is equal to one week, then we will model the real result as a random variable distributed in accordance with a lognormal distribution of about one week. In this situation, the median of the distribution is exactly one week, but the average is much larger:

')
If we take the logarithm of the inflation rate, we get a simple normal distribution with center about 0. This implies a median inflation rate of 1x, and, as you hopefully remember, log (1) = 0. However, in various problems there can be different uncertainties around 0. We can model them by changing the parameter σ, which corresponds to the standard deviation of the normal distribution:

Just to show real numbers: when log (actual / estimated) = 1, then the inflation coefficient exp (1) = e = 2.72. It is equally likely that the project will stretch in exp (2) = 7.4 times, and that it will end in exp (-2) = 0.14, that is, in 14% of the estimated time. Intuitively, the reason why the average is so high is that tasks that are performed faster than expected cannot compensate for tasks that take much longer than expected. We are limited to 0, but not limited in the other direction.
Is it just a model? Still would! But soon I will get to the real data and on some empirical data I will show that in fact it corresponds well enough to reality.
Estimation of software development terms
So far so good, but let's really try to understand what this means in terms of estimating the timing of software development. Suppose we look at a plan of 20 different software projects and try to estimate how long it will take to complete them all .
This is where the middle becomes decisive. The averages are added, but there are no medians. Therefore, if we want to get an idea of how long it will take to complete the sum of N projects, we need to look at the average value. Suppose we have three different projects with the same σ = 1:
| Median | The average | 99% | |
|---|---|---|---|
| Task A | 1.00 | 1.65 | 10.24 |
| Task B | 1.00 | 1.65 | 10.24 |
| Task C | 1.00 | 1.65 | 10.24 |
| SUM | 3.98 | 4.95 | 18.85 |
Note that the averages add up and 4.95 = 1.65 * 3, but other columns do not.
Now we add three projects with different sigmas:
| Median | The average | 99% | |
|---|---|---|---|
| Problem A (σ = 0.5) | 1.00 | 1.13 | 3.20 |
| Problem B (σ = 1) | 1.00 | 1.65 | 10.24 |
| Problem C (σ = 2) | 1.00 | 7.39 | 104.87 |
| SUM | 4.00 | 10.18 | 107.99 |
The averages still add up, but the reality is not even close to the naive estimate of 3 weeks, which you could have imagined. Note that a highly uncertain project with σ = 2 dominates over the others on average completion time. And for the 99th percentile, it not only dominates, but literally absorbs all the others. We can give an example more .:
| Median | The average | 99% | |
|---|---|---|---|
| Problem A (σ = 0.5) | 1.00 | 1.13 | 3.20 |
| Problem B (σ = 0.5) | 1.00 | 1.13 | 3.20 |
| Problem C (σ = 0.5) | 1.00 | 1.13 | 3.20 |
| Problem D (σ = 1) | 1.00 | 1.65 | 10.24 |
| Problem E (σ = 1) | 1.00 | 1.65 | 10.24 |
| Problem F (σ = 1) | 1.00 | 1.65 | 10.24 |
| Problem G (σ = 2) | 1.00 | 7.39 | 104.87 |
| SUM | 9.74 | 15.71 | 112.65 |
Again, the only unpleasant task mainly dominates the estimation calculations, at least in 99% of cases. Even in average time, one crazy project ultimately takes about half the time spent on all tasks, although the median has similar values. For simplicity, I assumed that all tasks have the same time estimate, but different uncertainties. Mathematics is saved when you change the timing.
It's funny, but I have a feeling for a long time. Adding ratings rarely works when you have a lot of tasks. Instead, find out which tasks have the highest uncertainty: these tasks will usually dominate on average the execution time.
The diagram shows the mean and 99th percentile as a function of uncertainty (σ):

Now math explained my feelings! I started to take this into account when planning projects. I really think that adding estimates to the deadlines for completing tasks is very misleading and creates a false picture of how long the project will take entirely, because you have these crazy skewed tasks that ultimately take up all the time.
Where is the empirical evidence?
For a long time I kept it in the brain in the section “curious toy models”, sometimes thinking that this is a neat illustration of the phenomenon of the real world. But one day, wandering around the network, I came across an interesting set of data on estimating the timing of projects and the actual time they were completed. Fantasy!
Let's make a quick scatter plot of estimated and actual time:

The median inflation rate for this dataset is 1X, while the average coefficient is 1.81x. Again, this confirms the conjecture that developers are well aware of the median, but the average is much higher.
Let's look at the distribution of the coefficient of inflation (logarithm):

As you can see, it is fairly well centered around 0, where the inflation coefficient is exp (0) = 1.
Take statistical tools
Now I'm going to fantasize a bit with statistics - feel free to skip this part if you are not interested. What can we conclude from this empirical distribution? You can expect that the logarithms of the inflation rate will be distributed according to the normal distribution, but this is not exactly the case. Note that the σ themselves are random and vary for each project.
One of the convenient ways to simulate σ is that they are selected from the inverse gamma distribution . If we assume (as before) that the logarithm of inflation coefficients is distributed in accordance with the normal distribution, then the “global” distribution of the logarithms of inflation rates ends with the Student’s distribution .
Apply the distribution of student on the previous:

Decently converges, in my opinion! Student’s distribution parameters also determine the inverse gamma distribution of σ values:

Note that the values of σ> 4 are very unlikely, but when they occur, they cause an average explosion several thousand times.
Why software tasks always take longer than you think
Assuming that this data set is representative of software development (it is doubtful!), We can draw a few more conclusions. We have parameters for Student’s distribution, so we can calculate the average time it takes to complete a task without knowing σ for this task.
While the median inflation rate of this fit is 1x (as before), the 99% inflation rate is 32x, but if you go to the 99.99th percentile, that's a whopping 55 million ! One (free) interpretation is that some tasks are almost impossible in the end. In fact, these very extreme cases have such a huge impact on the average that the average inflation rate of any task becomes infinite . This is pretty bad news for those who are trying to meet deadlines!
Summary
If my model is correct (great if), then this is what we can find out:
- People appreciate the median task time, but not the average.
- The average time is much longer than the median because the distribution is distorted (lognormal distribution).
- When you add estimates for n problems, things get worse.
- The tasks of greatest uncertainty (rather, the largest size) can often dominate the average time required to complete all tasks.
- The average time to complete a task that we know nothing about is actually infinite .
Notes
- Obviously, the conclusions are based on only one data set, which I found on the Internet. Other data sets may give different results.
- My model, of course, is also very subjective, like any statistical model.
- I would be happy to apply the model to a much larger set of data to see how stable it is.
- I assumed that all tasks are independent. In fact, they may have a correlation, which will make the analysis much more annoying, but (I think) end up with similar conclusions.
- The sum of lognormally distributed values is not another lognormally distributed value. This is a weakness of this distribution, since you can argue that most tasks are simply the sum of subtasks. It would be nice if our distribution was sustainable .
- I deleted small tasks from the histogram (the estimated time is less than or equal to 7 hours), since they distort the analysis and there was a strange surge at exactly 7.
- The code is on Github , as usual.
Source: https://habr.com/ru/post/449678/
All Articles