Create from scratch your own neural network in Python

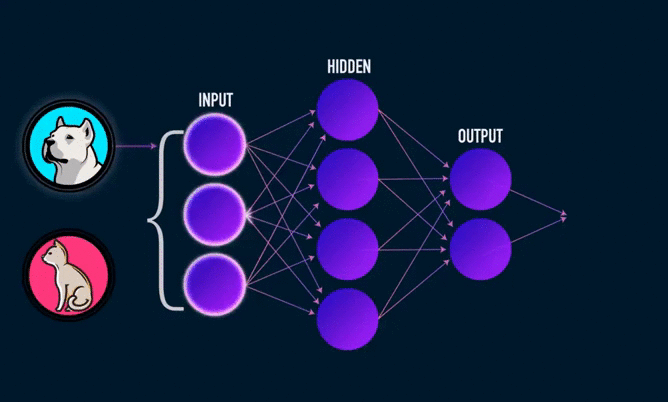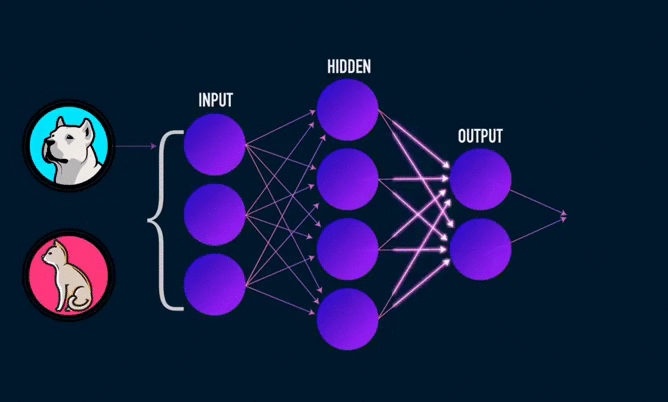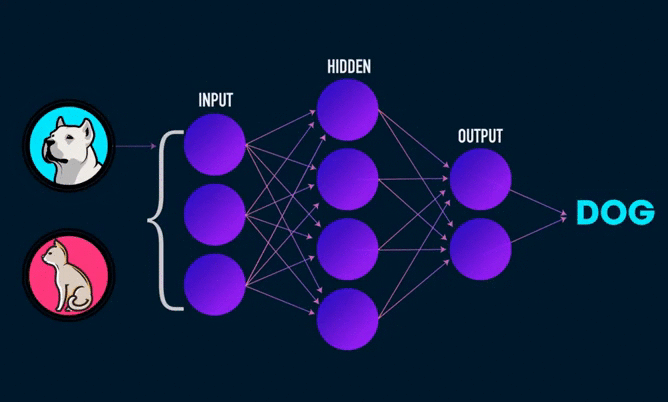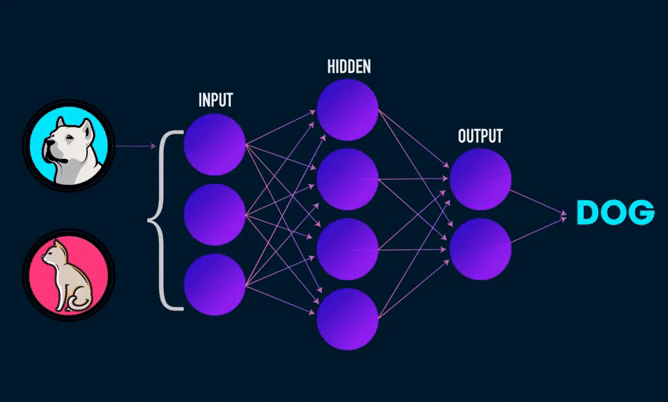
Hello! An interesting topic is on the agenda - we will create our own neural network in Python from scratch. At its core, we manage without complex libraries ( TensorFlow and Keras ).

The main thing you need to know is that an artificial neural network can be represented in the form of blocks / circles (artificial neurons) that have connections with each other, in a certain direction. In the operation of a biological neural network, an electrical signal is transmitted from the network inputs to the outputs (it may change during the passage).


')
Electrical signals in the connections of an artificial neural network are numbers . We will give random numbers to the inputs of our artificial neural network (which would symbolize the magnitude of the electrical signal, if it were). These numbers, moving along the network will in some way change. At the output, we get the answer to our network in the form of a number.

Artificial neuron

In order for us to understand how the neural network works from the inside, we will carefully study the model of an artificial neuron:



Random numbers entering the input are multiplied by their weights. First input signal $$$X_1$Multiplied by the weight corresponding to this input $$$w_1$. As a result, we get $$$X_1 w_1$. And so on $$$n$-Th entry. As a result, at the last entry we get $$$x_n w_n$.

After that, all works are transmitted to the adder, which summarizes all input numbers multiplied by the corresponding weights:

$$$x_1w_1 + x_2w_2 + \ cdots + x_nw_n = \ sum \ limits ^ n_ {i = 1} x_iw_i$

Help on Sigma.

The result of the adder is a number called a weighted sum :

$$$net = \ sum \ limits ^ n_ {i = 1} x_iw_i$

I note that it is pointless to just give a weighted amount to the output. The neuron must process it and get an adequate output signal. For these purposes, use the activation function (we will use Sigmoid).

Activation function $$$(Φ (net))$- A function that takes a weighted sum as an argument. The value of this function is the output of the neuron. $$$(Out)$.

Neural network training

Neural network training is a process of fine-tuning scales and offsets from the input data. Of course, the correct values ​​for weights and offsets determine the accuracy of the predictions.

The output of the two-layer neural network will be as follows:

$$$ inline $ ŷ = σ (W_2σ (W_1x + b_1) + b_2) $ inline $

$$$x$- input layer;
$$$ŷ$- output layer;
$$$W$- a set of scales;
$$$b$- set of offsets;
$$$σ$- selection of an activation function for each hidden layer.

How do we see the weight $$$W$and offsets $$$b$are the only variables that affect the output $$$ŷ$.

For information, the result of re-applying the learning process consists of 2 steps:

• Calculate predicted output $$$ŷ$;
• Updating weights and offsets.

We describe all this in the code:

class NeuralNetwork: def __init__(self, x, y): self.input = x self.weights1 = np.random.rand(self.input.shape[1],4) self.weights2 = np.random.rand(4,1) self.y = y self.output = np.zeros(self.y.shape) def feedforward(self): self.layer1 = sigmoid(np.dot(self.input, self.weights1)) self.output = sigmoid(np.dot(self.layer1, self.weights2)) 

We will evaluate the quality of our results (a set of weights and offsets, which minimizes the loss function) together with the sum of the squares of errors (the average value of the difference between each predicted and actual value):

$$$Sum - of- Squares Error = \ sum \ limits ^ n_ {i = 1} (y-ŷ) ^ 2$

Next, after measuring the error of our prediction, we need to find a way to propagate the error back and update our weights and offsets. This will help us gradient descent .

Here we will not be able to calculate the loss functions with respect to weights and displacements, since its equation does not contain weights and displacements.

Hooray! We got what we need - the derivative of the loss function with respect to the weights. Now we can adjust the weight.

Add the backpropagation function to our code:

 class NeuralNetwork: def __init__(self, x, y): self.input = x self.weights1 = np.random.rand(self.input.shape[1],4) self.weights2 = np.random.rand(4,1) self.y = y self.output = np.zeros(self.y.shape) def feedforward(self): self.layer1 = sigmoid(np.dot(self.input, self.weights1)) self.output = sigmoid(np.dot(self.layer1, self.weights2)) def backprop(self): d_weights2 = np.dot(self.layer1.T, (2*(self.y - self.output) * sigmoid_derivative(self.output))) d_weights1 = np.dot(self.input.T, (np.dot(2*(self.y - self.output) * sigmoid_derivative(self.output), self.weights2.T) * sigmoid_derivative(self.layer1))) self.weights1 += d_weights1 self.weights2 += d_weights2 

On this, our network is ready. I propose to draw conclusions on the quality of the neural network for everyone.

All knowledge!



More detailed articles in the Neuron telegram channel (@neurondata), do not miss interesting posts.