Universal and perfect hashing
We start the week with useful material dedicated to the launch of the course "Algorithms for Developers" . Enjoy your reading.

1. Overview
')
Hashing is a great practical tool, with an interesting and subtle theory. In addition to being used as a vocabulary data structure, hashing is also found in many different areas, including cryptography and complexity theory. In this lecture, we describe two important concepts: universal hashing (also known as universal families of hash functions) and perfect hashing.
The material covered in this lecture includes:
2. Introduction
We will look at the main problem with the dictionary that we discussed before and consider two versions: static and dynamic:
For the first problem, we could use a sorted array and a binary search. For the second, we could use a balanced search tree. However, hashing provides an alternative approach, which is often the fastest and most convenient way to solve these problems. For example, suppose you are writing a program for an AI search and want to store situations that you have already resolved (positions on the board or elements of the state space), so as not to repeat the same calculations when encountering them again. Hashing provides an easy way to store such information. There are also many applications in cryptography, networks, complexity theory.
3. Basics of Hashing
The formal setting for hashing is as follows.
One of the remarkable properties of hashing is that all dictionary operations are incredibly simple to implement. To search for the key x, simply calculate the index i = h (x) and then go through the list in A [i] until you find it (or leave the list). To insert, simply place a new item at the top of its list. To delete, you just need to perform the delete operation in the linked list. Now we come to the question: what do we need to achieve good performance?
Desirable properties. The main desirable properties for a good hashing scheme:
Given this, the search time for the element x is O (the list size is A [h (x)]). The same is true for deletions. Inserts take O (1) time, regardless of the length of the lists. So we want to analyze how big these lists are.
Basic intuition: one of the ways to distribute elements beautifully is to distribute them randomly. Unfortunately, we cannot simply use a random number generator to decide where to send the next element, because then we can never find it again. So, we want h to be something “pseudo-random” in some formal sense.
We will now set out some bad news, and then some good news.
Statement 1 (Bad News) For any hash function h, if | U | ≥ (N −1) M +1, there is a set S of N elements that are all hashed in one place.
Proof: according to the Dirichlet principle. In particular, to consider the contraposition, if each location had at most N - 1 U elements hashing it, then U could have a size of at most M (N - 1).
This is partly why hashing seems so mysterious - how can you say that hashing is good, if for any hash function you can think of ways to prevent it? One answer is that there are a lot of simple hash functions that work well in practice for typical sets S. But what if we want to get a good guarantee of the worst case?
Here's the key idea: let's use randomization in our design h, by analogy with the randomized quick sort. (Needless to say, h is a deterministic function). We show that for any sequence of insertion and search operations (we do not need to assume that the set of inserted elements of S is random), if we choose h in this probabilistic way, the performance of h in this sequence will be good in waiting. Thus, this is the same guarantee as in randomized quicksort or traps. In particular, this is the idea of universal hashing.
As soon as we develop this idea, we will use it for a particularly nice application called “perfect hashing”.
4. Universal hashing
Definition 1. Randomized algorithm H for constructing hash functions h: U → {1, ..., M}
is universal if for all x! = y in U we have
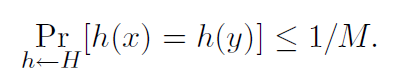
We can also say that the set H of hash functions is a universal family of hash functions, if the procedure “choose h ∈ H at random” is universal. (Here we identify a set of functions with a uniform distribution over the set.)
Theorem 2. If H is universal, then for any set S ⊆ U of size N, for any x ∈ U (for example, which we could look for), if we build h randomly according to H, the expected number of collisions between x and others elements in S no more than N / M.
Proof: every y ∈ S (y! = X) has no more than 1 / M chance of colliding with x by the definition of “universal”. So,
Now we get the following corollary.
Corollary 3. If H is universal, then for any sequence of operations L insert, search and delete, in which there can be no more than M elements in the system at the same time, the expected total cost of L operations for random h ∈ H is equal to O (L) (viewing time to calculate h as a constant).
Proof: for any given operation in sequence, its expected cost is constant by Theorem 2, therefore the expected total cost of L operations is O (L) in linearity of expectation.
The question is: can we actually build a universal H? If not, then this is all pretty pointless. Fortunately, the answer is yes.
4.1. Creating a universal hash family: matrix method
Suppose the keys are u-bit in length. Say, the size of the table M is equal to degree 2, so the index is the length of b-bits with M = 2b.
What we will do is choose h as the random matrix 0/1 b-by-u and define h (x) = hx, where we add mod 2. These matrices are short and thick. For example:
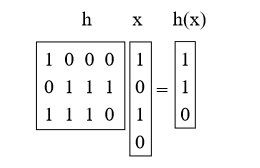
Statement 4. For x! = Y, Prh [h (x) = h (y)] = 1 / M = 1 / 2b.
Proof: First, what does multiplying h by x mean? We can think of this as adding some of the columns of h (doing vector addition mod 2), where 1 bit in x indicates which ones to add. (for example, we added the 1st and 3rd columns h above)
Now take an arbitrary pair of keys x, y such that x! = Y. They should differ somewhere, so, let's say, they differ in the i-th coordinate, and for concreteness, say xi = 0 and yi = 1. Imagine that first we chose all h except the i-th column. For the remaining samples of the ith column, h (x) is fixed. However, each of the 2b different settings of the i-th column gives a different value of h (y) (in particular, each time we turn a bit in this column, we turn the corresponding bit in h (y)). Thus, there is exactly a 1 / 2b chance that h (x) = h (y).
There are other methods for constructing universal hash families, also based on multiplying prime numbers (see Section 6.1).
The next question we will consider is: if we correct the set S, can we find the hash function h such that all searches will have constant time? The answer is yes, and this leads to the topic of perfect hashing.
5. Perfect hashing
We say that the hash function is ideal for S if all searches occur in O (1). Here are two ways to build perfect hash functions for a given set of S.
5.1 Method 1: Solution in O (N2) space
Let's say we want to have a table whose size is quadratic in size N of our dictionary S. Then here is a simple method for constructing an ideal hash function. Let H be universal and M = N2. Then just choose a random h from H and try it! The assertion is that there is at least a 50% chance that she will not have collisions.
Proposition 5. If H is universal and M = N2, then Prh∼H (no collisions in S) ≥ 1/2.
Evidence:
• How many pairs (x, y) are there in S? Answer:
• For each pair, the probability of their collision is ≤ 1 / M by definition universality.
• So, Pr (there is a collision) ≤ / M <1/2.
/ M <1/2.
It’s like the other side of the “birthday paradox”. If the number of days is much more than the number of people in the square, then there is a reasonable chance that no couple will have the same birthday.
So, we just choose a random h from H, and if there are any collisions, we simply choose a new h. On average, we only need to do this twice. Now, what if we want to use only the O (N) space?
5.2 Method 2: Solution in O (N) space
The question of whether you can achieve perfect hashing in O (N) space has been open for some time: “Should the tables be sorted?”. That is, for a fixed set, you can get a constant search time only with linear space? There was a series of more and more complex attempts, until finally it was solved using the good idea of universal hash functions in a two-level scheme.
The method consists in the following. First we will hash into a table of size N using universal hashing. This will lead to some collisions (unless we are lucky). However, then we rehash each basket using method 1, squaring the size of the basket to get zero collisions. Thus, the scheme is that we have the first level hash function h and the first level table A, and then the second level N hash functions h1, ..., hN and N of the second level table A1, ..., A.N ... To find the element x, we first calculate i = h (x), and then find the element in Ai [hi (x)]. (If you did this in practice, you could set the flag so that you take the second step only if there were actually collisions with the index i, and otherwise you would just put x in A [i], but let's let's not worry about it here.)
Say, the hash function h hashes n elements S to location i. We have already proved (by analyzing method 1) that we can find h1, ..., hN, so that the total space used in the secondary tables is Pi (ni) 2. It remains to show that we can find a first-level function h such that Pi (ni) 2 = O (N). In fact, we show the following:
Theorem 6. If we choose the starting point h from the universal set H, then
Evidence. We prove this by showing that E [Pi (ni) 2] <2N. This implies what we want from Markov's inequality. (If there was even a probability of 1/2 that the amount could be more than 4N, then this fact in itself would mean that the expectation should have been more than 2N. Thus, if the expectation is less than 2N, the probability of failure should be less 1/2.)
Now, the tricky trick is that one of the ways to calculate this number is to count the number of ordered pairs that have collisions, including collisions with themselves. For example, if the basket has {d, e, f}, then d will have a collision with each of {d, e, f}, e will have a collision with each of {d, e, f}, and f will have a conflict with each of {d, e, f}, so we get 9. So, we have:
So, we simply try a random h from H until we find such that Pi n2 i <4N, and then, fixing this function h, we find N secondary hash functions h1, ..., hN as in method 1.
6. Further discussion
6.1 Another universal hashing method
Here is another method for constructing universal hash functions, which is slightly more efficient than the matrix method given earlier.
In the matrix method, we considered the key as a vector of bits. In this method, instead, we will consider the key x as a vector of integers [x1, x2, ..., xk] with the only requirement that each xi be in the range {0, 1, ..., M-1}. For example, if we hash strings of length k, then xi may be the i-th character (if the size of our table is at least 256) or the i-th pair of characters (if the size of our table is at least 65536). In addition, we will require that the size of our table M is a prime number. To choose the hash function h, we will select k random numbers r1, r2, ..., pk from {0, 1, ..., M - 1} and determine:
The proof that this method is universal is constructed in the same way as the proof of the matrix method. Let x and y be two different keys. We want to show that Prh (h (x) = h (y)) ≤ 1 / M. Since x! = Y, there must be a case when there exists some index i such that xi! = Yi. Now imagine that you first selected all random numbers rj for j! = I. Let h ′ (x) = Pj6 = i rjxj. So, choosing ri, we get h (x) = h ′ (x) + rixi. This means that we have a collision between x and y precisely when
Since M is simple, division by a non-zero value mod M is valid (every integer from 1 to M −1 has a multiplicative inverse modulo M), which means that there is exactly one value ri modulo M for which the above equation true, namely ri = (h (y) - h (x)) / (xi - yi) mod M. Thus, the probability of this occurrence is exactly 1 / M.
6.2 Other uses of hashing
Suppose we have a long sequence of elements, and we want to see how many different elements are in the list. Is there a good way to do this?
One way is to create a hash table, and then make one pass through the sequence, making a search for each element and then inserting it if it is not already in the table. The number of individual elements is simply the number of inserts.
And now that if the list is really huge and we do not have a place to store it, but an approximate answer will suit us. For example, imagine that we are a router and observe how many packets pass, and we want (approximately) to see how many different source IP addresses exist.
Here's a good idea: let's say we have a hash function h, which behaves like a random function, and let's imagine that h (x) is a real number from 0 to 1. One thing we can do is just keep track of the minimum The hash cost has been generated so far (so we won't have a table at all). For example, if the keys are 3, 10, 3, 3, 12, 10, 12 and h (3) = 0.4, h (10) = 0.2, h (12) = 0.7, then we get 0, 2
The fact is that if we choose N random numbers in [0, 1], the expected minimum value will be 1 / (N + 1). In addition, there is a good chance that it is pretty close (we can improve our estimate by running several hash functions and taking the median of the minima).
Question: why use a hash function, and not just choose a random number every time? This is because we care about the number of different elements, not just the total number of elements (the problem is much simpler: just use the counter ...).
Friends, was this article helpful to you? Write in the comments and join the open day , which will be held on April 25th.

1. Overview
')
Hashing is a great practical tool, with an interesting and subtle theory. In addition to being used as a vocabulary data structure, hashing is also found in many different areas, including cryptography and complexity theory. In this lecture, we describe two important concepts: universal hashing (also known as universal families of hash functions) and perfect hashing.
The material covered in this lecture includes:
- Formal statement and general idea of hashing.
- Universal hashing.
- Perfect hashing.
2. Introduction
We will look at the main problem with the dictionary that we discussed before and consider two versions: static and dynamic:
- Static : given the many elements of S, we want to store it in such a way that you can quickly perform a search.
- For example, a fixed dictionary.
- Dynamic : here we have a sequence of requests for insertion, search, and possibly deletion. We want to do it all efficiently.
For the first problem, we could use a sorted array and a binary search. For the second, we could use a balanced search tree. However, hashing provides an alternative approach, which is often the fastest and most convenient way to solve these problems. For example, suppose you are writing a program for an AI search and want to store situations that you have already resolved (positions on the board or elements of the state space), so as not to repeat the same calculations when encountering them again. Hashing provides an easy way to store such information. There are also many applications in cryptography, networks, complexity theory.
3. Basics of Hashing
The formal setting for hashing is as follows.
- The keys belong to some large set of U. (For example, imagine that U is a set of all strings with a length of no more than 80 ascii characters.)
- There are some set of keys S in U, which we actually need (the keys can be both static and dynamic). Let N = | S |. Imagine that N is much smaller than the size of U. For example, S is the set of names of students in a class that is much smaller than 12880.
- We will perform inserts and search using an array A of some size M and a hash function h: U → {0, ..., M - 1}. Given an element x, the idea of hashing is that we want to store it in A [h (x)]. Note that if U were small (for example, 2-character strings), then you could just save x to A [x], as in block sorting. The problem is that U is big, so we need a hash function.
- We need a method for resolving collisions. A collision is when h (x) = h (y) for two different keys x and y. In this chapter, we will handle collisions by defining each element of A as a linked list. There are a number of other methods, but for the problems that we focus on here, this is the most suitable. This method is called the chain method. To insert an item, we simply place it at the top of the list. If h is a good hash function, then we hope that the lists will be small.
One of the remarkable properties of hashing is that all dictionary operations are incredibly simple to implement. To search for the key x, simply calculate the index i = h (x) and then go through the list in A [i] until you find it (or leave the list). To insert, simply place a new item at the top of its list. To delete, you just need to perform the delete operation in the linked list. Now we come to the question: what do we need to achieve good performance?
Desirable properties. The main desirable properties for a good hashing scheme:
- The keys are well spread out so that we do not have too many collisions, since collisions affect the time it takes to perform a search and delete.
- M = O (N): in particular, we would like our scheme to reach property (1) without the need for the table size M to be much larger than the number of elements N.
- The function h must be quickly calculated. In our today's analysis, we will consider the time for calculating h (x) as a constant. However, it is worth remembering that it should not be too complex, because it affects the overall execution time.
Given this, the search time for the element x is O (the list size is A [h (x)]). The same is true for deletions. Inserts take O (1) time, regardless of the length of the lists. So we want to analyze how big these lists are.
Basic intuition: one of the ways to distribute elements beautifully is to distribute them randomly. Unfortunately, we cannot simply use a random number generator to decide where to send the next element, because then we can never find it again. So, we want h to be something “pseudo-random” in some formal sense.
We will now set out some bad news, and then some good news.
Statement 1 (Bad News) For any hash function h, if | U | ≥ (N −1) M +1, there is a set S of N elements that are all hashed in one place.
Proof: according to the Dirichlet principle. In particular, to consider the contraposition, if each location had at most N - 1 U elements hashing it, then U could have a size of at most M (N - 1).
This is partly why hashing seems so mysterious - how can you say that hashing is good, if for any hash function you can think of ways to prevent it? One answer is that there are a lot of simple hash functions that work well in practice for typical sets S. But what if we want to get a good guarantee of the worst case?
Here's the key idea: let's use randomization in our design h, by analogy with the randomized quick sort. (Needless to say, h is a deterministic function). We show that for any sequence of insertion and search operations (we do not need to assume that the set of inserted elements of S is random), if we choose h in this probabilistic way, the performance of h in this sequence will be good in waiting. Thus, this is the same guarantee as in randomized quicksort or traps. In particular, this is the idea of universal hashing.
As soon as we develop this idea, we will use it for a particularly nice application called “perfect hashing”.
4. Universal hashing
Definition 1. Randomized algorithm H for constructing hash functions h: U → {1, ..., M}
is universal if for all x! = y in U we have
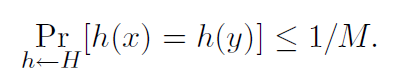
We can also say that the set H of hash functions is a universal family of hash functions, if the procedure “choose h ∈ H at random” is universal. (Here we identify a set of functions with a uniform distribution over the set.)
Theorem 2. If H is universal, then for any set S ⊆ U of size N, for any x ∈ U (for example, which we could look for), if we build h randomly according to H, the expected number of collisions between x and others elements in S no more than N / M.
Proof: every y ∈ S (y! = X) has no more than 1 / M chance of colliding with x by the definition of “universal”. So,
- Let Cxy = 1 if x and y collide, and 0 otherwise.
- Let Cx denote the total number of collisions for x. So, Cx = Py∈S, y! = X Cxy.
- We know that E [Cxy] = Pr (x and y collide) ≤ 1 / M.
- Thus, by linearity, the expectation is E [Cx] = Py E [Cxy] <N / M.
Now we get the following corollary.
Corollary 3. If H is universal, then for any sequence of operations L insert, search and delete, in which there can be no more than M elements in the system at the same time, the expected total cost of L operations for random h ∈ H is equal to O (L) (viewing time to calculate h as a constant).
Proof: for any given operation in sequence, its expected cost is constant by Theorem 2, therefore the expected total cost of L operations is O (L) in linearity of expectation.
The question is: can we actually build a universal H? If not, then this is all pretty pointless. Fortunately, the answer is yes.
4.1. Creating a universal hash family: matrix method
Suppose the keys are u-bit in length. Say, the size of the table M is equal to degree 2, so the index is the length of b-bits with M = 2b.
What we will do is choose h as the random matrix 0/1 b-by-u and define h (x) = hx, where we add mod 2. These matrices are short and thick. For example:

Statement 4. For x! = Y, Prh [h (x) = h (y)] = 1 / M = 1 / 2b.
Proof: First, what does multiplying h by x mean? We can think of this as adding some of the columns of h (doing vector addition mod 2), where 1 bit in x indicates which ones to add. (for example, we added the 1st and 3rd columns h above)
Now take an arbitrary pair of keys x, y such that x! = Y. They should differ somewhere, so, let's say, they differ in the i-th coordinate, and for concreteness, say xi = 0 and yi = 1. Imagine that first we chose all h except the i-th column. For the remaining samples of the ith column, h (x) is fixed. However, each of the 2b different settings of the i-th column gives a different value of h (y) (in particular, each time we turn a bit in this column, we turn the corresponding bit in h (y)). Thus, there is exactly a 1 / 2b chance that h (x) = h (y).
There are other methods for constructing universal hash families, also based on multiplying prime numbers (see Section 6.1).
The next question we will consider is: if we correct the set S, can we find the hash function h such that all searches will have constant time? The answer is yes, and this leads to the topic of perfect hashing.
5. Perfect hashing
We say that the hash function is ideal for S if all searches occur in O (1). Here are two ways to build perfect hash functions for a given set of S.
5.1 Method 1: Solution in O (N2) space
Let's say we want to have a table whose size is quadratic in size N of our dictionary S. Then here is a simple method for constructing an ideal hash function. Let H be universal and M = N2. Then just choose a random h from H and try it! The assertion is that there is at least a 50% chance that she will not have collisions.
Proposition 5. If H is universal and M = N2, then Prh∼H (no collisions in S) ≥ 1/2.
Evidence:
• How many pairs (x, y) are there in S? Answer:

• For each pair, the probability of their collision is ≤ 1 / M by definition universality.
• So, Pr (there is a collision) ≤
 / M <1/2.
/ M <1/2.It’s like the other side of the “birthday paradox”. If the number of days is much more than the number of people in the square, then there is a reasonable chance that no couple will have the same birthday.
So, we just choose a random h from H, and if there are any collisions, we simply choose a new h. On average, we only need to do this twice. Now, what if we want to use only the O (N) space?
5.2 Method 2: Solution in O (N) space
The question of whether you can achieve perfect hashing in O (N) space has been open for some time: “Should the tables be sorted?”. That is, for a fixed set, you can get a constant search time only with linear space? There was a series of more and more complex attempts, until finally it was solved using the good idea of universal hash functions in a two-level scheme.
The method consists in the following. First we will hash into a table of size N using universal hashing. This will lead to some collisions (unless we are lucky). However, then we rehash each basket using method 1, squaring the size of the basket to get zero collisions. Thus, the scheme is that we have the first level hash function h and the first level table A, and then the second level N hash functions h1, ..., hN and N of the second level table A1, ..., A.N ... To find the element x, we first calculate i = h (x), and then find the element in Ai [hi (x)]. (If you did this in practice, you could set the flag so that you take the second step only if there were actually collisions with the index i, and otherwise you would just put x in A [i], but let's let's not worry about it here.)
Say, the hash function h hashes n elements S to location i. We have already proved (by analyzing method 1) that we can find h1, ..., hN, so that the total space used in the secondary tables is Pi (ni) 2. It remains to show that we can find a first-level function h such that Pi (ni) 2 = O (N). In fact, we show the following:
Theorem 6. If we choose the starting point h from the universal set H, then
Pr[X i (ni)2 > 4N] < 1/2. Evidence. We prove this by showing that E [Pi (ni) 2] <2N. This implies what we want from Markov's inequality. (If there was even a probability of 1/2 that the amount could be more than 4N, then this fact in itself would mean that the expectation should have been more than 2N. Thus, if the expectation is less than 2N, the probability of failure should be less 1/2.)
Now, the tricky trick is that one of the ways to calculate this number is to count the number of ordered pairs that have collisions, including collisions with themselves. For example, if the basket has {d, e, f}, then d will have a collision with each of {d, e, f}, e will have a collision with each of {d, e, f}, and f will have a conflict with each of {d, e, f}, so we get 9. So, we have:
E[X i (ni)2] = E[X x X y Cxy] (Cxy = 1 if x and y collide, else Cxy = 0) = N +X x X y6=x E[Cxy] ≤ N + N(N − 1)/M (where the 1/M comes from the definition of universal) < 2N. (since M = N) So, we simply try a random h from H until we find such that Pi n2 i <4N, and then, fixing this function h, we find N secondary hash functions h1, ..., hN as in method 1.
6. Further discussion
6.1 Another universal hashing method
Here is another method for constructing universal hash functions, which is slightly more efficient than the matrix method given earlier.
In the matrix method, we considered the key as a vector of bits. In this method, instead, we will consider the key x as a vector of integers [x1, x2, ..., xk] with the only requirement that each xi be in the range {0, 1, ..., M-1}. For example, if we hash strings of length k, then xi may be the i-th character (if the size of our table is at least 256) or the i-th pair of characters (if the size of our table is at least 65536). In addition, we will require that the size of our table M is a prime number. To choose the hash function h, we will select k random numbers r1, r2, ..., pk from {0, 1, ..., M - 1} and determine:
h(x) = r1x1 + r2x2 + . . . + rkxk mod M. The proof that this method is universal is constructed in the same way as the proof of the matrix method. Let x and y be two different keys. We want to show that Prh (h (x) = h (y)) ≤ 1 / M. Since x! = Y, there must be a case when there exists some index i such that xi! = Yi. Now imagine that you first selected all random numbers rj for j! = I. Let h ′ (x) = Pj6 = i rjxj. So, choosing ri, we get h (x) = h ′ (x) + rixi. This means that we have a collision between x and y precisely when
h′(x) + rixi = h′(y) + riyi mod M, or equivalently when ri(xi − yi) = h′(y) − h′(x) mod M. Since M is simple, division by a non-zero value mod M is valid (every integer from 1 to M −1 has a multiplicative inverse modulo M), which means that there is exactly one value ri modulo M for which the above equation true, namely ri = (h (y) - h (x)) / (xi - yi) mod M. Thus, the probability of this occurrence is exactly 1 / M.
6.2 Other uses of hashing
Suppose we have a long sequence of elements, and we want to see how many different elements are in the list. Is there a good way to do this?
One way is to create a hash table, and then make one pass through the sequence, making a search for each element and then inserting it if it is not already in the table. The number of individual elements is simply the number of inserts.
And now that if the list is really huge and we do not have a place to store it, but an approximate answer will suit us. For example, imagine that we are a router and observe how many packets pass, and we want (approximately) to see how many different source IP addresses exist.
Here's a good idea: let's say we have a hash function h, which behaves like a random function, and let's imagine that h (x) is a real number from 0 to 1. One thing we can do is just keep track of the minimum The hash cost has been generated so far (so we won't have a table at all). For example, if the keys are 3, 10, 3, 3, 12, 10, 12 and h (3) = 0.4, h (10) = 0.2, h (12) = 0.7, then we get 0, 2
The fact is that if we choose N random numbers in [0, 1], the expected minimum value will be 1 / (N + 1). In addition, there is a good chance that it is pretty close (we can improve our estimate by running several hash functions and taking the median of the minima).
Question: why use a hash function, and not just choose a random number every time? This is because we care about the number of different elements, not just the total number of elements (the problem is much simpler: just use the counter ...).
Friends, was this article helpful to you? Write in the comments and join the open day , which will be held on April 25th.
Source: https://habr.com/ru/post/448992/
All Articles