How to spread all on science and not to turn the office into a hotbed of hatred

Sooner or later in the life of most of the teams, it comes - the move. You are led to a clean empty room, which will become the place where you will spend most of your life. If you are a designer, then first of all you will figure out how to hang out pictures and put flowers to make the room play with new colors. If you are an experienced office samurai, then immediately with a trained eye determine the best place and claim it first. If you are the head of a department, then a headache for the seating of all the staff will surely visit you. But if at the same time you are leading a team of datascentists, then a Python coin will help you.

Of course, everything is determined by your management style. If you prefer authoritarian decisions, you can simply tell with an imperious finger where to go. And it does not matter if someone resists sitting face down on a wall or towards each other. However, since the abolition of serfdom in 1861, this style in our country gradually loses its popularity. And if you are still concerned about the comfort of employees, then it is worthwhile to collect and somehow take into account their preferences. But it is here that the devil sneaks up, the very one that is in the details: how to assemble, how to take into account, to whom to give preference, etc.

Due to the many years of experience in organizing competitions for schoolchildren, where equality of conditions is one of the main priorities, I was determined to create transparent and understandable mechanisms under which more experienced or fast employees do not receive any advantages.
')

You will not please everyone or all the same ...?

We are making the premise that employees may have preferences for seating, and want to minimize possible dissatisfaction. That is, it is necessary to organize a system for allocating places so that some employees, acting in an optimal way for themselves, do not enter into obvious conflict with others. The strategy of "who first got up, that and sneakers" clearly does not lead to this goal. If, however, to determine some sort of order of choice (for example, on the basis of merit), then the task is still not solved - a person who chooses earlier, but who is relatively all the same, may accidentally take a place chosen by others. Not to mention the fact that such an order is a disputed thing in itself.

We chose the type of voting, in which each vote depends on how the others voted: if a person is more or less interested in which of the two places to sit down, then the optimal strategy is to claim where there are fewer competitors.

Our way to perfect seating

First of all, it was necessary to determine where to sit at all. Here the task was for everyone, because everyone is interested in making as many convenient places as possible - in this case, competition decreases. We made a map and carried out explanatory work "among the population", promoting each place as perfect.



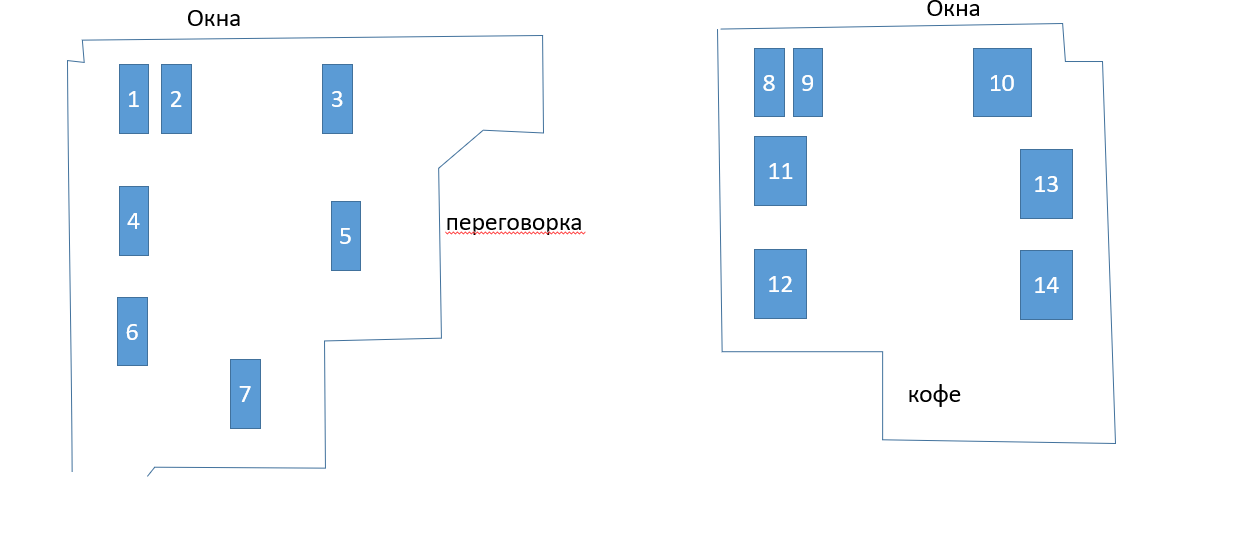
In an ideal world, it would be necessary for each to set points of preference for each of the places, but it is difficult for a person to estimate, to the hundredths, how one place differs from another.
Therefore, each was asked to choose lists of priorities, the number of which is generally unlimited: which places he would like to take in the first place, which - in the second, and which - in the third.

It should be noted here that the logic of employee preferences was very different: someone wanted to be closer to the window, someone to look out the window, someone wanted proximity to the air conditioner and even the color of the walls. The preferences themselves are difficult to take into account, here you can only give people the opportunity to choose a place.

Next was required to determine the metrics of the success of the arrangement. The more inconvenient a person sits, the more such a model should be fined. I decided to make a quadratic penalty to avoid blatant inconveniences.

It turned out this way: if a person was put on a place from his TOP-1 list, then a fine is 2; if from the list of TOP-2 - fine 4, TOP-3 - 8, TOP-4 - 16 and so on. I do not claim that this metric is optimal, but it looks reasonable.

I wrote a simple program in Python - priorities from colleagues are entered into it, and it calculates placement options with a minimum penalty. The algorithm was announced to colleagues in advance (as I was naive!). Lists all published in the open, to be able, if desired, to agree.

However, after seeing the calculations, some employees realized that they could try to pick up their “application” in order to get the required place. Datasayantists are datastheists! :)

As a result, the second round of elections was organized, when it was possible to make changes in their priorities in the closed one. Thus, everyone was again on an equal footing - everyone could select and make changes.

Having collected applications from the second round, I drove the program already final. Fufh! It seems everyone is happy.

Instead of PS

It is worth noting that there were not taken into account the wishes about the proximity of employees to each other. But in this paradigm they are also quite simple to implement by creating wish lists (who wants to sit with whom and which places are close, according to these employees), and then penalize the model for not fulfilling these wishes.

Of course, there is always an option when two layouts have the same penalty.
In this case, I have already decided to rely on the coin - optimization is powerless further :).

Nikolai Knyazev, the head of the Jet Infosystems machine learning group

GitHub Code