Create procedural planets globes
Distortion, seamless noise and how to work with them.

One of the easiest ways to generate a planet is to use noise. If we decide to choose it, then we have a couple of options. Let's look at each and determine the best:
Of these three, I personally prefer Open Simplex Noise, which I use in my personal projects. It is worth noting that in the current implementation of OpenSimplexNoise, getting simple access to scale, octaves, and generator values will require additional work. There is a wealth of information on the Internet about what each of these elements does, and I highly recommend that you study it. However, in my article I will not talk about it.

This is what Open Simplex Noise looks like with 16 octaves.
')
The noise is infinite, which means that if we simply create a canvas with a 2: 1 aspect ratio, to get an equidistant projection , then it will not be looped over to the sphere (I am grateful to this amazing website), and on the horizontal seam and at the poles huge differences.
Noise created without seams.
Notice the huge seams that appeared when imposing noise on the sphere.
You can fix this in many ways; for example, in this excellent post Red Blob Games [ transfer to Habré] it was enough just to generate an island using a function that takes as a variable the distance to the center and and sets the heights to 0 to minimize the seams.
However, we do not need this. We want to generate a planet with the possibility of the existence of the north and south poles, and for this we will need more complex mathematical calculations.
The method capable of generating spherical planets is to convert the Cartesian coordinates of our canvas into spherical coordinates, generate noise based on these coordinates, and then convert the noise back to Cartesian coordinates and impose it on the canvas.
However, this implementation has its limitations, the causes of which are shown in a stunning post by Ron Valstar . The most important thing is that the forms of the continents in this case look extremely strange and distorted, and therefore we will not use this option.
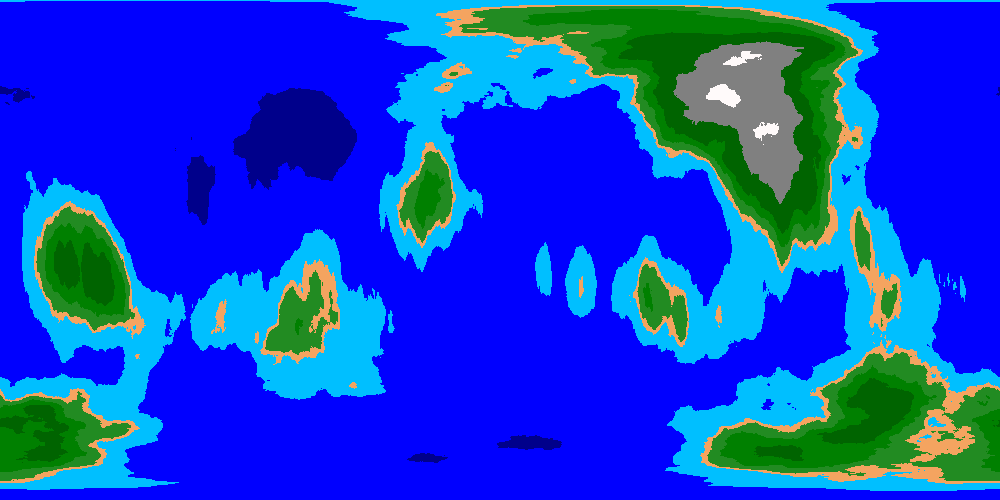
Spherical noise overlay. Strange shapes and distortions make the continents rather ugly.
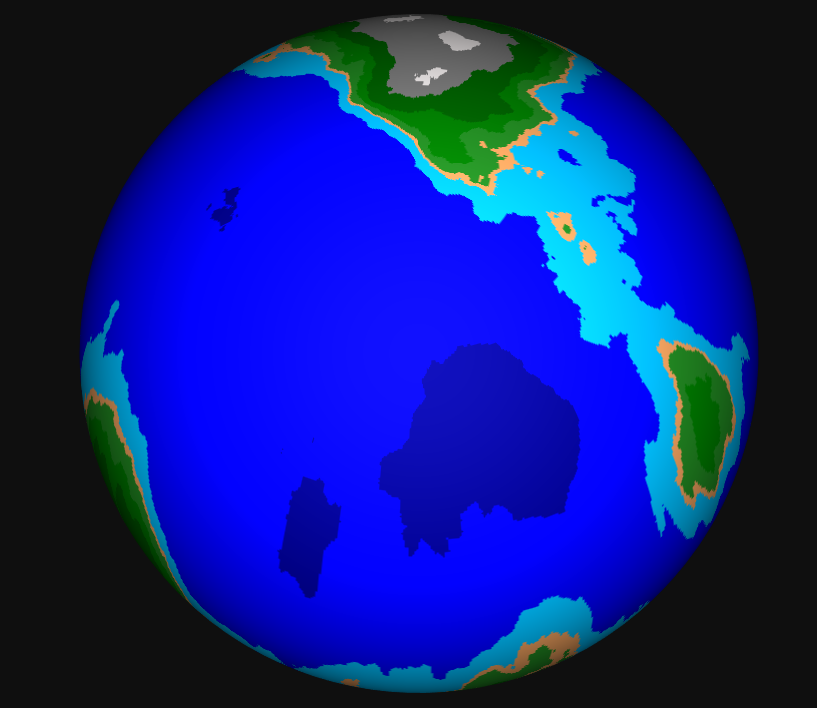
But at least there are no more stitches.
As a result, I used the second method, taken from the post of Ron Walstar and a series of articles acko Making Worlds . They describe the generation of a globe through the generation of a cube and its “inflation”, as if it were a balloon, as long as it does not exemplify the shape of a sphere.
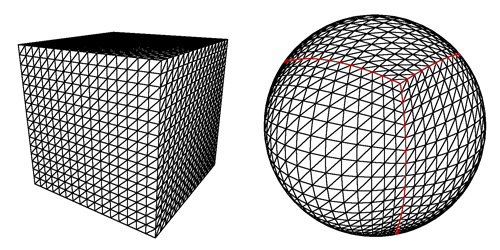
Image taken from acko.net. It explains the concept of a cubic map in an easy-to-visual form.
Now we just need to generate six faces, which is quite simple, there are many ways to do this.
In the end I decided to create an array and fill it with data. I converted the 2D coordinates of the canvas to the 3D coordinates of the cube, and then generated noise for each of these 3D coordinates so as to save them to the corresponding value of the 2D coordinates.
In this way, we can create a cubic map that is easily converted to an equidistant projection using the wonderful code written by Bartosz .

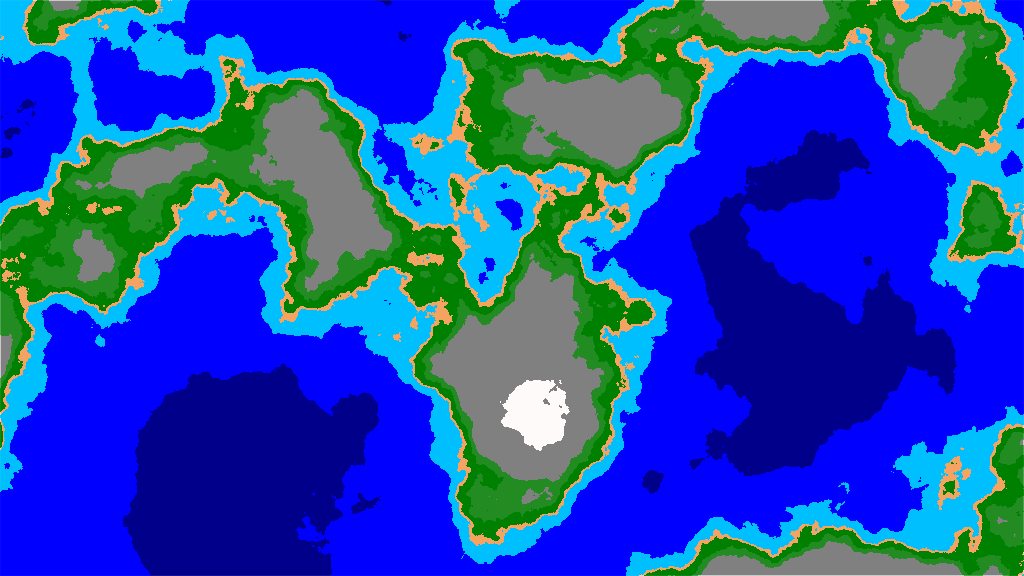
Algorithm generated cubic map.

Equivalent conversion of a cubic map.

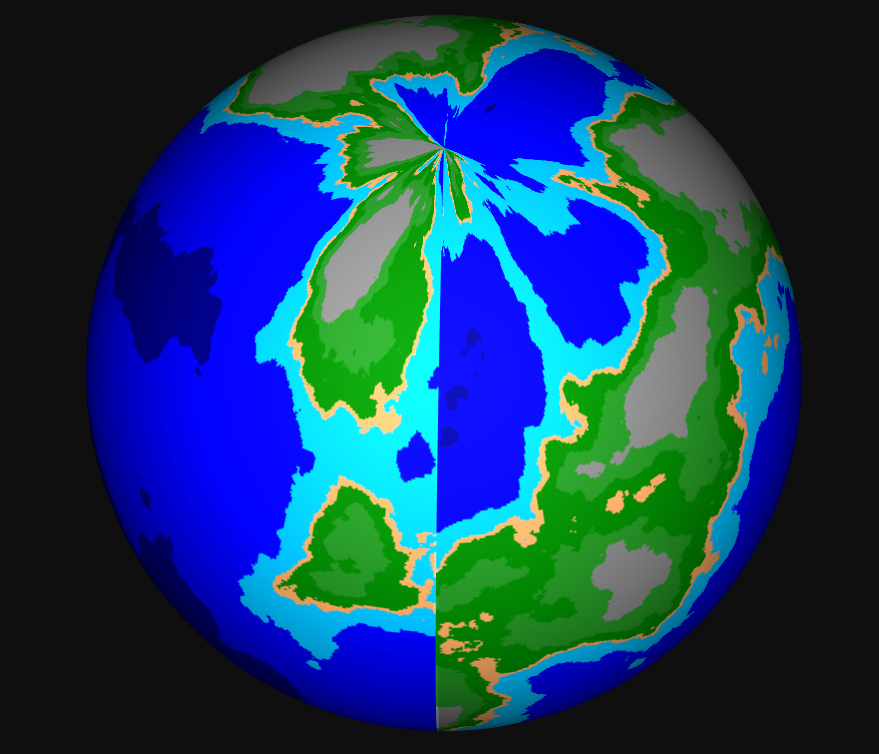
Globe cubic map, rendered on the site maptoglobe.com .
As you can see, the equidistant map has much more beautiful forms, and when applied to a sphere, it creates results similar to spherical imposition, without having all its flaws. By the way, the equidistant projection can be easily converted by different programs, for example, NASA G.Projector , into almost any type of map.
Generating an entire planet may seem like a daunting task, and although noise, if properly used, is a fairly powerful tool, it has its own problems that people have faced for many centuries, such as putting a globe on a 2D canvas with minimal distortion.
The solution I proposed creates very roughly generated planets that do not take into account tectonic plates, rivers, chains of islands, and even mountains, and therefore it can only be used as a demonstration or as a basis for more complex simulations.
In fact, it creates only a matrix of values in a certain range of values. For grayscale images, this is a range of 0-255. The values are then converted into a pixel creating an image similar to the first image in grayscale, or into an image in the interval from -11000 to 8000 to simulate the height difference of the real world, after which the pixels are colored with colors according to the height intervals (for example, values from 0 5 are painted in the color of sand to simulate the coast) .

We generate the planet
One of the easiest ways to generate a planet is to use noise. If we decide to choose it, then we have a couple of options. Let's look at each and determine the best:
- Perlin Noise is the easiest option. Perlin's noise was developed by Ken Perlin in 1983, it has a couple of drawbacks - visual artifacts and a rather low speed when generating large images.
- Simplex Noise - developed by Ken Perlin in 2001 as an attempt to eliminate the shortcomings of Perlin noise; This is a worthy and quick solution, but with a serious drawback: the use of three-dimensional simplex noise is protected by a patent, which makes it quite expensive.
- Open Simplex Noise - KDotJPG was developed with one simple goal: to create a modern and free version of simplex noise, relatively fast and without distortion.
Of these three, I personally prefer Open Simplex Noise, which I use in my personal projects. It is worth noting that in the current implementation of OpenSimplexNoise, getting simple access to scale, octaves, and generator values will require additional work. There is a wealth of information on the Internet about what each of these elements does, and I highly recommend that you study it. However, in my article I will not talk about it.

This is what Open Simplex Noise looks like with 16 octaves.
')
Seamless noise
The noise is infinite, which means that if we simply create a canvas with a 2: 1 aspect ratio, to get an equidistant projection , then it will not be looped over to the sphere (I am grateful to this amazing website), and on the horizontal seam and at the poles huge differences.

Noise created without seams.

Notice the huge seams that appeared when imposing noise on the sphere.
You can fix this in many ways; for example, in this excellent post Red Blob Games [ transfer to Habré] it was enough just to generate an island using a function that takes as a variable the distance to the center and and sets the heights to 0 to minimize the seams.
However, we do not need this. We want to generate a planet with the possibility of the existence of the north and south poles, and for this we will need more complex mathematical calculations.
Spherical overlay
The method capable of generating spherical planets is to convert the Cartesian coordinates of our canvas into spherical coordinates, generate noise based on these coordinates, and then convert the noise back to Cartesian coordinates and impose it on the canvas.
However, this implementation has its limitations, the causes of which are shown in a stunning post by Ron Valstar . The most important thing is that the forms of the continents in this case look extremely strange and distorted, and therefore we will not use this option.

Spherical noise overlay. Strange shapes and distortions make the continents rather ugly.

But at least there are no more stitches.
Cubic overlay
As a result, I used the second method, taken from the post of Ron Walstar and a series of articles acko Making Worlds . They describe the generation of a globe through the generation of a cube and its “inflation”, as if it were a balloon, as long as it does not exemplify the shape of a sphere.

Image taken from acko.net. It explains the concept of a cubic map in an easy-to-visual form.
Now we just need to generate six faces, which is quite simple, there are many ways to do this.
In the end I decided to create an array and fill it with data. I converted the 2D coordinates of the canvas to the 3D coordinates of the cube, and then generated noise for each of these 3D coordinates so as to save them to the corresponding value of the 2D coordinates.
//Z STATIC for(int y = 0; y < cubeFaceSize; y++) { for(int x = 0; x < cubeFaceSize * 2; x++) { //Generates FRONT if(x < cubeFaceSize) { cubeMap[cubeFaceSize+x][cubeFaceSize+y] = noise.noise3D(x, y, 0); } //Generates BACK else { cubeMap[cubeFaceSize*3+(x-cubeFaceSize)][cubeFaceSize+y] = noise.noise3D(cubeFaceSize-(x-cubeFaceSize), y, cubeFaceSize); } } } //X STATIC for(int y = 0; y < cubeFaceSize; y++) { for(int x = 0; x < cubeFaceSize * 2; x++) { //Generates LEFT if(x < cubeFaceSize) { cubeMap[x][cubeFaceSize+y] = noise.noise3D(0, y, cubeFaceSize-x); } //Generates RIGHT else { cubeMap[cubeFaceSize*2+(x-cubeFaceSize)][cubeFaceSize+y] = noise.noise3D(cubeFaceSize, y, x-cubeFaceSize); } } } //Y STATIC for(int y = 0; y < cubeFaceSize * 2; y++) { for(int x = 0; x < cubeFaceSize; x++) { //Generates TOP if(y < cubeFaceSize) { cubeMap[cubeFaceSize+x][y] = noise.noise3D(x, 0, cubeFaceSize-y); } //Generates BOTTOM else { cubeMap[cubeFaceSize+x][cubeFaceSize*2+(y-cubeFaceSize)] = noise.noise3D(x, cubeFaceSize, y-cubeFaceSize); } } } In this way, we can create a cubic map that is easily converted to an equidistant projection using the wonderful code written by Bartosz .

Algorithm generated cubic map.

Equivalent conversion of a cubic map.

Globe cubic map, rendered on the site maptoglobe.com .
As you can see, the equidistant map has much more beautiful forms, and when applied to a sphere, it creates results similar to spherical imposition, without having all its flaws. By the way, the equidistant projection can be easily converted by different programs, for example, NASA G.Projector , into almost any type of map.
Finally
Generating an entire planet may seem like a daunting task, and although noise, if properly used, is a fairly powerful tool, it has its own problems that people have faced for many centuries, such as putting a globe on a 2D canvas with minimal distortion.
The solution I proposed creates very roughly generated planets that do not take into account tectonic plates, rivers, chains of islands, and even mountains, and therefore it can only be used as a demonstration or as a basis for more complex simulations.
In fact, it creates only a matrix of values in a certain range of values. For grayscale images, this is a range of 0-255. The values are then converted into a pixel creating an image similar to the first image in grayscale, or into an image in the interval from -11000 to 8000 to simulate the height difference of the real world, after which the pixels are colored with colors according to the height intervals (for example, values from 0 5 are painted in the color of sand to simulate the coast) .
In constructing the universe, God used the highest level of mathematics.
- Paul Dirac
Source: https://habr.com/ru/post/448324/
All Articles