Where evidence, facts and imagination converge

In mathematics, where proof is everything, facts are also important. However, the facts are good, only while the model is good, and building models is unreliable. So how many facts will suffice?

Can you find the next number in the sequence?



1, 2, 4, 8

')

Here is another number for you if you need more data to make a decision:



1, 2, 4, 8, 16



The next number should be 32, right? The pattern is clear: to find the next number, you need to double the previous one. 1 × 2 = 2; 2 × 2 = 4; 4 × 2 = 8; 8 × 2 = 16. So the next number should be 16 × 2 = 32. How many more facts are needed to confirm this?



But, although it is quite reasonable to assume that the next number will be 32, this will not always be true. Consider the following sequence: we will calculate the number of sections into which the circle is broken, connecting the points located on the circle.







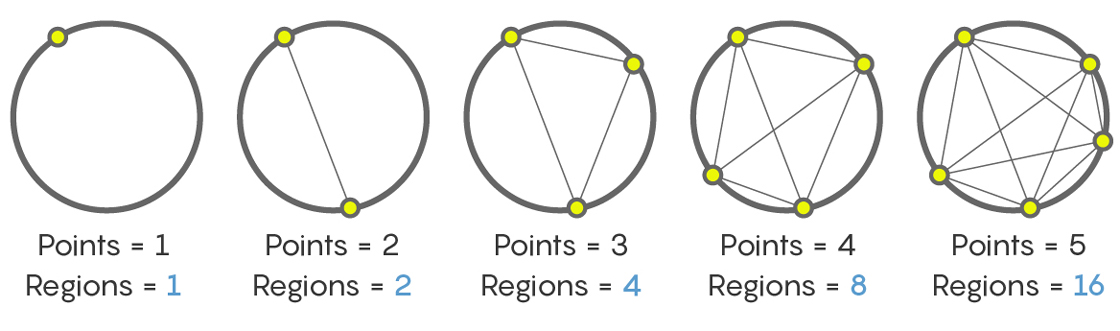
One point gives one segment (the entire inner part of the circle). Two points - two plots. Three points - four plots. Five and six are eight and sixteen, respectively. The result is a sequence



1, 2, 4, 8, 16



And how many sections will appear after connecting lines of six points on a circle? No one will condemn you, if you, like many people who are facing this task for the first time, say that 32. But this is not so. In fact, no matter how annoying, the answer will be - 31! Count yourself, and then check again.







Of course, there are sequences of types 1, 2, 4, 8, 16, 32, 64, and so on, from double numbers each time. But there are other sequences, for example, the maximum number of sections into which the circle is broken, the lines connecting the points on the circle, and this is already 1, 2, 4, 8, 16, 31, 57, 99, and so on. Meeting the sequence of 1, 2, 4, 8, 16, we can think that all the facts are for the fact that the next number will be 32, but there may be something else.



Mathematics has a long tradition of challenging our expectations and making our imagination work. Therefore, mathematicians always strive to obtain rigorous proof, not just facts. The proof establishes a mathematical truth. All facts may indicate 32 as the next number in our sequence, but without strict proof we cannot be sure of it.



Still, the facts for mathematicians are useful and important. Often, before proving anything, we play with the available information, study the problem, consider examples and collect data. We study and weigh the facts and decide what to do next. These results form our opinion, proposing to prove some theorems and refute others.



The twin conjecture hypothesis is one example where facts govern our mathematical thinking in the same way as evidence. Twin prime numbers are pairs of prime numbers that differ by 2 — for example, 3 and 5, 11 and 13, 101 and 103. The hypothesis about twin numbers suggests that there is no largest pair of such twins — that is, similar pairs constantly appear on the number line when moving to infinity.



The twin conjecture is not a theorem, since, despite the fact that this is one of the most famous problems in number theory, no one has yet been able to prove it. However, almost everyone believes that it is true, because there are many facts in its support.



For example, in our search for prime numbers, we constantly find extremely large pairs of prime twin numbers. Each of the prime numbers of the largest known pair contains 400,000 digits each. Theorems similar to this hypothesis are also proved. In 2013, Zhang Ethan shocked the mathematical community by proving the existence of an infinitely large number of pairs of prime numbers, differing by no more than 70 million. Thanks to the open source project Polymath, we know that there are an infinite number of pairs of prime numbers that differ from each other by no more than 246 . We still have not proved the existence of an infinite number of pairs of prime numbers differing by 2 - but still 2 is much closer to 246 than 246 to infinity.



For these and other reasons, the belief in justice, even if it is not a proven hypothesis, is not very controversial. However, there are other areas of mathematics in which facts are used to build an informed opinion that turns out to be more controversial.



In the study of elliptic curves, its rank, roughly speaking, denotes a numerical estimate of the complexity of solving this curve. For many years it was believed that the ranks of elliptic curves are not limited , that is, there are no restrictions on the value of the rank of the curve, or on the complexity of the solution.



However, recent work makes mathematicians think about the possibility of limited rank. The paper gives facts that indicate that there may be a finite number of curves whose rank is greater than 21.



However, caution should be exercised. The facts collected by mathematicians are not taken from the world of elliptic curves — they refer to matrices that the researchers used to model the curves. Mathematical models are universally used in science, and they can even be turned inward to study mathematics itself. These are incredibly powerful tools that allow us to replace an incomprehensible task with one that is easier for us to handle.



But using models is a tricky business. One can never be sure that the model behaves quite similar to what we are trying to understand so that we can draw conclusions from its behavior. It is also impossible to be sure that our model is similar exactly in the places of greatest importance. Therefore, it is difficult to make sure that the facts collected by us on the basis of models really indicate the real properties of the phenomena we are studying. Let's explore these problems based on a simple model of a simple hypothesis.



Imagine that we want to study the following statement: any two lines either intersect or are parallel.



By intersection, we mean that straight lines have a common point, and parallelism is the fact that they go in one direction, but do not intersect (this concept can be defined in a different way, but I will use it for simplicity).



To investigate this issue, create a model. Each straight line is represented by the oblique straight equation, which you can remember from the school course. That is, we assume that each straight line can be described by an equation of the form



y = mx + b



where m is the slope of the line (its steepness), and b is the point of intersection of the y-axis (vertical axis).



Simulation of lines in this way is convenient for experiments on them. The model allows us to create a random line by selecting a pair of random numbers, m and b. We can choose a pair of random lines and check them - do they intersect? Do they go one way? Is something else happening?



Here are some examples of how the results of such experiments may look.







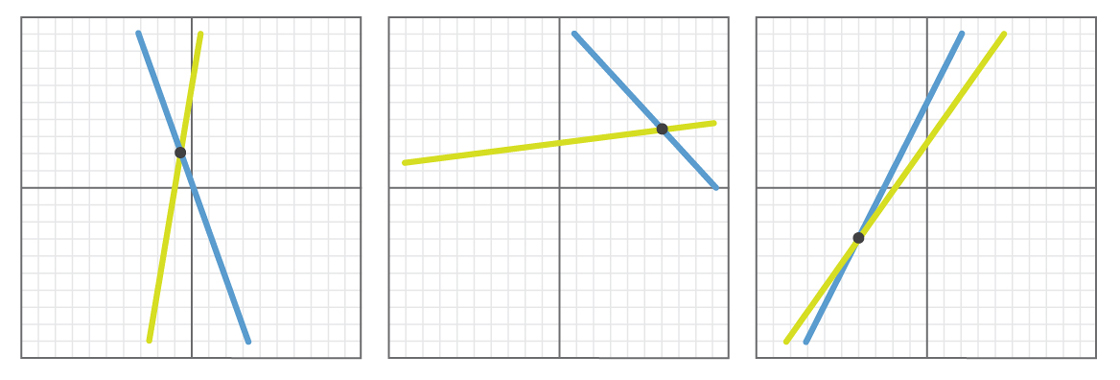
In each example, randomly selected straight lines intersect. If we conduct this experiment a thousand times — or 10,000, or a million — we find that in all cases the straight lines will intersect or will be parallel (and most likely, all the straight lines will intersect, since it is unlikely that the two straight lines will have the same slope, by chance).



Therefore, looking at a million examples, you can come to the conclusion that the hypothesis is most likely true. All the facts fully support the statement that any pair of lines is either parallel or intersects.



However, the facts are only as good as the model, and modeling is a dangerous occupation. Let's see what dangers we created for ourselves in our example.



One problem - certain types of direct will occur more often than others. Here is a graph showing 50 lines with b = 0 and 0 ≤ m ≤ 1.







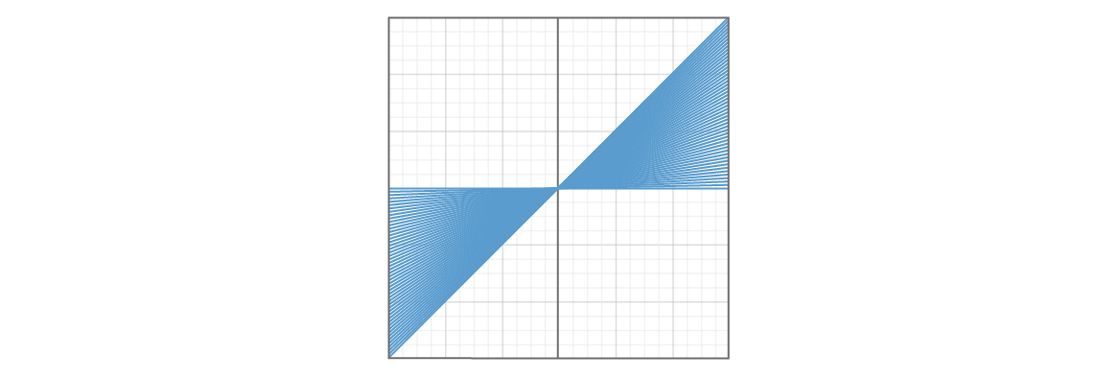
And here is a graph showing 50 lines with b = 0 and m ≥ 1.







It looks like a quarter of the plane is covered with straight lines with a slope from 0 to 1, and another quarter is straight with a slope greater than 1. Choosing a number greater than 1 seems more likely than choosing a number from 0 to 1, so the straight line is more likely will be in the second section of the plane. This means that certain straight lines, with a slope from 0 to 1, will be extremely under-represented in the model. And if in this part of the plane some strange things happen to the straight lines, our model will hardly tell us about it.



If you look closely at the second graph, we will see another problem. The more m becomes, the steeper will be straight. The steepest straight line is vertical. What is the slope of the vertical line? By definition, it is not defined: there is no such number m that could describe the vertical line. It turns out that there is no vertical straight line in our model, and we will not be able to experiment with it. We have not yet begun collecting facts, but have already excluded some special cases simply because of the model construction scheme.



The same applies to the most serious problems of our model. People who easily imagine a three-dimensional space, probably immediately noticed that our hypothesis is incorrect. Direct is not necessary or intersect, or be parallel. Imagine two corridors running in different directions on different floors of a building. These are intersecting straight lines - straight lines that do not intersect or are parallel.







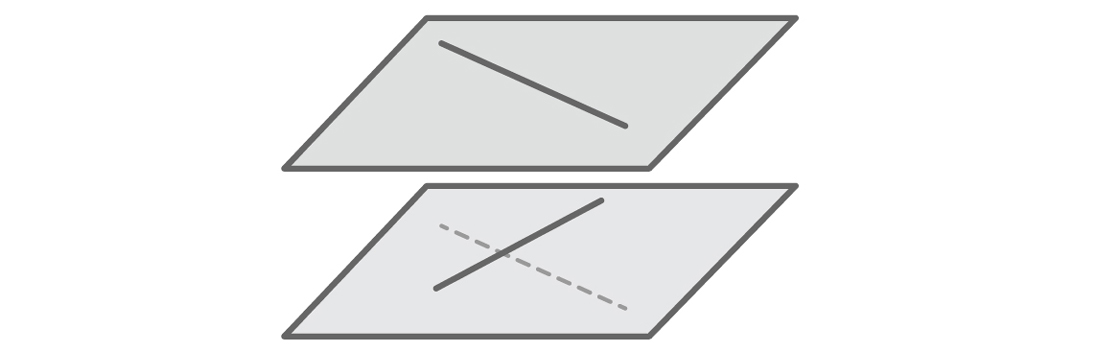
Crossing lines should lie in different planes. But since our model defines any line through the equation y = mx + b, we automatically imagine that all lines are in the same plane. Our model will produce only facts supporting our hypothesis, since if two straight lines lie in one plane, they really must either intersect or go parallel. We will not see any other facts: there are no crossed lines in our model. As in the case of vertical lines, the model eliminated what we could not imagine.



This is a simple example that uses a silly model with a bunch of problems, including tricky questions such as, for example, the procedure for choosing random numbers from infinite sets. Professional mathematicians who study the ranks of elliptic curves would never make such simplistic and obvious mistakes.



These mathematicians know what precautions to take when working with models. They know that, regardless of how useful and interesting the model will be, or how convincing the collected facts will be, properties that they have not imagined may appear in elliptic curves. And if this can not be imagined, your model will not take this into account, and, therefore, the facts will not reflect.



But the rights of the new model, or not, she made the mathematicians productively reflect on the elliptic curves. If it does reflect truth, then ideas from the world of matrices can explain the behavior of curves. If not, understanding why elliptic curves cannot be modeled in this way can lead to a better understanding of the problem. The facts collected by us may bring us closer to the evidence, one way or another.