On autoregressive estimation of the spectral density of a stationary signal
The methods of spectral estimation of stationary random processes based on the fast Fourier transform (FFT) are well known and widely used in engineering practice. Their disadvantages include, in particular, the high variance (low accuracy) of the estimate with an insufficiently long interval of observation of the process, which visually usually manifests itself in a strong “irregular” graph of the power spectral density (SPM). One of the alternative methods of spectral estimation is the autoregression method, which is considered in the example below, which is much less known in engineering practice. The method in many cases makes it relatively easy to obtain a much better estimate of the SPM (Fig. 1), and sometimes more in-depth information about the random process under investigation.

Fig.1. Classical and autoregressive estimation of the “short” process DMA
For demonstration purposes, a discrete-time signal (sequence) x [i] was synthesized. The signal is modeled using an ARMA model (digital filter) that simulates the properties of a mechanical system (1) - moving the material point x (t) in a “single-mass” oscillator with parameters m = 1 kg, c = 100 N / m, k = 2, 5 kg / s, and power perturbation — Gaussian “white” (taking into account discretization) noise f (t) with dispersion 1 H 2 , time interval discretization Δt = 0.12 s.
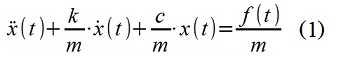
')
Built model (2). The model building method has already been considered here .
x [i] - 0.6388 · x [i-1] + 0.7408 · x [i-2] = 0.009667 · f [i-1] (2)
Using (2), a sequence of 50 thousand samples was synthesized, for which the generator of the normally distributed random variable randn () of the well-known software environment was used.
After the process of modeling x [i] is completed, the quantitative parameters of model (2) are assumed to be unknown — only the process itself is available for research and, to some extent, information on the properties of the model in its most general terms.
A spectral estimation of a 50,000-point sequence by the Welch method was carried out, the segment size was assumed to be 256 samples, a Hamming window and 60% segment overlap were applied. The standard deviation of this estimate, assuming that the sequence has a length of about 200 non-overlapping segments, can be roughly estimated as ~ 7%.
Further, assuming that a far less lengthy sequence is available in the experiment in real conditions in the experiment, studies were conducted only from the first 500 samples of this signal.
The estimation was obtained by the Welch method with the same parameters. RMS of such an estimate of ~ 70%, a very strong “irregular” graph is noticeable (Fig. 2).

Fig.2. Evaluation of the "long" and "short" PMT by the classical method
Based on the fact that the approximate form of the function (graphics) of the SPM process is known to us (for example, based on the known physical nature of the process — a single-mass oscillator under white noise, or from evaluating similar processes for which longer implementations are available), it was decided to evaluate using a second-order autoregression model (AR (2), or = ARMA (2.0)).
Determining the order of the model is a very important point; an error in the order may entail very gross errors in the results of the evaluation. There are methods that are not considered here, which help in determining the order of the model based on only the process being analyzed.
Estimation of the model parameters is produced using the well-known Yul-Walker equations for the autoregressive process (slightly modified in order to simplify the script structure to some extent):
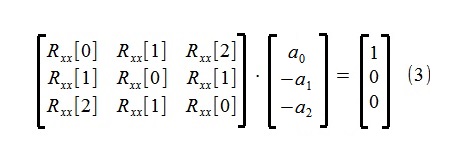
As can be seen from the equations, to determine the parameters, only the first three members of the autoregressive sequence Rxx [0], Rxx [1], Rxx [2] will be needed, which were estimated using the original 500-point sequence x [i] by the correlation method, the standard deviation ~ 4.5%.
(By the way, it is clear that the "cons" before a 1 , a2 2 , etc., are extremely inconvenient. They appeared because of the predominantly "predictive" use of ARMA models in the economy, in earlier "engineering" sources No. I already doubt that it was necessary to use such an understanding of AR-coefficients here.)
The correlation matrix in (3) in practice always has a strict diagonal dominance | Rxx [0] | > | | Rxx [i] |, including due to the presence of observation noise, as a result of which there are no difficulties with its handling (finding the solution (3)).
(To clarify the question of the magnitude of the statistical modeling error, it is interesting to mention, for example, the estimate Rxx [0] = 2.2606e-04 m 2 , obtained from 500 samples, compared to the correlating estimate of the variance from 50,000 samples, = 2.4238e-04 m 2 and an estimate for the integrating area of the SPM, obtained by the Welch method from 50,000 counts (Fig. 2), = 2.4232e-04 m 2 )
After substituting the found estimates Rxx [i], we have:

The following model parameters are defined: a 0 = 11325.9; a 1 = -7090.1; a 2 = 8411.5; As can be seen from (3), the dispersion of the hypothetical white noise here was given = 1, determining instead the gain factor a 0 . The autoregressive estimate of the SPM is constructed by Fourier transform over a sequence of coefficients a 0 , a 1 , a 2 :
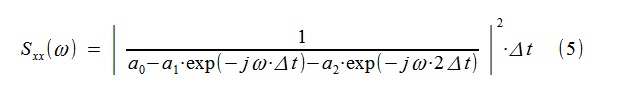
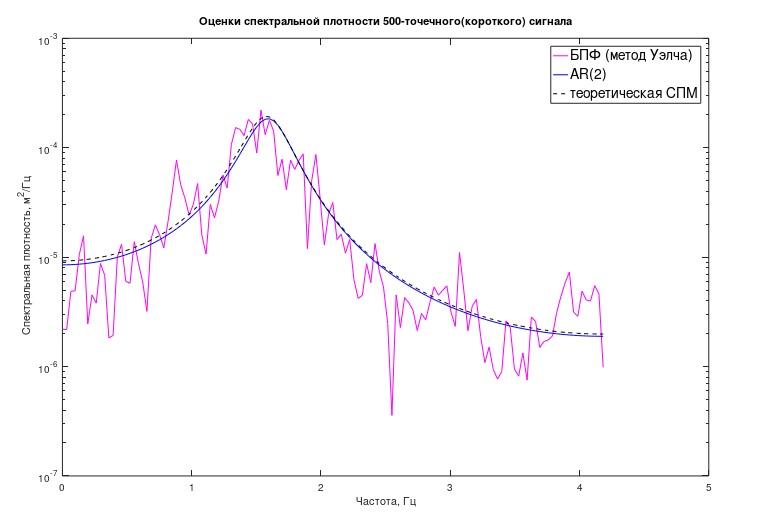
Fig.3. Classical and autoregressive estimation of the “short” process DMA
In the same way, according to an expression similar to (5), the “theoretical” SPM plot was previously constructed, only the model coefficients there, naturally, were taken different (from (2)).
From the graph it is clear that the AR-estimate of the SPM was very close to the theoretically expected. In addition to the graph, there is an opportunity to try to evaluate some of the analytical characteristics of the process and the associated mechanical system. In this case, these are the “poles” of the model, numerically characterizing the frequencies of the “resonant” peaks of the model and the associated “Q-factors”.
From (5) we find the relation for searching for discontinuities of the transfer function of our model using the Laplace transform (replacing jω with λ = -ε + jω):
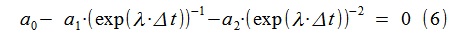
For the obtained AR-model in this way, λ 1,2 = -1.5427 ± j · 10.1514 is calculated, which is very close to the original model used to generate the process
λ 1,2 theor = -1.2500 ± j · 9.9216 (that is, the positions of the resonant peak, respectively, 1.615 Hz (in theory) and 1.579 Hz (determined)).
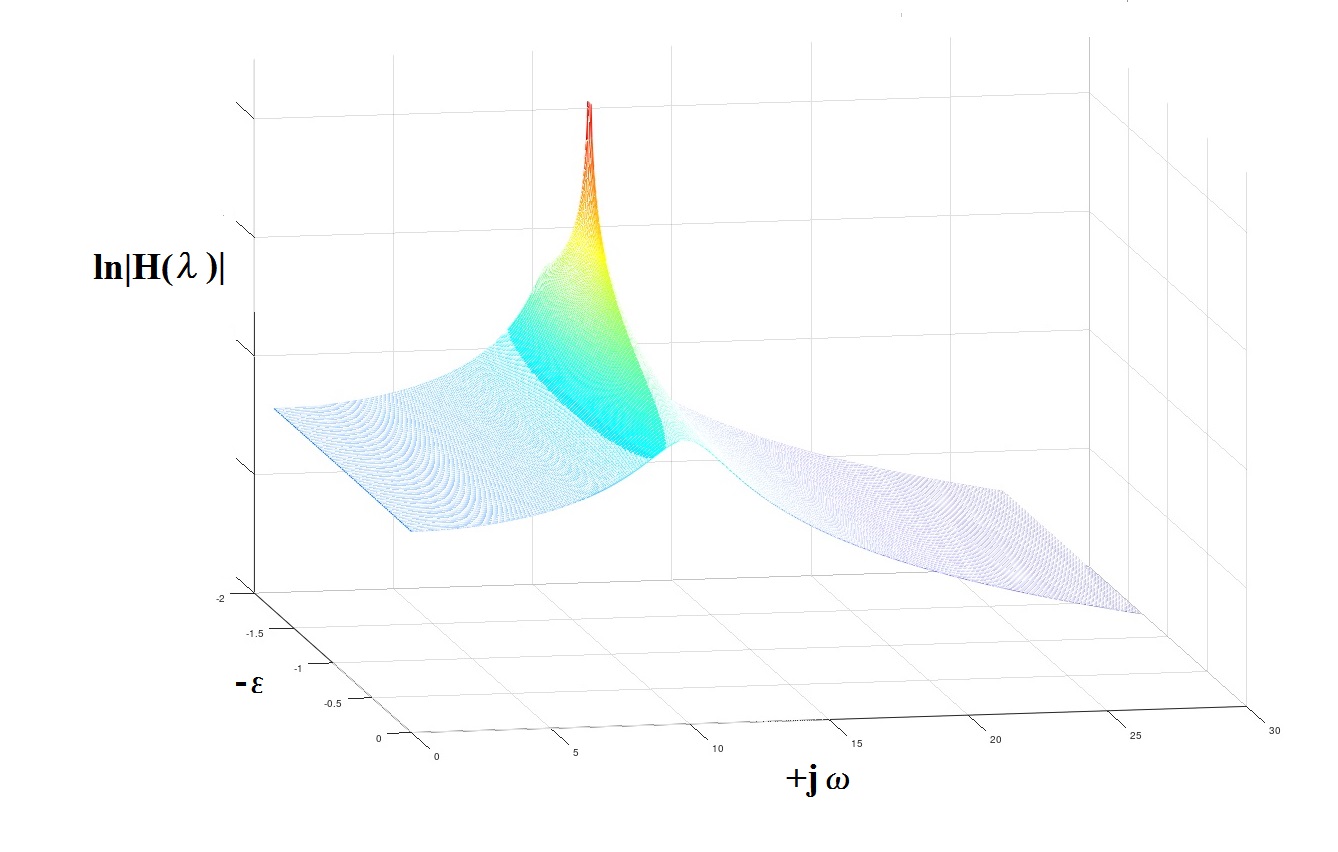
Fig.4 On the concept of "poles"
A few comments and recommendations in conclusion.

Fig.1. Classical and autoregressive estimation of the “short” process DMA
For demonstration purposes, a discrete-time signal (sequence) x [i] was synthesized. The signal is modeled using an ARMA model (digital filter) that simulates the properties of a mechanical system (1) - moving the material point x (t) in a “single-mass” oscillator with parameters m = 1 kg, c = 100 N / m, k = 2, 5 kg / s, and power perturbation — Gaussian “white” (taking into account discretization) noise f (t) with dispersion 1 H 2 , time interval discretization Δt = 0.12 s.
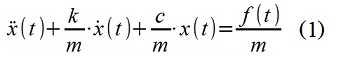
')
Built model (2). The model building method has already been considered here .
x [i] - 0.6388 · x [i-1] + 0.7408 · x [i-2] = 0.009667 · f [i-1] (2)
Using (2), a sequence of 50 thousand samples was synthesized, for which the generator of the normally distributed random variable randn () of the well-known software environment was used.
After the process of modeling x [i] is completed, the quantitative parameters of model (2) are assumed to be unknown — only the process itself is available for research and, to some extent, information on the properties of the model in its most general terms.
A spectral estimation of a 50,000-point sequence by the Welch method was carried out, the segment size was assumed to be 256 samples, a Hamming window and 60% segment overlap were applied. The standard deviation of this estimate, assuming that the sequence has a length of about 200 non-overlapping segments, can be roughly estimated as ~ 7%.
Further, assuming that a far less lengthy sequence is available in the experiment in real conditions in the experiment, studies were conducted only from the first 500 samples of this signal.
The estimation was obtained by the Welch method with the same parameters. RMS of such an estimate of ~ 70%, a very strong “irregular” graph is noticeable (Fig. 2).

Fig.2. Evaluation of the "long" and "short" PMT by the classical method
Based on the fact that the approximate form of the function (graphics) of the SPM process is known to us (for example, based on the known physical nature of the process — a single-mass oscillator under white noise, or from evaluating similar processes for which longer implementations are available), it was decided to evaluate using a second-order autoregression model (AR (2), or = ARMA (2.0)).
Determining the order of the model is a very important point; an error in the order may entail very gross errors in the results of the evaluation. There are methods that are not considered here, which help in determining the order of the model based on only the process being analyzed.
Estimation of the model parameters is produced using the well-known Yul-Walker equations for the autoregressive process (slightly modified in order to simplify the script structure to some extent):
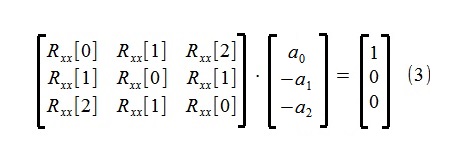
As can be seen from the equations, to determine the parameters, only the first three members of the autoregressive sequence Rxx [0], Rxx [1], Rxx [2] will be needed, which were estimated using the original 500-point sequence x [i] by the correlation method, the standard deviation ~ 4.5%.
(By the way, it is clear that the "cons" before a 1 , a2 2 , etc., are extremely inconvenient. They appeared because of the predominantly "predictive" use of ARMA models in the economy, in earlier "engineering" sources No. I already doubt that it was necessary to use such an understanding of AR-coefficients here.)
The correlation matrix in (3) in practice always has a strict diagonal dominance | Rxx [0] | > | | Rxx [i] |, including due to the presence of observation noise, as a result of which there are no difficulties with its handling (finding the solution (3)).
(To clarify the question of the magnitude of the statistical modeling error, it is interesting to mention, for example, the estimate Rxx [0] = 2.2606e-04 m 2 , obtained from 500 samples, compared to the correlating estimate of the variance from 50,000 samples, = 2.4238e-04 m 2 and an estimate for the integrating area of the SPM, obtained by the Welch method from 50,000 counts (Fig. 2), = 2.4232e-04 m 2 )
After substituting the found estimates Rxx [i], we have:

The following model parameters are defined: a 0 = 11325.9; a 1 = -7090.1; a 2 = 8411.5; As can be seen from (3), the dispersion of the hypothetical white noise here was given = 1, determining instead the gain factor a 0 . The autoregressive estimate of the SPM is constructed by Fourier transform over a sequence of coefficients a 0 , a 1 , a 2 :
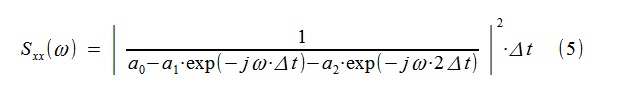

Fig.3. Classical and autoregressive estimation of the “short” process DMA
In the same way, according to an expression similar to (5), the “theoretical” SPM plot was previously constructed, only the model coefficients there, naturally, were taken different (from (2)).
From the graph it is clear that the AR-estimate of the SPM was very close to the theoretically expected. In addition to the graph, there is an opportunity to try to evaluate some of the analytical characteristics of the process and the associated mechanical system. In this case, these are the “poles” of the model, numerically characterizing the frequencies of the “resonant” peaks of the model and the associated “Q-factors”.
From (5) we find the relation for searching for discontinuities of the transfer function of our model using the Laplace transform (replacing jω with λ = -ε + jω):
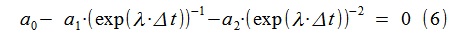
For the obtained AR-model in this way, λ 1,2 = -1.5427 ± j · 10.1514 is calculated, which is very close to the original model used to generate the process
λ 1,2 theor = -1.2500 ± j · 9.9216 (that is, the positions of the resonant peak, respectively, 1.615 Hz (in theory) and 1.579 Hz (determined)).

Fig.4 On the concept of "poles"
A few comments and recommendations in conclusion.
- "Excessive" (too large) order of the AR-model is usually much less dangerous than insufficient, in terms of the risk of obtaining an evaluation of the JMP with gross errors.
- As a rule, AR-modeling makes it possible to quite accurately determine the resonance frequencies jω k and, much less accurately, the widths of the corresponding “peaks” –ε k
- The ARMA model can turn out to be of much smaller order (size) than the AR model, which one seems to be striving to increase the accuracy of the model, according to many sources. However, evaluating the MA-part of the model is much more difficult and may generally include the first step in obtaining a high-order AR-model with a view to its further transformation into the MA-part. In this connection, sources also express an alternative opinion on the expediency of using AR models for spectral estimation purposes, even if they are of a greater order.
- For very short, as well as for non-stationary processes, instead of a matrix of autocorrelation function estimates in (3), the covariances matrix is usually used.
- For a detailed study of the issue of autoregressive spectral assessment, we can recommend S.L. Marple Jr "Digital spectral analysis and its applications", M., Mir, 1990
Source: https://habr.com/ru/post/448078/
All Articles