Design on the basis of "reflection"
Hello. Recently asked the question: "What if ...?". As a result, this theme-idea was born: Design on the basis of "reflection".
I want to share this very idea with you in this publication.

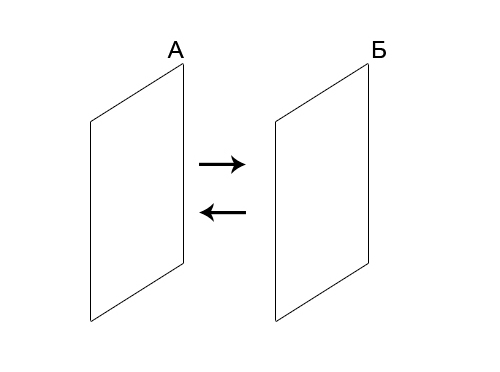
Take two mirrors and set them opposite each other.
')
We divide the reflections into two types: direct (denoted by •) and deep (denoted by °).

Let's turn the mirror “B” with the reflecting side to the mirror “B”, and the mirror “G” with the reflecting side to the mirror “A.”

Now let's imagine that the mirror “B” is translucent and there are three more mirrors behind it: D, E, and G. It can even be said that “B” is a single whole consisting of several parts. And instead of the “G” mirror we will have a vase with flowers, and now “G” will be reflected, but there will be nothing to reflect.

On the reverse side of the mirror “B”, what was reflected in it was reflected: “° D”, “• A” and “• B”. These manifestations will find their direct reflections in D, E and G.
And now let's turn the mirror “D” with the reflecting surface to the mirror “E”.
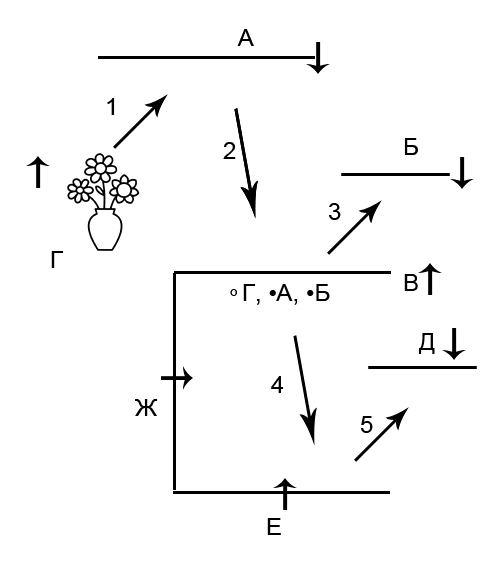
4. "° D" will find its direct reflection "• ° ° D" in the mirror "E". "• A" will find its direct reflection "•• A" in the mirror "E". "• B" will find its direct reflection "•• B" in the mirror "E".
5. “E” will find its direct reflection “• E” in the mirror “D”. “° D” will find its deep reflection “°° G” in the mirror “D”. “• A” will find its deep reflection “° • A” in the mirror “D”. “• B” will find its deep reflection “° • B” in the mirror “D”.
Consider a scheme in which a computer device is simply depicted.

Redraw it.
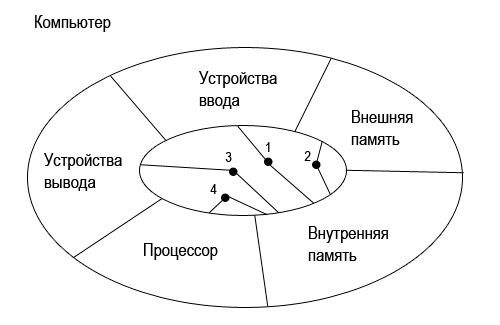
A computer as a single whole system consists of parts: input devices, external memory, output devices, a processor, internal memory. Each of these parts is arranged in its own way, and is separate, because it can be replaced. Also, each of these parts can be considered separately. All parts exist within a single whole (Computer), and in some way interact with each other.

The internal memory has its own kind of structure, it is divided into segments.
All parts of the Computer, interacting with the Internal Memory - specifically refer to the segments of the Memory, but the parts of the Computer have nothing to do with the structures of the Internal Memory.
When considering Internal Memory as a separate part, as a subsystem, some parts of the “Computer” are reflected and manifest in this subsystem on the basis that this subsystem, as a separate part of a more global system, interacts with some parts of this system.
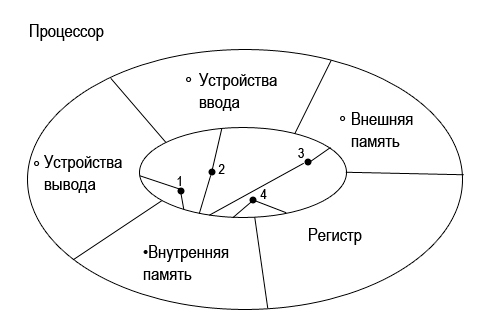
Directly with the processor interacts only internal memory. The remaining parts interact with the processor, but through the internal memory, therefore, they find in it not a direct, but a deep reflection.
Again, the data does not arrive in the entire processor, but in its specific part - the register.
The interaction of parts of the supersystem is also reflected.
In fact, the processor register receives data from the Internal Memory Segment.
Therefore, you can portray

That's all for now. I hope that you are imbued with this idea and understand what I wrote here.
I want to share this very idea with you in this publication.

Let's start
Take two mirrors and set them opposite each other.
')

- Mirror "A" will be reflected in the mirror "B".
- Mirror "B" will be reflected in the mirror "A". In the mirror “A”, everything that is reflected in the mirror “B” will also be reflected. (Similarly, everything that is reflected in the mirror “A” will be reflected in the mirror “B”.)
Types of reflections
We divide the reflections into two types: direct (denoted by •) and deep (denoted by °).
- The mirror “A”, reflected in the mirror “B”, finds in it its direct reflection “• A.”
- Mirror "B", reflected in the mirror "A" finds its direct reflection "• B". Reflecting what was reflected in the mirror “B”, the mirror “A” will find its deep reflection “° A” - in itself.
Now take four mirrors: A, B, C and D

- "A" finds its direct reflection "• A" in B, C and G.
- "B" finds its direct reflection "• B" in A, B and G.
- “C” is directly reflected “• C” in A, B and G.
- “G” finds its direct reflection “• G” in A, B, and B.
Let's turn the mirror “B” with the reflecting side to the mirror “B”, and the mirror “G” with the reflecting side to the mirror “A.”

- The mirror “G” finds its direct reflection “• G” in the mirror “A”.
- The mirror “A” finds its direct reflection “• A” in the mirror “B”. The mirror “G” finds its deep reflection “° D” in the mirror “B”.
- The mirror “B” finds its direct reflection “• C” in “B”. The mirror “A” finds its deep reflection “° A” in the mirror “B”. The mirror “G” finds its deep reflection “°° G” in the mirror “B”.
Now the mirror “G” does not find direct reflections in “C” and “B”, but only the deep ones (“° D” in “C” and “°° D” in “B”) through mirror “A”. In “B” the mirror “B” is reflected, in which the mirror “A” is reflected, and in the mirror “A” the mirror “G” found its direct reflection. Therefore, if we look at what we have in the mirror “B”, we will see: “• C”, “° A” and “°° D”. And, if we look at “C”, we will see: “• A”, “° D” and “• B” because everything works in the opposite direction.
Reflection display
Now let's imagine that the mirror “B” is translucent and there are three more mirrors behind it: D, E, and G. It can even be said that “B” is a single whole consisting of several parts. And instead of the “G” mirror we will have a vase with flowers, and now “G” will be reflected, but there will be nothing to reflect.

On the reverse side of the mirror “B”, what was reflected in it was reflected: “° D”, “• A” and “• B”. These manifestations will find their direct reflections in D, E and G.
- "° D" will find its direct reflection "• ° ° D" in D, E, and J.
- “• A” will find its direct reflection “•• A” in D, E, and J.
- “• B” will find its direct reflection “•• B” in D, E, and J.
And now let's turn the mirror “D” with the reflecting surface to the mirror “E”.

4. "° D" will find its direct reflection "• ° ° D" in the mirror "E". "• A" will find its direct reflection "•• A" in the mirror "E". "• B" will find its direct reflection "•• B" in the mirror "E".
5. “E” will find its direct reflection “• E” in the mirror “D”. “° D” will find its deep reflection “°° G” in the mirror “D”. “• A” will find its deep reflection “° • A” in the mirror “D”. “• B” will find its deep reflection “° • B” in the mirror “D”.
If you start this process in the opposite direction, then the mirror “D” will find its direct reflection “• D” in the mirror “E”, the deep reflection “° D” in “B”, then “° D” will find direct reflection “• ° D "In" A ". Well, in "G" is no longer reflected, because it is not a mirror, but a vase in flowers.
What is the practical use of all this?
Consider a scheme in which a computer device is simply depicted.

Redraw it.

A computer as a single whole system consists of parts: input devices, external memory, output devices, a processor, internal memory. Each of these parts is arranged in its own way, and is separate, because it can be replaced. Also, each of these parts can be considered separately. All parts exist within a single whole (Computer), and in some way interact with each other.
- Input devices interact with internal memory.
- External memory interacts with internal memory.
- Output devices interact with internal memory.
- The processor interacts with the internal memory.
Consider separately the part of the Computer "Internal Memory" (RAM).

The internal memory has its own kind of structure, it is divided into segments.
All parts of the Computer, interacting with the Internal Memory - specifically refer to the segments of the Memory, but the parts of the Computer have nothing to do with the structures of the Internal Memory.
When considering Internal Memory as a separate part, as a subsystem, some parts of the “Computer” are reflected and manifest in this subsystem on the basis that this subsystem, as a separate part of a more global system, interacts with some parts of this system.
- Input devices found their direct reflection “• Input devices” in the Internal Memory, based on direct interaction with the Internal Memory. Appearing in this system as “Input Devices” interact with the Internal Memory Segments.
- "• External Memory" interacts with internal memory segments
- "• Output devices" interact with internal memory segments.
- "• Processor" interacts with internal memory segments
Consider the part of the Computer - "Processor".

Directly with the processor interacts only internal memory. The remaining parts interact with the processor, but through the internal memory, therefore, they find in it not a direct, but a deep reflection.
Again, the data does not arrive in the entire processor, but in its specific part - the register.
The interaction of parts of the supersystem is also reflected.
- "° Output Devices" interacts with internal memory.
- "° Input Device" interacts with internal memory.
- “° External Memory” interacts with internal memory.
- "• Internal memory" interacts with the processor register.
In fact, the processor register receives data from the Internal Memory Segment.
Therefore, you can portray

- "° Output Device" interacts with the Internal Memory segment. The Segment itself (RAM) is not part of this structure and is not in it. Appearing in a single whole "Computer" as "• Segment (RAM)", he found a direct reflection of the "•• Segment (RAM)" in the "processor" based on the interaction of RAM with the processor.
- "° Input devices" interact with "•• Segment (RAM)".
- "° External memory" interacts with the "•• Segment (RAM)".
- "•• Segment (RAM)" interacts with the processor register. From one data to another and back.
An example of practical use in parsing Games
Let's analyze and design a part of the Game. This example is somewhat different from the example with mirrors.
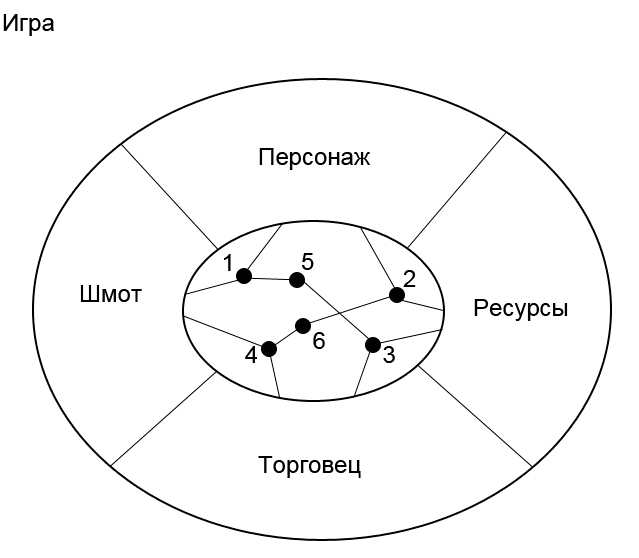
A “game” is a single unit that consists of: Character, Resources, Merchant, and Shemot. All of the above are separate parts, but existing within a single whole.

In “•• Shemot”, “Image of the character” and “° Merchant’s resources” are directly reflected.
“•• Shemot” is a separate, existing in itself part of the Game (“Shemot”), which first found its direct reflection “• Shemot” in the part of the game - “Character”, based on the interaction with this part. Then, being a part of “Character”, not its original part, but acquired, which found its manifestation (on the basis of interaction with this part) - “• Shemot” found its direct reflection “•• Shemot” in the original parts of “Character”: Inventory and Backpack.
There, in the Character and Inventory, • Shemote and •• Shemot interact with the merchant's Resources and merchant resources.
It is not so easy to take and exchange part of the game "Shemot" for the part of the game "Resources." You can not just change the character's gear for character resources. But the character's gear can be exchanged for the resources of the merchant. That is, these parts must first be reflected in something and manifest there, and only then be exchanged in the interaction of two parts (Character, Merchant) in which they are reflected. But do not dwell on this moment.
A “game” is a single unit that consists of: Character, Resources, Merchant, and Shemot. All of the above are separate parts, but existing within a single whole.

- A character may have a gear.
- A character may have resources.
- The merchant has a gear.
- The merchant has resources.
- The character's gear can be exchanged for merchant resources. (Shemot is first directly reflected in the character, then deep in the merchant and deep in the resources)
- Merchant's gear can be exchanged for character resources.
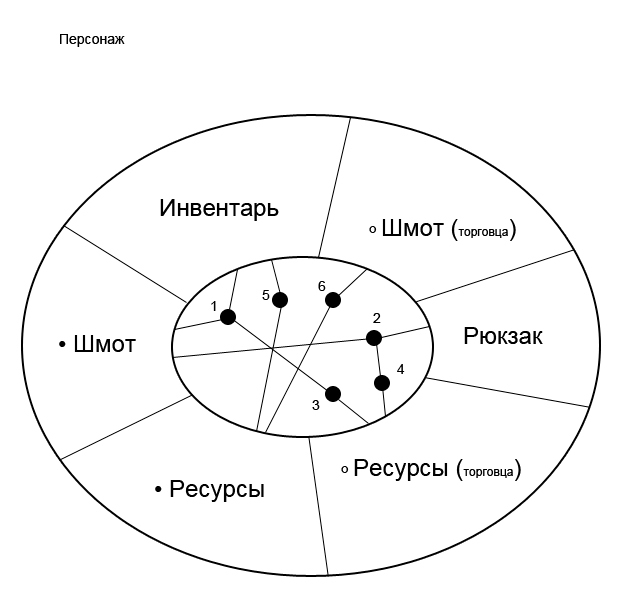
Recall the translucent mirror “B” and consider as a whole one of the parts of the Game - “Character”

In the character, we can observe parts of the “character”: inventory and a backpack (as mirrors D, E, and M in a mirror “B”) and parts reflected in the “Character” part based on direct or deep interaction with this part within a single of the whole ("Game").
- "• Shemot" may be in the inventory of the character.
- "• Shemot" may be in the character's backpack.
- "• Sheepskin" from the character's inventory can be exchanged for "merchant resources".
- “• Shemot” from the character’s backpack can be exchanged for “merchant resources”.
- "• Resources" of the character are displayed in the inventory of the character.
- "• Resources" of the character can be exchanged for "° Merchant Sheet".
Let's go even deeper into inventory

- "°° Merchant's Items" can be exchanged for "•• Character Resources". In fact, the previous time, “° Merchant's Sheet” was not reflected in the Inventory, but it was reflected in “Resources”, and “• Resources” were directly reflected in “•• Resources” in “Inventory”. On the basis of this, “° Merchant's Items” found its deep reflection of the “°° Merchant's Items” in “Inventory”.
- "•• Shemot" in the inventory (worn) character affects the appearance of the image of the character, which is shown in the inventory of the character.
- “•• Shemot” in the character’s inventory can be traded for “Merchant Resources”.
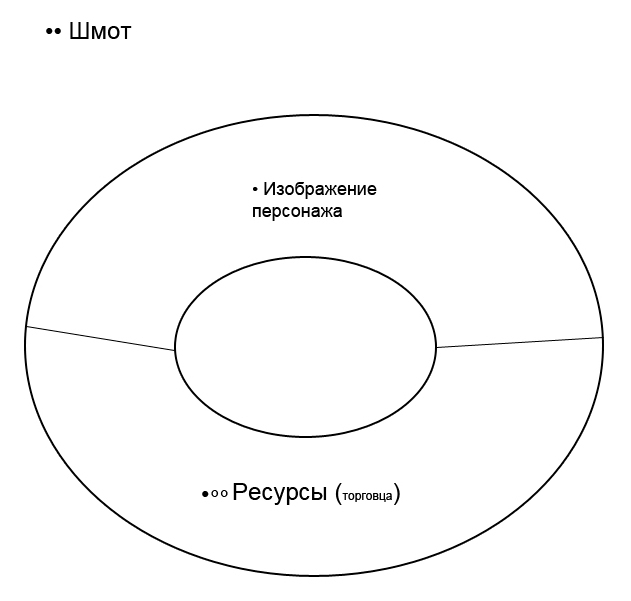
Look at the "•• Shemot"

In “•• Shemot”, “Image of the character” and “° Merchant’s resources” are directly reflected.
“•• Shemot” is a separate, existing in itself part of the Game (“Shemot”), which first found its direct reflection “• Shemot” in the part of the game - “Character”, based on the interaction with this part. Then, being a part of “Character”, not its original part, but acquired, which found its manifestation (on the basis of interaction with this part) - “• Shemot” found its direct reflection “•• Shemot” in the original parts of “Character”: Inventory and Backpack.
There, in the Character and Inventory, • Shemote and •• Shemot interact with the merchant's Resources and merchant resources.
Exchange Items for Resources
It is not so easy to take and exchange part of the game "Shemot" for the part of the game "Resources." You can not just change the character's gear for character resources. But the character's gear can be exchanged for the resources of the merchant. That is, these parts must first be reflected in something and manifest there, and only then be exchanged in the interaction of two parts (Character, Merchant) in which they are reflected. But do not dwell on this moment.
That's all for now. I hope that you are imbued with this idea and understand what I wrote here.
Source: https://habr.com/ru/post/447924/
All Articles