Photos from rough sketches: how exactly does the NVIDIA GauGAN neural network work?
Last month, NVIDIA unveiled a new application at NVIDIA GTC 2019 that turns simple colored balls drawn by the user into gorgeous photo-realistic images.
The application is built on the technology of generative-competitive networks (GAN), which is based on in-depth training. NVIDIA itself calls it GauGAN - a pun intended as a reference to artist Paul Gauguin. At the core of the GauGAN functionality is the new SPADE algorithm.
In this article I will explain how this engineering masterpiece works. And in order to attract as many interested readers as possible, I will try to give a detailed description of how convolutional neural networks work. Since SPADE is a generative and adversary network, I will tell you more about them. But if you are already familiar with this term, you can go directly to the section “Image-to-image translation”.
')
Let's begin to understand: in most modern applications of deep learning, the neural discriminant type (discriminator) is used, and SPADE is a generative neural network (generator).
The discriminator is engaged in the classification of input data. For example, an image classifier is a discriminator that takes an image and selects one suitable class label, for example, defines an image as “dog”, “car” or “traffic light”, that is, selects a label that fully describes the image. The output obtained by the classifier is usually represented as a vector of numbers. v where v i Is a number from 0 to 1, expressing the network’s confidence in the image belonging to the selected one i class.
A discriminator can also make a whole list of classifications. It can classify each pixel of an image as belonging to the class of “people” or “machines” (the so-called “semantic segmentation”).

The categorizer takes an image with 3 channels (red, green and blue) and matches it with a vector of confidence in every possible class that an image can represent.
Since the connection between an image and its class is very complex, neural networks pass it through a stack of multiple layers, each of which processes it a little and transfers its output to the next level of interpretation.
A generative network like SPADE receives a data set and seeks to create new original data that looks as if it belongs to this data class. In this case, the data can be any: sounds, language or something else, but we will focus on the images. In general, data entry into such a network is simply a vector of random numbers, with each of the possible sets of input data creating its own image.
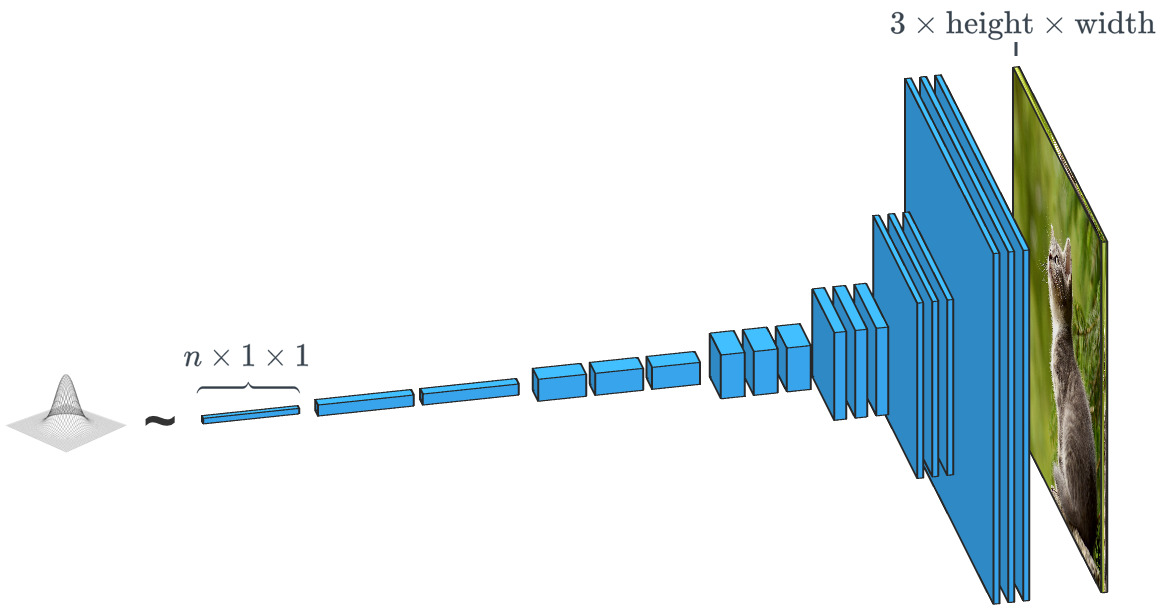
The generator based on a random input vector works in fact the opposite of the image classifier. In the “conditional class” generators, the input vector is, in fact, a vector of a whole class of data.
As we have seen, SPADE uses much more than just a “random vector”. The system is guided by a peculiar drawing, which is called a “segmentation map”. The latter indicates what and where to post. SPADE conducts a process inverse to the semantic segmentation mentioned above. In general, a discriminatory task that translates one type of data into another has a similar task, but follows a different, unaccustomed way.
Modern generators and discriminators typically use convolutional networks to process their data. For a more complete acquaintance with convolutional neural networks (CNNs), see the post Uzhval Karna or the work of Andrey Karpati .
There is one important difference between the classifier and the image generator, and it lies in how they change the size of the image during its processing. The image classifier should reduce it until the image loses all spatial information and only classes remain. This can be achieved by merging the layers, or through the use of convolutional networks through which individual pixels are passed. The generator, on the other hand, creates an image using the inverse “convolution” process, called convolutional transposition. It is often confused with "deconvolution" or "reverse convolution . "
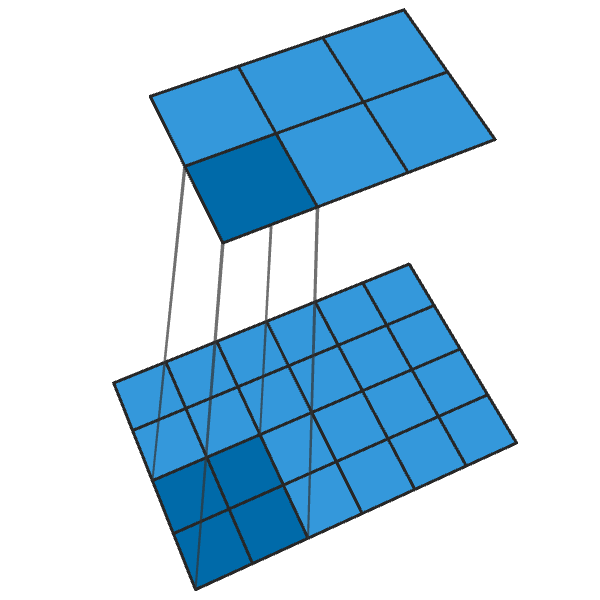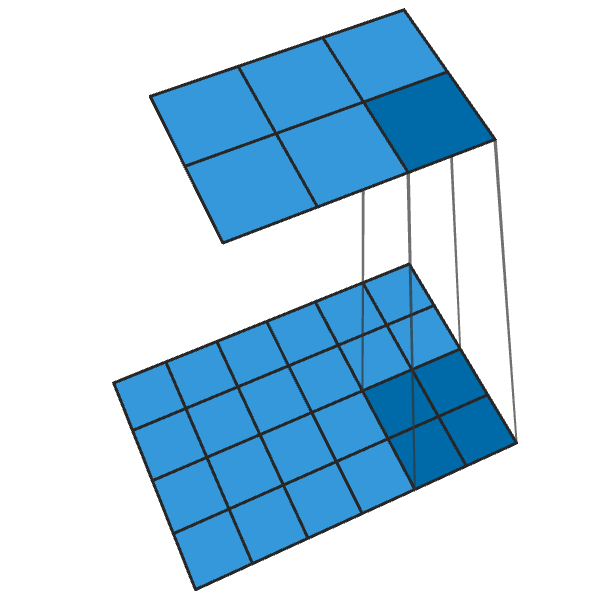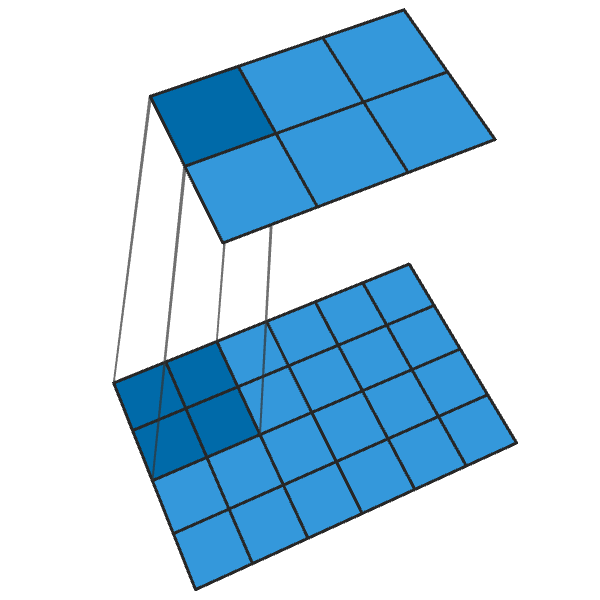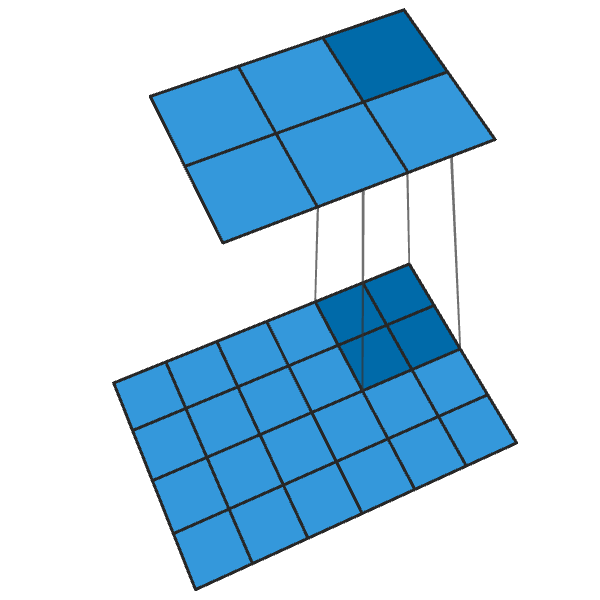
Regular convolution of 2x2 in increments of "2" turns each block of 2x2 into one point, reducing the output dimensions by 1/2.

Transposed convolution of 2x2 with step “2” generates a 2x2 block from each point, increasing the output dimensions by 2 times.
Theoretically, a convolutional neural network can generate images in the manner described above. But how do we train it? That is, if we take into account the set of input data-images, how can we adjust the parameters of the generator (in our case SPADE) to create new images that look as if they correspond to the proposed data set?
For this, it is necessary to make a comparison with image classifiers, where each of them has the correct class label. Knowing the network prediction vector and the correct class, we can use the backpropagation algorithm to determine the network update parameters. This is necessary to increase its accuracy in determining the desired class and reduce the influence of other classes.
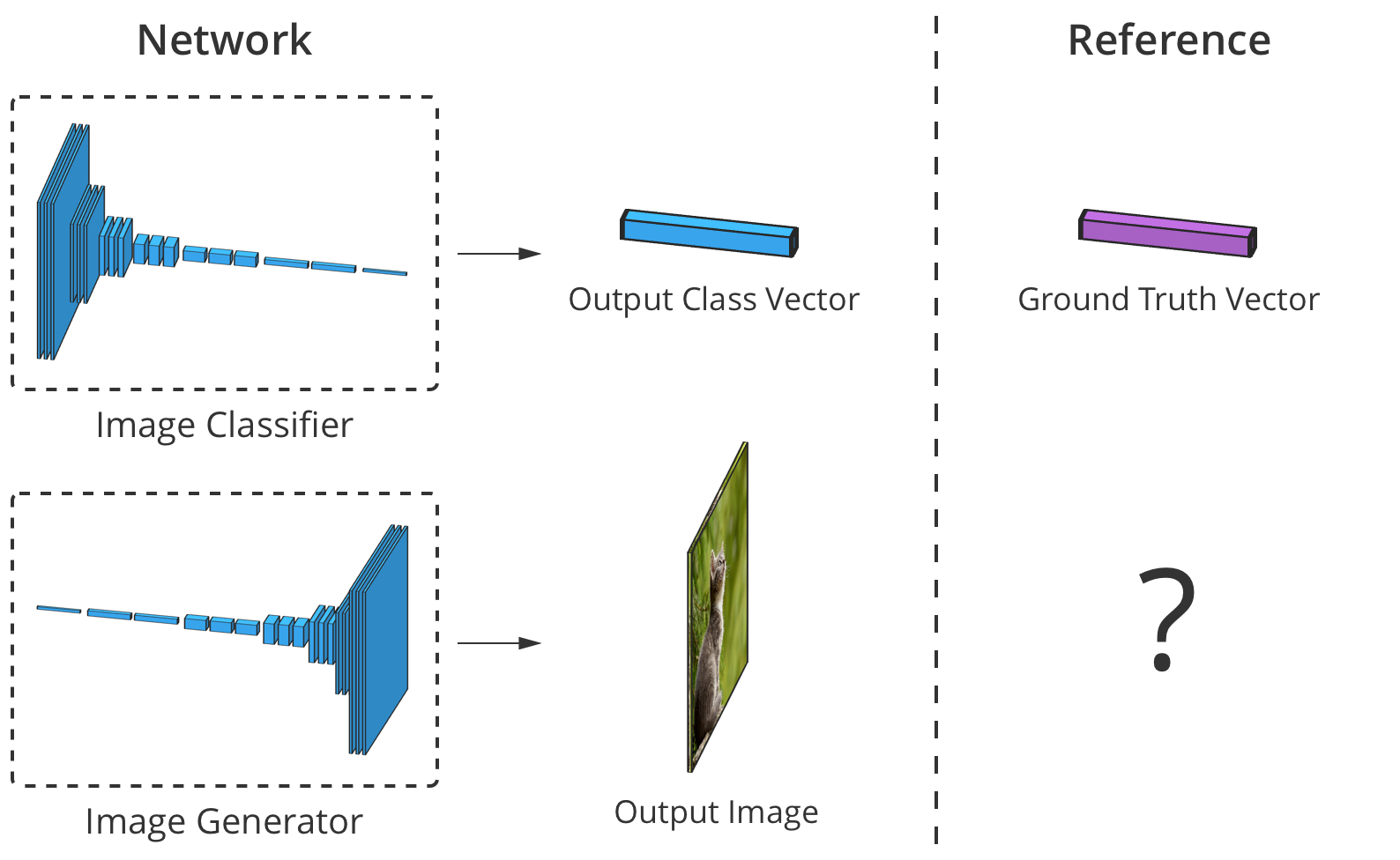
The accuracy of the image classifier can be assessed by comparing its output element by element with the correct class vector. But for generators there is no “right” output image.
The problem is that when the generator creates an image, there are no “correct” values for each pixel (we cannot compare the result, as in the case of the classifier on a previously prepared base, - approx. Lane). Theoretically, any image that looks plausible and looks like target data is valid, even if its pixel values are very different from real images.
So, how can we tell the generator in which pixels it should change its output, and how can it create more realistic images (i.e., how to give an “error signal”)? Researchers have thought a lot about this issue, and in fact it is quite difficult. Most ideas, such as calculating some average "distance" to real images, give low-quality blurry pictures.
Ideally, we could “measure” how realistic the generated images look by using the “high level” concept, such as “How difficult is it to distinguish this image from the real one?” ...
That is what was realized in the framework of the work of Goodfellow et al., 2014 . The idea is to generate images using two neural networks instead of one: one network -
the generator, the second - the image classifier (discriminator). The discriminator’s task is to distinguish the output images of the generator from the real images from the primary data set (the classes of these images are marked as “fake” and “real”). The job of the generator is to trick the discriminator by creating images that most closely resemble the images in the data set. It can be said that the generator and the discriminator are opponents in this process. Hence the name: generative-adversary network .
Generative-adversary network based on random vector input. In this example, one of the generator outputs tries to trick the discriminator when selecting the “real” image.
How does this help us? Now we can use an error message based solely on discriminator prediction: a value from 0 (“fake”) to 1 (“real”). Since the discriminator is a neural network, we can share its conclusions about errors and the image generator. That is, the discriminator can tell the generator where and how he should correct his images in order to better “deceive” the discriminator (i.e., how to increase the realism of his images).
In the process of learning to find fake images, the discriminator provides the generator with the best and best feedback on how the latter can improve its work. Thus, the discriminator performs the “learn a loss” function for the generator.
The GAN considered by us in its work follows the logic described above. His discriminator D analyzes the image x and gets value D ( x ) from 0 to 1, which reflects his degree of confidence in whether this is a real image, or forged by a generator. His generator G gets a random vector of normally distributed numbers Z and displays the image G ( z ) which may be deceived by the discriminator (in fact, this image D ( G ( z ) ) )
One of the questions that we didn’t discuss is how GAN is taught and what loss function developers use to measure network performance. In the general case, the loss function should increase as the discriminator learns and decrease as the generator learns. The loss function of the original GAN used the following two parameters. The first -
represents the degree of how often the discriminator correctly classifies real images as real. The second is how well the discriminator detects fake images:
$ inline $ \ begin {equation *} \ mathcal {L} _ \ text {GAN} (D, G) = \ underbrace {E _ {\ vec {x} \ sim p_ \ text {data}} [\ log D ( \ vec {x})]} _ {\ text {accuracy on real images}} + \ underbrace {E _ {\ vec {z} \ sim \ mathcal {N}} [\ log (1 - D (G (\ vec {z}))]} _ {\ text {accuracy on fakes}} \ end {equation *} $ inline $
Discriminator D derives his claim that the image is real. It makes sense, since L o g D ( x ) increases when the discriminator considers x to be real. When the discriminator detects fake images better, the value of the expression increases. L o g ( 1 - d ( g ( z ) ) (begins to strive for 1), since D ( G ( z ) ) will aim for 0.
In practice, we estimate accuracy using whole batches of images. We take a lot (but not all) of real images. x and many random vectors Z to get averaged numbers using the formula above. Then we select common errors and data set.
Over time, this leads to interesting results:

Goodfellow GAN that mimics the MNIST, TFD and CIFAR-10 data sets. Contour images are closest in the data set to adjacent counterfeits.
All this was fantastic just 4.5 years ago. Fortunately, as shown by SPADE and other networks, machine learning continues to progress rapidly.
Generative-competitive networks are notorious for their complexity in the preparation and instability of work. One of the problems is that if the generator is too far ahead of the discriminator in the pace of learning, then its selection of images is narrowed down to specifically those that help it to deceive the discriminator. In fact, as a result, generator training comes down to the creation of a single universal image to deceive the discriminator. This problem is called “collapse mode”.

GAN collapse mode is similar to Goodfellow's. Note that many of these bedroom images look very similar to each other. A source
Another problem is that when the generator effectively deceives the discriminator D ( g ( z ) ) , it operates with a very small gradient, therefore mathcalL textGANG( vecz) can not get enough data to find the true answer, in which this image would look more realistic.
The efforts of researchers to solve these problems were mainly aimed at changing the structure of the loss function. One of the simple changes proposed by Xudong Mao et al., 2016 , is to replace the loss function mathcalL textGAN for a couple of simple functions V textLSGAN which are based on smaller squares. This leads to a stabilization of the training process, obtaining higher-quality images and a lower chance of collapse using continuous gradients.
Another problem faced by researchers is the difficulty of obtaining high-resolution images, partly because the more detailed image gives the discriminator more information for detecting fake images. Modern GANs begin to train the network with low-resolution images and gradually add more and more layers until the desired image size is reached.

Gradually adding higher resolution layers during GAN training significantly improves the stability of the entire process, as well as the speed and quality of the resulting image.
So far we have been talking about how to generate images from random sets of input data. But SPADE doesn't just use random data. This network uses an image called a segmentation map: it assigns each pixel a class of material (for example, grass, wood, water, stone, sky). From this map image, SPADE generates what looks like a photo. This is called the "Image-to-image broadcast".

Six different types of Image-to-image broadcasting, demonstrated by the pix2pix network. Pix2pix is the forerunner of two networks, which we will examine further: pix2pixHD and SPADE.
In order for the generator to learn this approach, it needs a set of segmentation maps and corresponding photos. We modify the GAN architecture so that both the generator and the discriminator receive a segmentation map. The generator, of course, needs a map in order to know which way to draw. It is also necessary for the discriminator to make sure that the generator places the right things in the right places.
During training, the generator learns not to plant grass where the sky is indicated on the segmentation map, because otherwise the discriminator will easily identify the fake image, and so on.
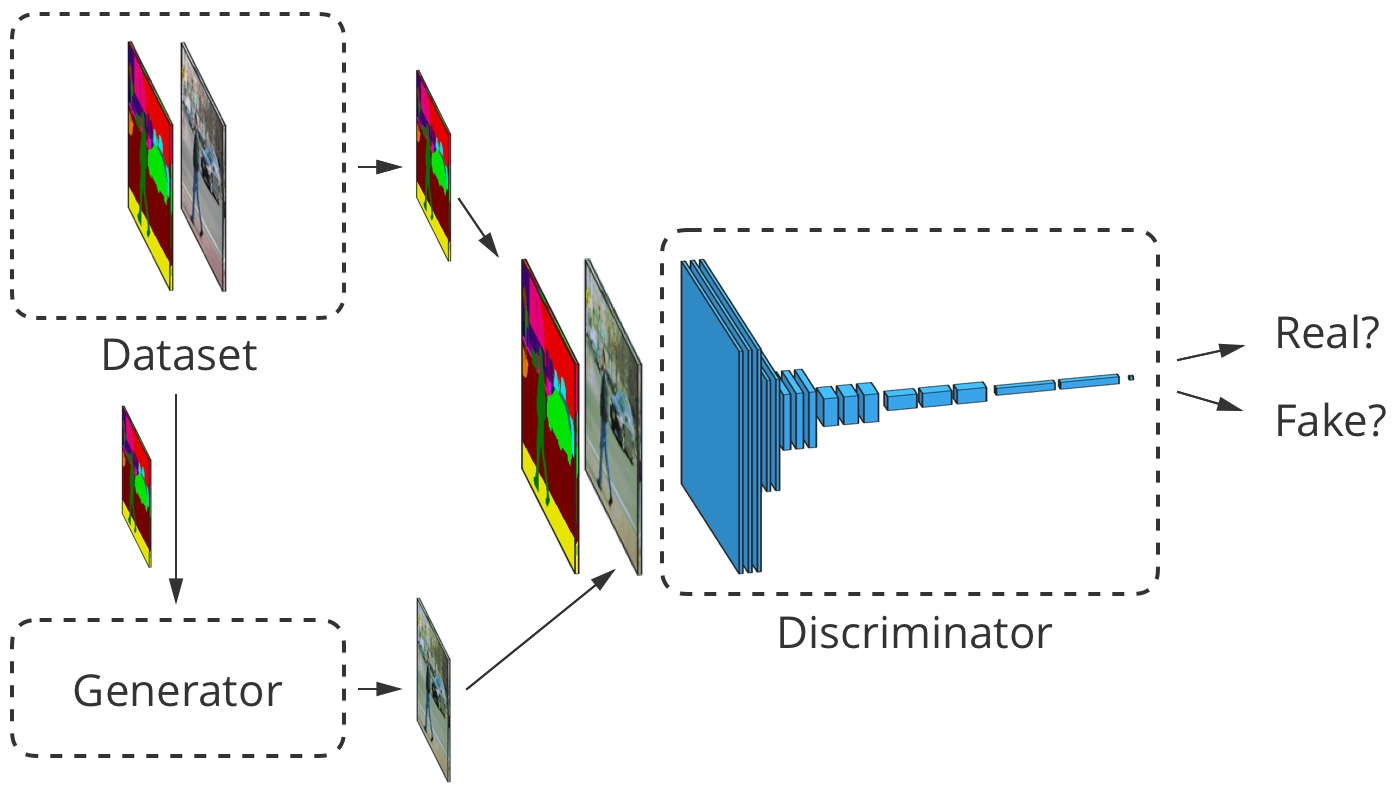
For image-to-image translation, the input image is received by both the generator and the discriminator. The discriminator additionally receives either the generator output data or the true output from the training data set. Example
Let's look at the real image-to-image translator: pix2pixHD . By the way, SPADE is designed mostly in the image and likeness of pix2pixHD.
For the image-to-image translator, our generator creates an image and takes it as an input. We could just use a map of convolutional layers, but since convolutional layers only combine values in small areas, we need too many layers to transmit image information in high resolution.
pix2pixHD solves this problem more efficiently with the help of the “Encoder”, which reduces the scale of the input image, followed by the “Decoder”, which increases the scale to obtain the output image. As we will soon see, SPADE has a more elegant solution that does not require an encoder.

The pix2pixHD network scheme is at the “high” level. “Residual” blocks and “+ operation” refer to the “skip connections” technology of the Residual neural network . There are skip blocks in the network that correspond to each other in the encoder and decoder.
Almost all modern convolutional neural networks use packet normalization or one of its analogues to speed up and stabilize the training process. Activating each channel shifts the mean to 0 and the standard deviation to 1 before the pair of channel parameters beta and gamma allow them to denormalize again.
y= fracx− mathrmE[x] sqrt mathrmVar[x]+ epsilon∗ gamma+ beta
Unfortunately, packet normalization damages the generators, making it difficult for the network to implement some types of image processing. Instead of normalizing a batch of images, pix2pixHD uses the normalization standard , which normalizes each image separately.
Modern GANs, such as pix2pixHD and SPADE, measure the realism of their output images in a slightly different way than was described for the original design of generative-contention networks.
To solve the problem of generating high-resolution images, pix2pixHD uses three discriminators of the same structure, each of which receives an output image at a different scale (normal size, reduced by 2 times and reduced by 4 times).
To determine its loss function, pix2pixHD uses V textLSGAN and also includes another element designed to make the generator outputs more realistic (regardless of whether it helps to deceive the discriminator). This item m a t h c a l L t e x t F M is called “feature matching” - it causes the generator to make the distribution of layers when simulating discrimination the same between real data and generator outputs, minimizing L 1 D i s t a n c e between them.
So, optimization is as follows:
where losses are summed by three discriminatory factors and coefficient l a m b d a = 10 which controls the priority of both elements.

pix2pixHD uses a segmentation map made up of a real bedroom (on the left in each example) to create a fake bedroom (on the right).
Although discriminators reduce the scale of the image until the entire image is disassembled, they stop at “spots” measuring 70 × 70 (at appropriate scales). Then they simply summarize all the values of these “spots” for the entire image.
And this approach works great because the function m a t h c a l L t e x t F M makes sure that the image looks realistic in high resolution, and V t e x t L S G A N only required for checking small parts. This approach also has additional advantages in the form of network acceleration, reducing the number of parameters used and the possibility of using it to generate images of any size.

pix2pixHD generates photorealistic images with appropriate grimaces from simple sketches of faces. Each example shows a real image from the CelebA dataset on the left, a sketch of this celebrity's facial expression in the form of a sketch and the image created from this data on the right.
These results are incredible, but we can do better. It turns out that pix2pixHD loses a lot in one important aspect.
Consider what pix2pixHD does with single-entry, for example, with a map that has grass everywhere. Since the entrance is spatially uniform, the outputs of the first convolutional layer are also the same. Then normalization of instances “normalizes” all (identical) values for each channel in the image and returns 0 as a conclusion for all of them. The β-parameter can shift this value from zero, but the fact remains: the output will no longer depend on whether the input is “grass”, “sky”, “water” or something else.

In pix2pixHD, instance normalization tends to ignore information from the segmentation map. For images consisting of one class, the network generates the same image independently of this class itself.
And the solution to this problem is the main feature of the SPADE design.
Finally, we have reached a fundamentally new level in the creation of images from segmentation maps: spatial-adaptive (de) normalization (SPADE).
The idea behind SPADE is to prevent the semantic information from being lost in the network, allowing the segmentation map to control the normalization parameters γ, as well as β, locally, at the level of each individual layer. Instead of using only one pair of parameters for each channel, they are calculated for each spatial point by submitting a downsampled segmentation map through 2 convolutional layers.
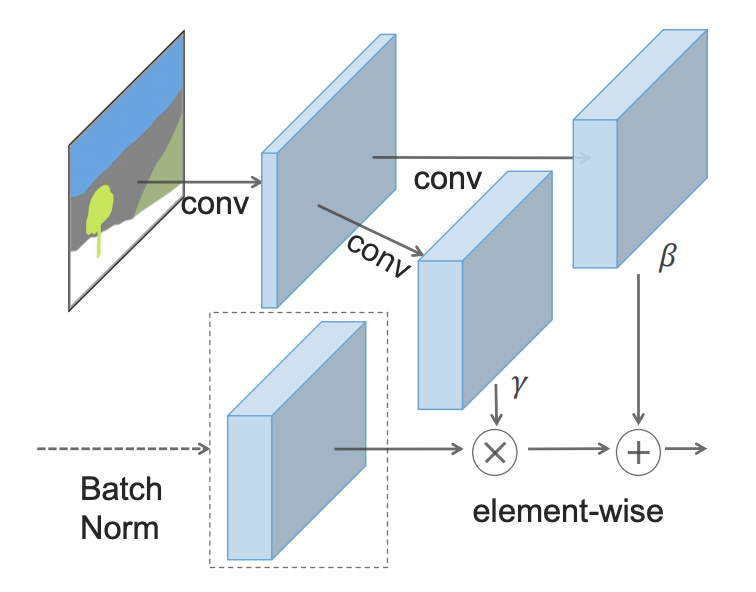
Instead of rolling the segmentation map onto the first layer, SPADE uses its downsampled versions to modulate the normalized output for each layer.
The SPADE generator integrates the entire structure into small “residual blocks” that fit between the upsampling layers (transposed convolution):

SPADE high-level generator circuit versus pix2pixHD
Now that the segmentation map is being fed from the inside of the network, there is no need to use it as input for the first layer. Instead, we can return to the original GAN scheme, which used a random vector as input. This gives us an additional opportunity to generate different images from one segmentation map (“multimodal synthesis”). It also makes unnecessary the entire pix2pixHD “encoder”, and this is a serious simplification.
SPADE uses the same loss function as pix2pixHD, but with one change: instead of squaring the values V t e x t L S G A N it uses hinge loss .
With these changes we get great results:

Here the results of SPADE are compared with the results of pix2pixHD
Let's think about how SPADE can show such results. In the example below, we have a tree. GauGAN uses one "tree" class to represent both the trunk and the leaves of the tree. However, somehow SPADE finds out that the narrow part at the bottom of the “tree” is the trunk and should be brown, while the large drop from above should be foliage.
The down-sampled segmentation that SPADE uses to modulate each layer provides similar “intuitive” recognition.
You may notice that the tree trunk continues in the part of the crown, which refers to the "foliage". So how does SPADE understand where to place part of the trunk there, and where is the foliage? After all, judging by the 5x5 map, there should be just a “tree” there.
The answer is that the area shown can receive information from lower resolution layers, where a 5x5 block contains the entire tree. Each subsequent convolutional layer also provides some movement of information in the image, which gives a more complete picture.
SPADE allows the segmentation map to directly modulate each layer, but this does not hinder the process of connected information distribution between layers, as it happens, for example, in pix2pixHD. This prevents the loss of semantic information, since it is updated in each subsequent layer at the expense of the previous one.
In SPADE, there is another magical solution - the ability to generate an image in a given style (for example, lighting, weather, time of year).

SPADE can generate several different images on the basis of a single segmentation map, mimicking a given style.
It works like this: we skip the images through the encoder and train it to set the generator vectors Z which in turn will generate similar images. After the encoder has been trained, we replace the corresponding segmentation maps with arbitrary ones, and the SPADE generator creates images that correspond to the new maps, but in the style of the provided images based on previously received training.
Since the generator usually expects to receive a sample on the basis of a multidimensional normal distribution, in order to obtain realistic images, we must train the encoder to derive values with a similar distribution. In fact, this is the idea of variational auto-encoders , which is explained by Yoel Zeldes .
This is how SPADE / GaiGAN functions. I hope this article has satisfied your curiosity about how the new NVIDIA system works. You can contact me via Twitter @AdamDanielKin or by email adam@AdamDKing.com.
The application is built on the technology of generative-competitive networks (GAN), which is based on in-depth training. NVIDIA itself calls it GauGAN - a pun intended as a reference to artist Paul Gauguin. At the core of the GauGAN functionality is the new SPADE algorithm.
In this article I will explain how this engineering masterpiece works. And in order to attract as many interested readers as possible, I will try to give a detailed description of how convolutional neural networks work. Since SPADE is a generative and adversary network, I will tell you more about them. But if you are already familiar with this term, you can go directly to the section “Image-to-image translation”.
')
Image generation
Let's begin to understand: in most modern applications of deep learning, the neural discriminant type (discriminator) is used, and SPADE is a generative neural network (generator).
Discriminators
The discriminator is engaged in the classification of input data. For example, an image classifier is a discriminator that takes an image and selects one suitable class label, for example, defines an image as “dog”, “car” or “traffic light”, that is, selects a label that fully describes the image. The output obtained by the classifier is usually represented as a vector of numbers. v where v i Is a number from 0 to 1, expressing the network’s confidence in the image belonging to the selected one i class.
A discriminator can also make a whole list of classifications. It can classify each pixel of an image as belonging to the class of “people” or “machines” (the so-called “semantic segmentation”).

The categorizer takes an image with 3 channels (red, green and blue) and matches it with a vector of confidence in every possible class that an image can represent.
Since the connection between an image and its class is very complex, neural networks pass it through a stack of multiple layers, each of which processes it a little and transfers its output to the next level of interpretation.
Generators
A generative network like SPADE receives a data set and seeks to create new original data that looks as if it belongs to this data class. In this case, the data can be any: sounds, language or something else, but we will focus on the images. In general, data entry into such a network is simply a vector of random numbers, with each of the possible sets of input data creating its own image.

The generator based on a random input vector works in fact the opposite of the image classifier. In the “conditional class” generators, the input vector is, in fact, a vector of a whole class of data.
As we have seen, SPADE uses much more than just a “random vector”. The system is guided by a peculiar drawing, which is called a “segmentation map”. The latter indicates what and where to post. SPADE conducts a process inverse to the semantic segmentation mentioned above. In general, a discriminatory task that translates one type of data into another has a similar task, but follows a different, unaccustomed way.
Modern generators and discriminators typically use convolutional networks to process their data. For a more complete acquaintance with convolutional neural networks (CNNs), see the post Uzhval Karna or the work of Andrey Karpati .
There is one important difference between the classifier and the image generator, and it lies in how they change the size of the image during its processing. The image classifier should reduce it until the image loses all spatial information and only classes remain. This can be achieved by merging the layers, or through the use of convolutional networks through which individual pixels are passed. The generator, on the other hand, creates an image using the inverse “convolution” process, called convolutional transposition. It is often confused with "deconvolution" or "reverse convolution . "

Regular convolution of 2x2 in increments of "2" turns each block of 2x2 into one point, reducing the output dimensions by 1/2.

Transposed convolution of 2x2 with step “2” generates a 2x2 block from each point, increasing the output dimensions by 2 times.
Generator training
Theoretically, a convolutional neural network can generate images in the manner described above. But how do we train it? That is, if we take into account the set of input data-images, how can we adjust the parameters of the generator (in our case SPADE) to create new images that look as if they correspond to the proposed data set?
For this, it is necessary to make a comparison with image classifiers, where each of them has the correct class label. Knowing the network prediction vector and the correct class, we can use the backpropagation algorithm to determine the network update parameters. This is necessary to increase its accuracy in determining the desired class and reduce the influence of other classes.

The accuracy of the image classifier can be assessed by comparing its output element by element with the correct class vector. But for generators there is no “right” output image.
The problem is that when the generator creates an image, there are no “correct” values for each pixel (we cannot compare the result, as in the case of the classifier on a previously prepared base, - approx. Lane). Theoretically, any image that looks plausible and looks like target data is valid, even if its pixel values are very different from real images.
So, how can we tell the generator in which pixels it should change its output, and how can it create more realistic images (i.e., how to give an “error signal”)? Researchers have thought a lot about this issue, and in fact it is quite difficult. Most ideas, such as calculating some average "distance" to real images, give low-quality blurry pictures.
Ideally, we could “measure” how realistic the generated images look by using the “high level” concept, such as “How difficult is it to distinguish this image from the real one?” ...
Generative competitive networks
That is what was realized in the framework of the work of Goodfellow et al., 2014 . The idea is to generate images using two neural networks instead of one: one network -
the generator, the second - the image classifier (discriminator). The discriminator’s task is to distinguish the output images of the generator from the real images from the primary data set (the classes of these images are marked as “fake” and “real”). The job of the generator is to trick the discriminator by creating images that most closely resemble the images in the data set. It can be said that the generator and the discriminator are opponents in this process. Hence the name: generative-adversary network .
Generative-adversary network based on random vector input. In this example, one of the generator outputs tries to trick the discriminator when selecting the “real” image.
How does this help us? Now we can use an error message based solely on discriminator prediction: a value from 0 (“fake”) to 1 (“real”). Since the discriminator is a neural network, we can share its conclusions about errors and the image generator. That is, the discriminator can tell the generator where and how he should correct his images in order to better “deceive” the discriminator (i.e., how to increase the realism of his images).
In the process of learning to find fake images, the discriminator provides the generator with the best and best feedback on how the latter can improve its work. Thus, the discriminator performs the “learn a loss” function for the generator.
"Nice Small" GAN
The GAN considered by us in its work follows the logic described above. His discriminator D analyzes the image x and gets value D ( x ) from 0 to 1, which reflects his degree of confidence in whether this is a real image, or forged by a generator. His generator G gets a random vector of normally distributed numbers Z and displays the image G ( z ) which may be deceived by the discriminator (in fact, this image D ( G ( z ) ) )
One of the questions that we didn’t discuss is how GAN is taught and what loss function developers use to measure network performance. In the general case, the loss function should increase as the discriminator learns and decrease as the generator learns. The loss function of the original GAN used the following two parameters. The first -
represents the degree of how often the discriminator correctly classifies real images as real. The second is how well the discriminator detects fake images:
$ inline $ \ begin {equation *} \ mathcal {L} _ \ text {GAN} (D, G) = \ underbrace {E _ {\ vec {x} \ sim p_ \ text {data}} [\ log D ( \ vec {x})]} _ {\ text {accuracy on real images}} + \ underbrace {E _ {\ vec {z} \ sim \ mathcal {N}} [\ log (1 - D (G (\ vec {z}))]} _ {\ text {accuracy on fakes}} \ end {equation *} $ inline $
Discriminator D derives his claim that the image is real. It makes sense, since L o g D ( x ) increases when the discriminator considers x to be real. When the discriminator detects fake images better, the value of the expression increases. L o g ( 1 - d ( g ( z ) ) (begins to strive for 1), since D ( G ( z ) ) will aim for 0.
In practice, we estimate accuracy using whole batches of images. We take a lot (but not all) of real images. x and many random vectors Z to get averaged numbers using the formula above. Then we select common errors and data set.
Over time, this leads to interesting results:

Goodfellow GAN that mimics the MNIST, TFD and CIFAR-10 data sets. Contour images are closest in the data set to adjacent counterfeits.
All this was fantastic just 4.5 years ago. Fortunately, as shown by SPADE and other networks, machine learning continues to progress rapidly.
Workout problems
Generative-competitive networks are notorious for their complexity in the preparation and instability of work. One of the problems is that if the generator is too far ahead of the discriminator in the pace of learning, then its selection of images is narrowed down to specifically those that help it to deceive the discriminator. In fact, as a result, generator training comes down to the creation of a single universal image to deceive the discriminator. This problem is called “collapse mode”.

GAN collapse mode is similar to Goodfellow's. Note that many of these bedroom images look very similar to each other. A source
Another problem is that when the generator effectively deceives the discriminator D ( g ( z ) ) , it operates with a very small gradient, therefore mathcalL textGANG( vecz) can not get enough data to find the true answer, in which this image would look more realistic.
The efforts of researchers to solve these problems were mainly aimed at changing the structure of the loss function. One of the simple changes proposed by Xudong Mao et al., 2016 , is to replace the loss function mathcalL textGAN for a couple of simple functions V textLSGAN which are based on smaller squares. This leads to a stabilization of the training process, obtaining higher-quality images and a lower chance of collapse using continuous gradients.
Another problem faced by researchers is the difficulty of obtaining high-resolution images, partly because the more detailed image gives the discriminator more information for detecting fake images. Modern GANs begin to train the network with low-resolution images and gradually add more and more layers until the desired image size is reached.

Gradually adding higher resolution layers during GAN training significantly improves the stability of the entire process, as well as the speed and quality of the resulting image.
Image-to-image broadcast
So far we have been talking about how to generate images from random sets of input data. But SPADE doesn't just use random data. This network uses an image called a segmentation map: it assigns each pixel a class of material (for example, grass, wood, water, stone, sky). From this map image, SPADE generates what looks like a photo. This is called the "Image-to-image broadcast".

Six different types of Image-to-image broadcasting, demonstrated by the pix2pix network. Pix2pix is the forerunner of two networks, which we will examine further: pix2pixHD and SPADE.
In order for the generator to learn this approach, it needs a set of segmentation maps and corresponding photos. We modify the GAN architecture so that both the generator and the discriminator receive a segmentation map. The generator, of course, needs a map in order to know which way to draw. It is also necessary for the discriminator to make sure that the generator places the right things in the right places.
During training, the generator learns not to plant grass where the sky is indicated on the segmentation map, because otherwise the discriminator will easily identify the fake image, and so on.

For image-to-image translation, the input image is received by both the generator and the discriminator. The discriminator additionally receives either the generator output data or the true output from the training data set. Example
Development of image-to-image translator
Let's look at the real image-to-image translator: pix2pixHD . By the way, SPADE is designed mostly in the image and likeness of pix2pixHD.
For the image-to-image translator, our generator creates an image and takes it as an input. We could just use a map of convolutional layers, but since convolutional layers only combine values in small areas, we need too many layers to transmit image information in high resolution.
pix2pixHD solves this problem more efficiently with the help of the “Encoder”, which reduces the scale of the input image, followed by the “Decoder”, which increases the scale to obtain the output image. As we will soon see, SPADE has a more elegant solution that does not require an encoder.

The pix2pixHD network scheme is at the “high” level. “Residual” blocks and “+ operation” refer to the “skip connections” technology of the Residual neural network . There are skip blocks in the network that correspond to each other in the encoder and decoder.
Batch normalization is a problem.
Almost all modern convolutional neural networks use packet normalization or one of its analogues to speed up and stabilize the training process. Activating each channel shifts the mean to 0 and the standard deviation to 1 before the pair of channel parameters beta and gamma allow them to denormalize again.
y= fracx− mathrmE[x] sqrt mathrmVar[x]+ epsilon∗ gamma+ beta
Unfortunately, packet normalization damages the generators, making it difficult for the network to implement some types of image processing. Instead of normalizing a batch of images, pix2pixHD uses the normalization standard , which normalizes each image separately.
Learning pix2pixHD
Modern GANs, such as pix2pixHD and SPADE, measure the realism of their output images in a slightly different way than was described for the original design of generative-contention networks.
To solve the problem of generating high-resolution images, pix2pixHD uses three discriminators of the same structure, each of which receives an output image at a different scale (normal size, reduced by 2 times and reduced by 4 times).
To determine its loss function, pix2pixHD uses V textLSGAN and also includes another element designed to make the generator outputs more realistic (regardless of whether it helps to deceive the discriminator). This item m a t h c a l L t e x t F M is called “feature matching” - it causes the generator to make the distribution of layers when simulating discrimination the same between real data and generator outputs, minimizing L 1 D i s t a n c e between them.
So, optimization is as follows:
$$ display $$ \ begin {equation *} \ min_G \ bigg (\ lambda \ sum_ {k = 1,2,3} V_ \ text {LSGAN} (G, D_k) + \ big (\ max_ {D_1, D_2 , D_3} \ sum_ {k = 1,2,3} \ mathcal {L} _ \ text {FM} (G, D_k) \ big) \ bigg) \ end {equation *}, $$ display $$
where losses are summed by three discriminatory factors and coefficient l a m b d a = 10 which controls the priority of both elements.

pix2pixHD uses a segmentation map made up of a real bedroom (on the left in each example) to create a fake bedroom (on the right).
Although discriminators reduce the scale of the image until the entire image is disassembled, they stop at “spots” measuring 70 × 70 (at appropriate scales). Then they simply summarize all the values of these “spots” for the entire image.
And this approach works great because the function m a t h c a l L t e x t F M makes sure that the image looks realistic in high resolution, and V t e x t L S G A N only required for checking small parts. This approach also has additional advantages in the form of network acceleration, reducing the number of parameters used and the possibility of using it to generate images of any size.

pix2pixHD generates photorealistic images with appropriate grimaces from simple sketches of faces. Each example shows a real image from the CelebA dataset on the left, a sketch of this celebrity's facial expression in the form of a sketch and the image created from this data on the right.
What is wrong with pix2pixHD?
These results are incredible, but we can do better. It turns out that pix2pixHD loses a lot in one important aspect.
Consider what pix2pixHD does with single-entry, for example, with a map that has grass everywhere. Since the entrance is spatially uniform, the outputs of the first convolutional layer are also the same. Then normalization of instances “normalizes” all (identical) values for each channel in the image and returns 0 as a conclusion for all of them. The β-parameter can shift this value from zero, but the fact remains: the output will no longer depend on whether the input is “grass”, “sky”, “water” or something else.

In pix2pixHD, instance normalization tends to ignore information from the segmentation map. For images consisting of one class, the network generates the same image independently of this class itself.
And the solution to this problem is the main feature of the SPADE design.
Solution: SPADE
Finally, we have reached a fundamentally new level in the creation of images from segmentation maps: spatial-adaptive (de) normalization (SPADE).
The idea behind SPADE is to prevent the semantic information from being lost in the network, allowing the segmentation map to control the normalization parameters γ, as well as β, locally, at the level of each individual layer. Instead of using only one pair of parameters for each channel, they are calculated for each spatial point by submitting a downsampled segmentation map through 2 convolutional layers.

Instead of rolling the segmentation map onto the first layer, SPADE uses its downsampled versions to modulate the normalized output for each layer.
The SPADE generator integrates the entire structure into small “residual blocks” that fit between the upsampling layers (transposed convolution):

SPADE high-level generator circuit versus pix2pixHD
Now that the segmentation map is being fed from the inside of the network, there is no need to use it as input for the first layer. Instead, we can return to the original GAN scheme, which used a random vector as input. This gives us an additional opportunity to generate different images from one segmentation map (“multimodal synthesis”). It also makes unnecessary the entire pix2pixHD “encoder”, and this is a serious simplification.
SPADE uses the same loss function as pix2pixHD, but with one change: instead of squaring the values V t e x t L S G A N it uses hinge loss .
With these changes we get great results:

Here the results of SPADE are compared with the results of pix2pixHD
Intuition
Let's think about how SPADE can show such results. In the example below, we have a tree. GauGAN uses one "tree" class to represent both the trunk and the leaves of the tree. However, somehow SPADE finds out that the narrow part at the bottom of the “tree” is the trunk and should be brown, while the large drop from above should be foliage.
The down-sampled segmentation that SPADE uses to modulate each layer provides similar “intuitive” recognition.
You may notice that the tree trunk continues in the part of the crown, which refers to the "foliage". So how does SPADE understand where to place part of the trunk there, and where is the foliage? After all, judging by the 5x5 map, there should be just a “tree” there.
The answer is that the area shown can receive information from lower resolution layers, where a 5x5 block contains the entire tree. Each subsequent convolutional layer also provides some movement of information in the image, which gives a more complete picture.
SPADE allows the segmentation map to directly modulate each layer, but this does not hinder the process of connected information distribution between layers, as it happens, for example, in pix2pixHD. This prevents the loss of semantic information, since it is updated in each subsequent layer at the expense of the previous one.
Transmission style
In SPADE, there is another magical solution - the ability to generate an image in a given style (for example, lighting, weather, time of year).

SPADE can generate several different images on the basis of a single segmentation map, mimicking a given style.
It works like this: we skip the images through the encoder and train it to set the generator vectors Z which in turn will generate similar images. After the encoder has been trained, we replace the corresponding segmentation maps with arbitrary ones, and the SPADE generator creates images that correspond to the new maps, but in the style of the provided images based on previously received training.
Since the generator usually expects to receive a sample on the basis of a multidimensional normal distribution, in order to obtain realistic images, we must train the encoder to derive values with a similar distribution. In fact, this is the idea of variational auto-encoders , which is explained by Yoel Zeldes .
This is how SPADE / GaiGAN functions. I hope this article has satisfied your curiosity about how the new NVIDIA system works. You can contact me via Twitter @AdamDanielKin or by email adam@AdamDKing.com.
Source: https://habr.com/ru/post/447896/
All Articles