Universal method for solving problems on the example of the puzzle "12 coins, 3 weighings"
Given: 12 coins, one of them is fake, differs only in weight. Unknown lighter or harder. There are given lever scales that show that the load on one side is heavier. For 3 weighing you need to find a fake coin.
From experience, I advise you not to hurry, to decide in writing. The puzzle “12 coins, 3 weighings” appeared several times in my life. The first time I was asked by my fellow Olympiad, I decided it after the Olympiad, and I had a couple of hours to break my head. And after a few years it was not immediately given to me. If you want to decide for yourself - do it on a piece of paper.
Below will be an analysis and solution stages. The stages will be carried out according to a universal method of solving problems, which is applicable both to programming and to life. Thanks to the approach, solving the puzzle will be easy.
I suggest you before reading to suggest a solution. Do you have an answer? Tested?
')
If it were the software questions would be the following: “Have you programmed, tested the algorithm? Considered test cases and checked them? ".
Experience shows that to solve it is required to draw a decision tree and check all 12 cases.

From experience, I advise you not to hurry, to decide in writing. The puzzle “12 coins, 3 weighings” appeared several times in my life. The first time I was asked by my fellow Olympiad, I decided it after the Olympiad, and I had a couple of hours to break my head. And after a few years it was not immediately given to me. If you want to decide for yourself - do it on a piece of paper.
Below will be an analysis and solution stages. The stages will be carried out according to a universal method of solving problems, which is applicable both to programming and to life. Thanks to the approach, solving the puzzle will be easy.
I suggest you before reading to suggest a solution. Do you have an answer? Tested?
')
If it were the software questions would be the following: “Have you programmed, tested the algorithm? Considered test cases and checked them? ".
Experience shows that to solve it is required to draw a decision tree and check all 12 cases.

1. Tips
In the process of solving will help:
1) Reduction of entropy (measure of uncertainty) and answers to the questions:
Questions are suitable for any task projects. Answers to them help in reducing the risks of missed deadlines, overspending the budget and getting a ouster from the authorities.
2) Decomposition. Approach from simple to complex. If you prepare a solution to the simplest cases, then use them to solve the problem (divide and conquer algorithm), it will be easier than to imagine the whole situation in your head.
The divide-and-conquer algorithms divide a task into two or more subtasks of the same type, but smaller to elementary tasks, and combine their solutions to get an answer to the original problem.
Compose questions for decomposition. What would you suggest?
1) Reduction of entropy (measure of uncertainty) and answers to the questions:
- What did you learn in the previous step?
- What reduces uncertainty?
- What information do we have?
- What else do you need to know?
Questions are suitable for any task projects. Answers to them help in reducing the risks of missed deadlines, overspending the budget and getting a ouster from the authorities.
2) Decomposition. Approach from simple to complex. If you prepare a solution to the simplest cases, then use them to solve the problem (divide and conquer algorithm), it will be easier than to imagine the whole situation in your head.
The divide-and-conquer algorithms divide a task into two or more subtasks of the same type, but smaller to elementary tasks, and combine their solutions to get an answer to the original problem.
Compose questions for decomposition. What would you suggest?
2. Decomposition
What questions have you formulated for decomposition? Any coincidences?
1) What is the most elementary situation? What can we do in one weighing?
For one weighing we can determine which coin is heavier, whether the weight of the coins is equal.
2) If we have 2 coins, and, as we know, fake is heavier or lighter. How to determine a fake one weighing?
It is necessary to weigh the coins, and to determine the false one, depending on the arrow of the scale.
3) If we have 2 coins, and, it is not known, a fake is heavier or easier, how to determine a false one in one weighing?
After weighing one of the 2 presented coins with the third coin, about which it is known that it is genuine.
4) If we have 3 coins, and it is known that a fake is heavier or lighter. How to determine a fake one weighing?
It is necessary to compare any two of these coins, if they are equal, the third coin is a false one.
5) If we have 3 coins, and, unknown, a fake is heavier or lighter. Is it possible to determine a fake one weighing?
Unfortunately not.
6) If we have 4 coins, and is it unknown if a fake is heavier or lighter, can we identify a false one at the same time?
Unfortunately not.
7) If we have 4 coins, and, unknownly, a fake is heavier or lighter, for how many weighings can we determine a false one?
For two weighing.
Further from the elementary cases we will collect situations from 8, 9, 10, 11 and 12 coins. How do you see the solution?
Below is the complete solution.
1) What is the most elementary situation? What can we do in one weighing?
For one weighing we can determine which coin is heavier, whether the weight of the coins is equal.
2) If we have 2 coins, and, as we know, fake is heavier or lighter. How to determine a fake one weighing?
It is necessary to weigh the coins, and to determine the false one, depending on the arrow of the scale.
3) If we have 2 coins, and, it is not known, a fake is heavier or easier, how to determine a false one in one weighing?
After weighing one of the 2 presented coins with the third coin, about which it is known that it is genuine.
4) If we have 3 coins, and it is known that a fake is heavier or lighter. How to determine a fake one weighing?
It is necessary to compare any two of these coins, if they are equal, the third coin is a false one.
5) If we have 3 coins, and, unknown, a fake is heavier or lighter. Is it possible to determine a fake one weighing?
Unfortunately not.
6) If we have 4 coins, and is it unknown if a fake is heavier or lighter, can we identify a false one at the same time?
Unfortunately not.
7) If we have 4 coins, and, unknownly, a fake is heavier or lighter, for how many weighings can we determine a false one?
For two weighing.
Further from the elementary cases we will collect situations from 8, 9, 10, 11 and 12 coins. How do you see the solution?
Below is the complete solution.
3. Decision
The first step: divide the coins into 3 groups of 4: 1 2 3 4, 5 6 7 8, 9 10 11 12.
Compare the first two groups. There are three options:

1) If the groups are equal, then the counterfeit coin is in the third group. It is necessary to find a fake coin of 4 coins for two weighings.
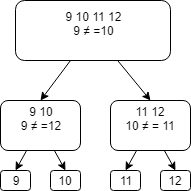
Divide the third group into two: 9 10 11 12
Compare 9 and 10:
So we found a fake coin.
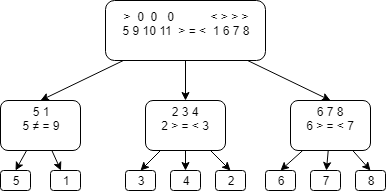
2) Consider the second case. If the first group is heavier than the second, then we assign the first character “>”, the second group “<”, the third group - “0”.

We divide the coins into groups of 1 9 10 11 and 5 2 3 4, we weigh. There are three options:
3) The case when the second group is heavier than the first is similar to the second.
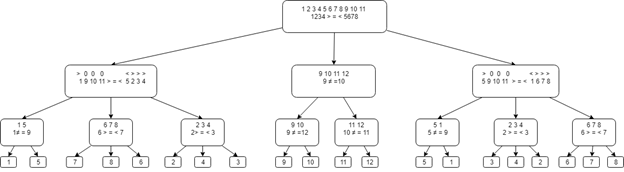
The general diagram of the “Decision Tree” is presented below.
Compare the first two groups. There are three options:
- the first group is heavier;
- the second group is heavier;
- are equal.

1) If the groups are equal, then the counterfeit coin is in the third group. It is necessary to find a fake coin of 4 coins for two weighings.

Divide the third group into two: 9 10 11 12
Compare 9 and 10:
- if they are equal, then a fake coin in the second group - we compare 9 and 11. If 9 and 11 are equal, then a false one - 12, if not -11
- if they are not equal, then fake in the first group - we compare 10 and 12. If 10 and 12 are equal - fake - 9, if not - 10.
So we found a fake coin.
2) Consider the second case. If the first group is heavier than the second, then we assign the first character “>”, the second group “<”, the third group - “0”.

We divide the coins into groups of 1 9 10 11 and 5 2 3 4, we weigh. There are three options:
- Are equal. A fake coin is among the numbers: 6 7 8. Compare 6 and 7, if equal - fake - 8, if 6 is more, then fake - 7, if 7 is more, then fake - 6, since in this case the fake coin is easier.
- The first group is heavier, then a fake coin is either 1 or 5. We compare 1 and 9, if they are equal - a fake coin - 5, if not - 1.
- The first group is easier, then fake among 2 3 4 coins, since it is known that 9, 10 and 11 are real, and the second group can only outweigh coins 2, 3 and 4. We compare 2 and 3, if equal, fake 4, if 2 is heavier, then false is 2, otherwise the 3rd is fake.
3) The case when the second group is heavier than the first is similar to the second.

The general diagram of the “Decision Tree” is presented below.

Conclusion
Upon receipt of the task for revision or debugging, it is good to apply the approach discussed above:
Successful decisions.
- Decide what is given?
- Which elementary cases / tasks can be decomposed?
- What is unknown to solve the problem? What experiments need to be carried out to reduce the entropy?
- Run.
- Problem solved? Not? Return to step 1.
Successful decisions.
Source: https://habr.com/ru/post/447354/
All Articles