Pyramids not on Mars: exploring the shape of nanocrystalline clusters under a graphene layer

Very many properties, and therefore methods of applying something, depend on the shape of this object. Everything is very simple and as much logical: round wheels will roll better than square wheels, and the wings of the aircraft have a certain shape that improves aerodynamics. Even ordinary pencils have the shape of a hexagon, so that it is more convenient to hold in your hand when writing and not to look for it throughout the apartment under all the sofas and cabinets in the pose of the person who first launched Dark Souls. A change in form can lead to a change in properties, and if these changes are controlled, then you can get certain properties you need. This is exactly what the scientists in the study we are considering today did. They created a “constant elasticity” model for copper nanocrystalline clusters under a graphene membrane. How and why did scientists “plaster” copper with graphene, what results did practical experiments show, do they agree with preliminary calculations and what does this “sandwich” on a nanometer scale mean for science? Answers to these questions await us in the report of the research group. Go.

The basis of the study

As the scientists themselves say, there is nothing more important than the structure and form of functional crystals (scientists have their own life priorities, we will not quibble). During the synthesis of these small objects, some deviations from the equilibrium structure are possible, which can be either a very unpleasant minus or a big plus. If you understand the very essence of the equilibrium structure, you can learn to better understand these structures, and as a consequence, and manipulate them.
')
An important role in this is played by nanocrystals (NC), which are divided into several classes: unsupported three-dimensional NC, obtained by liquid-phase synthesis, and supported three-and two-dimensional NC, obtained by deposition on the surface of the substrate.

If we connect our favorite word “quantum” to all of this, we will know the following: for quantum dots, i.e. supported three-dimensional NK, formed by the lattice mismatch within heteroepitaxy * , the deformation plays an important role in controlling the shape.

Heteroepitaxy * is a type of epitaxy (growth of one crystalline material on top of another at low temperatures), when the growing layer differs from the substrate in chemical composition.

In this study, scientists are considering a new type of three-dimensional nanocrystals (clusters), which are located under the layered material. Thus, these NCs are compressed under one or several monolayers (above) and a set of semi-infinite layers (below).

Why do scientists do this, you ask. They will answer: the purpose of this study is to develop and analyze a model of constant elasticity (PE), which combines the deformation energy of the upper graphene layer, adhesion and surface energy of Cu (copper), graphene and graphite, which allows you to control the equilibrium shape of the surface / encapsulated clusters .

Scientists managed to create such a model, after which they tested its viability not on paper, but in reality. What results the analysis showed, and what discrepancies were observed between theory and practice, we consider further.

Preparation for the study

At the very beginning it was necessary to prepare graphite for interaction with copper nanoclusters. To this end, defects were created on its surface using Ar + bombardment. After that, Cu atoms collided with the surface of graphite, penetrating through some defects and were already under the surface of graphite. During this action, the graphite substrate is heated to 600–800 K. Such a temperature mode is chosen for a reason: Cu islands (clusters) on the surface of graphite begin to coarse at 550–600 K, therefore, the Cu – Cu bond should be easily broken at 600 K and above. As a result, islands of copper were formed in this study at a temperature of 800 K.


Image number 1

In the snapshot of STM 1a, we see not pyramids on the surface of the red planet, but those very islands of copper, whose STM profile is shown in 1a ' .

Scientists direct our attention to the shape of this copper island: a hexagon with a flat top. The flattening of the apex and, accordingly, the bottom indicates the limitedness of the central part of the island by the substrate layer (bottom) and the graphene layer (top). We also see slopes forming a ring around a flat top. According to observations, the thickness of the carbon layer on these islands can be several monolayers of graphene, up to three.

Next, scientists analyzed the shape of the island ( 1b ). It became clear that height (h) scales almost identically with the ring width (a). At the same time, the slopes (h / a), that is, the slope of the sides, are constant for different sizes. But the diameter, unlike the width of the ring, scales poorly with height, that is, the aspect ratio d / h is not constant. Graph 1c shows the ratio of the height and width of the ring, and Graph 1d shows the height and width of the top of the island. In this case, a total of about 140 copper islands were analyzed.

How real things are with copper nano-formations under the graphene layer is now clear to us. After these observations, the scientists proceeded to create their model of constant elasticity (PE).

PE model

In the process of modeling, the scientists decided to apply an approximation (approximation) of the shape of the island of copper, therefore not a hexagonal pyramid was used, but a cylindrical one. A copper cylinder grows between a single / multiple monolayer graphene membrane and a graphite substrate.

It is assumed that the graphite substrate is rigid, and the covering layer (above the copper islands) is subjected to elastic deformations of stretching and bending, which allows it to fit under the growing island.

A small clarification of terms: later in their work, scientists call the islands a set of a Cu cluster, a deformed graphene membrane and a graphite substrate, and clusters only the central metal part.

An important element of the shape of the islands are the slopes of the sides. These slopes are significantly smaller than those of the low-index (111) or (100) Cu planes, which naturally adjoin the upper face (111) for the supported Cu cluster. From this it follows that the annular space filled with copper is not an energetically viable configuration due to the high index surface and the Cu surface energy.

The next important feature is the presence of folds of the ring, one of which can be seen in the lower left corner at 1a. Such deformations suggest that the membrane (covering layer) is not influenced by the stretching of the underlying material, which limits its folding.

The system energy (Π) can be modeled as the sum of the elastic deformation energies of a distorted graphene film (U _e ) and a set of variables representing the interface and surface components of the system. Interfaces and surfaces include: pure copper, graphene – graphite (GnGt), copper – graphene, and copper – graphite (the designation for both is CuG). The above are the following IS energy:

• energy costs associated with the surface energy of Cu, U _Cu and loss of adhesion Gn - Gt, U _GnGt ;
• energy reduction due to adhesion of Cu - Gn and Cu - Gt, U _GnGt .

Together, they will be referred to as the general term - U _IS . Below is the formula for total energy:

Π = U _Cu + U _GnGt + U _CuG + U _e

The equilibrium form was obtained by minimizing Π for a fixed volume (V) of the Cu cluster.

Then U _IS were calculated, that is, the interface and surface components of the total energy of the system. Each such component can be expressed as the sum of the products of surface energy (γ) or adhesion energy (β) multiplied by the corresponding area.


Table 1: formulas for calculating U _IS (left) and input data (right).

The values ​​of γ and β were obtained by means of the density functional theory. A (111) orientation of the Cu cluster was obtained from experimental data.

Next, the scientists derived the U _e value by means of the calculated model SLBT (blister test with a cylindrical rod with a flat top), in which the cylindrical rod moves upwards through a hole in a solid surface, clinging to an elastic membrane and deforming it.

The membrane undergoes stretching and bending deformations. In the SLBT model, these two types of deformations are approximated as independent contributions. The calculations showed that the flexion deformation is rather small taking into account the size of the experimental structure; therefore, modeling the total elastic energy of the membrane (U _e ) was possible only with allowance for tensile deformation.

The annular space can react to the growth of the island without restrictions, however, the adhesion between the part of graphene on the top of the island and copper can prevent lateral stretching of the graphene. If the stretching flows freely, then this part can also freely deform over the top of the island.

Given this statement, the formula U _e was derived (No. 5 in table 1). From it we can understand that the value of U _e depends on the Poisson's ratio (v), the modulus of longitudinal elasticity (Y), and the thickness of graphene (t). The value of v was 0.165, Y - 1.1 TPa, since this corresponds to the experimental values ​​of the density of defects (7.3 ± 0.4) x10 ³ μm ^-2 .

Regarding the thickness of graphene, we already know that graphene over the islands may be more than one monolayer thick. This allows us to calculate the thickness of the upper layer of the structure under study using the formula t = L · t _GML , where L is the number of graphene layers and t _GML is 0.34 nm (the interlayer distance in crystalline graphite).

Research results

So. With the observational data sorted out, with the calculation part, too, it's time to start the results of the analysis of all this in the aggregate.

Considering the formulas U _IS and U _e , as well as the data from table 1 (on the right), Π becomes a function of only three independent parameters - a, h, and d. This problem can be solved by precisely determining the value of the cluster volume V = πhd 2/4, which allows eliminating either h or d. Thus, only two parameters will be obtained, not three: Π = Π (a, h) or Π = (a, d). For the demonstration, the scientists used Π (a, h), and the cluster volume was taken from the data used - 〈V _exp = 4x10 ⁴ nm ³ (image No. 2).


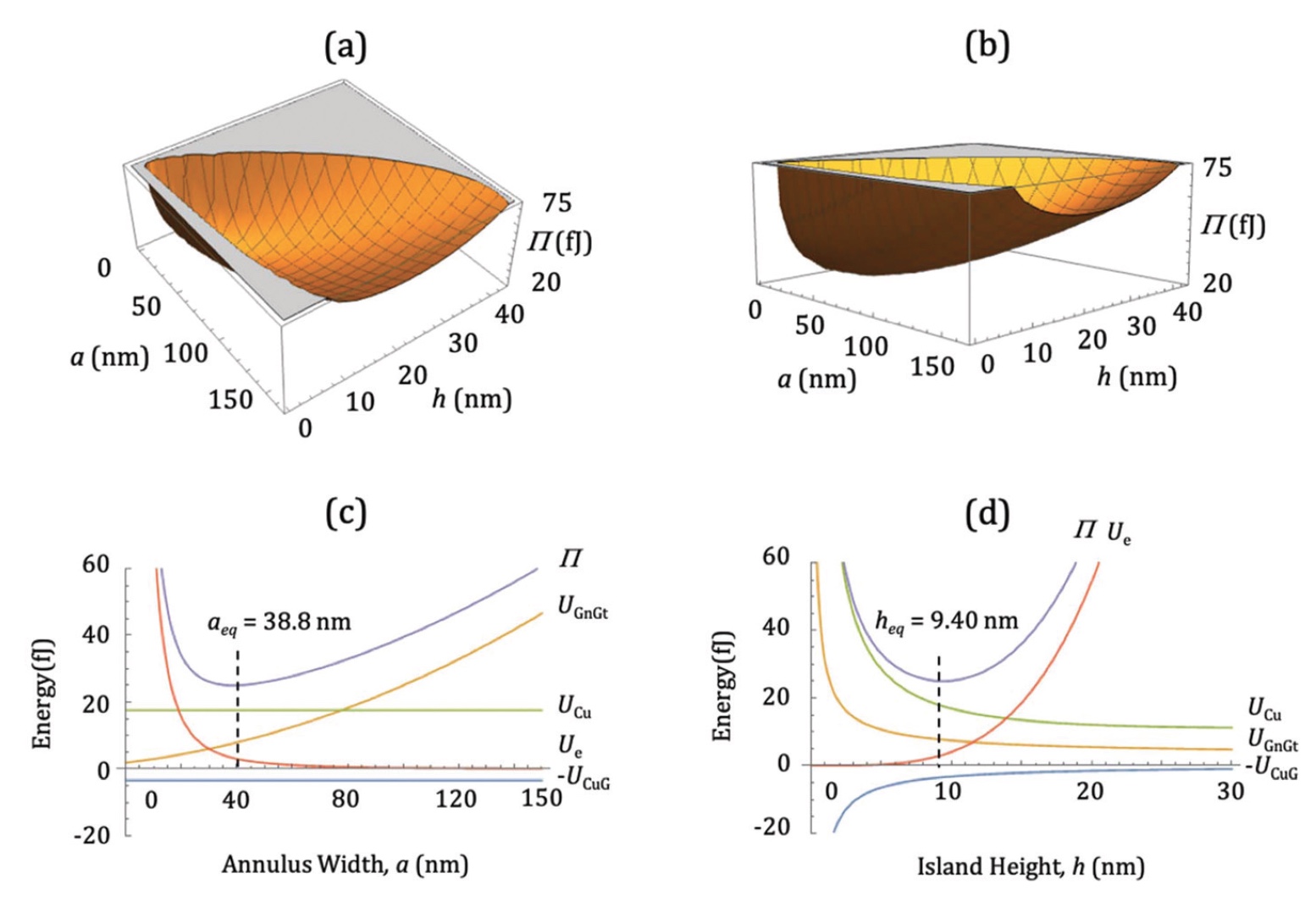
Image number 2

Scientists point out an extremely important point: there is a certain minimum value of Π, which is a state of equilibrium. With such a minimum, the model of constant elasticity predicts the following values: a _eq = 38.8 nm, h _eq = 9.4 nm, and d _eq = 73.6 nm. In the experiments, the islands that were close in terms of 〈V _exp 〉 had the following parameters: 〈a _exp = 31 ± 11 nm, _{〈h exp〉} = 7.3 ± 2.6 nm and 〈d _exp = 88 ± 21 nm. As we can see, the theoretical and practical data are in very good agreement.

Plots 2c and 2d show two orthogonal cuts through Π (a, h), each of which passes through a global minimum.

The above processes can be repeated in the whole range of experimentally observed cluster volumes (1.8x10 ³ nm ³ ≤ V ≤ 6.9x10 ⁵ nm ³ ). Therefore, it is possible to compare the size of islands predicted by the model and observed in experiments. For a simpler comparison of the model and experiment, the ratio of the sizes of the islands and the value of h is used (image No. 3).


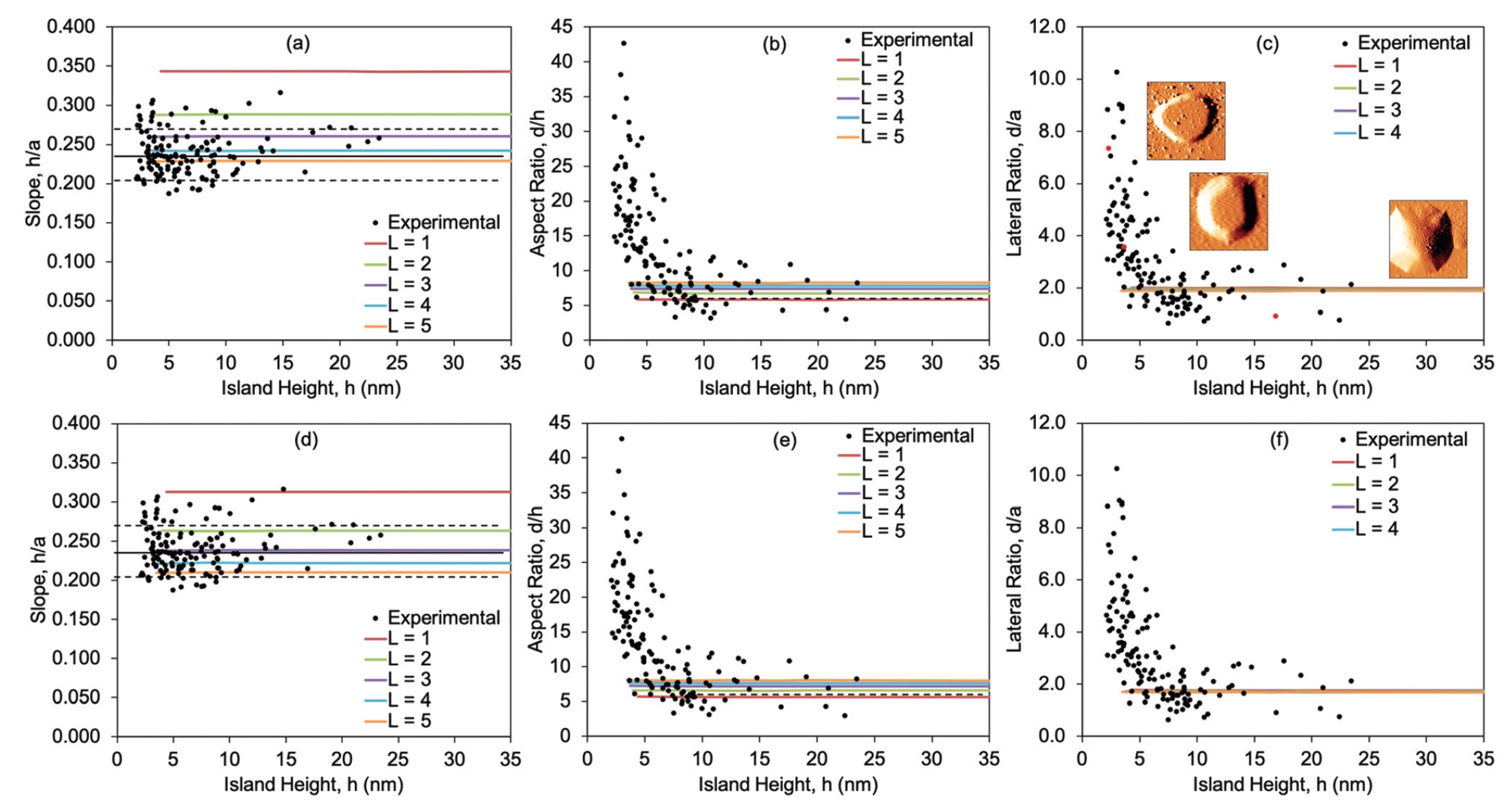
Image number 3

The graphs above show the h / a, d / h and d / a values ​​for both the model and the experiment. Plots 3a - 3c are a comparison of experimental data and a SLBT model, in which membrane expansion proceeds without restrictions, and 3d - 3f is already experimental data and a model with limited expansion.

The h / a value in the experiments is constant and equals 0.24 ± 0.03 over the entire range of island sizes. In theory, the volume of clusters 1 ≤ L ≤ 5 was used, and the best agreement between the indicators of theory and practice was found at L = 4.

There are unusual changes in the d / h value (and parallel to d / a). As can be seen from graph 3b, the experimental d / h value starts at 40, but then begins to decrease sharply with increasing h value. When h reaches ≈ 10 nm, the d / h value is aligned to 7.3 ± 2.8 (horizontal dashed line at 3b). The theoretical model showed d / h values ​​in the range from 5.6 to 8.0 for L = 1 ... 5.

With a fixed SLBT model, the figures are very similar to the free SLBT model. The only significant difference is that for some value of L, the ratio h / a in the fixed model is slightly less than in the free model. Thus, the best agreement between theory and practice in the case of a fixed SLBT model is manifested at L = 3.

For more detailed acquaintance with the study I strongly recommend to look into the report of the research group .

Epilogue

What do we have in aggregate? Scientists have created a theoretical model that is in excellent agreement with experimental data. This model demonstrates that the shape of nanocrystalline copper clusters is preserved, at least in the case of scales, when the bending strain is not very strong. The researchers also found that delamination in the annular space is a reaction to the displacement of the membrane (covering layer) upwards exclusively in the central region (inner circumference of the ring) and reflects the properties of graphene / graphite, and not copper itself.

In addition, it was found that similar observations described above are real for systems in which a metal cluster is embedded near the surface of a layered three-dimensional material or under a supported two-dimensional membrane, but only under the condition of an equilibrium shape. In this case, it is necessary (and perhaps, as the results showed) to use the mechanical properties of the membrane, adhesion and surface energies to predict the equilibrium shape of the encapsulated body, that is, metal clusters (in this copper work). This principle works in the opposite direction - one can learn the energy and mechanical properties by measuring the size of clusters. Scientists give a short example: by measuring h and a and knowing the mechanical properties of the membrane, one can determine the adhesion energy of the membrane-substrate.

In the best way this work can be used in modern technologies that rely on layered materials - graphite or its derivatives, like graphene. And if we consider that the tendency to reduce the physical size of electronic devices is not yet declining, then such studies have a high price, and therefore we will wait for new shocking discoveries and amazing experiments.

Thank you for your attention, stay curious and have a good working week, guys!

Thank you for staying with us. Do you like our articles? Want to see more interesting materials? Support us by placing an order or recommending to friends, 30% discount for Habr's users on a unique analogue of the entry-level servers that we invented for you: The whole truth about VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps from $ 20 or how to share the server? (Options are available with RAID1 and RAID10, up to 24 cores and up to 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps before summer for free if you pay for a period of six months, you can order here .

Dell R730xd 2 times cheaper? Only we have 2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV from $ 249 in the Netherlands and the USA! Read about How to build an infrastructure building. class c using servers Dell R730xd E5-2650 v4 worth 9000 euros for a penny?