Fractals in irrational numbers. Part 2
Part 0: Fractals in prime numbers.
Part 1: Fractals in irrational numbers.

The article contains Gif and contrasting pictures. Epileptic seizures may occur.
In the previous article, we looked at the binary sequence visualization algorithm. Let's remember.
')
Take the binary sequence. As an example, the first few bits of the fractal sequence discussed in the previous article:
0100110110010011001001101100
Draw a square cell field. Set the bits at the upper border. The distance between the bits is two cells:

For each bit, draw a diagonal dotted trajectory (through the cell). For zeros, draw the first stroke to the right:
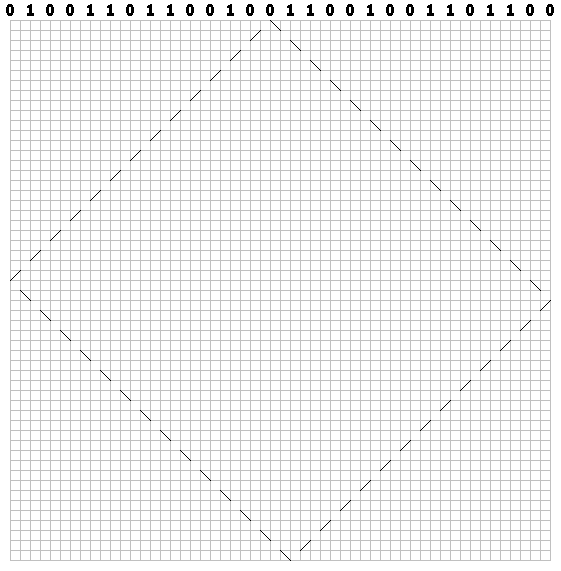
For units, left:
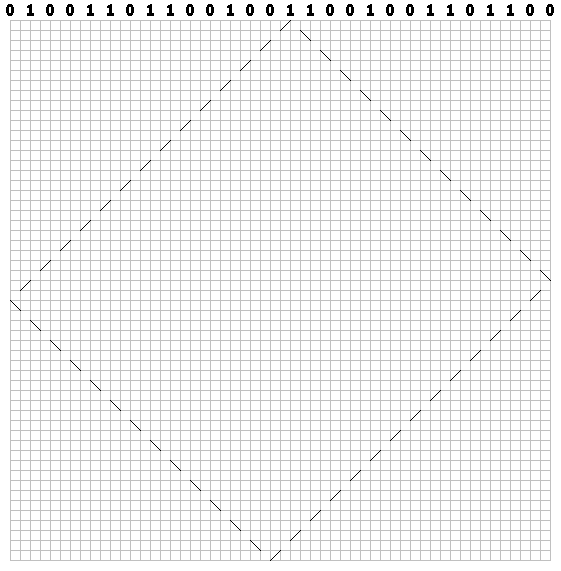
Draw a trajectory for each bit. Got a "billiard" pattern:

Identical pattern (without a defect along the diagonal - the sequence is infinite, we visualized it as a final sequence) can be obtained in another way. We invert every even bit in the sequence:
0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 1 1 1 1
Next, for each bit, draw vertical dashed lines:

Place bits on the left, draw horizontal lines:

Combine:

After writing the first article, two questions remained unresolved:
1. Is it possible to draw a fractal pattern for irrational numbers? Can. The question was solved in the previous article. The picture above is part of the fractal pattern for . If you select one of the curves on this pattern:

We get the well-known fractal curve - “Fibonacci word fractal”.
2. The second question is whether it is possible to write an algorithm that paints a pattern:

We will deal with the second question in this article. We will color the patterns using a weaving machine, which we will simulate using JavaScript.

In the diagram above - the easiest machine. It consists of two frames through which the threads are stretched. The frames are connected to the pedals. When you press one of the pedals, one of the frames rises. The threads stretched through this frame are raised and a transverse thread is pulled into the resulting gap between the threads. If even and odd threads are pulled through different frames, weaving is obtained in a checkerboard pattern:

In more complex machines, four or more frames are used:

Ashford 4 Shaft Table Loom
In order not to get confused about which pedal to press - they make a scheme.
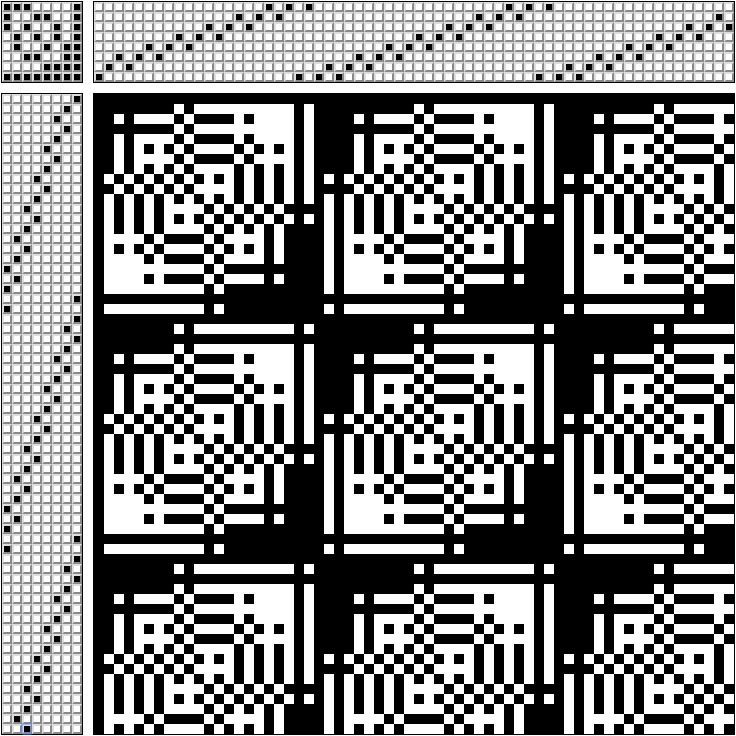
In the upper right part of the scheme, it is noted which frames the threads pass (the scheme for a loom for 8 frames).
In the upper left corner - which pedals to clamp at the same time (each pedal is connected only with its own frame).
In the left bottom part - in what order to clamp the pedals.
In the lower right - what kind of interweaving we get. If we stretch the white thread through the black we get a monochrome pattern.
Immediately "move" in principle may seem a bit difficult. The picture below shows how the weaving pattern is formed:

Let's write a script. Pull the thread through the frame will be using a one-dimensional array array2. In the one-dimensional array array1 we write the sequence of pedaling. In array3 (8x8 binary array), write down which pedals to clamp at the same time.

Script (works in Google Chrome).
With the help of our improvised loom, we can draw a wide variety of patterns:

But historically, the average person has no more than two legs. Therefore, it is convenient to simultaneously clamp no more than two pedals. One of the most popular patterns for a loom is as follows:
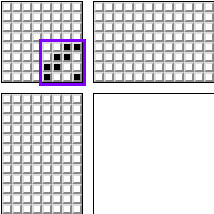
For 4 frames. And its modification for 8 frames:

Suddenly, patterns (or a fragment of patterns) made using this pattern are similar to our "billiard" patterns. In addition, these patterns are shaded:

You can learn how to select "billiard" patterns for the loom. Example:

At the beginning of the article we have already seen a fragment of this pattern.
Finish with looms and write a script to visualize the binary sequences. We can get rid of one of the arrays - the pattern is symmetrical diagonally. How to fill the remaining array? Elementary:

Take the sequence for . Create an array. In the zero element of the array write the zero bit of the sequence. Alternately take every bit of the sequence. If the n-th bit = 1 - write to the array a [n] = a [n-1] +1. If bit = 0, write a [n] = a [n-1] -1
Checking:

In fact, we have already received an elementary fractal, but we will continue.
Next, let's deal with the matrix:

Summarize and . We divide by the module by 4. If the resulting result is = 0 or 1, we write to the matrix true. For 2 and 3, write false. We can do without the matrix (it is not known in advance what the maximum and minimum values are taken by a [n]). Sum the a [x] and a [y]. We add some number to the resulting amount. (to get rid of those cases when the sum is a negative number). Divide modulo 4. For values 0 and 1, paint over a pixel with coordinates and .
The final algorithm takes only a few lines:
Visualize our fractal sequences.

You can easily modify the script in order to get an RGB image:

Above, we added a certain number to the sum of a [x] + a [y] . If you do not add this number - the minimum value of the sum = -8, maximum = 8 (for and from 0 to 750). If you remove - in some cases, the sum is negative and not a multiple of 4, and for these cases the pixel is not painted (remains black):

It can be imagined as if a part of the fractal is below some imaginary border (below this border only negative values are multiplied by multiples of 4: -4, -8, -12, ...).
We can see where this border is:

Instead of dividing by module, we can compare the sum with a certain specific value and thus paint over only one “layer” of the fractal. As an example, take the average between the minimum and maximum values:

By changing the values from minimum to maximum, we can see how the “layers” change over time:

In addition, we can “head on” compare a [x] with a [y] and also get a fractal pattern:

The following sequence:
Fractal:

RGB:

Middle layer:

In dynamics:

Fractal:

RGB:

Middle layer:

In dynamics:

Fractal:

RGB:

Middle layer:

In dynamics:
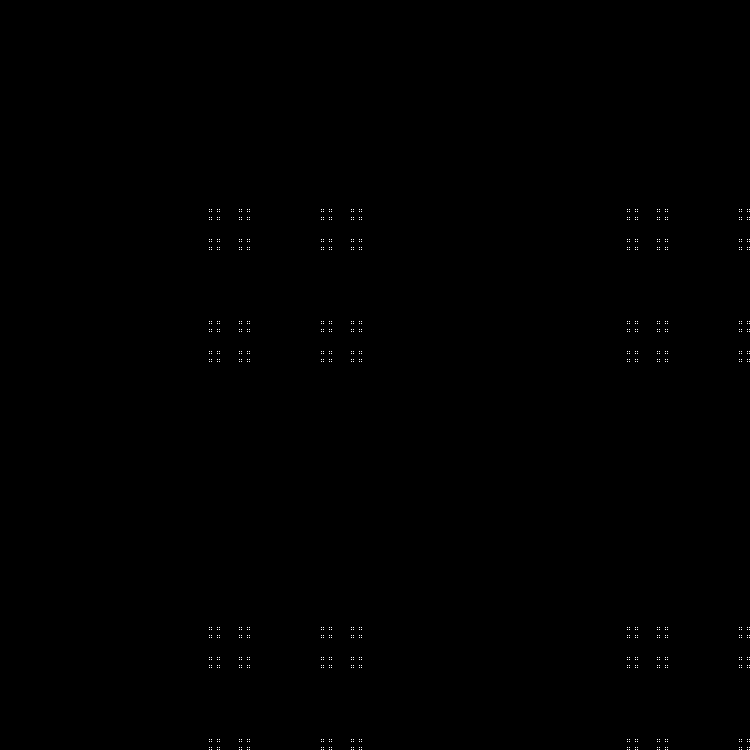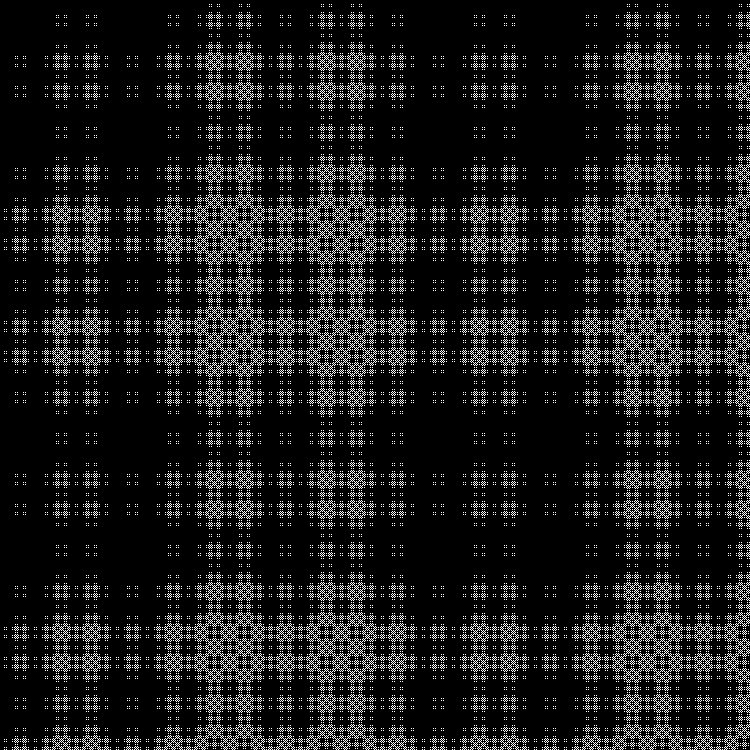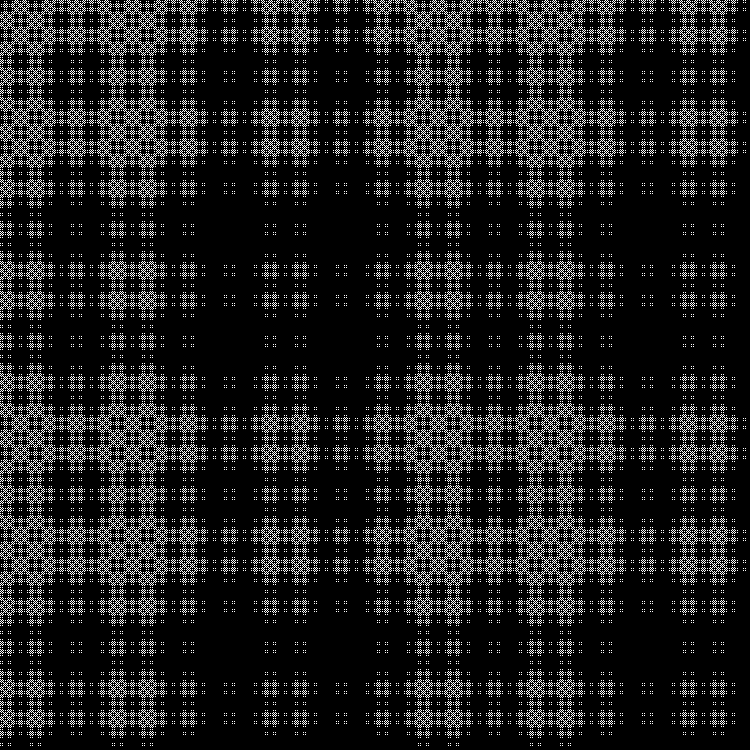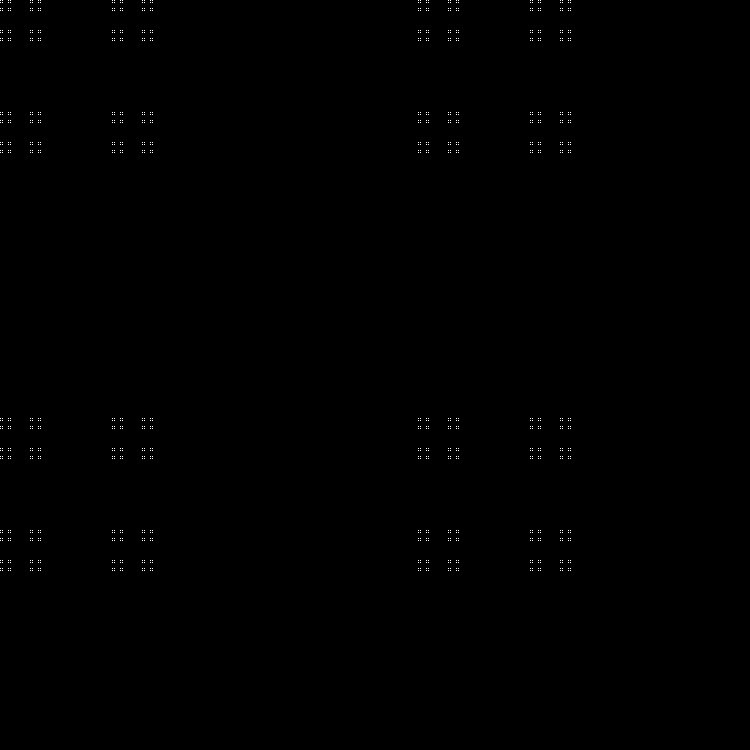
Fractal:

RGB:

Middle layer:

In dynamics:

Well, our favorite fractal (part of this pattern can be drawn using billiards, with the sides equal to Fibonacci numbers):
Fractal:

RGB:

Middle layer:

In dynamics:
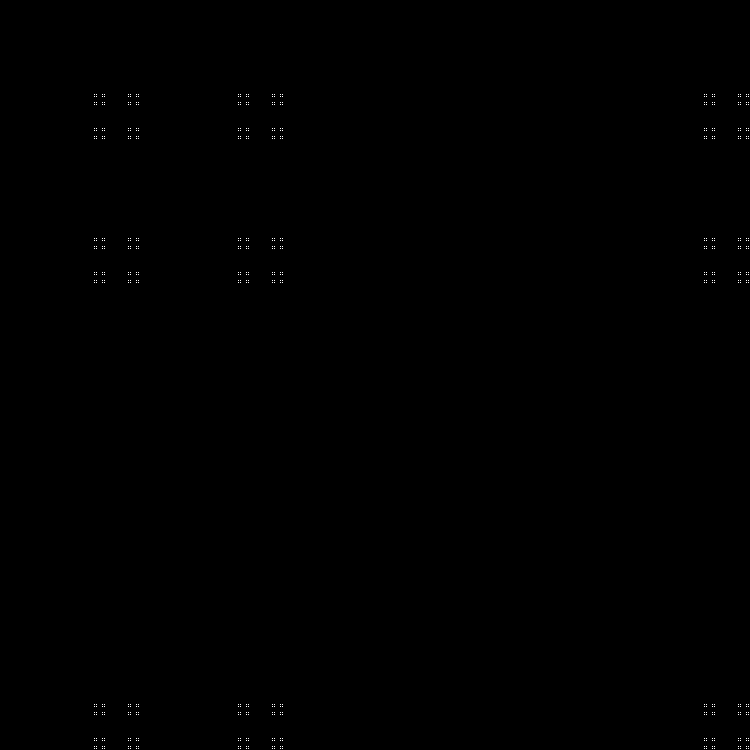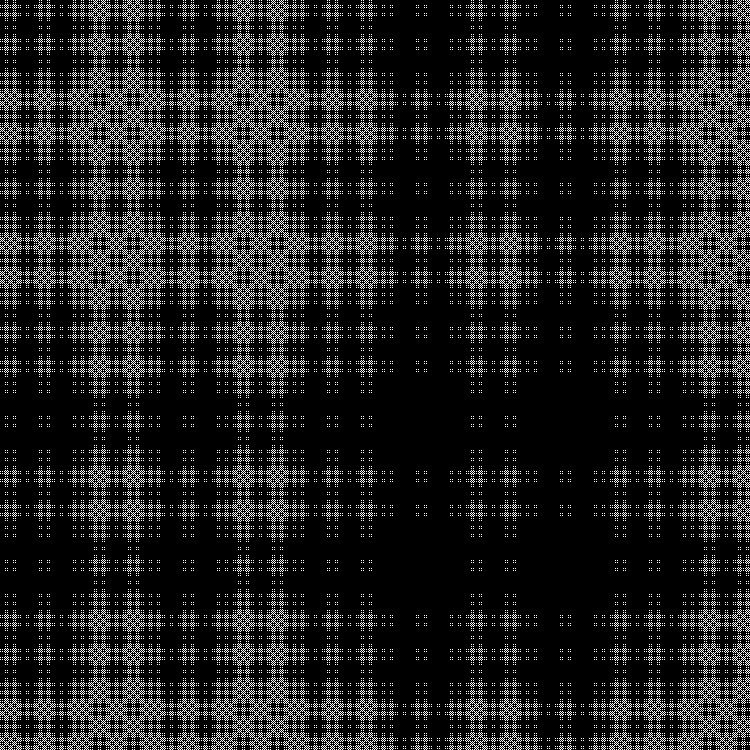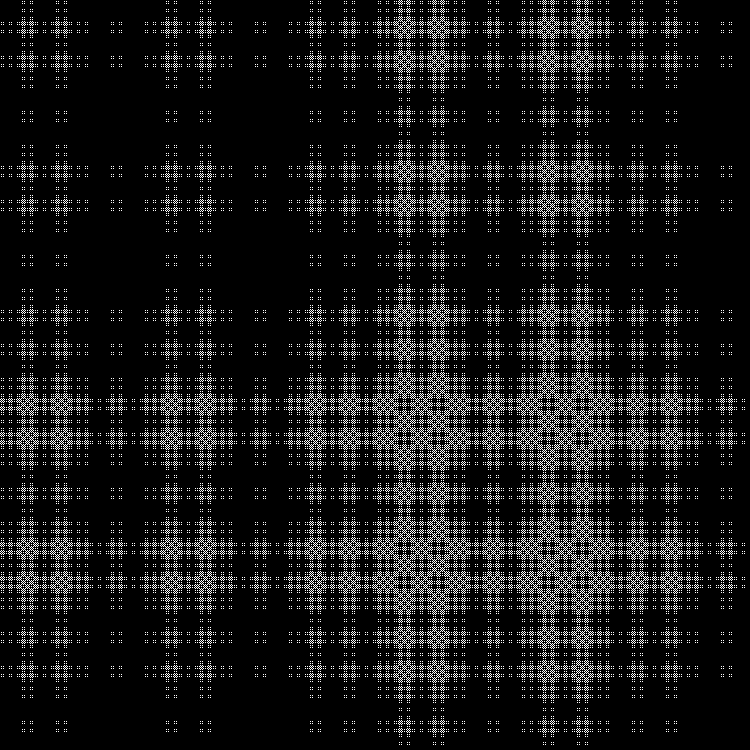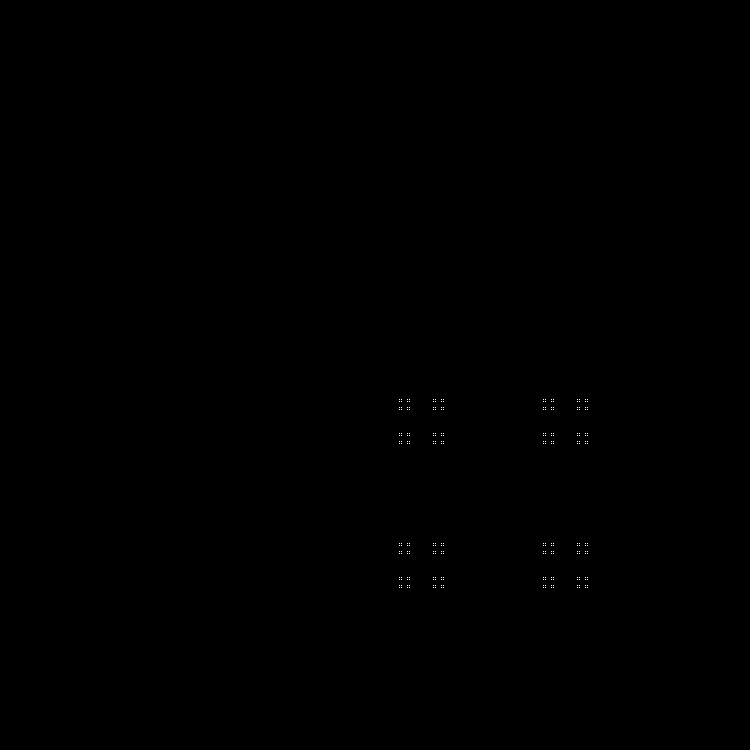
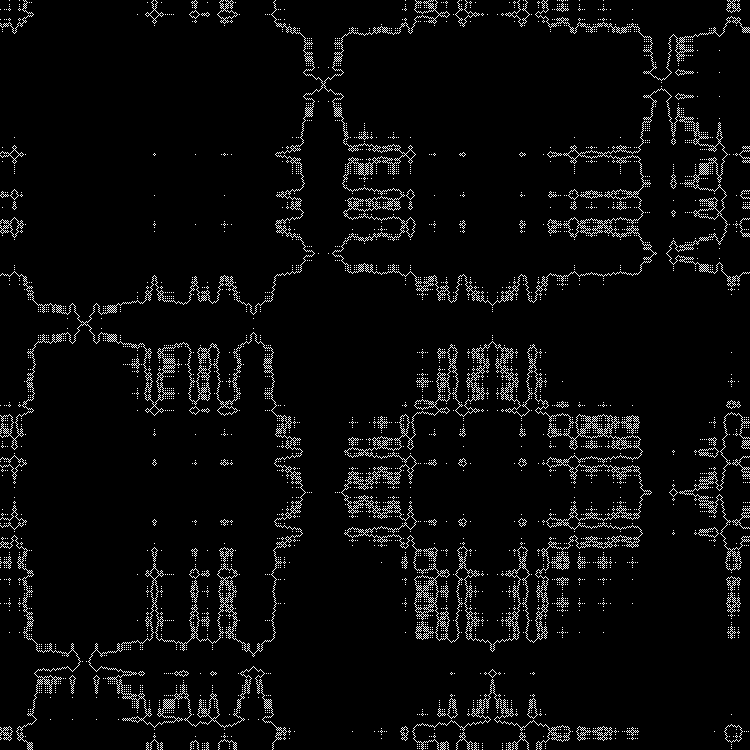
Another sequence to complete:
Pattern:

RGB:

Middle layer:
In dynamics:
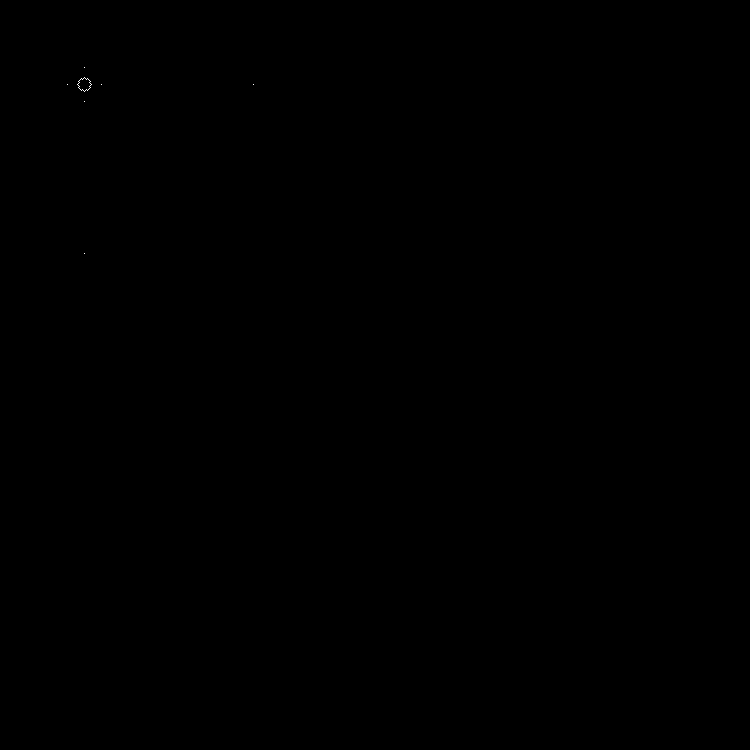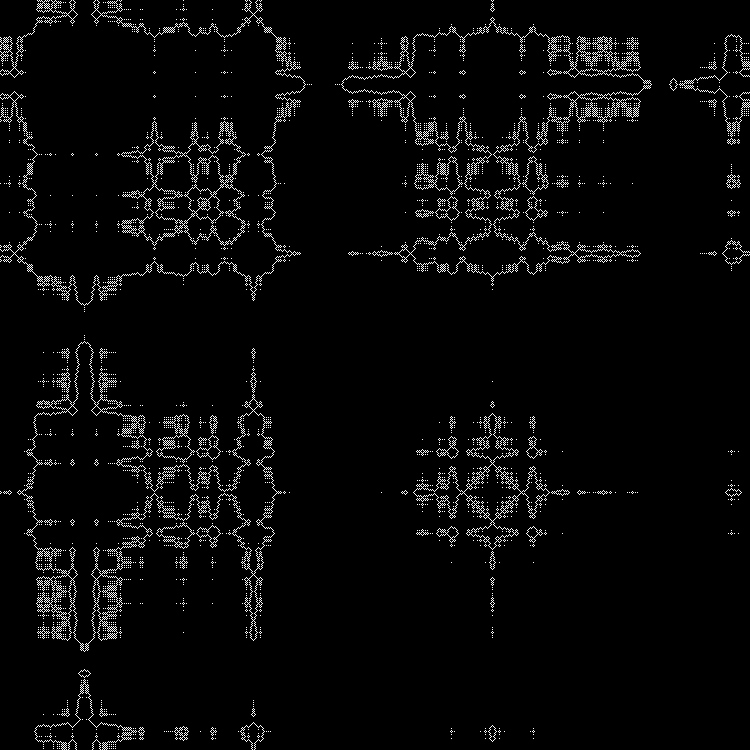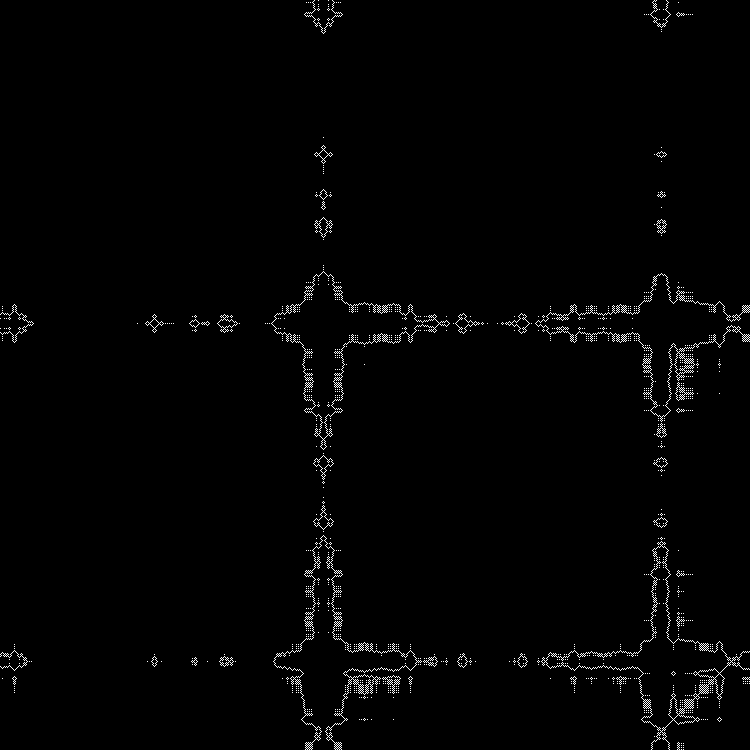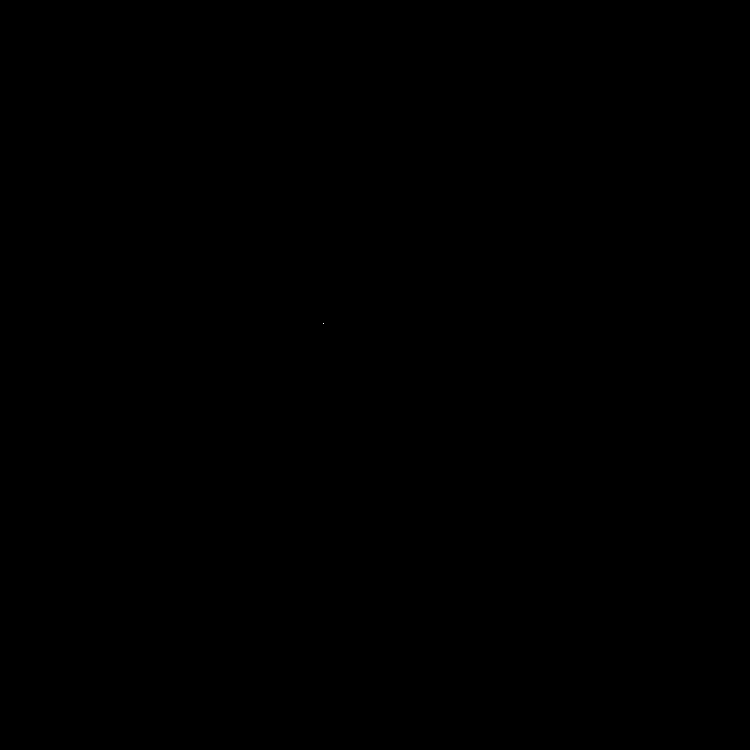
Other square roots can be driven into the script . (You can drive in fractional values).
In the second script, you can drive a sequence manually.
Another script for billiards. The coordinates of the mouse - the size of the pool. The pattern in the left part is formed from the sequence obtained using the residuals from division (details in the previous article). Parity on the right side .
Part 1: Fractals in irrational numbers.

The article contains Gif and contrasting pictures. Epileptic seizures may occur.
In the previous article, we looked at the binary sequence visualization algorithm. Let's remember.
')
Take the binary sequence. As an example, the first few bits of the fractal sequence discussed in the previous article:
0100110110010011001001101100
Draw a square cell field. Set the bits at the upper border. The distance between the bits is two cells:

For each bit, draw a diagonal dotted trajectory (through the cell). For zeros, draw the first stroke to the right:

For units, left:

Draw a trajectory for each bit. Got a "billiard" pattern:

Identical pattern (without a defect along the diagonal - the sequence is infinite, we visualized it as a final sequence) can be obtained in another way. We invert every even bit in the sequence:
0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 1 1 1 1
Next, for each bit, draw vertical dashed lines:

Place bits on the left, draw horizontal lines:

Combine:

After writing the first article, two questions remained unresolved:
1. Is it possible to draw a fractal pattern for irrational numbers? Can. The question was solved in the previous article. The picture above is part of the fractal pattern for . If you select one of the curves on this pattern:

We get the well-known fractal curve - “Fibonacci word fractal”.
2. The second question is whether it is possible to write an algorithm that paints a pattern:

We will deal with the second question in this article. We will color the patterns using a weaving machine, which we will simulate using JavaScript.

In the diagram above - the easiest machine. It consists of two frames through which the threads are stretched. The frames are connected to the pedals. When you press one of the pedals, one of the frames rises. The threads stretched through this frame are raised and a transverse thread is pulled into the resulting gap between the threads. If even and odd threads are pulled through different frames, weaving is obtained in a checkerboard pattern:

In more complex machines, four or more frames are used:

Ashford 4 Shaft Table Loom
In order not to get confused about which pedal to press - they make a scheme.

In the upper right part of the scheme, it is noted which frames the threads pass (the scheme for a loom for 8 frames).
In the upper left corner - which pedals to clamp at the same time (each pedal is connected only with its own frame).
In the left bottom part - in what order to clamp the pedals.
In the lower right - what kind of interweaving we get. If we stretch the white thread through the black we get a monochrome pattern.
Immediately "move" in principle may seem a bit difficult. The picture below shows how the weaving pattern is formed:

Let's write a script. Pull the thread through the frame will be using a one-dimensional array array2. In the one-dimensional array array1 we write the sequence of pedaling. In array3 (8x8 binary array), write down which pedals to clamp at the same time.

for(var i=0;i<length;i++){ for(var j=0;j<length;j++){ if(array3[array1[i]][array2[j]]){ context.fillRect(i, j, 1, 1); } } } Script (works in Google Chrome).
With the help of our improvised loom, we can draw a wide variety of patterns:

But historically, the average person has no more than two legs. Therefore, it is convenient to simultaneously clamp no more than two pedals. One of the most popular patterns for a loom is as follows:

For 4 frames. And its modification for 8 frames:

Suddenly, patterns (or a fragment of patterns) made using this pattern are similar to our "billiard" patterns. In addition, these patterns are shaded:

You can learn how to select "billiard" patterns for the loom. Example:

At the beginning of the article we have already seen a fragment of this pattern.
Finish with looms and write a script to visualize the binary sequences. We can get rid of one of the arrays - the pattern is symmetrical diagonally. How to fill the remaining array? Elementary:

Take the sequence for . Create an array. In the zero element of the array write the zero bit of the sequence. Alternately take every bit of the sequence. If the n-th bit = 1 - write to the array a [n] = a [n-1] +1. If bit = 0, write a [n] = a [n-1] -1

var a=[0]; for(var i=1;i<size;i++){ if(Math.floor(i*Math.sqrt(2))%2==1) a[i]=a[i-1]+1; else a[i]=a[i-1]-1; } Checking:
for(var i=0;i<size;i++){ context.fillRect(i, a[i]+50, 1, 1); } 
In fact, we have already received an elementary fractal, but we will continue.
Next, let's deal with the matrix:

Summarize and . We divide by the module by 4. If the resulting result is = 0 or 1, we write to the matrix true. For 2 and 3, write false. We can do without the matrix (it is not known in advance what the maximum and minimum values are taken by a [n]). Sum the a [x] and a [y]. We add some number to the resulting amount. (to get rid of those cases when the sum is a negative number). Divide modulo 4. For values 0 and 1, paint over a pixel with coordinates and .
The final algorithm takes only a few lines:
var a=[0]; for(var i=1;i<size;i++){ if(Math.floor(i*Math.sqrt(2))%2==1) a[i]=a[i-1]+1; else a[i]=a[i-1]-1; } for(var x=0;x<size;x++){ for(var y=0;y<size;y++){ q=(a[x]+a[y]+512)%4; if(q==0 || q==1) context.fillRect(x, y, 1, 1); } } Visualize our fractal sequences.

You can easily modify the script in order to get an RGB image:
q=(a[x]+a[y]+512)%4; /*if(q==0 || q==1) context.fillRect(x, y, 1, 1);*/ if(q==0) context.fillStyle = 'rgb(255,0,0)'; if(q==1) context.fillStyle = 'rgb(0,255,0)'; if(q==2) context.fillStyle = 'rgb(0,0,255)'; if(q==3) context.fillStyle = 'rgb(0,0,0)'; context.fillRect(x, y, 1, 1); 
Above, we added a certain number to the sum of a [x] + a [y] . If you do not add this number - the minimum value of the sum = -8, maximum = 8 (for and from 0 to 750). If you remove - in some cases, the sum is negative and not a multiple of 4, and for these cases the pixel is not painted (remains black):
q=(a[x]+a[y])%4; if(q==0 || q==1) context.fillRect(x, y, 1, 1); 
It can be imagined as if a part of the fractal is below some imaginary border (below this border only negative values are multiplied by multiples of 4: -4, -8, -12, ...).
We can see where this border is:
if(a[x]+a[y]>=0) context.fillRect(x, y, 1, 1); 
Instead of dividing by module, we can compare the sum with a certain specific value and thus paint over only one “layer” of the fractal. As an example, take the average between the minimum and maximum values:
q=(a[x]+a[y]); if(q==0) context.fillRect(x, y, 1, 1); 
If not clear

By changing the values from minimum to maximum, we can see how the “layers” change over time:

If not clear
I strongly recommend not opening a spoiler if you have epilepsy

In addition, we can “head on” compare a [x] with a [y] and also get a fractal pattern:
if(a[x]==a[y]) context.fillRect(x, y, 1, 1); 
The following sequence:
Fractal:

RGB:

Middle layer:

In dynamics:

Fractal:

RGB:

Middle layer:

In dynamics:

Fractal:

RGB:

Middle layer:

In dynamics:
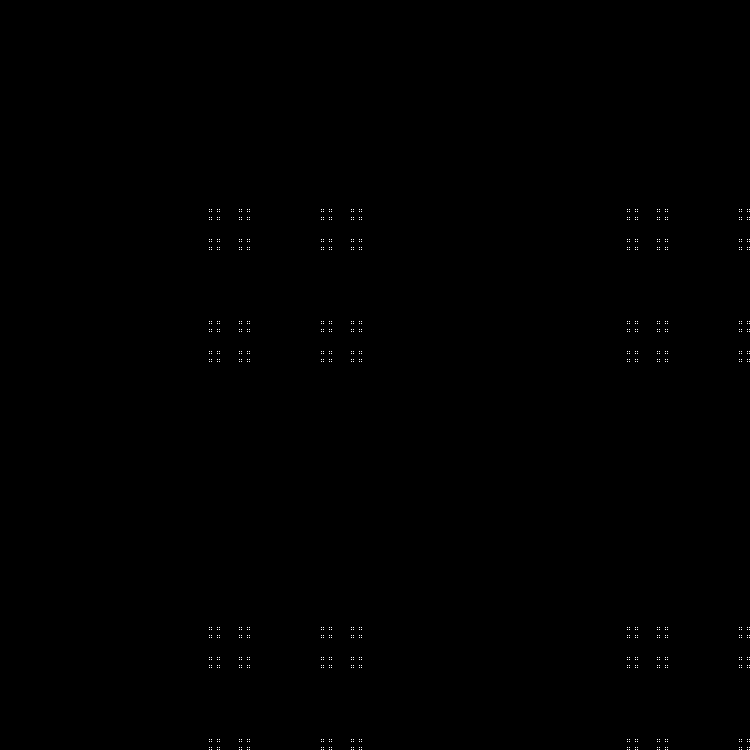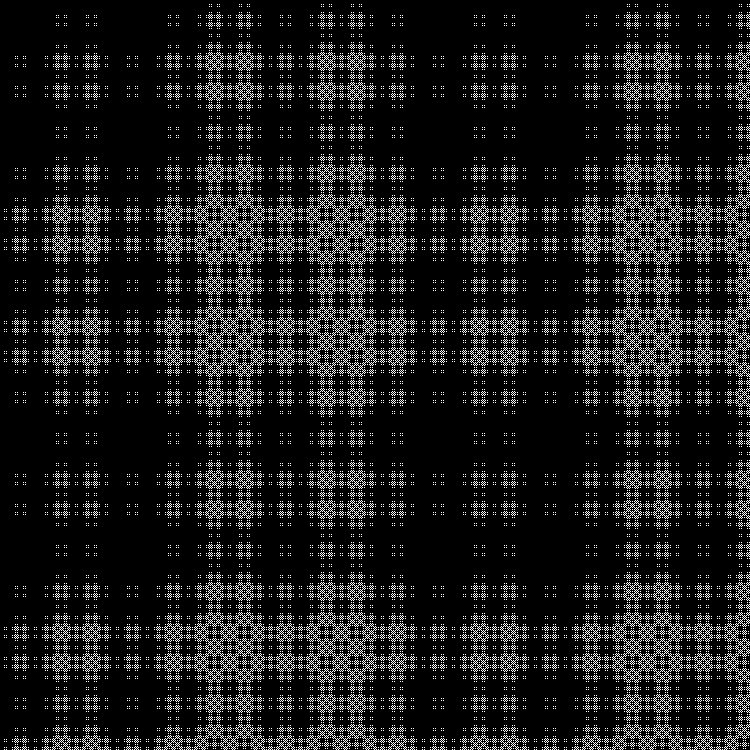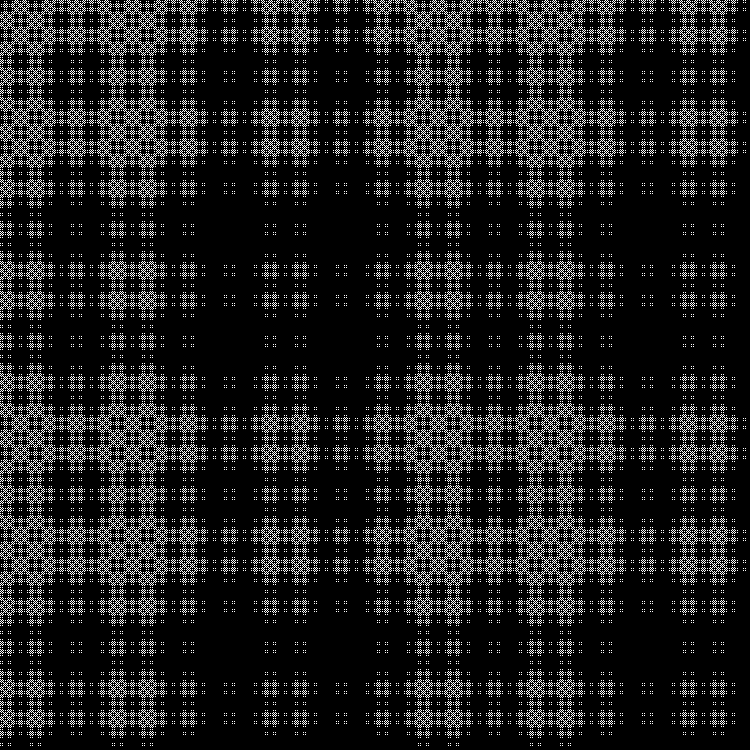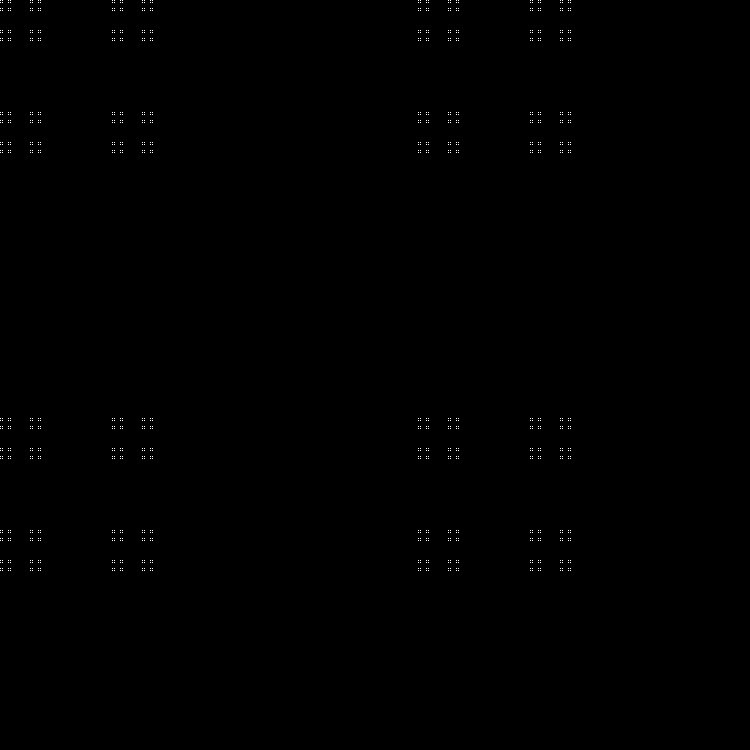
Fractal:

RGB:

Middle layer:

In dynamics:

Well, our favorite fractal (part of this pattern can be drawn using billiards, with the sides equal to Fibonacci numbers):
Fractal:

RGB:

Middle layer:

In dynamics:
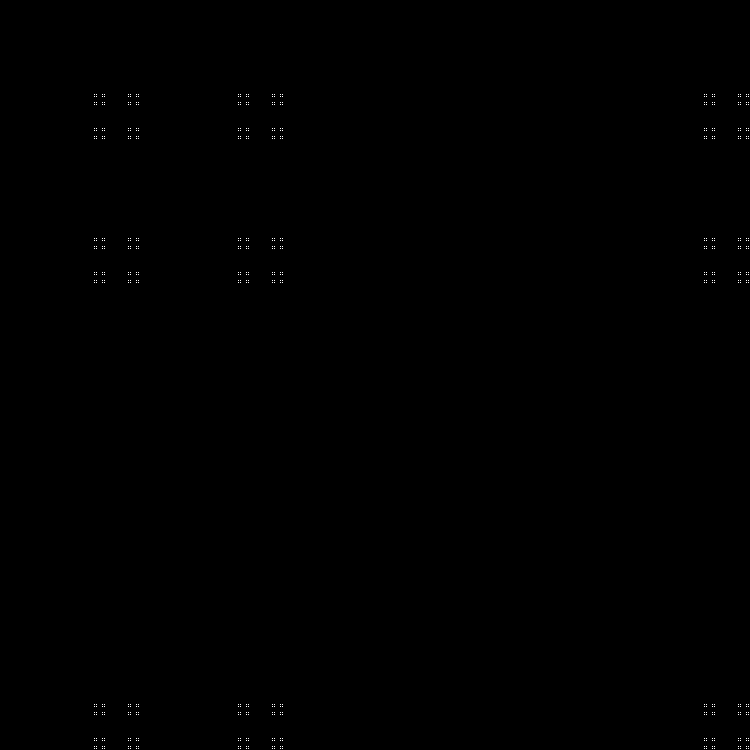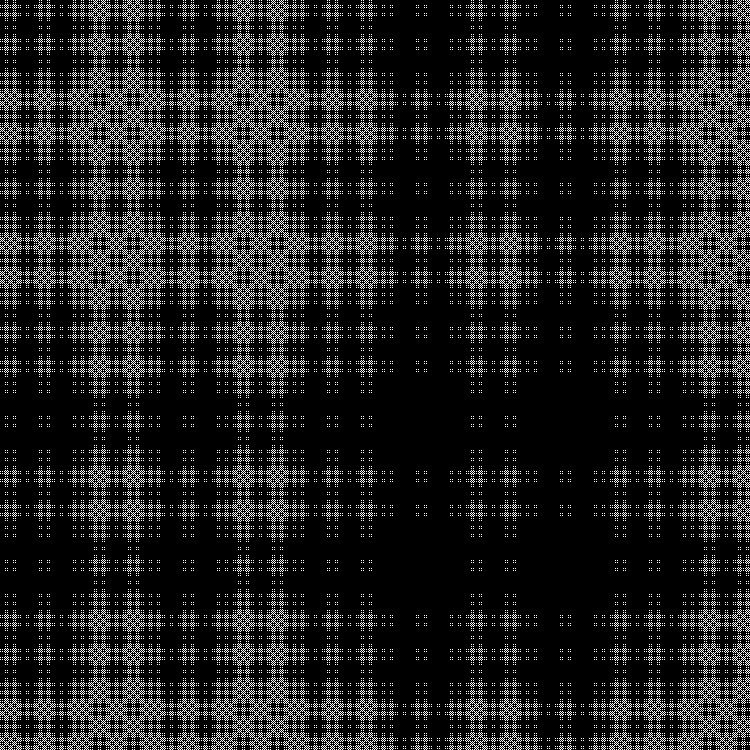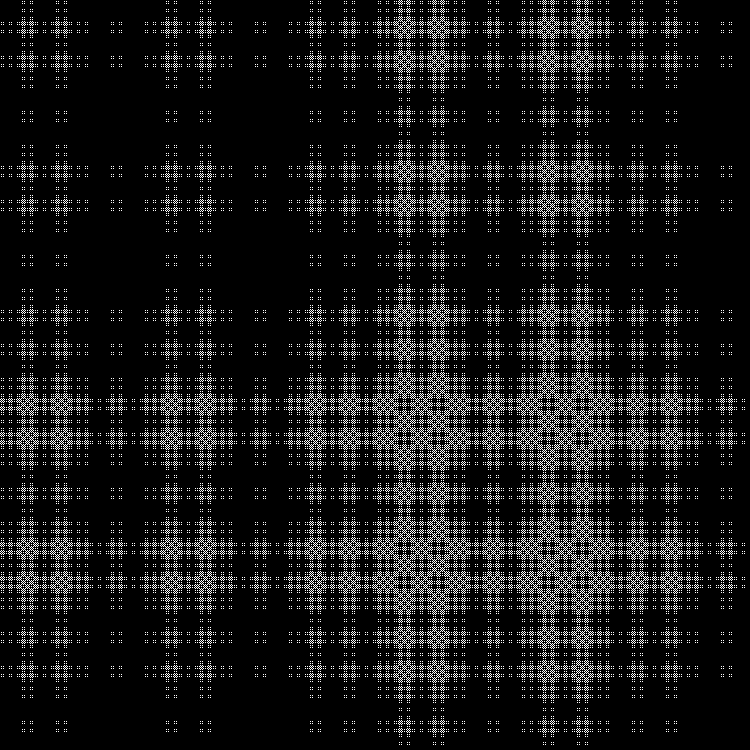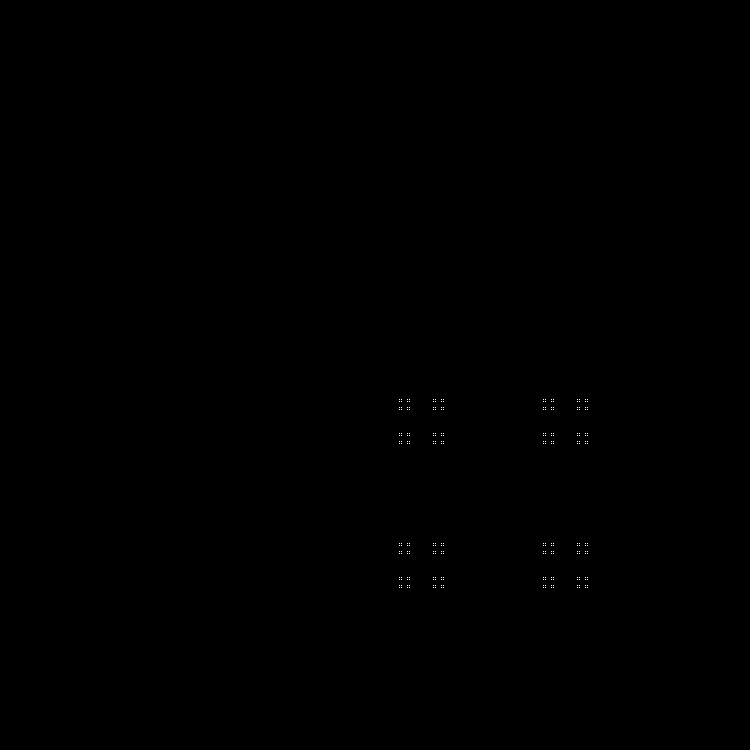
Another sequence to complete:
Pattern:

RGB:

Middle layer:

In dynamics:
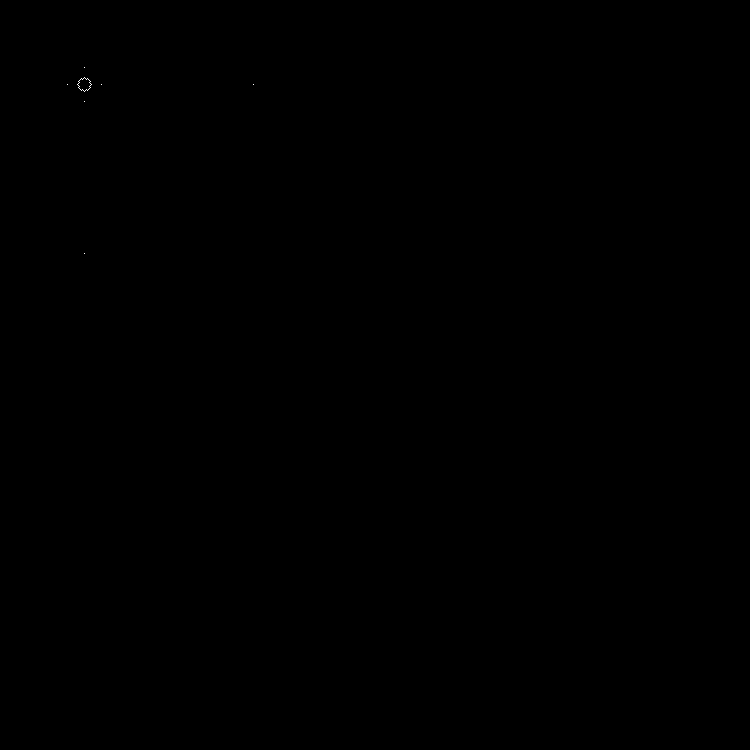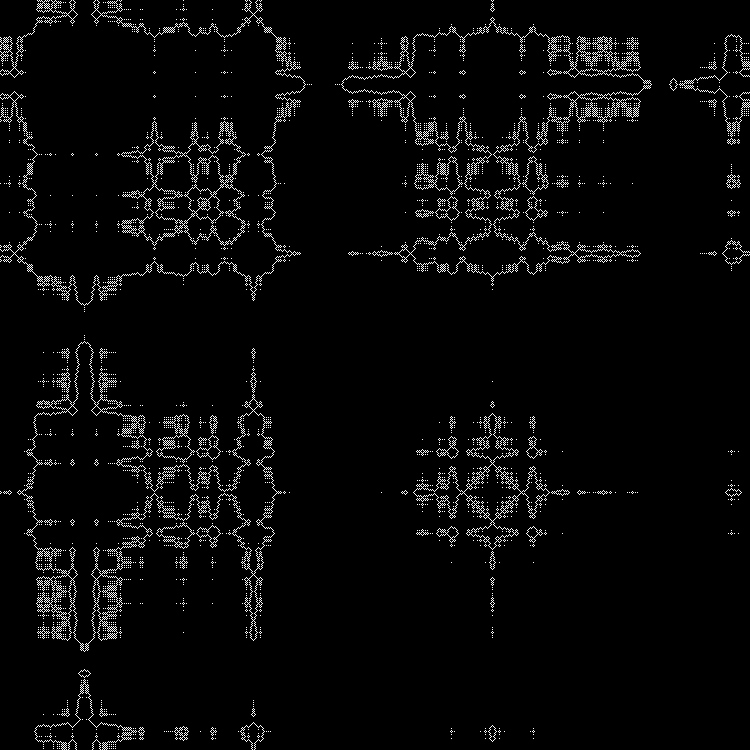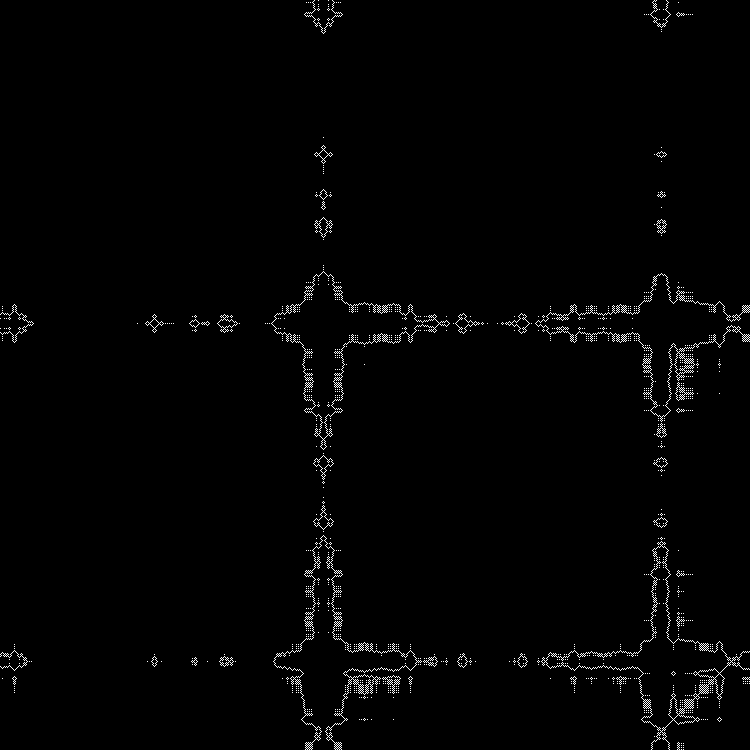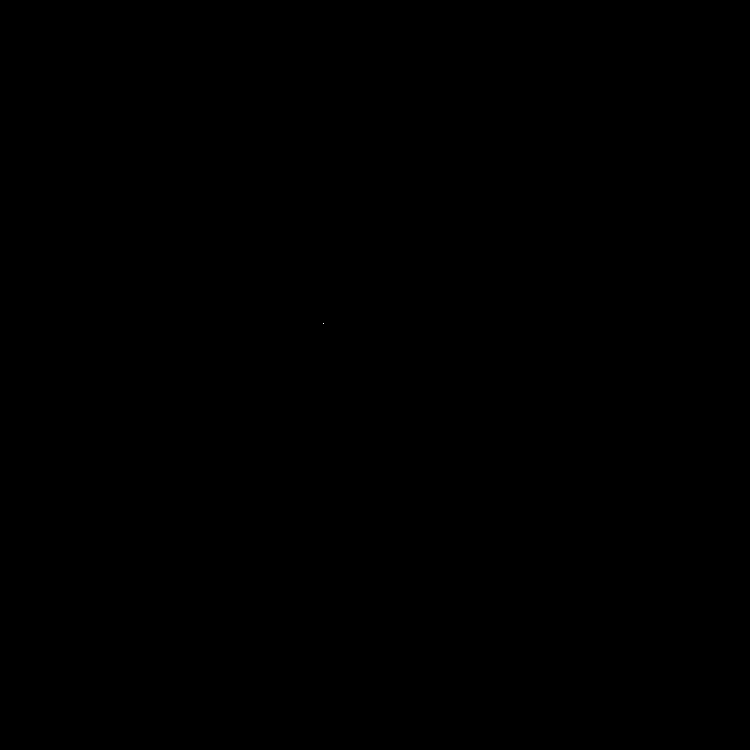
Other square roots can be driven into the script . (You can drive in fractional values).
In the second script, you can drive a sequence manually.
Another script for billiards. The coordinates of the mouse - the size of the pool. The pattern in the left part is formed from the sequence obtained using the residuals from division (details in the previous article). Parity on the right side .
Source: https://habr.com/ru/post/447326/
All Articles