Consciousness and Doomsday Argument

Once upon a time there was a sailor. He had two beloved women in different ports, and he wanted children - he just did not decide one or two. He decided to throw a coin. Eagle - there will be one child from one of the women (to which she will go first to the port for work - that's how it will turn out), tails will make every woman for the child. It is not known how the coin fell, and how fate threw him around the world, but you are his child. What is the probability that you are his only child?

Let's think about it. An honest coin gives a probability of this 1/2. But is it so obvious? After all, if tails fell, then “you”, those who can be asked a question, like three: a lonely child if an eagle fell, and two - if tails fell. So the probability is 1/3. Not obvious? Let me reformulate the problem so that the second answer is more obvious.

Sleeping Beauty Task

')
The beauty participates in the experiment: on Sunday, the experimenters, in secret from her, throw a coin. If an eagle falls, then it is put to sleep, wake up on Monday, then put to sleep again. She wakes up on Wednesday and the experiment ends. If tails fall out, they wake her up on Monday too, but then erase her memory and put her to sleep, and wake up again on Tuesday. They are again put to sleep (already without erasing the memory) and waking up completely on Wednesday.

So, the beauty is awakened (either on Monday, or on Tuesday). She is asked a question: what do you think, what is the probability that today is Tuesday? The coin is fair, so the probability is 1/2. But a second, on Monday, she is woken up twice as often as on Tuesday !!! So the probability is 1/3.



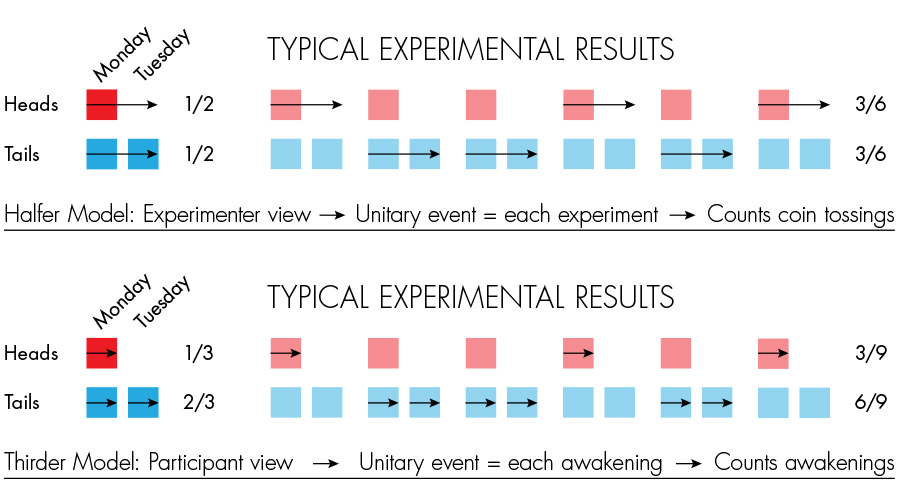
In the description of the paradox you can read that both solutions are correct, and this is true, but the rabbit hole leads much deeper. She shares two schools of thought , Self Sampling Assumption (SSA) and Self indication Assumption (SIA) . Written in English, because even the articles themselves on the wiki exist only in English (only in one language, which is rare). If you come up with beautiful translations of these terms into Russian, write in the comments.

Self Sampling Assumption

SSA sounds like this: For all equal, the observer must assume that he is selected at random from among a multitude of observers like him who have ever existed, or will exist.

That is, the SSA principle is built on a fairly reasonable basis that the observer should not consider himself “chosen” - either in time or in space. SSA gives the answer 1/2 for the sleeping beauty task.

Consider how SSA works by example. Most of all, the work of SSA resembles the incarnation of the soul into a randomly chosen body, and there is no time for the soul (eternalism), and it can incarnate into the body at any time. Take a graph of the population of the earth at different times.



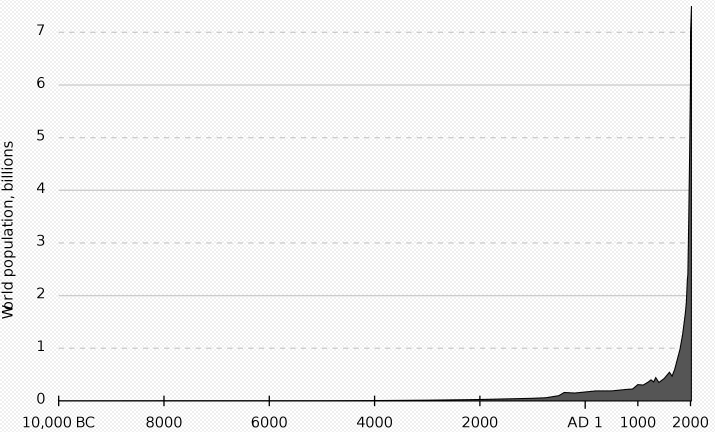
We randomly throw a dart at any place in the shaded area. Do you notice more painted over to the right? Most likely your dart will get to the right side of the chart due to the almost exponential growth of the population of the Earth. So, if you live, then most likely you live closer to the end of the world. This is called the Doomsday Argument .

Self Indication Assumption

It is difficult to argue with the Doomsday argument - this statement logically follows from the SSA axioms. Therefore, to save the world, it is necessary to change this axiomatics! SIA, as opposed to SSA, argues that: For all equal, the observer must assume that he is chosen randomly from the set of all possible observers.

What is the fundamental difference with SSA? I will try to explain it in my own language, since the Wiki article is rather indistinct, and basically indicates that SIA gives the answer 1/3 in paradoxes about the sleeping beauty and the sailor's child. So, with SSA, your soul moves into one of the bodies in the physical world, and their set is considered predetermined (if you stand on the positions of eternalism). SIA is repelled from the opposite: from your existence. If you exist in this form, then most likely, this is a good configuration, and, therefore, it is reasonable to expect that there are many such configurations. That is, your incarnation says that it is likely in this world.

I have a feeling that SIA runs automatically in a multiverse. SIA struggles with the argument of the Doomsday roughly speaking: if we exist and there were so many people before us, then the existence of even more people is even more likely. That is, your position n in the series of births does not indicate how many people will be born in total. I recommend reading about how SIA is struggling with the doomsday argument , and here I’ll just write out the vocabulary used in the article: souls harboring, humans, fish .



However, there are many formulas. However, let us dwell on what the intuition says. You know that your bag lies in a dark room of an indefinite size (a room can even be a kilometer long!), And it is thrown there in a random place. You open the door ...



... and see your bag a meter from the door. You can conclude that with considerable probability, a room no longer than 15–20 meters, and very unlikely a kilometer long. Agree, it is quite reasonable?

Great Filter: Doomsday Strikes Back

It turns out with SIA we get out of the fire and into the fire, if we remember the Great Filter .

Probably on the way with many stages - the emergence of life, the emergence of multicellular life, the emergence of the mind, the galactic expansion of the mind, and so on. (only 9 stages, see the link) at least one of the stages is extremely difficult and often life either dies or is at an impasse on reaching this difficult stage. Accordingly, the filter can be either early (for example, the very emergence of life) or late (galactic expansion or death from robots, for example. Obviously, the fact that we exist, according to SIA, says that the filter is late , which means it is soon :



In general, the filter works in a very interesting way. Imagine a princess. In order to win her hand and heart, the applicant must open seven boxes with combination locks in an hour. At the first box, the password consists of only one digit, and the average time for selecting a password is only one tenth of a minute. The second box has two digits, the average opening time is 1 minute. At the third - 10 minutes, 100 minutes, 1000 minutes, 10,000 minutes and the last 100,000 minutes (about 70 days). I remind you that you need to catch all the boxes in an hour, and losers will die. However, the princess is so beautiful that the queue of those who want to tempt fate, does not dry out:



Sooner or later, one of the applicants stupidly lucky. How long did it take him to open each of the 7 boxes? Obviously

$$

But what times will be characteristic? Intuition says that the first three numbers will be, as expected, small, but for complex tasks it will be $$ . But intuition deceives us. You should expect about such times: 0.1, 0.9, 1, 2, 15, 17, 16, 16 - of course, the numbers can vary, but the execution time of very simple tasks will be close to the average, the time of tasks with average complexity will be slightly reduced, but the execution time of unrealistically complex tasks will be approximately the same and equal

(60-time simple and medium tasks) / number of difficult stages.

This observation belongs to Nick Bostrom and, I confess, I did not believe his conclusions until I wrote a small simulator and drove him.

From this we can make a strange conclusion - by observing the history of the origin of life on Earth, we observe a number of stages that took a very long time (for example, the emergence of eukaryotes, photosynthesis, the emergence of multicellular life). This suggests that these stages are complex, but does not tell us anything about the relative complexity of these stages. But the emergence of the mind, obviously, the stage is simple - and the mind develops in parallel in a large number of species, if not man, then 10-20-50 million years, and someone else would launch the rocket.

A few paradoxes from Bostrom

Here it is. Bostrom seriously considers both SSA and SIA. However, a number of “extreme cases” may look very strange. Bostrom calls these cases the paradox of Adam and Eve, the first living people. As you remember, by the SSA, the soul can move into any body, and it’s almost unbelievable that you should be among the first two living people. Nick's word:

Tip of the Serpent. One day, the Serpent crawled up to the couple and hissed: “Shhhhhhh ... If you love each other, then either Eve will have a child or not. If she gives birth, you will be the first of billions of people. But the conditional probability of being the first people in the chain of births is very small. On the other hand, if Eve does not become pregnant, then only two people will be in total, and the probability of being the first two of two people is 100%. According to the Baes theorem, the risk of becoming pregnant with Eva is less than one billionth! So enjoy each other and do not think about the consequences! ”

The paradox of a deer. Due to the fact that Adam and Eve did not grow old in paradise, they had time to invent a way to raise a baby from a test tube, with a 100% guarantee. But Adam is tired of hunting every day. He decides with Eve: if the wounded deer does not come to him today, then tomorrow they will make a child. Now, according to the SSA, Adam can almost be absolutely certain that the wounded deer will soon come to them in the cave, and it will only have to be finished off.

Oddly enough, even in our time there is an opportunity to conduct an experiment and check the SSA.

UN ++. In 2100, an all-powerful and united world government was formed: UN ++. Any UN ++ solution is exactly executed. But the world is still powerless against external threats - for example, supernova explosions that can destroy our world entirely. Moreover, scientists have found nearby n stars ready to explode. The ray from the explosion of each supernova with a probability of 10% can greatly damage the Earth (but not completely destroy life). But UN ++ makes this decision: for every threat in the list, if it happens, UN ++ will create colonies in space, where the number of people will exceed the number of people that will ever live on Earth by m times. If m >> n, then we can be sure that the supernova explosions will not affect the Earth.

Boltzmann Brain

This story happened a long time ago, in the 19th century. About the big bang and the end time of the Universe existence nothing was known, and this gave rise to the problem: if the Universe existed always (as it was then thought), then thermal death had to comprehend it long ago, the temperature everywhere would have leveled off, and life would be impossible.

Boltzmann saw the following solution: if the Universe is infinite and there is infinite time, then sooner or later an arbitrarily large fluctuation will arise in it. We live in such a way. However, since the probability of fluctuations rapidly decreases with an increase in its size, it is much more likely to assume that it was not a bubble the size of the visible Universe, but only a human brain with a memory of how it supposedly lived:



The next second, the hot gas will absorb this brain. Boltzmann understood this and therefore committed suicide. We know that problems as they were thought of in the 19th century are not — the Universe has been developing from a state with very low entropy for 14 billion years. But the idea of ​​the Boltzmann brain is not forgotten. In philosophy, such brains are called “ freak observer ”. Indeed, take, for example, the cosmological model, which is called “ Eternal Inflation ”:



Let the majority of bubbles have poorly tuned parameters of the “Standard Model” and life there is either impossible to develop or almost impossible (but freak observers are possible). And the likelihood that there will be a universe, like ours, is negligible. But then the number of freak observers would exceed the number of real ones, and we rather had a chance to incarnate in the form of the Boltzmann brain, which is not happening. So, the probability of life is not so low. However, with a multiverse we enter a completely unfamiliar territory.

Sampling in MWI

In the comments to my article , an interesting dispute about quantum immortality unfolded. But can we solve it without understanding how sampling in MWI works? SIA, for example, refers to “all possible observers”. But should we just count the branches or take into account the “weight” / probability of these branches according to the Born rule? I think we should, let's call it Born-Adjusted-SIA, or B-SIA. For the sleeping beauty case, the B-SIA makes a difference with the SIA if the coin falls out with a probability other than 1/2.

But the MWI branches themselves are too small — for example, the logical state of the processor does not depend on the state of an individual electron (except for possible bifurcation points), otherwise it would be too susceptible to thermal noise. So, when we talk about the state of the processor, we are talking about a whole ensemble of MWI branches. Similarly, is a brain condition a single branch of MWI or a bundle of logically equivalent brain states? (but can these branches break up in the future)? Is consciousness connected with the constant bifurcation of stories associated with these branches?

Sampling in infinite universe

If you do not believe in MWI, then this will not save you. Enough to believe in an infinite universe. Indeed, according to Bekenstein’s limit , the number of states in which matter can exist in a certain volume (sphere) is of course proportional to the area of ​​the sphere (and not its volume!).

It follows two interesting conclusions:

If you create the infinite Universe, then generating its fragments sooner or later you will run out of unique combinations, as if you were collecting the world from Lego. Therefore, if you exist, then you exist in an infinite number of copies. If these copies are in the same condition, then is their consciousness common or not? We do not know. Consciousness is such an incomprehensible object that I cannot even define the operation of equality on it.

Secondly, the ratio of the area of ​​the sphere to its volume (and the mass of matter inside) decreases with increasing radius of this sphere. That is, the more we take matter, the simpler it is (because there are inevitable correlations and “confusion” inside). In the limit, the density of matter in the infinite universe must be zero! But this is not surprising - if Max Tegmark is right , as it should be - in the theory of the mathematical Universe there is no information related to the initial conditions, which means that the deterministic development of the multiverse preserves the zero amount of information originally given.

As you can see, even with TOE we still have too much to learn, and we didn’t even tackle these topics. For example, I missed Strong Self Sampling Assumption - Google it! But won't we have to weaken some scientific principles, for example, the principle of falsifiability? Quite possible.

Participate in polls, please. $$