Exotic data structures: Modified Merkle Patricia Trie

“What the devil should I remember by heart all these damn algorithms and data structures?”

Approximately the comments of most articles about the passage of technical interviews boil down to this. The main thesis, as a rule, is that everything that has been used one way or another has already been implemented ten times and is most unlikely to have to deal with this ordinary programmer. Well, to some extent this is true. But, as it turned out, not everything was implemented, and unfortunately (or fortunately?), I still had to create the Data Structure.

Mysterious Modified Merkle Patricia Trie.

Since there is no information about this tree at all in Habré, but a little more on the medium, I want to tell about what kind of beast it is and what it is eaten with.

What is it?

Disclaimer: The main source of information in the implementation for me was Yellow paper , as well as the source codes of parity-ethereum and go-ethereum . There was a minimum of theoretical information about the substantiation of certain decisions; therefore, all conclusions concerning the reasons for the adoption of certain decisions are my personal ones. In case I am mistaken in something, I will be glad to fix it in the comments.

A tree is a data structure representing a connected acyclic graph. Everything is simple, everyone is familiar with it.

A prefix tree is a root tree in which you can store key-value pairs due to the fact that the nodes are divided into two types: those that contain part of the path (prefix), and end nodes that contain the stored value. A value is present in the tree if and only if, using the key, we can go all the way from the root of the tree and at the end find a node with a value.

A PATRICIA tree is a prefix tree in which the prefixes are binary — that is, each key node stores information about one bit.

A Merkla tree is a hash tree built over some kind of data chain that aggregates these same hashes into one (root) that stores information about the state of all data blocks. That is, the root hash is a kind of "digital signature" of the state of a chain of blocks. This thing is used actively in the blockchain, and you can read more about it here .

Total: Modified Merkle Patricia Trie (hereinafter referred to as MPT for short) is a hash tree that stores key-value pairs, with the keys represented in binary form. And what exactly is "Modified" we will find out a little later when we discuss the implementation.

Why is this?

MPT is used in the Ethereum project to store data about accounts, transactions, results of their execution and other data necessary for the functioning of the system.
Unlike Bitcoin, in which the state is implicit and is calculated by each node independently, the balance of each account (as well as its associated data) is stored directly in the blockchain. Moreover, the location and immutability of data should be provided cryptographically - few people will use a cryptocurrency, in which the balance of a random account can change without objective reasons.

The main problem faced by the developers of Ethereum is the creation of a data structure that allows you to effectively store key-value pairs and at the same time provide verification of stored data. This is how MPT appeared.

Like this?

MPT is a prefix PATRICIA-tree, in which the keys are sequences of bytes.

The edges in this tree are sequences of nibbles (halves of bytes). Accordingly, one node can have up to sixteen descendants (corresponding to branches from 0x0 to 0xF).

Nodes are divided into 3 types:

• Branch node. The node used for branching. Contains up to 1 to 16 references to child nodes. May also contain a value.
• Extension node. An auxiliary node that stores some part of the path that is common to several child nodes, as well as a link to the branch node that lies further.
• Leaf node. The node containing the path part and the stored value. Is finite in the chain.

As already mentioned, MPT is built on top of another kv-storage, in which the nodes are stored in the form of "link" => " RLP encoded node".

And here we meet with a new concept: RLP. In short, this is a method of encoding data that is lists or byte sequences. Example: [ "cat", "dog" ] = [ 0xc8, 0x83, 'c', 'a', 't', 0x83, 'd', 'o', 'g' ] . I will not go into details in particular, and in the implementation I use the ready-made library for this, since the coverage of this topic will also inflate an already rather big article too. If you're still interested, in more detail you can read here . We limit ourselves to the fact that we can encode the data in the RLP and decode it back.

The link to the node is defined as follows: in case the length of the RLP encoded node is 32 or more bytes, then the link is keccak hash from the RLP -representation of the node. If the length is less than 32 bytes, then the link itself is the RLP representation of the node.

Obviously, in the second case, saving the node to the database is not necessary, since it will be entirely stored inside the parent node.

The combination of three types of nodes allows you to efficiently store data even when there are few keys (then most of the paths will be stored in the extension and leaf nodes, and there will be few branch nodes), and in the case of a lot of nodes (the paths will not be explicitly stored, and will be "collected" during the passage of the branch nodes).

A complete example of a tree using all kinds of nodes:

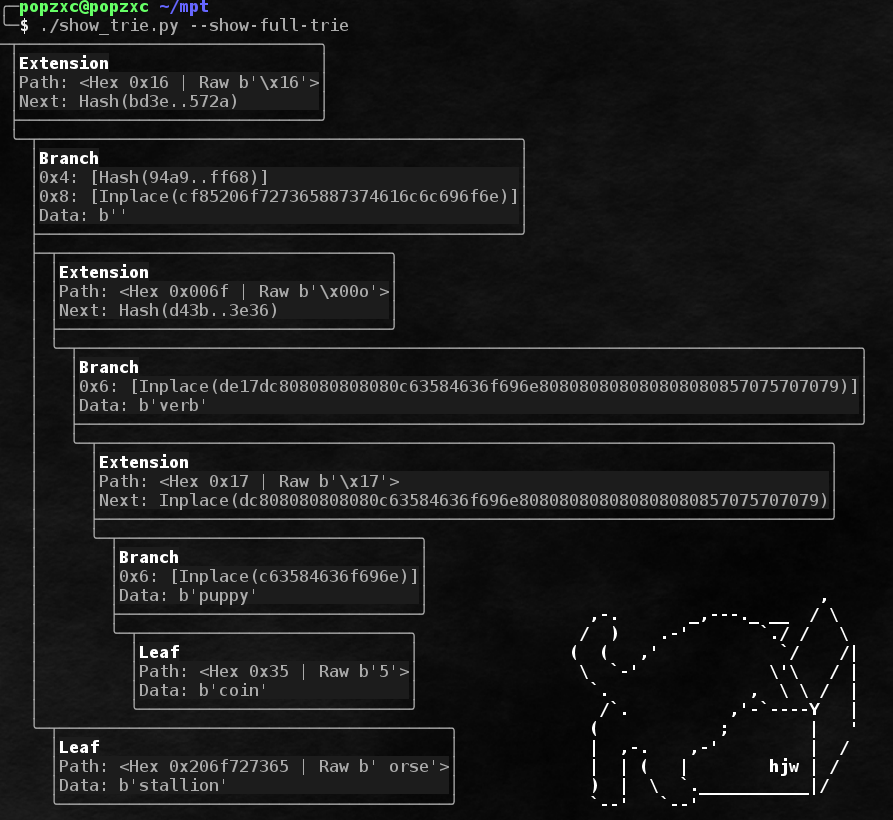
As you can see, the stored parts of the paths have prefixes. Prefixes are needed for several purposes:

1. To distinguish extension nodes from leaf nodes.
2. To align sequences consisting of an odd number of nibbles.

The rules for creating prefixes are very simple:

• The prefix takes 1 nibble. If the path length (excluding the prefix) is odd, then the path starts immediately after the prefix. If the path length is even, then nibble 0x0 is added first to align after the prefix.
• The prefix is ​​initially 0x0.
• If the length of the path is odd, then 0x1 is added to the prefix, if even is 0x0.
• If the path leads to a Leaf node, then 0x2 is added to the prefix, and 0x0 to the Extension node.

On bitik, I think it will be clearer:

 0b0000 =>  , Extension  0b0001 =>  , Extension  0b0010 =>  , Leaf  0b0011 =>  , Leaf  

Delete that is not delete

Despite the fact that the tree has the operation of deleting nodes, in fact, everything that was once added remains in the tree forever.

This is necessary in order not to create a full tree for each block, but to store only the difference between the old and the new version of the tree.

Accordingly, using different root hashes as an entry point, we can get any of the states in which the tree has ever been.

This is not all optimization. There is more, but we will not talk about it - and so the article is big. However, you can read it yourself.

Implementation

With theory over, go to the practice. We will use the lingua franca from the IT world, I mean python .

Since there will be a lot of code, and for the format of the article, much will have to be reduced and divided, I will immediately leave a link to github .
If necessary, there you can look at the whole picture.

First, let's define the interface of the tree that we want to get as a result:

 class MerklePatriciaTrie: def __init__(self, storage, root=None): pass def root(self): pass def get(self, encoded_key): pass def update(self, encoded_key, encoded_value): pass def delete(self, encoded_key): pass 

The interface is extremely simple. Available operations are getting, deleting, inserting and modifying (combined in an update), as well as getting the root hash.

The storage will be transferred to the __init__ method - a dict like data structure in which we will store the nodes, and also root - the "vertex" of the tree. If None is transferred as root , we assume that the tree is empty and we are working from scratch.

_Remark: you may wonder why variables in methods are named as encoded_key and encoded_value , and not just key / value . The answer is simple: by specification, all keys and values ​​must be encoded in the RLP . We will not bother ourselves with this, and we will leave this task on the shoulders of library users.

However, before we proceed to the implementation of the tree itself, it is necessary to do two important things:

1. Implement the NibblePath class, which is a chain of nibbles, so as not to encode them manually.
2. Implement the Node class and within this class - Extension , Leaf and Branch .

NibblePath

So, NibblePath . Since we will actively move around the tree, the basis of the functionality of our class should be the ability to set the "offset" from the beginning of the path, as well as receive a specific nibble. Knowing this, we define the basis of our class (as well as a couple of useful constants for working with prefixes below):

 class NibblePath: ODD_FLAG = 0x10 LEAF_FLAG = 0x20 def __init__(self, data, offset=0): self._data = data # ,   . self._offset = offset #      def consume(self, amount): # "" N      . self._offset += amount return self def at(self, idx): #      idx = idx + self._offset #    ,   ,    , #   ,    -      . byte_idx = idx // 2 nibble_idx = idx % 2 #   . byte = self._data[byte_idx] #      . nibble = byte >> 4 if nibble_idx == 0 else byte & 0x0F return nibble 

It's pretty simple, isn't it?

It remains to write only functions for encoding and decoding a sequence of nibbles.

 class NibblePath: # ... def decode_with_type(data): #   : # ,     ,    . is_odd_len = data[0] & NibblePath.ODD_FLAG == NibblePath.ODD_FLAG is_leaf = data[0] & NibblePath.LEAF_FLAG == NibblePath.LEAF_FLAG #    ,     #    . offset  , #       "" . offset = 1 if is_odd_len else 2 return NibblePath(data, offset), is_leaf def encode(self, is_leaf): output = [] #    ,       . nibbles_len = len(self._data) * 2 - self._offset is_odd = nibbles_len % 2 == 1 #  . prefix = 0x00 #    ,    . #      (self.at(0))     . #           (0x0). prefix += self.ODD_FLAG + self.at(0) if is_odd else 0x00 #  ,  Leaf node,  . prefix += self.LEAF_FLAG if is_leaf else 0x00 output.append(prefix) # ,      ,  . pos = nibbles_len % 2 #          , #     2 ,    , #     , #    . while pos < nibbles_len: byte = self.at(pos) * 16 + self.at(pos + 1) output.append(byte) pos += 2 return bytes(output) 

In principle, this is the minimum necessary for convenient work with nibbls. Of course, in the present implementation there are some more auxiliary methods (such as combine , merging two paths into one), but their implementation is rather trivial. If interested - the full version can be found here .

Node

As we already know, nodes are divided into three types: Leaf, Extension, and Branch. All of them can be encoded and decoded, and the only difference is the data that is stored inside. To be honest, this is how algebraic data types are requested, and on Rust , for example, I would write something in the spirit of:

 pub enum Node<'a> { Leaf(NibblesSlice<'a>, &'a [u8]), Extension(NibblesSlice<'a>, NodeReference), Branch([Option<NodeReference>; 16], Option<&'a [u8]>), } 

However, there is no ADT as such in Python, so we will define the Node class, and inside it there will be three classes corresponding to the node types. Encoding is implemented directly in the node classes, and decoding is implemented in the Node class.

The implementation, however, is elementary:

Leaf:

 class Leaf: def __init__(self, path, data): self.path = path self.data = data def encode(self): #    --    , #   -  ,   -  . return rlp.encode([self.path.encode(True), self.data]) 

Extension:

 class Extension: def __init__(self, path, next_ref): self.path = path self.next_ref = next_ref def encode(self): #    --    , #   -  ,   -    . next_ref = _prepare_reference_for_encoding(self.next_ref) return rlp.encode([self.path.encode(False), next_ref]) 

Branch:

 class Branch: def __init__(self, branches, data=None): self.branches = branches self.data = data def encode(self): #    --    ,  #  16 -     (  ), #   -   (  ). branches = list(map(_prepare_reference_for_encoding, self.branches)) return rlp.encode(branches + [self.data]) 

Everything is very simple. The only thing that can cause questions is the _prepare_reference_for_encoding function.

Here I confess, I had to use a small crutch. The fact is that the rlp library rlp decodes the data recursively, and the link to another node, as we know, can be rlp data (in case the length of the encoded node is less than 32 characters). Working with links in two formats - hash bytes and a decoded node is very inconvenient. Therefore, I wrote two functions that, after decrypting a node, return links to byte format, and before saving, if necessary, decode them. These functions are:

 def _prepare_reference_for_encoding(ref): #    ( ,   ) --  . #       :) if 0 < len(ref) < 32: return rlp.decode(ref) return ref def _prepare_reference_for_usage(ref): #     -   . #          . if isinstance(ref, list): return rlp.encode(ref) return ref 

Finish with nodes by writing a Node class. It will be only 2 methods: decode the node and turn the node into a link.

 class Node: # class Leaf(...) # class Extension(...) # class Branch(...) def decode(encoded_data): data = rlp.decode(encoded_data) # 17  -  Branch . if len(data) == 17: branches = list(map(_prepare_reference_for_usage, data[:16])) node_data = data[16] return Node.Branch(branches, node_data) #    17,   2.   - . #      ,     . path, is_leaf = NibblePath.decode_with_type(data[0]) if is_leaf: return Node.Leaf(path, data[1]) else: ref = _prepare_reference_for_usage(data[1]) return Node.Extension(path, ref) def into_reference(node): #    . #      32 , #   -   . #       . encoded_node = node.encode() if len(encoded_node) < 32: return encoded_node else: return keccak_hash(encoded_node) 

Break

Fuh! There is a lot of information. I think it's time to rest. Here is another cat:

Milota, right? Okay, back to our trees.

MerklePatriciaTrie

Hooray - auxiliary elements are ready, go to the most delicious. Just in case, let me remind the interface of our tree. At the same time, we implement the __init__ method.

 class MerklePatriciaTrie: def __init__(self, storage, root=None): self._storage = storage self._root = root def root(self): pass def get(self, encoded_key): pass def update(self, encoded_key, encoded_value): pass def delete(self, encoded_key): pass 

But we will deal with the remaining methods one by one.

get

The get method (as, in principle, the other methods) will consist of two parts. The method itself will produce data preparation and bring the result to the expected form, whereas the present work will occur within the auxiliary method.

The basic method is extremely simple:

 class MerklePatriciaTrie: # ... def get(self, encoded_key): if not self._root: raise KeyError path = NibblePath(encoded_key) #       #  ,    ,    . result_node = self._get(self._root, path) if type(result_node) is Node.Extension or len(result_node.data) == 0: raise KeyError return result_node.data 

However, _get not too difficult: in order to get to the desired node, we need to go all the way from the root. If at the end we found a node with data (Leaf or Branch) - hurray, the data is received. If it was not possible to pass, then the required key is missing in the tree.

Implementation:

 class MerklePatriciaTrie: # ... def _get(self, node_ref, path): #      . node = self._get_node(node_ref) #    --   . #   ,      . if len(path) == 0: return node if type(node) is Node.Leaf: #     Leaf-,     , #      . if node.path == path: return node elif type(node) is Node.Extension: #    -- Extension,    . if path.starts_with(node.path): rest_path = path.consume(len(node.path)) return self._get(node.next_ref, rest_path) elif type(node) is Node.Branch: #    -- Branch,     . #   ,           #  :      . branch = node.branches[path.at(0)] if len(branch) > 0: return self._get(branch, path.consume(1)) #    ,        , #     . raise KeyError 

Well, at the same time we will write methods for saving and loading nodes. They are simple:

 class MerklePatriciaTrie: # ... def _get_node(self, node_ref): raw_node = None if len(node_ref) == 32: raw_node = self._storage[node_ref] else: raw_node = node_ref return Node.decode(raw_node) def _store_node(self, node): reference = Node.into_reference(node) if len(reference) == 32: self._storage[reference] = node.encode() return reference 

update

The update method is more interesting. Just go to the end and insert Leaf-node will not always. It is quite possible that the key separation point will be somewhere inside the already saved Leaf or Extension node. In this case, you will have to separate them and create several new nodes.

In general, all the logic can be described by the following rules:

1. While the path completely coincides with the already existing nodes, recursively descend the tree.
2. If the path is over and we are in the Branch or Leaf node, then update simply updates the value corresponding to the given key.
3. If the paths are divided (that is, we do not update the value, but insert a new one), and we are in the Branch node — create a Leaf node and indicate a link to it in the corresponding branch of the Branch node.
4. If the paths are divided and we are in the Leaf or Extension node - we need to create a Branch node separating the paths, and also, if necessary, an Extension node for the common part of the path.

Let's gradually express this in code. Why gradually? Because the method is large and it will be hard to understand it in a crowd.
However, I will leave the link to the full method here .

 class MerklePatriciaTrie: # ... def update(self, encoded_key, encoded_value): path = NibblePath(encoded_key) result = self._update(self._root, path, encoded_value) self._root = result def _update(self, node_ref, path, value): #       (,   ), #       . if not node_ref: return self._store_node(Node.Leaf(path, value)) #          #    . node = self._get_node(node_ref) if type(node) == Node.Leaf: ... elif type(node) == Node.Extension: ... elif type(node) == Node.Branch: ... 

Common logic is quite small, all the most interesting is inside if s.

if type(node) == Node.Leaf

First, let's deal with Leaf nodes. Only 2 scenarios are possible with them:

1. The rest of the path we follow is fully consistent with the path stored in the Leaf node. In this case, we just need to change the value, save the new node and return the link to it.

   
   

2. The paths are different.
   In this case, you need to create a Branch node that will separate these two paths.
   If one of the paths is empty, then its value will be transferred directly to the Branch node.
   Otherwise, we will have to create two Leaf-nodes, shortened by the length of the common part of the paths + 1 nibble (this nibble will be indicated by the index of the corresponding branch of the Branch-node).

   
   

You will also need to check if there is a common part of the path to see if we need to create an Extension node as well.

In the code, it will look like this:

 if type(node) == Node.Leaf: if node.path == path: #  .       . node.data = value return self._store_node(node) #    . #    . common_prefix = path.common_prefix(node.path) #      . path.consume(len(common_prefix)) node.path.consume(len(common_prefix)) #  Branch . branch_reference = self._create_branch_node(path, value, node.path, node.data) # ,    Extension-. if len(common_prefix) != 0: return self._store_node(Node.Extension(common_prefix, branch_reference)) else: return branch_reference 

The _create_branch_node procedure is as follows:

 def _create_branch_node(self, path_a, value_a, path_b, value_b): #    Branch-. branches = [b''] * 16 # ,     Branch- . branch_value = b'' if len(path_a) == 0: branch_value = value_a elif len(path_b) == 0: branch_value = value_b #    Leaf-,  . self._create_branch_leaf(path_a, value_a, branches) self._create_branch_leaf(path_b, value_b, branches) #  Branch-     . return self._store_node(Node.Branch(branches, branch_value)) def _create_branch_leaf(self, path, value, branches): # ,     Leaf-. if len(path) > 0: #    ( ). idx = path.at(0) #  Leaf-   ,     . leaf_ref = self._store_node(Node.Leaf(path.consume(1), value)) branches[idx] = leaf_ref 

if type(node) == Node.Extension

In the case of an Extension node, everything looks like a Leaf node.

1. If the path from the Extension node is a prefix for our path, we simply move recursively further.

   
   

2. Otherwise, we need to do the separation using the Branch node, as in the case described above.

   
   

Accordingly, the code:

 elif type(node) == Node.Extension: if path.starts_with(node.path): #         . new_reference = \ self._update(node.next_ref, path.consume(len(node.path)), value) return self._store_node(Node.Extension(node.path, new_reference)) #  Extension-. #     . common_prefix = path.common_prefix(node.path) #  . path.consume(len(common_prefix)) node.path.consume(len(common_prefix)) #  Branch- ,  ,    . branches = [b''] * 16 branch_value = value if len(path) == 0 else b'' #     Leaf-  Extension- . self._create_branch_leaf(path, value, branches) self._create_branch_extension(node.path, node.next_ref, branches) branch_reference = self._store_node(Node.Branch(branches, branch_value)) # ,    Extension-. if len(common_prefix) != 0: return self._store_node(Node.Extension(common_prefix, branch_reference)) else: return branch_reference 

The _create_branch_extension procedure _create_branch_extension logically equivalent to the _create_branch_leaf procedure, but works with the Extension node.

if type(node) == Node.Branch

But with the Branch-node, everything is simple. If the path is empty, we simply store the new value in the current Branch node. If the path is not empty - we bite one nibble from it and recursively go below.

The code, I think, does not need comments.

 elif type(node) == Node.Branch: if len(path) == 0: return self._store_node(Node.Branch(node.branches, value)) idx = path.at(0) new_reference = self._update(node.branches[idx], path.consume(1), value) node.branches[idx] = new_reference return self._store_node(node) 

delete

Fuh! The last method remains. He is the most fun. The complexity of the deletion lies in the fact that we need to return the structure to the state in which it would fall if we had done the whole chain of update , excluding only the key being deleted.

This is extremely important, since otherwise a situation is possible in which for two trees containing the same data, the root hash will differ. "", , .

. , N- , N+1 . enum — DeleteAction , .

delete :

 class MerklePatriciaTrie: # ... # Enum, ,         . class _DeleteAction(Enum): #    . #     , #        (_DeleteAction, None). DELETED = 1, #    (,    ). #     ,    #    : (_DeleteAction, ___). UPDATED = 2, #    Branch-  .   -- #    : # (_DeleteAction, (___, ___)) USELESS_BRANCH = 3 def delete(self, encoded_key): if self._root is None: return path = NibblePath(encoded_key) action, info = self._delete(self._root, path) if action == MerklePatriciaTrie._DeleteAction.DELETED: #   . self._root = None elif action == MerklePatriciaTrie._DeleteAction.UPDATED: #   . new_root = info self._root = new_root elif action == MerklePatriciaTrie._DeleteAction.USELESS_BRANCH: #   . _, new_root = info self._root = new_root def _delete(self, node_ref, path): node = self._get_node(node_ref) if type(node) == Node.Leaf: pass elif type(node) == Node.Extension: pass elif type(node) == Node.Branch: pass 

, get update . . .

if type(node) == Node.Leaf

. . — , , .

:

 if type(node) == Node.Leaf: if path == node.path: return MerklePatriciaTrie._DeleteAction.DELETED, None else: raise KeyError 

, "" — . , . .

if type(node) == Node.Extension

C Extension- :

1. , Extension- . — .
2. _delete , "" .
3. . :

• . .
• . .
• Branch-. . , Branch- . , , Leaf-. — Extension-.

:

 elif type(node) == Node.Extension: if not path.starts_with(node.path): raise KeyError #   . #       . action, info = self._delete(node.next_ref, path.consume(len(node.path))) if action == MerklePatriciaTrie._DeleteAction.DELETED: return action, None elif action == MerklePatriciaTrie._DeleteAction.UPDATED: #    ,     . child_ref = info new_ref = self._store_node(Node.Extension(node.path, child_ref)) return action, new_ref elif action == MerklePatriciaTrie._DeleteAction.USELESS_BRANCH: #     Branch-. stored_path, stored_ref = info # ,     Branch-. child = self._get_node(stored_ref) new_node = None if type(child) == Node.Leaf: #  branch-  . #     Leaf-  Extension. path = NibblePath.combine(node.path, child.path) new_node = Node.Leaf(path, child.data) elif type(child) == Node.Extension: #  Branch-  Extension-. #       . path = NibblePath.combine(node.path, child.path) new_node = Node.Extension(path, child.next_ref) elif type(child) == Node.Branch: #  Branch-      Branch-. #    Extension-    . path = NibblePath.combine(node.path, stored_path) new_node = Node.Extension(path, stored_ref) new_reference = self._store_node(new_node) return MerklePatriciaTrie._DeleteAction.UPDATED, new_reference 

if type(node) == Node.Branch

.

Almost. Branch-, …

Why? Branch- Leaf- ( ) Extension- ( ).
, . , — Leaf-. — Extension-. , , 2 — Branch- .

? :

:

1. , .
2. , _delete .

:

 elif type(node) == Node.Branch: action = None idx = None info = None if len(path) == 0 and len(node.data) == 0: raise KeyError elif len(path) == 0 and len(node.data) != 0: node.data = b'' action = MerklePatriciaTrie._DeleteAction.DELETED else: #   ,    . #    . idx = path.at(0) if len(node.branches[idx]) == 0: raise KeyError action, info = self._delete(node.branches[idx], path.consume(1)) #  ,   ,  . #      -    #    . node.branches[idx] = b'' 

_DeleteAction .

1. Branch- , ( , ). .

 if action == MerklePatriciaTrie._DeleteAction.UPDATED: #   . next_ref = info node.branches[idx] = next_ref reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.UPDATED, reference elif action == MerklePatriciaTrie._DeleteAction.USELESS_BRANCH: #    . _, next_ref = info node.branches[idx] = next_ref reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.UPDATED, reference 

1. ( , ), , .

. :

• . , , , . , .
• , . Leaf- . .
• , . , , .
• , , Branch- . , _DeleteAction — UPDATED .

 if action == MerklePatriciaTrie._DeleteAction.DELETED: non_empty_count = sum(map(lambda x: 1 if len(x) > 0 else 0, node.branches)) if non_empty_count == 0 and len(node.data) == 0: # Branch- ,  . return MerklePatriciaTrie._DeleteAction.DELETED, None elif non_empty_count == 0 and len(node.data) != 0: #  ,   . path = NibblePath([]) reference = self._store_node(Node.Leaf(path, node.data)) return MerklePatriciaTrie._DeleteAction.USELESS_BRANCH, (path, reference) elif non_empty_count == 1 and len(node.data) == 0: #  ,   . return self._build_new_node_from_last_branch(node.branches) else: #  1+   ,  2+ . # Branch-  ,   - UPDATED. reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.UPDATED, reference 

_build_new_node_from_last_branch .

— Leaf Extension, , .

— Branch, Extension , , Branch.

 def _build_new_node_from_last_branch(self, branches): #    . idx = 0 for i in range(len(branches)): if len(branches[i]) > 0: idx = i break #     . prefix_nibble = NibblePath([idx], offset=1) #     child = self._get_node(branches[idx]) path = None node = None #   . if type(child) == Node.Leaf: path = NibblePath.combine(prefix_nibble, child.path) node = Node.Leaf(path, child.data) elif type(child) == Node.Extension: path = NibblePath.combine(prefix_nibble, child.path) node = Node.Extension(path, child.next_ref) elif type(child) == Node.Branch: path = prefix_nibble node = Node.Extension(path, branches[idx]) #  . reference = self._store_node(node) return MerklePatriciaTrie._DeleteAction.USELESS_BRANCH, (path, reference) 

Rest

. , … root .

Here is:

 class MerklePatriciaTrie: # ... def root(self): return self._root 

, .

… . , , Ethereum . , , , . , :)

, , pip install -U eth_mpt — .

results

?

, -, , - , , . — , .

-, , , — . , skip list interval tree, — , , .

-, , . , - .

-, — .

, , — !

: 1 , 2 , 3 . ! , .