Types of infinity and brain removal

This article is a continuation of an article about huge numbers . But now we will go even further - at infinity of infinity.

For this we need ZFC - Zermelo set theory, Frenkel + Choice. Choice is an axiom of choice, the most controversial axiom of set theory. She deserves a separate article. It is assumed that you know what the "power" of the set is. If not, google it, for sure it is better stated than I can. Here I will just remind some

Known Facts

The power of the set of integers is denoted $\ aleph_0$ . This is the first infinite power, such sets are called countable.
The power of any infinite subset of integers is simple, even, and so on. - also countable.
The set of rational numbers, that is, the fractions p / q is also countable, they can be traversed by a snake.
For any power there is a powerset operation - the set of all subsets that creates more power than the original one. Sometimes this operation is referred to as raising a power of two, that is, $powerset (\ aleph_0) = 2 ^ {\ aleph_0} = \ aleph_c$ . The powerset of the calculated power is the power of the continuum.
The power of the continuum has: finite and infinite segments, flat and three-dimensional figures, and even n-dimensional spaces entirely
For ordinary mathematics, the next power, $powerset (\ aleph_c)$ practically not needed, usually all work happens with countable sets and sets of the power of the continuum

Now

Little known facts

In ZFC, not all collections of elements can be sets. There are so wide collections that it is impossible to allow them to be sets, paradoxes arise. In particular, the “ set of all sets ” is not a set. However, there are set theories where such sets are allowed.
')
Farther. Set theory ... What kind of objects? Numbers? Apples? Oranges? Oddly enough, ZFC does not need any objects. Take the empty set {} and agree that it means 0. 1 we denote by {{}}, two as {{{}}} and so on. {5,2} is {{{{{{}}}}}, {{{}}}}. With the help of integers we can create real numbers, and collections of real ones create any shapes.

Thus, the theory of sets is ... how to say ... hollow theory. This theory is about nothing. More precisely, about how you can nestit (nest, that is, to invest into each other) curly brackets.

The only operation that is defined in set theory is

$\ in$ - symbol of belonging. But what about the union, exception, equality, etc.? These are all macros, for example:

$(A = B) \ equiv \ forall x ((x \ in A) = (x \ in B))$

That is, translated into Russian, two sets are considered the same when testing any element for belonging to them we will get the same results.

The sets are not ordered, but this can be corrected: let the ordered pair (p, v) be {{p}, {p, v}}. Not elegant from the point of view of a programmer, but enough for a mathematician. Now the set of all param-value pairs defines a function, which is now also a set! Et voila! All mathematical analysis, which works at the level of second-order languages , since it does not speak about the existence of numbers , but the existence of functions , collapses into a first-order language!

Thus, the theory of sets is a poor theory without objects and with one relation icon, which possesses absolutely monstrous power - without any new assumptions it gives rise to formal arithmetic, real numbers, analysis, geometry and much more. This is a kind of TOE math.

Continuum Hypothesis - CH

Is there power between

$\ aleph_0$ and

$2 ^ {\ aleph_0}$ ? This problem could not be solved by Kantor, the “king of mathematicians” Hilbert highly appreciated its importance, but only later it was proved that this hypothesis cannot be either proved or disproved. It is independent of ZFC.

This means that you can create two different mathematics: one with ZFC + CH, the other ZFC + (not CH). In fact, even more than two. Suppose we reject CH, that is, we believe that between

$\ aleph_0$ and

$2 ^ {\ aleph_0}$ there is more power. How many can there be? One, two? Gödel believed that only one. But, as it turned out, the assumption that their 2, 17, 19393493 does not lead to contradictions. Any number, but not infinite!

When we encounter an unprovable assertion in formal arithmetic, for certain reasons we know that, nevertheless, this assertion, though not provable, is actually either true or false. In set theory, this does not work, we really get different mathematics. How to treat this? There are three philosophical approaches:

Formalism: why should one be surprised? We set the rules of the game in symbols, different rules - a different result. Do not look for a problem where there is none

Platonism: But how then to explain that completely different theories, such as ZFC and New Foundations, built on completely different principles, almost always produce the same result? Does this mean that there is some kind of reality behind the formulas that we are studying? Such a view was held, for example, by Gödel.

Multiverse: We can have many axioms, sometimes giving the same result, sometimes not. We must perceive the picture as a whole - if we associate color with different systems of axioms, then the colored tree of consequences is mathematics. If something is right everywhere - it is white, but there are colored branches.

Higher and higher.

In the following, we will, for simplicity, take the continuum hypothesis, that is,

$powerset (\ aleph_0) = \ aleph_1 = \ aleph_c$ - it is very convenient. In fact, we will adopt a stronger axiom, a generalized continuum hypothesis, that there is never an intermediate power between x and powerset (x). Now we are iterating the powerset and everything is simple:

$\ aleph_0 \ rightarrow \ aleph_1 \ rightarrow \ aleph_2 \ rightarrow ... \ rightarrow \ aleph_ {36463634} \ rightarrow$

How far can we go? After an infinite number of iterations, we will reach

$\ aleph_ \ omega$ - infinite in order power! By the way, its existence was not obvious to Cantor. But second! After all, the powerset function is always defined, therefore

$\ aleph_ \ omega$ can not be the last!

$\ aleph_ \ omega \ rightarrow \ aleph _ {\ omega + 1} \ rightarrow \ aleph _ {\ omega + 2} \ rightarrow ...$

To obtain

$\ aleph _ {\ omega + 3}$ You need to repeat the powerset infinity and three more times . Have you started to tear down the roof? It's only the beginning. Because again, having iterated the powerset an infinite number of times, we will get to

$\ aleph _ {\ omega + \ omega} = \ aleph _ {\ omega2}$ , after which, naturally, goes

$\ aleph _ {\ omega2 + 1}$

Reaching infinite an infinite number of times , we get the index

$\ omega ^ 2$ . How do you like this power, for example:

$\ aleph _ {\ omega ^ 3 + \ omega ^ 2 + \ omega4 + 48745}$ ? While we iterated the powerset on the list of ordinals, here are the initial ordinals:

but they are much, much more. So we’ll skip it all at once and do it.

Immediately big step

Attention! What is written further can be dangerous for your brain! We iterated the powerset counting times, and didn’t we wipe on the continuum ? Honestly, I myself am a little sausage from the fact that the cycle can run a continuum once, but set theory requires the existence

$\ aleph _ {\ aleph_1}$

Next we go faster:

$\ aleph _ {\ aleph_1} \ rightarrow \ aleph _ {\ aleph_2} ... \ rightarrow \ aleph _ {\ aleph_ \ omega} = \ aleph _ {\ aleph_ \ aleph} \ rightarrow$

The last alef index is zero, but local latex does not allow to put it - too many levels. But most importantly, you understand what new monstrous power we would create, we can say - aha, this is just a repeater , and put the whole structure to a new alef as an index. Now the power grows like a snowball, we are not stopped, the pyramid of alephs is getting higher, and we can create any power ... Or not?

Unreachable capacities

What if there is so much power

$\ theta$ that no matter how we tried to reach it “from below”, by building structures of alefs, we would not reach it? It turns out that the existence of such power, regardless of ZFC. You can accept its existence or not.

I hear the whisper "Occam's razor" ... No, no. Mathematicians adhere to the opposite principle, which is called ontological maximalism - let it exist all that is possible. But there are at least two more reasons why we would like to accept this hypothesis.

First, this is not the first unattainable power we know. The first ... is the familiar countable power. Oddly enough, it has all the properties unattainable - it's just not customary to call it that:
There is no way to get infinite power “from below” - neither adding elements a finite number of times, nor iterating a powerset () a finite number of times, using finite sets for the seed, you will not get infinity. To get infinity, you must already have it somewhere.
The existence of infinite power is introduced by a special axiom - the axiom of infinity. Without it, the existence of infinite power is unprovable.

Second: if we reject the axiom of infinity, then we get FinSet, a simple toy theory of sets with finite sets. Let's write out all these sets (the so-called model of the theory )

{}
{{}}
{{{}}, {}}
{{{{}}}}
{{{{}}}, {{}}}
{{{{}}}, {{}}}
{{{{}}}, {{}}, {}}
...

And we get ... an infinite set of finite sets ... That is, the model of the theory of finite sets is infinite, and plays the role of "the set of all sets" in it. Perhaps this will help to understand why a theory cannot speak of “the set of all sets” - such a set always exists as a model outside the theory and has different properties than the set inside. You cannot add to the theory of finite sets the infinite.

And yes,

$\ theta$ it is the “set of all sets” of the ZFC theory. In this video at the end it is very beautifully said about the unattainable power, but we have to go on.

Even further.

Of course, we can go further by iterating

$powerset (\ theta)$ . Having passed all the stages described, having built huge towers of repeaters, we again rest on the unreachable cardinal (but now we do not need new axioms, with the axiom of the existence of unattainable power, which we have just added, this has become provable). And again and again.

$\ theta_0 \ rightarrow \ theta_1 \ rightarrow \ theta_2 \ rightarrow ... \ rightarrow \ theta_ {36463634} \ rightarrow$

Notice that now the arrow makes sense not as the execution of the Powerset () function, but GetNextInaccessible (). Otherwise, everything looks very similar, we have:

$\ theta _ {\ theta_1} \ rightarrow \ theta _ {\ theta_2} ... \ rightarrow \ theta _ {\ theta_ \ omega} \ rightarrow \ theta _ {\ theta_ \ theta} \ rightarrow$

Now we will definitely achieve anything ... Or not?

The hierarchy of high power.

Yes, with GetNextInaccessible, we will push into hyper-unattainable power. Its existence requires accepting one more axiom. There are hyper-hyper-unattainable capacities. And so on. But there are other ways to determine the power , not only through unattainability:

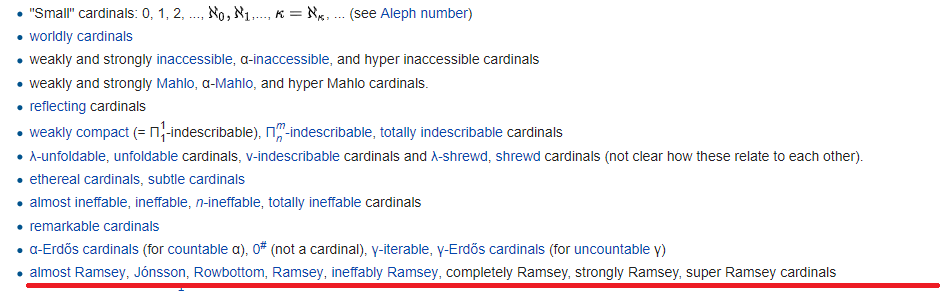
For each link there is, as a rule, a whole infinite hierarchy with an arbitrary number of hyper-prefixes and repeaters. However, the total number of formulas defining the unreachable cardinals is not that big - the number of formulas is countable !!! Therefore, sooner or later they will end. Where they end, a red line is drawn. Anything below this trait is more fragile, albeit formally.

The red line itself marks the end of Gödel’s universe (but don’t forget that Gödel created TWO different universes) - the universe of sets constructed “from below” using formulas. The powers above the red line are called hmm, “small,” and below, big:

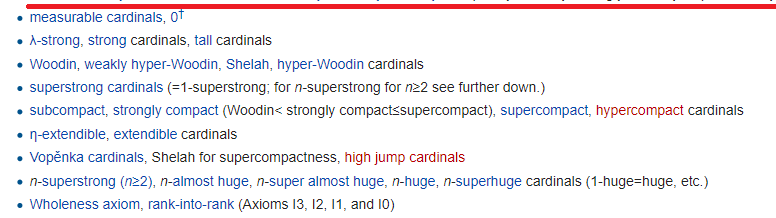
The main idea in them is that the universe of sets becomes so large that it begins to repeat itself in different ways. Each line, as always, requires a separate axiom, and several. And what is even more interesting, all this is not as useless as you might think. For example, the strongest axiom (rank-in-rank), in the lowest line, is needed to prove the fact about tablets .

Below is a poll, the last choice is decrypted here .

Source: https://habr.com/ru/post/445904/

All Articles