Ensemble methods. Excerpt from a book

Hi, Habrozhiteli, we have handed over to the printing house a new book , Machine Learning: Algorithms for Business . Here we present an excerpt about ensemble methods, its purpose is to explain what makes them effective, and also how to avoid common mistakes leading to their misuse in finance.

6.2. Three sources of error

MO models usually suffer from three errors .

1. Offset: this error is caused by unrealistic assumptions. When the offset is high, it means that the MO algorithm could not recognize the important links between the traits and the outcomes. In this situation, it is said that the algorithm is "underperformed".
')
2. Variance: this error is caused by sensitivity to small changes in the training subset. When the variance is high, this means that the algorithm is pereapodanny to the training subset, and therefore even minimal changes in the training subset can give terribly different predictions. Instead of simulating general patterns in the training subset, the algorithm mistakenly takes noise as a signal.

3. Noise: This error is caused by the variance of observed values, such as unpredictable changes or measurement errors. This is a fatal error that cannot be explained by any model.


The ensemble method is a method that combines many weak students, which are based on the same learning algorithm, with the goal of creating a (stronger) student whose performance is better than that of any of the individual students. Ensemble methods help reduce displacement and / or dispersion.

6.3. Bootstrap Aggregation

Bagging, or aggregating bootstrap samples, is an effective way to reduce variance in forecasts. It works as follows: first, it is necessary to generate N training subsets of data using random return. Second, fit the N evaluators, one for each training subset. These appraisers are adjusted independently of each other, therefore, models can be fitted in parallel. Thirdly, the ensemble forecast is a simple arithmetic average of individual forecasts from N models. In the case of categorical variables, the probability that an observation belongs to a class is determined by the proportion of appraisers who classify this observation as a member of this class (by a majority vote, that is, by a majority vote). When the baseline estimator can make predictions with a prediction probability, the bagged classifier can get an average of the probabilities.

If you use the sklearn library BaggingClassifier class to calculate out-of-package accuracy, then you should be aware of this defect: https://github.com/scikit-learn/scikitlearn/issues/8933 . One workaround is to rename the tags in integer sequential order.

6.3.1. Dispersion reduction

The main advantage of bagging is that it reduces the variance of the predictions, thereby helping to solve the problem of re-fitting. Dispersion in bagged prediction (φi [c]) is a function of the number of bagged estimators (N), the average prediction variance performed by one evaluator (σ̄), and the mean correlation between their predictions (ρ̄):


Sequential bootstrapping (Chapter 4) is to make samples as independent as possible, thereby reducing ρ̄, which should reduce the dispersion of the beggimated classifiers. In fig. 6.1 a diagram of the standard deviation of the beggy prediction is constructed as a function of N ∈ [5, 30], ρ̄ ∈ [0, 1] and σ̄ = 1.

6.3.2. Improved accuracy

Consider a bagged classifier that makes prediction on k classes by majority voting among N independent classifiers. We can denote predictions as {0,1}, where 1 means correct prediction. The accuracy of the classifier is the probability p to mark the prediction as 1. On average, we get Np predictions, marked as 1, with the variance Np (1 - p). The majority voting makes a correct prediction when the most predictable class is observed. For example, for N = 10 and k = 3, the beggimated classifier made a correct prediction when it was observed



Listing 6.1. The correctness of the bagged classifier

from scipy.misc import comb N,p,k=100,1./3,3. p_=0 for i in xrange(0,int(N/k)+1): p_+=comb(N,i)*p**i*(1-p)**(Ni) print p,1-p_ 

This is a strong argument in favor of any classifier beggling in the general case when computational capabilities permit it. However, unlike booting, beggirovanie can not improve the accuracy of weak classifiers:


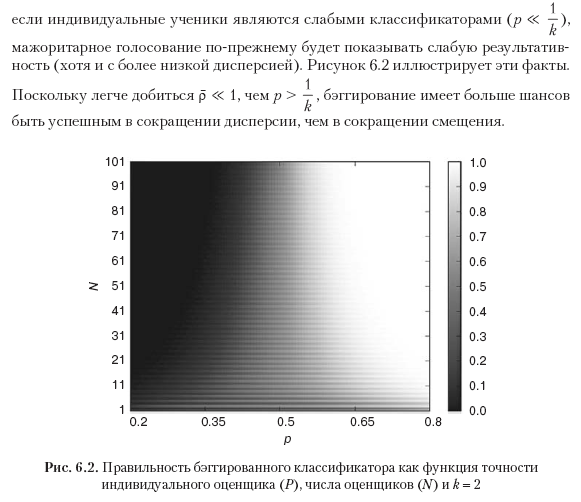
For a detailed analysis of this topic, the reader is recommended to refer to the Condorcet jury theorem. Although this theorem is obtained for the purposes of majority voting in political science, the problem addressed by this theorem has common features with the one described above.

6.3.3. Redundancy of observations

In Chapter 4, we explored one of the reasons why financial observations cannot be considered equally distributed and mutually independent. Excessive observations have two detrimental effects on bagging. First, samples taken with a refund are more likely to be almost identical, even if they do not have common observations. It makes and begging will not reduce the variance, regardless of N. For example, if each observation at t is marked in accordance with the financial return between t and t + 100, then we must select 1% of observations based on the begging valuer, but no more. In chapter 4, section 4.5, three alternative solutions are recommended, one of which was to set max_samples = out ['tW']. Mean () in the implementation of the bagged classifier class in the sklearn library. Another (better) solution was the use of the method of sequential bootstrap selection.

The second detrimental effect of redundancy in observation is that extra-packet accuracy will be inflated. This is due to the fact that random sampling with the return of samples puts samples that are very similar to those outside the package into a training subset. In this case, the correct stratified k-block cross-check without shuffling before splitting will show much lower accuracy on the test subset than the one that was evaluated outside the package. For this reason, when using this class of the sklearn library, it is recommended to set stratifiedKFold (n_splits = k, shuffle = False), cross-check the bagged classifier and ignore the out-of-packet accuracy results. A low number k is preferable to a high one, since excessive splitting will again place patterns in the test subset that are too similar to those used in the training subset.

6.4. Random forest

Decision trees are generally known for being prone to re-fitting, which increases the variance of the predictions. In order to address this problem, a random forest (RF) method was developed to generate ensemble predictions with a lower variance.

The random forest has some common similarities with the begging in the sense of training individual evaluators independently of each other on bootstrapped data subsets. The key difference from bagging is that a second level of randomness is built into random forests: during the optimization of each nodal crushing, only a random subsample (without return) of attributes will be evaluated with a view to further decorrelation of appraisers.

Like bagging, a random forest reduces the variance of forecasts without re-fitting (recall that until). The second advantage is that the random forest assesses the importance of the attributes, which we will discuss in detail in Chapter 8. The third advantage is that the random forest provides estimates of extra batch accuracy, but in financial applications they are likely to be inflated (as described in section 6.3.3). But, like begging, a random forest will not necessarily exhibit a lower offset than individual decision trees.

If a large number of samples are redundant (not equally distributed and mutually independent), a re-fitting will still take place: random selection with a return will construct a large number of almost identical trees (), where each decision tree is over-driven (a disadvantage due to which decision trees are notorious) . Unlike bagging, a random forest always sets the size of the bootstrapped samples according to the size of the training subset of data. Let's take a look at how we can solve this problem by re-fitting random scaffolding in the sklearn library. For purposes of illustration, I will refer to the classes of the sklearn library; however, these solutions can be applied to any implementation:

1. Set max_features to a smaller value in order to achieve divergence between trees.

2. Early stop: set the regularization parameter min_weight_fraction_leaf equal to a sufficiently large value (for example, 5%) so that the out-of-batch accuracy converges to non-sampling (k-block) correctness.

3. Use the BaggingClassifier estimator on the DecisionTreeClassifier base estimator, where max_samples are set equal to average uniqueness (avgU) between samples.

• clf = DecisionTreeClassifier (criterion = 'entropy', max_features = 'auto', class_weight = 'balanced')
• bc = BaggingClassifier (base_estimator = clf, n_estimators = 1000, max_samples = avgU, max_features = 1.)

4. Use the BaggingClassifier estimator on the RandomForestClassifier base estimator, where max_samples is set equal to the average uniqueness (avgU) between samples.

• clf = RandomForestClassifier (n_estimators = 1, criterion = 'entropy', bootstrap = False, class_weight = 'balanced_subsample')
• bc = BaggingClassifier (base_estimator = clf, n_estimators = 1000, max_samples = avgU, max_features = 1.)

5. Modify the class of random forest to replace standard bootstrapping with sequential bootstrapping.

In summary, Listing 6.2 demonstrates three alternative ways to customize a random forest using different classes.

Listing 6.2. Three ways to customize a random forest

 clf0=RandomForestClassifier(n_estimators=1000, class_weight='balanced_ subsample', criterion='entropy') clf1=DecisionTreeClassifier(criterion='entropy', max_features='auto', class_weight='balanced') clf1=BaggingClassifier(base_estimator=clf1, n_estimators=1000, max_samples=avgU) clf2=RandomForestClassifier(n_estimators=1, criterion='entropy', bootstrap=False, class_weight='balanced_subsample') clf2=BaggingClassifier(base_estimator=clf2, n_estimators=1000, max_samples=avgU, max_features=1.) 

When fitting decision trees, turning the attribute space in the direction coinciding with the axes, as a rule, reduces the number of levels required by the tree. For this reason, I suggest that you fit a random tree on the PCA traits, as this can speed up the calculations and slightly reduce the re-fit (more on this in Chapter 8). In addition, as described in chapter 4, section 4.8, the class_weight = 'balanced_subsample' argument will help prevent trees from properly classifying minority classes.

6.5. Boosting

Kearns and Valiant [1989] were among the first to ask whether weak appraisers could be combined in order to achieve a highly accurate appraiser. Shortly thereafter, Schapire [1990] showed an affirmative answer to this question, using the procedure we call today boosting (boosting, boost, boost). In general, it works as follows: first, generate one training subset by random selection and return in accordance with certain sample weights (initialized by uniform weights). Second, fit one evaluator using this training subset. Thirdly, if a single evaluator reaches an accuracy that exceeds the threshold of acceptability (for example, in a binary classifier, it is 50% so that the classifier works better than random fortune telling), then the evaluator remains, otherwise it is discarded. Fourth, give more weight to incorrectly classified observations and less weight to properly classified observations. Fifth, repeat the previous steps until N evaluators are received. Sixth, the ensemble forecast is the weighted average of the individual forecasts from the N models, where the weights are determined by the accuracy of the individual evaluators. There are a number of boosted algorithms, of which AdaBoost adaptive booting is one of the most popular (Geron [2017]). Figure 6.3 summarizes the decision flow in the standard implementation of the AdaBoost algorithm.

6.6. Bagging vs boosting in finance

From the above description, several aspects make booting completely different from beggirovanie :

• The fitting of individual classifiers is performed sequentially.
• Weakly effective classifiers are rejected.
• At each iteration, the observations are weighted differently.

The ensemble forecast is the weighted average of individual students.

The main advantage of booting is that it reduces both the variance and the shift in the forecasts. However, offset correction occurs at the expense of a greater risk of re-fitting. It can be argued that in financial applications, begging is generally preferable to booting. Bagging solves the problem of reconfiguration, while boosting solves the problem of undersampling. Re-fitting is often a more serious problem than under-fitting, since it is not difficult to fit the MO algorithm too tightly to financial data due to the low signal-to-noise ratio. Moreover, beggirovaniya amenable to parallelization, whereas booting usually requires sequential execution.

6.7. Bagging for scalability

As you know, some popular MO algorithms do not scale very well depending on the sample size. The support vector machine (SVM) method is a prime example. If you try to fit the SVM evaluator on a million observations, it may take a long time until the algorithm converges. And even after it has come together, there is no guarantee that the solution is a global optimum or that it will not be overtaken.

One of the practical approaches is to build a beggy algorithm, where the baseline evaluator belongs to a class that does not scale well with the sample size, for example, SVM. In determining this basic appraiser, we introduce a hard condition for an early stop. For example, in the implementation of support vector machines (SVM) in the sklearn library, you could set a low value for the max_iter parameter, for example, 1E5 iterations. The default value is max_iter = -1, which tells the evaluator to continue with the iterations until the errors fall below the tolerance level. On the other hand, you can increase the tolerance level using the tol parameter, which by default has the value tol = iE-3. Either of these two parameters will result in an early stop. You can stop other algorithms early by using equivalent parameters, such as the number of levels in a random forest (max_depth) or the minimum weighted proportion of the total weights (of all input samples) that must be on the leaf node (min_weight_fraction_leaf).

Given that the legacy algorithms can be parallelized, we transform a large sequential task into a number of smaller ones that are executed simultaneously. Of course, an early stop will increase the variance of results from individual baseline appraisers; however, this increase can be more than offset by a decrease in variance associated with the beggi ng algorithm. You can control this reduction by adding new independent baseline evaluators. Used in this way, begging will provide fast and robust estimates on very large data sets.

»More information about the book can be found on the publisher's website.
» Table of Contents
» Excerpt

For Habrozhiteley 25% discount on pre-order book coupon - Machine Learning