Muon catalysis from the point of view of quantum chemistry. Part II: electronic vs. muon chemical bond

Mnogabukaff that quantum chemistry thinks about the principle of muon catalysis: how exactly muon lowers the temperature of the desired plasma. In two parts (the first part can be read here ).

The essence of the second part is simple: the muon is heavier than the electron, so it provides a stronger chemical bond and a greater convergence of the nuclei, thereby lowering the required plasma temperature for igniting a thermonuclear reaction.

But those who want to look at formulas, graphs, and see the conceptual essence of quantum chemistry as applied to the simplest (quasi) molecules, welcome under cat.
')

Introduction

In the first part (see here ) we have disassembled the difference between a hydrogen atom $$$\ mathrm {H} ^ \ cdot = \ mathrm {p ^ + e ^ -}$ from its heavy muon counterpart $$$\ mathrm {p} ^ + \ mu ^ -$ : in the second case, the muon will be attached more strongly, and it will sit at a closer distance from the proton. At the same time, we sorted out some important things that we need here (the forms of the orbitals and the atomic system of units).

In the second part (i.e., here) we will try to understand why, how and how much the plasma temperature required for igniting a thermonuclear reaction will decrease. The reactions that interest us are of the form:

$$

$$\ mathrm {{} ^ nH + {} ^ m H \ rightarrow} \ \ text {new kernels + energy}$$

where n, m = 1,2,3 correspond to proton, deuterium and tritium, respectively. Naturally, these nuclei have a positive charge, so if you try to bring them together, they will start to repel in accordance with Coulomb's law (see the previous part ), and this is the very barrier that prevents the onset of fusion reactions. By the way, in the case of nuclear decay reactions, this repulsion has the opposite role, because after separation from the common core, the fragments, pushing away from each other, acquire additional kinetic energy, and it is this energy that heats the water at nuclear power plants.

To overcome this Coulomb barrier, an increase in plasma temperature ( T ) is required, which, as everyone remembers from the school ICT course, is related to the average particle velocity in the plasma ( v ) by the formula

$$

$$mv ^ 2 = 3k_ \ mathrm {B} T$$

where m is the mass of particles, and $$$k_ \ mathrm {B}$ - Boltzmann constant .

But let us imagine that we have combined two hydrogen nuclei into a certain particle, where they are already located closely, and therefore the rest of the barrier for them is already very small. Then we would need to significantly less accelerate these particles (read: we need lower temperatures) to combine them into something new. And precisely this role should be played by the intermediate ion. $$$(\ mathrm {{} ^ nH} \ mu ^ - \ mathrm {{} ^ mH}) ^ +$ analogue of the ion of the hydrogen molecule $$$\ mathrm {H} _2 ^ + = (\ mathrm {He ^ -H}) ^ +$ .
Having considered the differences between these two particles, we will understand how effective the muon is in lowering the ignition temperature of thermonuclear fusion.

MILK MO MOKA

So, we have our molecular system consisting of 2 hydrogen nuclei with charge + e (one electron charge in absolute value) and one particle (electron or muon) with charge - e . This system with us, while not encountering other particles, is isolated, and therefore its energy can be decomposed into its component parts:

$$

$$E = T (\ mathrm {H} _1) + T (\ mathrm {H} _2) + \ underbrace {T (\ mathrm {e} ^ - / \ mu ^ -) + V (\ mathrm {H_1 \ text {from} H_2} + V (\ mathrm {\ mathrm {e} ^ - / \ mu ^ - \ text {k} \ mathrm {H} _1}) + V (\ mathrm {\ mathrm {e} ^ - / \ mu ^ - \ text {k} \ mathrm {H} _2})} _ {E_ \ mathrm {e}}$$

where are the first two terms ( $$$T (\ mathrm {H} _1)$ and $$$T (\ mathrm {H} _2)$ ) Is the kinetic energy of hydrogen nuclei, the third member ( $$$T (\ mathrm {e} ^ - / \ mu ^ -)$ ) - the kinetic energy of a negative particle (electron or muon), the fourth member $$$V (\ mathrm {H_1 \ text {from} H_2})$ - this is the energy of the Coulomb repulsion of the hydrogens from each other, and the remaining two are the Coulomb attraction of the electron / muon to each of the protons. In the general case, this is a 3-body problem, only still quantum. Naturally, to solve it in the forehead is very difficult. But, fortunately, the nuclei are at least 1,800 times heavier than an electron, and 10 times heavier than a muon, so they will obviously move more slowly than small negative particles. Due to this, you can first solve the problem in turn: first, find the energy of motions that are not related to the movement of the nuclei, i.e. $$$E_ \ mathrm {e}$ , and then the full energy. It looks like this.

1. The arrangement of hydrogen nuclei relative to each other is chosen, and this sets the Coulomb interactions between them and with the electron / muon. Coulomb potential $$$V (R) = k \ frac {q_1q_2} {R}$ depends only on the particle charges $$$q_i$ and the distance between them, so for all isotopes of hydrogen, this value will be the same. Then the problem of the electron / muon motion in the field of these nuclei is solved. This is the task of one body.
2. These energies $$$E_ \ mathrm {e}$ are calculated for all possible locations of nuclei relative to each other, and this will be the effective potential energy of the motion of the nuclei. In our case, we need to calculate the energy at different distances relative to each other, so the potential for a pair of nuclei is always one-dimensional. Well, then we only need to solve the problem of two bodies about the movement of two hydrogen isotopes relative to each other.

Obviously, we have the root of the problem in calculating the electron / muon energy in the field of nuclei $$$E_ \ mathrm {e}$ . In essence, this is a chemical bond: a kind of potential that keeps the nuclei together in certain places. And it is precisely this task of searching for the energy of chemical bonds that is the main one in quantum chemistry.

Unfortunately, both muon and electron are quantum particles, therefore, in order to find this energy, we will have to resort to methods of quantum mechanics. In fact, our electron / muon motion problem in the field of two identical nuclei is solved explicitly (see here ), but this solution is very complicated and the result is not as clear as in the case of a hydrogen-like atom. Therefore, we will try to disassemble another, approximate approach that is applicable to any systems. This is the so-called. molecular orbitals method as linear combinations of atomic orbitals, or MO LCAO.

Let's take a closer look at the Schrödinger equation for the motion of an electron / muon in the field of hydrogen nuclei:

$$

$$\ hat {H} \ psi = \ underbrace {\ left (\ overbrace {- \ frac {1} {2m} (\ frac {\ partial ^ 2} {\ partial x ^ 2} + \ frac {\ partial ^ 2} {\ partial y ^ 2} + \ frac {\ partial ^ 2} {\ partial z ^ 2})} ^ {\ hat {T}} + \ overbrace {- \ frac {1} {R_1}} ^ {\ hat {V} _1} + \ overbrace {- \ frac {1} {R_2}} ^ {\ hat {V} _2} + \ overbrace {\ frac {1} {R}} ^ {\ hat {V } _ \ mathrm {HH}} \ right)} _ {\ hat {H}} \ psi = E \ psi$$

This equation is written in the atomic system of units (see PS in the previous part ), so the nuclear charge of hydrogen and electron / muon is, respectively, +1, --1, the electron mass is m = 1, and for muon m ≈207.

And if you look closely, you can see that in the Hamiltonian you can select a piece associated purely with the movement of the negative particle around only one of the nuclei, which is simply the Hamiltonian of the hydrogen atom, and this can be done in two ways:

$$

$$\ hat {H} = (\ overbrace {\ hat {T} + \ hat {V} _1} ^ {\ hat {H} _ {1}} + \ hat {V} _2 + \ hat {V} _ \ mathrm {HH}) = (\ overbrace {\ hat {T} + \ hat {V} _2} ^ {\ hat {H} _ {2}} + \ hat {V} _1 + \ hat {V} _ \ mathrm {HH})$$

Beyond the hydrogen-like Hamiltonian of an atom ( $$$\ hat {H} _i, \ i = 1,2$ ) we always have 2 pieces: the interaction energy of an electron / muon with another nucleus ( $$$\ hat {V} _j$ ) and nuclear repulsion energy ( $$$\ hat {V} _ \ mathrm {HH}$ ). The second of them does not affect the movement of electrons at all - it is just a shift of energy by a certain amount, but the interaction of an electron with another nucleus is an important thing.
We can imagine that our particle at each moment revolves only around one of the nuclei, and the interaction with the second is just a kind of correction. As a method of rotation around one of the nuclei, we can assume that the electron / muon is in the ground (1s) state, the wave function for which we are well known from the previous part:

$$

$$| 1s \ rangle = \ frac {1} {\ sqrt {\ pi}} \ exp \ left (- \ frac {R} {R_1} \ right)$$

Where $$$R_1$ Is the Bohr radius for a particle. In the case of an electron $$$R_1 = 1$ Bohr (which is the Bohr radius for an electron, equal to about 0.5 angstroms), and in the case of a muon $$$R_1 = \ frac {1} {m_ \ mu} \ approx \ frac {1} {207}$ .
In order to somehow approximate the electron / muon wave function in a field of 2 nuclei, we can try to take the following representation:

$$

$$\ psi \ approx c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle$$

and then the problem of solving a complex partial differential equation is reduced to finding 2 unknown coefficients c ₁ and c ₂ . This is the same molecular orbital, represented as a sum with coefficients (linear combination in a scientific way) of atomic 1s orbitals.

Naturally, we need an equation for these parameters. And to get it is quite simple, if we substitute this approximation into the Schrödinger equation $$$\ hat {H} \ psi = E \ psi$ :

$$

$$\ hat {H} (c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle) = c_1 \ hat {H} | 1s_1 \ rangle + c_2 \ hat {H} | 1s_2 \ rangle = E (c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle) = c_1 E | 1s_1 \ rangle + c_2 E | 1s_2 \ rangle$$

Actually, we want this ratio to be fulfilled everywhere, so we can count the average values ​​of all this. We multiply in turn on the left this equation by $$$<1s_1 |$ and $$$<1s_2 |$ and integrate over all coordinates. As a result, we obtain a system of 2 linear equations, where we need to find the coefficients c ₁ , c ₂ and the energy E :

$$

$$\ begin {pmatrix} \ langle 1s_1 | \ hat {H} | 1s_1 \ rangle & \ langle 1s_1 | \ hat {H} | 1s_2 \ rangle \\ langle 1s_2 | \ hat {H} | 1s_1 \ rangle & \ langle 1s_2 | \ hat {H} | 1s_2 \ rangle \\ \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix} = E \ begin {pmatrix} \ langle 1s_1 | 1s_1 \ rangle & \ langle 1s_1 | 1s_2 \ rangle \\ \ langle 1s_2 | 1s_1 \ rangle & \ langle 1s_2 | 1s_2 \ rangle \\ \ end {pmatrix} \ begin {pmatrix} _1 \\ s_2 \ end {pmatrix}$$

Anyone who has studied linear algebra will know the generalized eigenvector-eigenvalue problem. Before we solve it, let us examine what the elements of the 2 matrices that exist here are equal to (and at the same time we introduce their short designation with one letter).

• Let's start with the simplest: $$$\ langle 1s_1 | 1s_1 \ rangle = \ langle 1s_2 | 1s_2 \ rangle = 1$ - this is the normalization of the wave functions, and as we remember, the total probability of finding an electron / muon is at least somewhere equal to 1.
• $$$\ langle 1s_1 | 1s_2 \ rangle = \ langle 1s_2 | 1s_1 \ rangle = S$ - this is so-called. overlap integral, showing how 1s overlap the electron clouds of each of the atoms.
• $$$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ langle 1s_2 | \ hat {H} | 1s_2 \ rangle = \ alpha$ . This integral consists of several parts:
  

  $$

  $$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ langle 1s_1 | \ hat {H} _1 | 1s_1 \ rangle} _ {- \ frac {m} {2}} + \ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle + \ frac {1} {R}$$
  
  
• $$$\ langle 1s_1 | \ hat {H} | 1s_2 \ rangle = \ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ beta$ . Here is similar:
  

  $$

  $$\ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ langle 1s_2 | \ overbrace {\ hat {H} _1 | 1s_1 \ rangle} ^ {- \ frac {m} {2} | 1s_1 \ rangle} _ _ - {\ frac {m} {2} S} + \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle + \ frac {S} {R}$$
  
  those. the energy of a hydrogen-like atom and the internuclear repulsion scaled to the overlap integral (first and last members), and the electron / muon hop energy from one atom to another.
  

Let us find the expressions for the energies of our hydrogen-like ion from the equation, rewritten as

$$

$$\ begin {pmatrix} \ alpha & \ beta \\ \ beta & \ alpha \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix} = E \ begin {pmatrix} 1 & S \\ S & 1 \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix}$$

To find the energy you need to solve the equation:

$$

$$\ det \ begin {pmatrix} \ alpha -E & \ beta -ES \\ \ beta - ES & \ alpha -E \ end {pmatrix} = (\ alpha -E) ^ 2 - (\ beta - ES) ^ 2 = 0$$

where "det" denotes a determinant (determinant of the matrix, in Russian).

The solutions of this quadratic equation for E are:

$$

$$E_ \ pm = \ frac {\ alpha \ pm \ beta} {1 \ pm S} = - \ frac {m} {2} + \ frac {1} {R} + \ frac {\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {1 \ pm S}$$

The first piece is, obviously, the energy of the atom, the second is the internuclear repulsion, that same Coulomb barrier that prevents the fusion of the thermonuclear reaction, and the last complex structure must be dealt with.

If we discard the internuclear repulsion, which is merely a reference point for the electron / muon energy, we will get that we have two states with energy

$$

$$\ epsilon_ \ pm = - \ frac {m} {2} + \ frac {\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {1 \ pm S}$$

Since both wave functions $$$| 1s_1 \ rangle$ and $$$| 1s_2 \ rangle$ - positive, and $$$\ hat {V} _i <0$ (because the negative particle always pulls towards the positive), then $$$\ epsilon_ + <- \ frac {m} {2}$ (energy of a single atom), and $$$\ epsilon_-> - \ frac {m} {2}$ i.e. we get a standard picture of molecular orbitals:



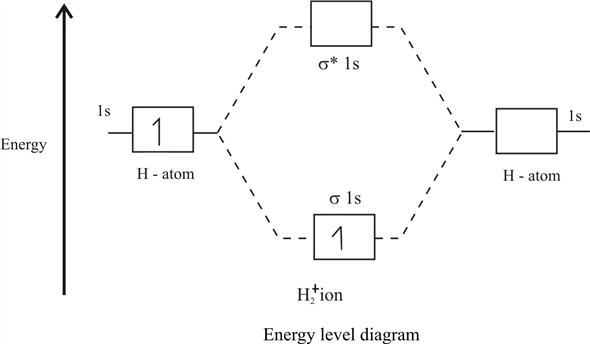
Lower orbital with energy $$$E _ +$ called binding, and the top (with energy $$$E _-$ ) - anti-binding, or loosening. As a result, if the electron / muon sits on the lower molecular orbitals, then it benefits from flying around 2 nuclei than around one, and by its movement it lowers the total energy of the system. And this is the very magical chemical bond that screens off the internuclear repulsion, allowing the nuclei to be next to each other for quite a long time.

And here we have to calculate the integrals of chemical bonding in order to understand how closely the nuclei of hydrogen are allowed. In fact, all three required integrals are calculated analytically, but it is terribly hemorrhoidal and difficult (for whom it is interesting, see Chapter 9 in the book “Quantum Chemistry” by Flarry ). Therefore, we will go another way, more simple, and calculate these integrals numerically using the Monte Carlo method.

Metropolis Method

It seems to me very logical, in the text on thermonuclear energy to pay homage to her grandfather: a military atom, and more specifically, a Manhattan project . It was from him that the Monte-Carlo method, and in particular the Metropolis algorithm , grew out of which, one of the authors, Edward Teller, is the “father of the hydrogen bomb” (that is, the person who launched thermonuclear fusion on the Enolvetok atoll).


In general, we analyze the essence of the method. It is intended for problems of statistical mechanics. The main distribution in it is the Boltzmann distribution: the probability to detect a system in a certain state is equal to $$$\ exp (- \ beta E)$ , $$$\ beta ^ {- 1} = k_ \ mathrm {B} T$ . And the observed value of some parameter A for a system in thermodynamic equilibrium is equal to the integral

$$

$$\ langle A \ rangle = \ frac {1} {Z} \ int A (q) \ exp (- \ beta E (q)) dq$$

where q is the coordinates that parameterize the state of the system (for example, the coordinates / momenta of the particles), and Z is the normalization factor, called the partition function:

$$

$$Z = \ int \ exp (- \ beta E (q)) dq$$

If there are soooo many particles in the system, then it is completely unrealistic to count any of the integrals over the forehead. The naive Monte Carlo method, in which we simply choose a bunch of random values ​​of the coordinates q, also does not give anything efficient, if there are really possible system states for which the probability $$$\ exp (- \ beta E)$ noticeably non-zero, very little. And it is for such cases that a sample of significance is needed, in which we will allow the algorithm to sample only sufficiently probable places in the state space.

Metropolis algorithm looks like this.

1. At the initiation of the simulation, we choose some starting approximation in the configuration space $$$\ mathbf {q} ^ {(0)}$ and some vector of the highest possible increment $$$\ delta \ mathbf {q}$ . At the starting point, we calculate the energy of the system $$$E ^ {(0)} = E (\ mathbf {q} ^ {(0)})$ (read - probability $$$p = \ exp (- \ beta E ^ {(0)})$ ).
2. The new configuration on the nth step is as follows.
   
   1. We calculate the energy of the test configuration $$$E_ \ mathrm {trial} = E (\ mathbf {q} _ \ mathrm {trial})$ (i.e. probability $$$p_ \ mathrm {trial} = \ exp (- \ beta E_ \ mathrm {trial})$ ).
   2. And then compare with each other the old probability $$$p ^ {(n)}$ with trial $$$p_ \ mathrm {trial}$
      
      
      • if the new configuration has a greater or equal probability ( $$$\ frac {p_ \ mathrm {trial}} {p ^ {(n)} \ geq 1$ ), or, equivalently, the energy of the new point is lower or the same as in the old one ( $$$E_ \ mathrm {trial} \ leq E ^ {(n)}$ ), then a new point is accepted and the system goes into it ( $$$q ^ {(n + 1)} = q_ \ mathrm {trial}$ ),
      • if the trial configuration is higher in energy ( $$$E_ \ mathrm {trial}> E ^ {(n)}$ ) equivalent to $$$\ frac {p_ \ mathrm {trial}} {p ^ {(n)}} <1$ then in this case we generate a random number $$$P \ in [0; 1)$ from a uniform distribution, and compare it with the ratio of probabilities, which are the transition probability. If a $$$P <\ frac {p_ \ mathrm {trial}} {p ^ {(n)}}$ , then we accept a new point, and if not ( $$$P \ geq \ frac {p_ \ mathrm {trial}} {p ^ {(n)}}$ ), then reject, and the system remains in the old configuration ( $$$q ^ {(n + 1)} = q ^ {(n)}$ ) ...
      
      
   
   
3. Taking many steps according to the algorithm above, we sample a significant (that is, really important) part of the possible system configuration space. The integral we are interested in is calculated by the formula:
   $$$\ langle A \ rangle = \ frac {1} {Z} \ int A (\ mathbf {q}) \ exp (- \ beta E (\ mathbf {q})) d \ mathbf {q} = \ frac { 1} {N} \ sum_ {n = 0} ^ {N} A (\ mathbf {q} ^ {(n)})$
   

This is how the Metropolis algorithm works.

And now we need to adapt it to the calculation of the 3 integrals of interest to us. Let's look at them in more detail.

• $$$S (R) = \ langle 1s_2 | 1s_1 \ rangle = \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-m \ underbrace {| \ mathbf {r} - \ mathbf {r} _2 | } _ {R_2})} _ {1s_2}} ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-m \ underbrace {| \ mathbf {r} - \ mathbf {r} _1 |} _ {R_1})} _ {1s_1}} ^ {p (\ mathbf {r})} dx dy dz$ where $$$\ mathbf {r} = (x, y, z) ^ \ mathbf {T}$ - coordinates of the electron / muon, $$$\ mathbf {r} _i = (x_i, y_i, z_i) ^ \ mathbf {T}$ - coordinates of hydrogen nuclei, and $$$R_i = | \ mathbf {r} - \ mathbf {r} _i | = \ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2 + (z-z_i) ^ 2}$ - the distance between positive and negative particles,
  
• $$$\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle = - \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1} \ frac {1} {R_2} } ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1}} ^ {p (\ mathbf {r})} dxdydz$
• $$$\ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle = - \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_2)} _ {1s_2} \ frac {1} {R_1} } ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1}} ^ {p (\ mathbf {r})} dxdydz$

It can be seen that if we count the 1s-function of one of the atoms for the probability p ,


then everything else under the integral sign (the second wave function and in 2 out of 3 cases the potential of attraction of an electron / muon to the nucleus) will be a function whose average value is calculated.The only thing that has to be done, in contrast to the usual calculation using the Metropolis method, is to correct the normalization of the integrals. The fact is that the standard normalization will be

$$

$$Z=\int \limits_{-\infty}^{+\infty} \int \limits_{-\infty}^{+\infty} \int \limits_{-\infty}^{+\infty} \exp(-m R) dx dy dz = 4 \pi \int \limits_{0}^{+\infty} \exp(-m R) R^2 dR = \frac{8 \pi}{m^3}$$

And we need a normalization on $$$\sqrt{\langle 1s_1 | 1s_1 \rangle}$ where

$$

$$\langle 1s_1 | 1s_1 \rangle = \int \limits_{-\infty}^{+\infty} \int \limits_{-\infty}^{+\infty} \int \limits_{-\infty}^{+\infty} \exp(-2 m R) dx dy dz = 4 \pi \int \limits_{0}^{+\infty} \exp(-2m R) R^2 dR = \frac{\pi}{m^3}$$

This means that each integral calculated by Metropolis will need to be multiplied by a factor

$$

$$\frac{Z}{\sqrt{\langle 1s_1 | 1s_1 \rangle} } = 8 \sqrt{\frac{\pi}{m^3}}$$

This can already be organized in the form of a certain script, for example, in Python (here is an example of code).


Using such calculations, we can finally compare the potential energies in the hydrogen ion $$$\ mathrm {H} _2 ^ +$ and its muon counterpart.

$$$\ mathrm {H_2 ^ + = p ^ + e ^ - p ^ +}$ vs. $$$\ mathrm {p ^ + \ mu ^ - p ^ +}$

So, armed with a script, we can calculate the surface potential energy of the convergence of hydrogen nuclei connected by an electron and a muon. As the reference point of energy we take the atoms infinitely divorced from each other (i.e. $$$-m / 2$ which is equal to the potential when the distance between the cores $$$R = + \ infty$ ).

In the case of an electron, the potential near the minimum looks like this:



The minimum occurs at a distance of about 2 Bohr (ie, approximately the sum of 2 atomic radii), and the dissociation energy of the molecule into fragments is approximately 0.06 Hartree, which corresponds to heating to about 20,000 Kelvin (or Celsius, it does not matter). To convert energies, I recommend using online resources like this .

The situation is similar with the muon-bound hydrogen ion:



Since the Bohr radius for muon hydrogen is less (see the previous part ), the hydrogen nuclei in the minimum of potential energy sit about 200 times closer. The energy of the gap of this molecule is already more than 10 Hartree, which corresponds to a temperature of more than three degrees Lyamov ( $$$\ approx (3.2 \ cdot 10 ^ 6) ^ \ circ$ ).

For ignition, the reaction usually requires a temperature of about 10 ⁸ K , which is about 320 Hartree. Let us see at what distances such energy is achieved in the case of the usual divodor ion and in the case of its muon version:



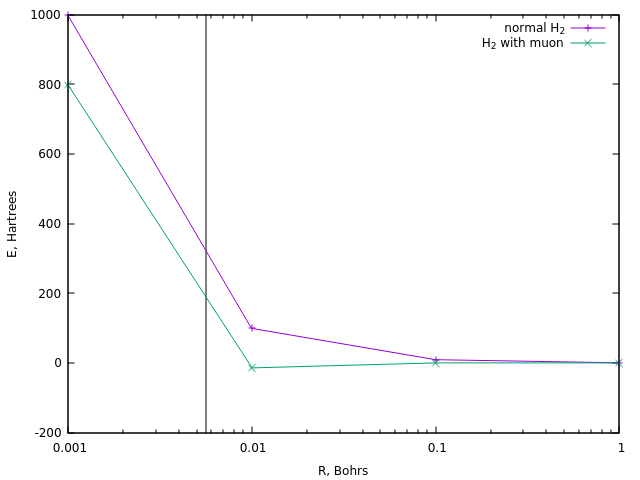
In the case of the first, this corresponds to a distance of about 0.0058 Bor (vertical line).

The same distance in muon hydrogen is reached at an energy of about 190 Xa, i.e. about half as much. And this is the simplest estimate of the temperature of muon catalysis.

But in fact, everything will be even steeper. The fact is that if you form a stable particle $$$\ mathrm {({} ^ mH (\ mu ^ -) {} ^ nH) ^ +}$ then these nuclei, while the muon is alive, will fluctuate relative to each other. And here tunneling from the state of “two hydrogen atoms” to the state of “heavier nucleus” can occur, and the probability of tunneling depends on the required tunneling length d approximately like $$$p ^ {- d}$ , so that by bringing together two nuclei with a muon, we ooooofigenically greatly increase the probability of the tunneling process of this reaction. Unfortunately, evaluations of this effect no longer require quantum chemistry, but nuclear nuclear physics, so this part of the review goes beyond the scope of this post. So we will stop at this.

PS Why is not everything so simple?

In fact, it is not so easy to form these particles under plasma conditions. The fact is that if we collide two particles, then their total energy obviously exceeds the dissociation energy (or ionization, in the case of the nucleus + electron / muon), so when they collide, they do not form a stable particle (atom, ion, molecule), and past each other. In order to stick to each other, they need to throw off excess energy somewhere, and for this they need a third person who will take on this energy. This may be a photon, or some kind of left particle flying nearby, but most importantly the conditions should contribute to this carry away of excess energy.

Pps

If you have any comments / clarifications / questions, write in the comments or in lichku. I'll fix everything, answer everything and explain.