Introduction

How to find out that a person understood what monads are? He will tell you about this in the first 5 minutes of communication and will definitely try to explain. And he will also write a text about it and, if possible, publish it somewhere, so that everyone else also understands what monads are.

Among functional programmers, especially in Haskell, monads have become something of a local meme. They are often tried to be explained, starting from particular cases and immediately giving examples of use. Because of this, the listener may not catch the basic essence of the concept, and the monads will remain black magic, well, or just a means of cochilating the side effects in purely functional languages.

I will first talk about the basic concepts of category theory, and then from a practical point of view, we will approach the definition of a monad and see that in fact many programmers use this powerful abstraction in one of its manifestations.

My presentation is largely based on the book Theory of Categories for Programmers by Bartosh Milevski, which was created as a series of blog posts , is available in PDF , and recently published in paper.

Examples are given in Haskell, it is assumed that the reader is familiar with the syntax and basic concepts of the language. In the mentioned book there are examples in C ++, you can compare the purity and clarity of the code.

Categories

Definition

The categories themselves are very simple constructs. A category is a collection of objects and morphisms between them. Morphisms can be considered as unidirectional arrows connecting objects. In general, nothing is known about the essence of the objects themselves. Category theory does not work with objects, but with morphisms, more precisely, with their composition .

The following notation is used:

• Ob _C - objects of category C ;
• Hom _C (A, B) - morphisms from A to B;
• g ∘ f is the composition of the morphisms f and g.

In the definition of a category, additional restrictions are imposed on morphisms:

1. For a pair of morphisms f and g, if f is a morphism from A to B (f ∈ Hom (A, B)), g is a morphism from B to C (g ∈ Hom (B, C)), then there exists their composition g f is a morphism from A to C (g ∘ f ∈ Hom (A, C)).
2. For each object, the identical morphism id _A ∈ Hom (A, A) is given.

There are two important properties that any category must satisfy (axioms of category theory):

1. Associativity of the composition: h ∘ (g ∘ f) = (h ∘ g) f;
2. Composition with the identical morphism: if f ∈ Hom (A, B), then f ∘ id _A = id _B ∘ f = f.

Categories are very easily and naturally rendered as directed graphs. In principle, any directed graph can be added to a category by adding compositions of morphisms and identical morphisms, if necessary.

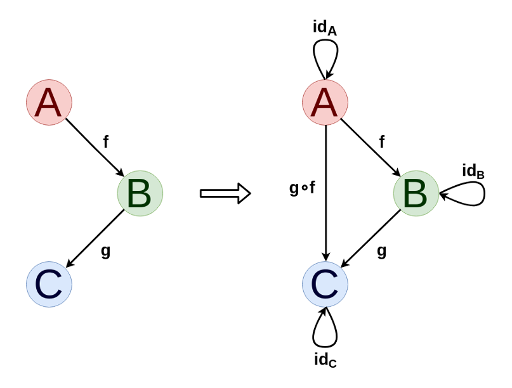
For any category, you can define a dual category (denoted by C ^op , in which morphisms are obtained by turning the arrows of the original category, and the objects are the same. This allows us to formulate dual statements and theorems, the truth of which does not change when the arrows turn.

Objects and morphisms do not necessarily form sets (in the classical sense from the theory of sets), therefore in the general case the phrase "class of objects" is used. Categories in which classes of objects and morphisms are still sets are called small categories . Further we will work only with them.

Types and functions

, Haskell, — . , Int Bool — , Int -> Bool — .

id, :

id :: a -> a
id x = x

— , Haskell :

f :: a -> b
g :: b -> c
g . f :: a -> c
(g . f) x = g (f x)

, , — , Set. , — , : . bottom, _|_. , , , bottom. Haskell, , Hask. , Set. , , : Hom_C(A, B) ∈ C. , a -> b — Haskell.

.

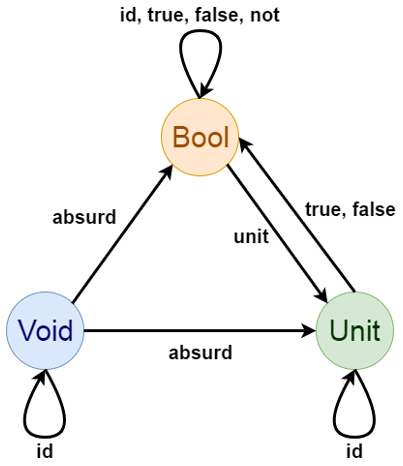
Void, ( ). absurd, , , Void, :

absurd :: Void -> a

Unit, — , (). unit , :

unit :: a -> Unit
unit _ = ()

— Bool:

data Bool = True | False

, Void, Unit Bool.

Void , absurd, Bool, Unit. , Void, , .

Bool -> Unit , unit, . Unit -> Bool . (), True, False. , Unit Bool:

true, false :: a -> Bool
true _ = True
false _ = False

Bool Bool — , 4 ( n — 2²ⁿ): id, true false, , not:

not :: Bool -> Bool
not True = False
not False = True

, :

Haskell- .

— . , C D, F . -, C D. a — C, F a — D, . -, : f :: a -> b C F f :: F a -> F b D.

, " " :

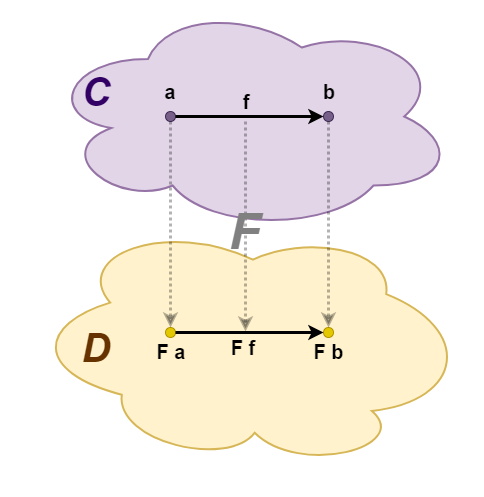
1. h = g ∘ f, F h = F g ∘ F f.
2. id_a — a, F id_a = id_{F a} — F a.

, "" : , , . , , () . , .

. , F :: C -> D G :: D -> E G . F :: C -> E. , , , , . Id_C, Id_D Id_E. , , .

, , -, — (). , Cat ( ).

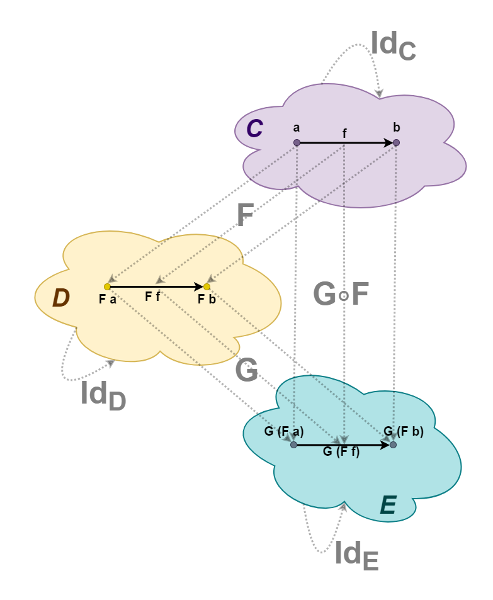
Haskell . , , - , .

Maybe , a Maybe a ( Maybe !):

data Maybe a = Nothing | Just a

, f :: a -> b F f :: Maybe a -> Maybe b. fmap. , ( ):

--          f                F f
--      /------\    /------------------\
fmap :: (a -> b) -> (Maybe a -> Maybe b)
fmap _ Nothing = Nothing
fmap f (Just x) = Just (f x)

, Maybe — . , , Functor. fmap, , ( — ):

class Functor f where
  fmap :: (a -> b) -> f a -> f b

— , , fmap . f a -> f b, , .

, , , .. , . : , - .

. , . , , — Haskell.

: upCase, , toWords, . toUpper words:

upCase :: String -> String
upCase = map toUpper

toWords :: String -> [String]
toWords = words

:

processString :: String -> [String]
processString = toWords . upCase

, . , processString "upCase toWords".

— , . -, , , -, , .

, a , .

newtype Writer a = Writer (a, String)

, Writer — , fmap:

instance Functor Writer where
  fmap f (Writer (x, s)) = Writer (f x, s)

upCase toWords , , "" Writer:

upCase :: String -> Writer String
upCase s = Writer (map toUpper s, "upCase ")

toWords :: String -> Writer [String]
toWords s = Writer (words s, "toWords ")

, , - . , b , , c c , :

compose :: (a -> Writer b) -> (b -> Writer c) -> (a -> Writer c)
compose f g = \x -> let Writer (y, s1) = f x
                        Writer (z, s2) = g y
                    in Writer (z, s1 ++ s2)

processString :

processString :: String -> [String]
processString = compose upCase toWords

. () a -> b a -> Writer b , a b. , .. a -> Writer a:

writerId :: a -> Writer a
writerId x = Writer (x, "")

, , Hask. , a b a -> b, a -> m b, .. "" - m. (embellished). m, Writer — .

C m. K, , C, .. Ob_K = Ob_C. a -> b K a -> m b C: Hom_K(a, b) = Hom_C(a, m b). , , K — C.

, , , . , m — . Haskell ( Hask):

class Monad m where
  --    
  (>=>)  :: (a -> m b) -> (b -> m c) -> (a -> m c)
  --  
  return :: a -> m a

>=>, "fish", : . , , — , , , . Writer — , compose — >=>, writerId — return.

>=> . , -. a, f, , , bind:

f >=> g = \a -> let mb = f a
                in (bind mb g)
  where
    bind :: m b -> (b -> m c) -> m c

bind b " " m , b m c. >=>. : m b -> (b -> m c) -> m c. , . "" Haskell >>=, bind, return:

class Monad m where
  (>>=)  :: m a -> (a -> m b) -> m b
  return :: a -> m a

, - b -> m c b, m b. , m, fmap, (a -> m b) -> m a -> m (m b). >>= m (m b) m b, "" , . join:

ma >>= g = join (fmap g ma)
  where
    join :: m (m a) -> m a

, Writer :

join :: Writer (Writer a) -> Writer a
join (Writer ((Writer (x, s2)), s1)) = Writer (x, s1 ++ s2)

Monad:

class Functor m => Monad m where
  join   :: m (m a) -> m a
  return :: a -> m a

, m . , fmap >>=:

fmap :: (a -> b) -> m a -> m b
fmap f ma = ma >>= (\a -> return (f a))

, "" .

(.. , ) .

(a -> [b]) -> (b -> [c]) -> (a -> [c]). :

(>=>) :: (a -> [b]) -> (b -> [c]) -> (a -> [c])
f >=> g = \x -> concat (map g (f x))

. a, , — f [b]. , b — g : map g (f x) :: [[c]]. , .

>>= :

(>>=) :: [a] -> (a -> [b]) -> [b]
xs >>= f = concat (map f xs)

return :: a -> [a]. :

return :: a -> [a]
return x = [x]

Monad:

instance Monad [] where
  xs >>= f = concat (map f xs)
  return x = [x]

, . , , . , — , ..

, , - .

, , Maybe. Just, — Nothing. , , :

(>=>) :: (a -> Maybe b) -> (b -> Maybe c) -> (a -> Maybe c)
f >=> g = \x -> case f x of
                  Just y  -> g y
                  Nothing -> Nothing

Monad Maybe:

instance Monad Maybe where
  (Just x) >>= f = f x
  Nothing  >>= f = Nothing
  return x = Just x

, . , - , , - . Either String a, : , . :

data Either a b = Left a | Right b

, . . :

type WithException a = Either String a

Maybe:

(>=>) :: (a -> WithException b) -> (b -> WithException c) -> (a -> WithException c)
f >=> g = \x -> case f x of
                  Right y -> g y
                  err     -> err

Monad :

instance Monad WithException where
  (Right x) >>= f = f x
  err >>= f = err
  return x = Right x

, , write-only , . a -> b , , . , , ( , ):

a -> s -> (b, s)

:

newtype State s a = State (s -> (a, s))

s , State s . runState:

runState :: State s a -> s -> (a, s)
runState (State f) s = f s

Functor:

instance Functor (State s) where
  fmap f state = State st'
    where
     st' prevState = let (a, newState) = runState state prevState
                     in (f a, newState)

, a b, , a -> State s b, State s — . , :

(>=>) :: (a -> State s b) -> (b -> State s c) -> (a -> State s c)
f >=> g = \x -> State (\s -> let (y, s') = runState (f x) s
                             in runState (g y) s')

Monad. , return, , -:

instance Monad (State s) where
  stateA >>= f = State (\s -> let (a, s') = runState stateA s
                              in runState (f a) s')
  return a = State (\s -> (a, s))

, . , Unit s , Unit -> State s s:

get :: Unit -> State s s
get _ = State (\s -> (s, s))

, Unit . , .

, , . , , , s Unit, s -> State s Unit:

put :: s -> State s Unit
put s = State (\_ -> ((), s))

, , /. , " " RealWorld, . RealWorld - , (, ). :

type IO a = State RealWorld a

IO — , Haskell, "". , . , , , -, .