Googleology (this is not a typo) for programmers
It is more difficult to write about mathematics (so that it was interesting) than about physics. However, I hope that you will finish reading at least up to examples of crazy programs in C.

From completely harmless things can grow monsters. Take, for example, the game in substrings. Write a string of letters a and b and select the substrings from character 1 to character 2, from 2 to 4, from three to 6, from n to 2n, while the length of the main string is enough. Our task is to ensure that in these shifts the shorter one does not enter into any longer one. I even wrote a SQL analyzer:
Here is an example of the output:
')
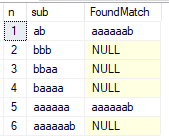
As you can see, substrings 1 and 5 did not pass the test. We can remove the last character, and the resulting string of 11 characters 'abbbaaaaaaa' will pass the check. It turns out that this is the longest possible string in the two-character alphabet that satisfies this condition.
For a single-character alphabet, the maximum string length is 3, and then for purely technical reasons. It turns out that the maximum length is finite for an alphabet of any number of letters. So, we have:
Check your intuition, how long a string can be made in an alphabet of three letters. 100? 1000? In fact, a lot more than Googol, and a lot more than GoogolPleh.
And I have to take the time to show the power of the shooters.
We use multiplication to not write a lot of addition operations:
With the help of arrows, only the smallest of the big numbers are created, if I may say so. The growth rate of functions is measured by some scale - by comparison with fast-growing functions . The first function in this hierarchy corresponds to addition, the second to multiplication, the third to the arrow, the n-ny to the n-2 arrows (approximately, not exactly). But you can define
You can go even further: fw,fw+1,fw+n,fw2,fw2,fww,fwww,f epsilon These functions are indexed by ordinals, or in Russian literature by ordinal numbers. The picture with the structure of the initial ordinal numbers is preceded by an article, but they extend much further, and further begins
The endless pyramid of 'omeg' gives some kind of ordinal e p s i l o n 0 . Read about the function , the growth of which is measured by this ordinal. It turns out that a function grows so fast that formal arithmetic cannot, in principle, prove that such a function is defined at all!
Of course, you know about the Gödel theorem that there are unprovable assertions. But, as a rule, the only example of such a statement is the very construction of Gödel (“I am unprovable”). The Goodstein theorem is a good example of this.
Moreover, it turns out that the ordinals somehow measure the power of theories . The 'strength' of formal arithmetic is equal to e p s i l o n 0 , the simplified Kripke-Platek set theory has the power of the Feferman-Schutte ordinal, and so on.
A competition was held to generate large numbers. No, programming for the Turing machine is still too cruel, so the C language was used for an abstract infinite machine with sizeof (int) = infinity. You could also use malloc (), and the amount of memory, like the stack, is unlimited. Only the length of the program was limited - the program had to fit in 512 bytes (excluding spaces), but the use of a preprocessor was allowed (#define).
The results are published on the website of mathematics . At the same time check out the design of the site of this mathematics. The results are here . Here is the text of the program that has taken the second place, giving the number about
The text of the winner’s program is longer, I just wanted to show how it begins:
But even the organizer of the competition (written very big ) found it difficult to estimate how large the number turned out.
Okay, stop doing tiny numbers, let's do big ones. Imagine that a universal contest is organized to write a program for generating the largest number. Since the number of programs is not longer than 512 characters, of course, there is an absolute winner. Let's designate it as BB (512) - busy beaver function .
It is clear that BB (1024) >> BB (512). But how fast does the BB function itself grow? It turns out that it grows faster than everything we met. The function BB itself is algorithmically unsolvable, it cannot be calculated on a computer. But with an increase in the length of the permissible program, we can implement more and more new ideas. So BB grows faster than any algorithmically solvable function.
Okay, stop doing tiny numbers, let's do big ones. Ah, did I say that already? It would be great to run BB (BB (n)). But since BB is not computable, there are technical difficulties with this (such a function is computable in Turing machines with oracles - do not confuse OrACs with Oracle DBMS).
But you can do it easier, instead of a program, consider a formula with quantifiers of length n. The formula with quantifiers is not important whether something is computable or not. So you can at least take the function BB (10000000000), and apply it to yourself BB (BB (BB (1000000))) times. And this is just what first came to mind.
The largest number, which can be designated by a formula of not more than n characters, is denoted by FOOT (n).
For the next article I would like to understand what to focus on, please take part in the survey.

From completely harmless things can grow monsters. Take, for example, the game in substrings. Write a string of letters a and b and select the substrings from character 1 to character 2, from 2 to 4, from three to 6, from n to 2n, while the length of the main string is enough. Our task is to ensure that in these shifts the shorter one does not enter into any longer one. I even wrote a SQL analyzer:
declare @s varchar(max) = 'abbbaaaaaaab' declare @n int=1 declare @sub table (n int, sub varchar(max)) while @n*2<=len(@s) begin insert into @sub select @n,substring(@s,@n,@n+1) set @n=@n+1 end select *,(select max(sub) from @sub I where In>On and charindex(O.sub,I.sub)>0) as FoundMatch from @sub O order by 1 Here is an example of the output:
')

As you can see, substrings 1 and 5 did not pass the test. We can remove the last character, and the resulting string of 11 characters 'abbbaaaaaaa' will pass the check. It turns out that this is the longest possible string in the two-character alphabet that satisfies this condition.
For a single-character alphabet, the maximum string length is 3, and then for purely technical reasons. It turns out that the maximum length is finite for an alphabet of any number of letters. So, we have:
f(1)=3
f(2)=11
f(3)=???
Check your intuition, how long a string can be made in an alphabet of three letters. 100? 1000? In fact, a lot more than Googol, and a lot more than GoogolPleh.
f(3)>2 uparrow7198$15883
And I have to take the time to show the power of the shooters.
Arrows (hyperoperations)
We use multiplication to not write a lot of addition operations:
2∗5=2+2+2+2+2
We use exponentiation to not write a lot of multiplications:
23=2∗2∗2
Considering addition as an operation of level 0, multiplication - 1, raising to a power - 2, we can introduce an operation “arrow”, for example,
3 uparrow3=3(33)=327=7′625′597′484′987
Note that parentheses are already important. The next level is the operation of two arrows:
3 uparrow uparrow3=3 uparrow(3 uparrow3)=3 uparrow7625597484987=33...3
The last pyramid of triples has a height of 7 billion, and this number is already much, much more, and googol and googolplex. Let's designate this huge number as Darkness (it was such a numeral in the old Russian language) and try to take one more step:
3 uparrow33=3 uparrow uparrow uparrow3=3 uparrow uparrow(3 uparrow uparrow3)=3 uparrow uparrowdarkness=3 uparrow3 uparrow3... uparrow3
(and so the darkness of times) ... There is even to imagine how great this number. Please note that when the shooter is many, we write a repeater at the top. So you can understand how big
f(3)>2 uparrow7198$15883
And even more
With the help of arrows, only the smallest of the big numbers are created, if I may say so. The growth rate of functions is measured by some scale - by comparison with fast-growing functions . The first function in this hierarchy corresponds to addition, the second to multiplication, the third to the arrow, the n-ny to the n-2 arrows (approximately, not exactly). But you can define
fw(n)=fn(n)
Such a function for for n = 3 is comparable with one arrow, for n = 4 with two arrows, and with the growth of the parameter n, it is ahead of the growth of the function with any static number of arrows.
You can go even further: fw,fw+1,fw+n,fw2,fw2,fww,fwww,f epsilon These functions are indexed by ordinals, or in Russian literature by ordinal numbers. The picture with the structure of the initial ordinal numbers is preceded by an article, but they extend much further, and further begins
Little mystic
The endless pyramid of 'omeg' gives some kind of ordinal e p s i l o n 0 . Read about the function , the growth of which is measured by this ordinal. It turns out that a function grows so fast that formal arithmetic cannot, in principle, prove that such a function is defined at all!
Of course, you know about the Gödel theorem that there are unprovable assertions. But, as a rule, the only example of such a statement is the very construction of Gödel (“I am unprovable”). The Goodstein theorem is a good example of this.
Moreover, it turns out that the ordinals somehow measure the power of theories . The 'strength' of formal arithmetic is equal to e p s i l o n 0 , the simplified Kripke-Platek set theory has the power of the Feferman-Schutte ordinal, and so on.
Tin - Maths Harness - Competition in C
A competition was held to generate large numbers. No, programming for the Turing machine is still too cruel, so the C language was used for an abstract infinite machine with sizeof (int) = infinity. You could also use malloc (), and the amount of memory, like the stack, is unlimited. Only the length of the program was limited - the program had to fit in 512 bytes (excluding spaces), but the use of a preprocessor was allowed (#define).
The results are published on the website of mathematics . At the same time check out the design of the site of this mathematics. The results are here . Here is the text of the program that has taken the second place, giving the number about
f w w ( 10 500 )
typedef int J; JP(J x,J y) { return x+y ? x%2 + y%2*2 + P(x/2,y/2)*4 : 0 ;} JH(J z) { return z ? z%2 + 2*H(z/4) : 0 ;} JI(J f,J e,J r){ return f ? P(P(f,e),r) : r ;} JM(J x,J e) { return x ? I(x%2, M(e,0), M(x/2, e+1)) : 0 ;} JD(J,J); JE(J f,J e,J r,J b) { return e ? E(1, D(e,b), I(b-1, D(e,b), I(f-1,e,r)), b) : I(f-1,e,r) ; } JD(J x,J b) { return x ? E( H(H(x)), H(H(x)/2), H(x/2), b) : 0 ;} JF(J x,J b) { return x ? F(D(x,b+1),b+1) : b ;} JG(J x) { return F(M(x,9), 9) ;} J f(J n,J x) { return n ? f(n-1, G(x ? f(n,x-1) : n)) : G(x) ;} J g(J x) { return f(x,x) ;} J h(J n,J x) { return n ? h(n-1, g(x ? h(n,x-1) : n)) : g(x) ;} J main(void) { return h(g(9),9) ;} The text of the winner’s program is longer, I just wanted to show how it begins:
#define R { return #define PP ( #define LL ( #define TS (v, y, c, #define C ), #define X x) #define F );} But even the organizer of the competition (written very big ) found it difficult to estimate how large the number turned out.
Busy beavers
Okay, stop doing tiny numbers, let's do big ones. Imagine that a universal contest is organized to write a program for generating the largest number. Since the number of programs is not longer than 512 characters, of course, there is an absolute winner. Let's designate it as BB (512) - busy beaver function .
It is clear that BB (1024) >> BB (512). But how fast does the BB function itself grow? It turns out that it grows faster than everything we met. The function BB itself is algorithmically unsolvable, it cannot be calculated on a computer. But with an increase in the length of the permissible program, we can implement more and more new ideas. So BB grows faster than any algorithmically solvable function.
BIG FOOT
Okay, stop doing tiny numbers, let's do big ones. Ah, did I say that already? It would be great to run BB (BB (n)). But since BB is not computable, there are technical difficulties with this (such a function is computable in Turing machines with oracles - do not confuse OrACs with Oracle DBMS).
But you can do it easier, instead of a program, consider a formula with quantifiers of length n. The formula with quantifiers is not important whether something is computable or not. So you can at least take the function BB (10000000000), and apply it to yourself BB (BB (BB (1000000))) times. And this is just what first came to mind.
The largest number, which can be designated by a formula of not more than n characters, is denoted by FOOT (n).
B I G F O O T = F O O T 10 ( 10 100 )
PS
For the next article I would like to understand what to focus on, please take part in the survey.
Source: https://habr.com/ru/post/445398/
All Articles