Labyrinths: classification, generation, search for solutions

This classic post describes in detail the most popular ways of creating and passing mazes. The article is divided into four parts: classification, generation algorithms, labyrinth solving algorithms, and other operations with mazes.

Labyrinth classification

Labyrinths in general (and therefore the algorithms for their creation) can be divided into seven different classifications: dimensions, hyperdimensionality, topology, tessellation, routing, texture and priority. The labyrinth can use one element from each class in any combination.
Dimension: the dimension class essentially determines how many dimensions in space the maze fills. There are the following types:

• 
  ')
  Two-dimensional : most labyrinths, both paper and real, have this dimension, that is, we can always display a plan of the maze on a piece of paper and move along it without crossing any other maze corridors.
• Three-dimensional : the three-dimensional labyrinth has several levels; in it (at least in the orthogonal version), except for four sides of the world, the aisles can go down and go up. The 3D maze is often visualized as an array of 2D levels with up and down stairs.
• 
  
  Higher dimensions : you can create four-dimensional mazes and even more multi-dimensional. Sometimes they are visualized as 3D labyrinths with “portals” leading through the fourth dimension, for example, portals to the “past” and “future”.
• 
  
  Interlacings : labyrinths with interlacings are essentially two-dimensional (or, more precisely, 2.5-dimensional) labyrinths, in which, however, the aisles can overlap each other. When displayed, it is usually quite obvious where the dead ends are and how one passage is above the other. Labyrinths from the real world, in which there are bridges that connect one part of the maze with another, are partly interlacing.

Hyper-Dimensionality: classification by hyperdimension corresponds to the dimension of an object moving through a maze, and not the maze itself. There are the following types:

• 
  
  Non-hyperlabirinths : Almost all labyrinths, even those created in high dimensions or having special rules, are usually non-hyperlabirinths. In them we work with a point or a small object, for example, a ball or the player himself, who move from point to point, and the paved route forms a line. At each point there is an easily calculated number of choices.
• Hyper-mazes: Hyper-mazes are labyrinths in which the object to be solved is not just a point. The standard hyperlabirinth (or a first-order hyperlabirinth) consists of a line that, when moved along a path, forms a surface. The hyperlabyrinth can only exist in 3D or in a medium with a higher dimension, and the entrance to the hyperlabyrinth is often not a point, but a line. The hyperlabyr is fundamentally different because it takes into account and simultaneously works with several parts along the line, and at any given time there is a practically infinite number of states and variants of what can be done with the line. The solution line is infinite, or its end points are outside of the hyper-maze to avoid line-to-point compression, because in this case it can be considered a non-hyper-maze.
• Hyper-hyperlabing: hyperlabing can be of arbitrarily high dimension. The hyper-hyperlabing (or second-order hyper-labyrinth) again increases the dimension of the object being solved. Here the solvable object is a plane that, when moving along the path, forms a three-dimensional figure. The hyper-hyperlabirint can exist only in 4D or higher dimensional environments.

Topology: A topology class describes the geometry of a maze space in which it exists as a whole. There are the following types:

• 
  
  Common : This is a standard maze in Euclidean space.
• 
  
  Planair : the term "planair" describes any maze with an unusual topology. This usually means that the edges of the maze are connected in an interesting way. Examples: labyrinths on the surface of a cube, labyrinths on the surface of the Mobius strip and labyrinths equivalent to those on the torus, where the left and right, upper and lower sides are connected in pairs.

Tessellation: the classification of the geometry of the individual cells that make up the maze. Existing types:

• 
  
  Orthogonal : This is a standard rectangular grid in which cells have aisles that intersect at right angles. In the context of tessellation, they can also be called gamma-mazes.
• 
  
  Delta : Delta mazes are made up of connected triangles, and each cell can have up to three passes connected to it.
• 
  
  Sigma : sigma mazes are composed of connected hexagons; each cell can have up to six passes.
• 
  
  Theta : theta labyrinths consist of concentric circles of aisles in which the beginning or end is in the center, and the other is on the outer edge. Cells usually have four possible aisle junctions, but there may be more due to the larger number of cells in the outer rings of the aisles.
• 
  
  Ypsilon : The upsilon labyrinths consist of connected octagons or squares, each cell can have up to eight or four passes.
• 
  
  Zeta : The Zeta Maze is located on a rectangular grid, only in addition to the horizontal and vertical aisles are allowed diagonal passes at a 45 degree angle.
• 
  
  Omega : The term "omega" refers to almost any maze with constant non-orthogonal tessellation. Delta, sigma, theta, and upsilon labyrinths are of this type, as are many other schemes that can be devised, for example, a maze consisting of pairs of right triangles.
• 
  
  Crack : crack labyrinth is an amorphous labyrinth without constant tessellation, in which walls and aisles are located at random angles.
• 
  
  Fractal : A fractal labyrinth is a labyrinth made up of smaller labyrinths. A fractal labyrinth of nested cells is a labyrinth, in each cell of which other labyrinths are located, and this process can be repeated several times. An infinitely recursive fractal labyrinth is a true fractal in which the contents of a labyrinth copy itself, creating essentially an infinitely large labyrinth.

Routing: Routing classification is probably the most interesting aspect of maze generation. From is associated with the types of passes within the geometry defined in the categories described above.

• 
  
  Ideal : A maze without loops or closed chains and without unreachable areas is called “ideal.” Also called a maze with a single connection (simply-connected Maze). From each point there is exactly one path to any other point. The maze has only one solution. From the point of view of programming, such a maze can be described as a tree, connecting many cells or vertices.
• 
  
  Braid : Braided means that there are no dead ends in the maze. Also called a maze with multiple connections (purely multiply connected Maze). In such a maze, passages are used that close up and return to each other (hence the name “woven”), they force you to spend more time walking in circles instead of falling into dead ends. A quality woven labyrinth can be much more complex than a perfect maze of the same size.
• 
  
  Single route (Unicursal) : single route means a labyrinth without forks. The single-path labyrinth contains one long, wriggling passage that changes direction throughout the labyrinth. It is not very complicated only if you do not accidentally turn back halfway and return to the beginning.
• 
  
  Sparse: a rarefied labyrinth does not make passes through each cell, that is, some of them are not created. This implies the presence of unattainable areas, that is, it is in some sense opposite to the woven maze. A similar concept can be applied when adding walls, so you can get an uneven maze with wide aisles and rooms.
• Partially woven: Partially woven labyrinth is a mixed labyrinth, in which there are loops and dead ends. The word “woven” can be used to quantify, that is, a “labyrinth with strong weaving” is a labyrinth with many loops or recessed walls, and there are only a few in the “labyrinth with weak weaving”.

Texture: Texture classification describes the style of aisles with different routing and geometry. Texture is not just parameters that can be turned on or off. Here are some examples of variables:

• 
  
  Bias : In a labyrinth with displaced passages, straight aisles tend to go more in one direction than in others. For example, in a labyrinth with high horizontal displacement, we will have long passes from left to right, and only short passes from top to bottom connecting them. Such a maze is usually more difficult to pass "across the fibers."
• 
  
  Spans : The “spans” indicator determines how long long passes will take before the turns are forced. In a labyrinth with a low span, there will be no straight passages longer than three or four cells, and it will look very random. In the labyrinth with a high rate of passage over the course of the labyrinth there will be a large percentage of long passes, which will make it look like a microchip.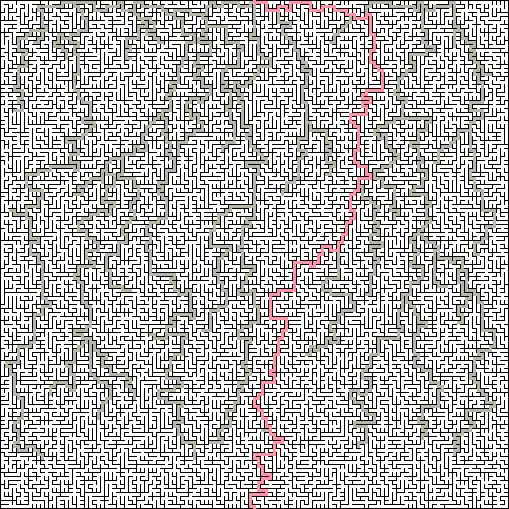
• 
  
  Elite: The maze "elite" indicator determines the length of the decision regarding the size of the maze. Elite labyrinths usually have a short, direct solution, and in non-elite labyrinths the solution goes through a large part of the area of ​​the maze. A quality elite maze can be much more difficult than non-elite.
• 
  
  Symmetry : a symmetrical labyrinth has symmetric passages, for example, in the symmetry of rotation about the center, or reflected along the horizontal or vertical axes. A labyrinth can be partially or completely symmetrical, and can repeat a pattern any number of times.
• 
  
  Homogeneity: a homogeneous algorithm generates all possible mazes with equal probability. A maze can be called having a uniform texture if it looks like a typical maze generated by a homogeneous algorithm. Theoretically, a non-uniform algorithm can also generate all possible labyrinths in any space, but not with equal probability. Heterogeneity can go even further - it is possible the existence of labyrinths that the algorithm will never generate.
• Fluidity (River): “fluidity” means that when creating a labyrinth, the algorithm will search and clean up neighboring cells (or walls) to the current one, that is, it will flow (hence the term “fluidity”) into still uncreated parts of the maze, like water. In an ideal maze with a lower turnover index, there will usually be a lot of short dead ends, and in a more fluid maze there will be fewer dead ends, but they will be longer.

Priority: this classification shows that labyrinth creation processes can be divided into two main types: adding walls and cutting passages. Usually, when generating it, it comes down only to the difference in algorithms, and not to noticeable differences in the labyrinths, but still it is useful to take this into account. The same maze is often generated in both ways:

• Adding Walls: Algorithms for which walls are a priority start from a blank area (or external border), adding walls to the process. In the real world, real labyrinths made up of hedges, floors, or wooden walls are definitely adding walls.
• Cutting aisles: the algorithms, whose priority is the aisles, start with a solid block and, in the process, cut aisles in it. In the real world, such labyrinths are mine tunnels or labyrinths inside pipes.
• 
  
  Pattern: Of course, labyrinths can simultaneously cut out passages and add walls; some computer algorithms do that. A pattern of a maze is a graphic image that is not a maze, which in the fewest steps turns into a real maze, but still retains the texture of the original graphic template. Complex maze styles, such as intersecting spirals, are easier to implement in your computer as templates, rather than trying to create the correct maze, while at the same time preserving its style.

Other: The above is by no means an exhaustive list of all possible classes or elements within each class. These are only the types of labyrinths that I created myself. Notice that almost every type of labyrinth, including labyrinths with special rules, can be expressed as a directed graph with a finite number of states and a finite number of choices in each state, and this is called labyrinth equivalence . Here are a few other classifications and types of labyrinths:

• 
  
  Directionality : you can only move in certain directions in one direction. From the point of view of programming, such a labyrinth will be described by a directed graph, in contrast to an undirected graph describing all other types.
• 
  
  Segmentation : a maze may have different parts corresponding to different classes.
• 
  
  Labyrinths of infinite length: we can create an infinitely long labyrinth (a finite number of columns and any number of rows), but at the same time keep in memory only one part of the maze, “scrolling” from one end to another and destroying the previous lines when creating the next. One example is a modified version of the Hunt and Kill algorithm. You can imagine a potentially endless labyrinth in the form of a long film, made up of individual frames. Only two consecutive frames are stored in memory at a time. Let's run the Hunt and Kill algorithm, although it creates bias inclined to the top frame, so it ends first. After completion, the frame is no longer needed; you can print it out or do something else with it. Anyway, we discard it, make a partially created lower frame with a new upper frame and clear the new lower frame. We repeat the process until we decide to stop, after which we wait until Hunt And Kill completes both frames. The only limitation is that the labyrinth will never have a path branching out into the entrance for a length of more than two frames. The simplest way to create an infinite maze is the Eller algorithm or the Sidewinder algorithm, because they already create mazes one line at a time, so you can simply allow them to add lines to the maze indefinitely.
• 
  
  Virtual fractal labyrinths: virtual is a maze in which the entire maze is not stored in memory at the same time. For example, it can store only a portion of the 100x100 aisles near your location in a simulation where you walk through a large maze. Expansion of nested fractal labyrinths can be used to create virtual labyrinths of enormous size, for example, billion per billion passes. If we built a real copy of the maze of a billion to a billion passes (with a distance of six feet between the passes), then it would fill the surface of the Earth more than 6000 times! Consider a maze of 10 ⁹ by 10 ⁹ passes, or a nested maze with just 9 levels. If we want to have at least a part of 100x100 in size around us, then it is enough to create at the lowest level a sub-maze of 100x100 passes and seven 10x10 mazes in which it is embedded in order to know exactly where the walls are within the part of 100x100. (In fact, it’s better to have four neighboring parts of 100x100 in size, forming a square in case you are near the edge or corner of the part, but the same concept applies.) To ensure the maze remains constant and unchanged when moving along it, we have the formula defining a random generating number (seed) for each coordinate at each nesting level. Virtual fractal labyrinths are similar to the Mandelbrot fractal, in the images of which it exists virtually, and we need to visit a certain coordinate at a high enough magnification. so he manifested.

Algorithms for creating labyrinths

Here is a list of generalized algorithms for creating various classes of labyrinths described above:

• 
  
  Ideal : to create a standard perfect maze it is usually necessary to “grow” it, ensuring there are no loops and no isolated areas. We start with the outer wall and randomly add a fragment of the wall relating to it. We continue to randomly add wall segments to the labyrinth, but check that each new segment touches one end of the existing wall and its other end is in the still uncreated part of the maze. If you add a wall segment, both ends of which are separated from the rest of the maze, this will create an unconnected wall with a loop around, and if you add a segment, both ends of which touch the maze, then this will create an unattainable area. This is the method of adding walls; almost the same way as cutting passages, in which parts of the passages are cut in such a way that only one end touches the existing passage.
• 
  
  Wicker : to create a labyrinth without dead ends, in fact, you need to add wall segments to the labyrinth randomly, but make sure that each new added segment does not create a dead end. I create them in four stages: (1) I start from the outer wall, (2) walk around the maze and add separate wall segments that touch each wall top so that there are no open rooms or small pillars in the labyrinth, (3) go around all possible wall segments in random order, adding a wall where it does not create a dead end, (4) or start the procedure for removing isolated areas at the end so that the maze is correct and has a solution, or I do smarter in step (3) and do so that the wall is added only when it cannot lead to molded area.
• 
  
  Single route : One way to create a random single route maze is to create a perfect maze, close the exit so that only one entrance remains, and then add walls dividing each passage into two parts. This turns each impasse into a U-shaped turn, and we have a single-route passage, starting and ending at the beginning of the original maze, which will follow the same path as moving along the wall of the original maze. The new single-route labyrinth will have twice the size relative to the original ideal maze. You can add small tricks so that the beginning and the end are not always next to each other: when creating the perfect maze, we will never add segments that connect to the right or bottom walls, so the resulting maze will have a simple solution that follows the wall. Put the entrance in the upper right corner, and after splitting it in half to create one route, remove the right and the bottom walls. The result is a single-route maze, starting in the upper right corner and ending in the lower left.
• 
  
  Sparse: sparse labyrinths are created by the decision not to grow a maze in areas that will violate the rule of sparseness. For a holistic implementation of this, when selecting a new cell to be cut, first check all the cells located in the semicircle of the selected cell radius located in front of the current direction. If one of these cells is already part of the maze, then we do not allow to look at these cells, because otherwise they will be too close to the existing cell, which means they will turn the maze into un-thinned.
• 3D : three-dimensional labyrinths and labyrinths of higher dimension can be created in the same way as a standard two-dimensional perfect maze, only from each cell one can randomly move to six, and not four orthogonal cells. Because of the extra dimensions in these mazes, aisle cutting is usually used.
• 
  
  Intertwined : intertwined labyrinths are essentially created as ideal labyrinths with cutting passages, only when cutting passages we are not always limited to the existing passage, because we have the opportunity to go under it and still maintain the ideality of the maze. In a monochrome raster image, an interlaced maze can be represented in four lines per pass (two lines per pass is enough for a standard perfect maze): one line for the passage itself, and the other three lines clearly show when another neighboring passage goes under it and does not simply form a dead end next to the first pass. For the sake of aesthetics, before cutting under the ready-made passage, you can look ahead to be sure. that you can continue cutting while under it; so you can avoid dead ends, located directly under the other passages. Also, after cutting under the passage, you can invert the pixels adjacent to the intersection so that new passages pass over the old ones, and not under them.
• 
  
  Crack : Crack- , , . , , , «» . , , . , - . , , ; . , .
• 
  
  : «» , , . , - : (1) , . (2) , , , , , (.. ). (3) , , . , .
• 
  
  : — 3D-, -, , . 3D- , , . , , . , . , ( ), , , .
• 
  
  Planair : Planair- , . — . , .
• 
  
  : , , , -, , , , . , . , , , , , .

There are many ways to create perfect mazes, and each one has its own characteristics. Below is a list of specific algorithms. All of them described the creation of a maze by cutting out passages, however, unless otherwise indicated, each can also be done by adding walls:

• 
  
  Recursive backtracker : - recursive backtracker, , . , , . , , . , . , . , , , . , . Recursive backtracking , , , .
• 
  
  : , . , «» , , . , , ( ). , . , , . , - , , . , , . , . , - (union-find algorithm): , . . , - .
• 
  
  () : , . . ( , ). , , , . , . ( ), . , , log(n). , , . seed .
• 
  
  () : . , . , . . , , , . , . , , . . , , , , , .
• 
  
  () : , , . , . . : (1) "": , (2) "": , , «», (3) "": , «» . , «», «». «» «» . «» «» «» «». , «» ( «» , , «»). , . , : , , , . , , , .
• 
  
  - : , , . , . . , . , . , , . ( , , , .) , , , . - , , . , , , . , , .., , , , . , .
• 
  
  : -, ( , ), . . . , , , . ,, , . , , . , . , . , -, , . -, . , , , .
• 
  
  Hunt and kill : , , . , , . recursive backtracker, . «» , . . , «» . , , recursive backtracker. , «». - , , , . , , , recursive backtracker.
• 
  
  
  (Growing tree algorithm) : , . . . . , . , . , . , , recursive backtracker. , , . , , , , . , , , . , , .
• 
  
  (Growing forest algorithm) : , , . , , . , «»; , , . , «» «». «» «» , «» . , , , , . «» , «». , «». , . , «» «», . , , .
• 
  
  Heller's algorithm : this is a special algorithm, because it is not only the fastest of all others, but also has no obvious bias or flaws; in addition, when creating it, memory is used most efficiently. It doesn’t even require that the entire maze be in memory, it uses a volume proportional to the size of the line. It creates a maze line by line, after the generation of the string is completed, the algorithm no longer takes it into account. Each cell in the row is contained in the set; two cells belong to the same set if there is a path between them through the already created maze. This information allows you to cut passes in the current line without creating loops or isolated areas. In fact, this is quite similar to the Kruskal algorithm, only here it is formed one line at a time, while Kraskal looks through the entire maze. Creating a string consists of two parts: we randomly connect adjacent cells within a row, i.e. cut horizontal passes, then randomly connect the cells between the current and next lines, i.e. cut vertical passages. When cutting horizontal passes, we do not connect cells that are already in the same set (because otherwise a loop will be created), and when cutting vertical passes we must connect a cell if it has a unit size (because if we leave it, it will create an isolated area). When cutting horizontal passages, we connect cells, if they are in the same set (because there is now a path between them), and when cutting vertical passages when we are not connected to a cell, we place it into a separate set (because now it is separated from the rest of the maze ). The creation begins with the fact that before connecting the cells in the first row, each cell has its own set. Creation is completed after the cells are connected in the last row. There is a special completion rule: by the time of completion, each cell must be in the same set to avoid isolated areas. (The last line is created by combining each of the pairs of neighboring cells that are not yet in the same set.) It’s best to implement the set using a cyclic doubly linked list of cells (which can be just an array that binds the cells to pairs of cells on both sides of the same set), allowing perform inserting, deleting and checking the presence of neighboring cells in one set in constant time. The problem with this algorithm is the imbalance in the processing of different edges of the maze; To avoid stains in textures, you need to make the connection and skip the connection of the cells in the correct proportions.
• 
  
  Recursive division: this algorithm is somewhat similar to recursive backtracking, because in both of them stacks are used, only it works not with aisles, but with walls. We start by creating a random horizontal or vertical wall intersecting the accessible area in a random row or column, and place random spaces along it. Then we recursively repeat the process for the two subdomains generated by the dividing wall. For best results, you should add a deviation in the choice of horizontal or vertical based on the proportions of the area, for example, an area whose width is twice the height should be more often divided by vertical walls. This is the fastest algorithm without deviations in directions, and often it can even compete with labyrinths based on binary trees, because it creates several cells at the same time, although it has an obvious drawback in the form of long walls that intersect the interior of the labyrinth. This algorithm is a kind of nested fractal labyrinths, but instead of constantly creating labyrinths of fixed-size cells with labyrinths of the same size inside each cell, it randomly divides a given area into a random-sized labyrinth: 1x2 or 2x1. Recursive division cannot be used to cut aisles, because it leads to the creation of an obvious solution that either follows along the outer edge, or otherwise intersects the inside.
• 
  
  Labyrinths based on binary trees : in fact, these are the simplest and fastest of the possible algorithms, but the mazes that are created have a texture with very high bias. For each cell, we cut a passage either up or left, but never in both directions. In the wall version, a wall segment is added for each vertex, leading down or to the right, but not in both directions. Each cell is independent of all other cells, because we do not need to check the state of any other cells when creating it. Therefore, this is a true algorithm for generating labyrinths with no memory, not limited by the size of the labyrinths being created. In fact, this is a binary tree, if we consider the upper left corner as a root, and each node or cell has one unique parent node, which is a cell above or to the left of it. Labyrinths based on binary trees are different from the standard ideal mazes, because more than half of the cell types cannot exist in them. For example, there will never be intersections in them, and all dead ends have passages leading up or to the left and never leading down or to the right. Labyrinths tend to have passages leading diagonally from the upper left to the lower right corner, and along them it is much easier to move from the lower right to the upper left corner. You can always move up or left, but never simultaneously in both directions, so you can always deterministically move diagonally up and left without colliding with barriers. You will have the opportunity to choose and get into dead ends by moving down and to the right. Keep in mind that if you turn the binary tree maze upside down and count the aisles as walls, and vice versa, the result will essentially be another binary tree.
• 
  
  Sidewinder Labyrinths: This simple algorithm is very similar to the binary tree algorithm, but a bit more complicated. The labyrinth is generated one line at a time: for each cell, it is randomly selected whether to cut a passage leading to the right. If the passage is not cut, then we consider that we have just completed a horizontal passage formed by the current cell and all the cells on the left that cut the passages leading into it. Randomly select one cell along this passage and cut a passage leading up from it (this should be the current cell if the neighboring cell has not cut the passage). While the labyrinth of a binary tree always rises up from the leftmost cell of a horizontal passage, the sidewinder maze rises up from a random cell. In the binary tree, the labyrinth in the upper and left edges has one long passage, and in the sidewinder labyrinth there is only one long passage along the upper edge. Like the binary tree labyrinth, the sidewinder maze can be error-free and deterministically solved from the bottom up, because there will always be exactly one pass leading up in each row. The sidewinder maze solution never loops or visits the same line more than once, but it "squirms from side to side." The only cell type that cannot exist in the sidewinder maze is a dead end with a downward walkway, because it will be against the rule that every pass that leads upwards returns us to the beginning. Sidewinder mazes are prone to the appearance of an elite solution, in which the right path turns out to be very straightforward, but next to it there are many long error paths leading from top to bottom.

Algorithm	% dead ends	Type of	A priority	Is there biasedness?	Homogeneous?	Memory	Time	% solutions
Single route	0	Tree	Walls	Yes	Never	N ^ 2	379	100.0
Recursive Backtracker	ten	Tree	The walkways	Yes	Never	N ^ 2	27	19.0
Hunt and kill	11 (21)	Tree	The walkways	Yes	Never	0	100 (143)	9.5 (3.9)
Recursive division	23	Tree	Walls	Yes	Never	N *	ten	7.2
Binary tree	25	Lots of	Both	Not	Never	0 *	ten	2.0
Sidewinder	27	Lots of	Both	Not	Never	0 *	12	2.6
Eller's algorithm	28	Lots of	Both	Not	Not	N *	20	4.2 (3.2)
Wilson's algorithm	29	Tree	Both	Yes	Yes	N ^ 2	48 (25)	4.5
Aldous-Brodera Algorithm	29	Tree	Both	Yes	Yes	0	279 (208)	4.5
Kruskal Algorithm	thirty	Lots of	Both	Yes	Not	N ^ 2	33	4.1
Prima algorithm (true)	thirty	Tree	Both	Yes	Not	N ^ 2	160	4.1
Prima algorithm (simplified)	32	Tree	Both	Yes	Not	N ^ 2	59	2.3
Prima algorithm (modified)	36 (31)	Tree	Both	Yes	Not	N ^ 2	thirty	2.3
Growing a tree	49 (39)	Tree	Both	Yes	Not	N ^ 2	48	11.0
Growing forest	49 (39)	Both	Both	Yes	Not	N ^ 2	76	11.0

This table briefly presents the characteristics of the algorithms for creating ideal mazes described above. For comparison, a single-route maze algorithm has been added (theoretically, single-route mazes are ideal). Explanation of columns:

• Dead End: This is an approximate percentage of cells that are dead ends in a maze created using this algorithm in the case of an orthogonal 2D maze. The algorithms in the table are sorted by this field. Usually, when adding walls, the percentage is the same as when cutting passages, but if they are significantly different, then the percentage when adding walls is shown in brackets. The value for the tree growing algorithm actually varies from 10% (if the newest cell is always chosen) to 49% (we always choose the oldest cell). With a sufficiently high pass rate, the number of dead ends of the Recursive Backtracker can fall below 1%. The highest probable percentage of dead ends in a two-dimensional orthogonal ideal maze is 66%: this will be a single-route passage with a bunch of dead ends of unit length on both sides of it.
• Type: there are two types of algorithms for creating perfect mazes: a tree-based algorithm grows a maze like a tree, always adding to what it already has and having the correct perfect maze at each stage. The set-based algorithm performs constructions where it wants, tracking parts of the maze, connected to each other, to connect everything and create the right maze at the time of completion. Some algorithms, such as the forest growing algorithm, use both approaches simultaneously.
• Priority: most algorithms can be implemented either as cutting passes, or as adding walls. Very few can be implemented only as one or the other approach. In single-route labyrinths, the addition of walls is always used, because they involve splitting the aisles by walls into two parts, but the basic labyrinth can be created in any way. Recursive Backtracker cannot be implemented with the addition of walls, because in this case it tends to create a solution path that follows the outer edge, and the entire inner part of the labyrinth is connected to the border with a single pass. Similarly, recursive division can be realized only through the addition of walls, because this algorithm performs the division in half. Strictly speaking, for the same reason, Hunt and Kill can be realized only through cutting passages, however, it can also use the addition of walls, if special efforts are made to give equal growth inwards from all walls of the borders.
• Lack of bias: does the algorithm equally perceive all directions and sides of the maze so that subsequent analysis of the maze cannot detect any bias of the passages. The binary tree algorithm is extremely biased, it is easy to move in one corner and difficult to the opposite. Sidewinder is also offset, it is easy to move to one edge and difficult to the opposite. Eller's algorithm is prone to creating passages, roughly synchronizing the starting or ending edges. There is no bias in Hunt and Kill if the hunt is conducted column by column, and also line by line to avoid slight bias along one axis.
• Uniformity: Does the algorithm generate all possible labyrinths with equal probability? “Yes” means that the algorithm is completely homogeneous. “No” means that the algorithm can potentially generate all possible labyrinths within any space, but not with equal probability. “Never” means that there are possible labyrinths that the algorithm can never generate. Note that only algorithms with complete lack of bias can be completely homogeneous.
• Memory: the amount of additional memory or stack needed to implement the algorithm. Efficient algorithms require only the maze's bitmap, while others require a memory size proportional to one row (N) or proportional to the number of cells (N ^ 2). Some algorithms do not even need to remember the whole maze, and they can add parts of the maze indefinitely (such algorithms are marked with an asterisk). Heller's algorithm needs the amount of memory to store the string, but it doesn’t need more, because it is enough to store only one line of the maze. The Sidewinder algorithm also needs to store only one line of the maze, while the binary tree only needs to track the current cell. Recursive division requires a stack up to the size of a string, but it does not need to look at the maze's bitmap.
• Time: this parameter gives an idea of ​​how much time it takes to create a maze using this algorithm, the smaller the number, the faster it works. Unlike other units of measurement, here the numbers are relative to each other (the fastest algorithm is assigned a speed of 10), because time depends on the size of the maze and the speed of the computer. The numbers of the table are taken when creating the mazes from the 100x100 aisles in the latest version of Daedalus. Usually the creation by adding walls takes as much time as it takes to cut aisles, but if the values ​​are very different, then the time to add the walls is indicated in brackets.
• Solution: this is the percentage of cells in the labyrinth through which its solution passes for a typical maze created by an algorithm. Here it is assumed that the labyrinth consists of 100x100 passes. and the beginning and end are in opposite corners. This parameter is an indicator of the "tortuosity" of the solution. The maximum tortuosity has one-route labyrinths, because the solution passes through the entire labyrinth. The smallest possible tortuosity has a binary tree, in which the solution simply crosses the maze and never deviates or stops moving towards the end. Typically, the creation by adding walls has the same properties as cutting aisles, but if the values ​​are very different, then the percentage in the case of adding walls is indicated in brackets.

Algorithms for solving labyrinths

There are many ways to solve labyrinths, and each of them has its own characteristics. Here is a list of specific algorithms:

• 
  
  Following the walls (Wall follower) : this is a simple algorithm for solving labyrinths. The priority for him is a passing maze object (“you”), it is always very fast and does not use additional memory. We start to go along the aisles and when reaching the fork, always turn right (or always left). To apply such a maze solution in the real world, you need to put your hand on the right (or left) wall and constantly keep it on the wall in the process of passing the maze. If desired, you can mark already visited cells and cells that have been visited twice. In the end, you can go back to the decision, following only the cells visited once. This method does not necessarily find the shortest solution, and it does not work at all if the target is located in the center of the maze and is surrounded by a closed circuit, because you will walk around the center and eventually come to the beginning. Following along the wall in the 3D maze can be realized in a deterministic way by projecting 3D passes on the 2D plane, i.e. pretending that the upstairs passages actually lead to the north-west, and the downward paths lead to the south-east, and then apply the usual rules for following along the walls.
• 
  
  Pledge Algorithm : This is a modified version of the following along the wall, capable of jumping between the "islands" to solve those labyrinths that follow the walls are not capable of. This is a guaranteed way to reach the outer edge of any 2D maze from any point inside, but it is not able to perform the inverse task, i.e. find a solution inside the maze. It is well suited to be realized with the help of a robot escaping from a maze, because it can get out of any maze without marking and not remembering the way. We start with a choice of direction and, if possible, always move in that direction. Having rested against the wall, we begin to follow along it, until we can again go in the chosen direction. It should be noted that the following along the wall must begin with the far wall, which we rested. If at this point the passage makes a turn, then it can lead to a turn in the middle of the passage and return the same way we came. When following along the wall, we count the number of turns made, for example, turning left is -1, and turning right is 1. We stop following along the walls and start moving in the chosen direction only when the total amount of turns made is equal, i.e. if you turned 360 degrees or more, then we continue to follow along the wall until we unravel. The calculation ensures that sooner or later we will reach the distant part of the "island" in which we are at the moment and jump to the next island in the chosen direction, after which we will continue to jump between the islands until we rest on the border wall, after which the following along the walls . , , . , — , .
• 
  
  : (Chain algorithm) , ( ) . , , . , . , , . , . ( ) , . . , , . «» , . , , , . , . , .
• 
  
  Recursive backtracker: , . , . : ( ), «», , , «», , . , , «»; «» . (backtracking) , , . , . , , .
• 
  
  (Trémaux's algorithm): . recursive backtracker : , . , . , , . , , , . ( , .) , (.. ), , , , (.. , ). , , , , , . , . , , .
• 
  
  (Dead end filler) : . , . , , . , . , , . , , .
• 
  
  Cul-de-sac filler : , , . dead end filler, , . ( — , , ) , . dead end filler. , , , , . , , , dead end filler.
• 
  
  Blind alley filler : , , . , . — , , . , , cul-de-sac filler, . . , , , , . , , , ( ). , , . , cul-de-sac filler - , collision solver , - .
• 
  
  Blind alley sealer : blind alley filler , , . . . , , blind alley filler, . . , , , , . , , . , . , , . , , .
• 
  
  (Shortest path finder): , , . , , . collision solver, , , «» , ( ), «» , , . «», , . , - , . , , , A* , .
• 
  
  (Shortest paths finder) : , . , , , , , , , - , . , , , «» , , , . , , , , . , .
• Collision solver: "amoeba" solver. . , . «» , ( ). « » ( ), , . «», , , , . ( , «», . , , , .) , shortest paths finder, ( ) ( ).
• Random mouse: , , .. , . 180 , . , , . , , .

		?		?	?	?	?
Random Mouse	one	Not	You	/	Not	Yes	Not
Wall Follower	one	Not	You	/	Yes	Yes	Yes
	one	Not	You	/	Yes	Yes	Yes
	one	Yes	+	Not	Yes	Not	Yes
Recursive Backtracker	one	Yes	You	Not	Yes	Not	Yes
Tremo Algorithm	one	Yes	You	Inside / over	Not	Not	Yes
Dead end filler	All +	Not	Labyrinth	Above	Not	Yes	Yes
Cul-de-sac Filler	All +	Not	Labyrinth	Above	Not	Yes	Yes
Blind Alley Sealer	All +	Yes	Labyrinth	Not	Not	Not	Yes
Blind Alley Filler	Everything	Yes	Labyrinth	Above	Not	Yes	Not
Collision solver	All the shortest	Yes	You +	Not	Not	Not	Yes
Search for the shortest paths	All the shortest	Yes	You +	Not	Yes	Not	Yes
Finding the shortest path	1 shortest	Yes	You +	Not	Yes	Not	Yes

This table briefly lists the characteristics of the maze-solving algorithms described above. By these criteria, it is possible to classify and evaluate algorithms for solving labyrinths. Explanation of columns:

• : , . . , () . Dead end filler cul-de-sac filler ( blind alley sealer ) , , , «+».
• : . Random mouse «», , wall follower «», , . dead end filler cul-de-sac filler «», .
• : : «» ( ) . , ( «») («+») . , .
• : , , . , «», , ( ), , , , . .
• : . , , , , . Wall follower, . Recursive backtracker shortest path(s) finder .
• : . .
• Fast: Is the decision process considered fast? The most efficient algorithms just look at each cell of the maze only once, or they can completely skip parts of it. The execution time should be proportional to the size of the maze, or O (n ^ 2), where n is the number of cells along one side. Random mouse is slow because its completion is not guaranteed, and the blind alley filler potentially solves a maze from each fork.

Other maze operations

In addition to creating and solving labyrinths, you can perform other operations with them:

• 
  
  : « », , Fill FloodFill. FloodFill , , . , , FloodFill , . , , FloodFill , , . «» .
• 
  
  (Isolation remover): , , . , . , . ( , ) , . , , . .
• 
  
  : , , . , , . , . ( , ) . , , , . , .
• 
  
  : , . , , , , . , , . , . , blind alley sealer ( , ). , , .

Algorithm implementations

• Daedalus : all the above algorithms for creating and solving mazes are implemented in Daedalus, a free and downloadable Windows program. Daedalus comes with full source code.