Self-timed circuits. Calculation of logical functions directly on the event graph. Part 3. Decomposition
Let me remind you of an important conclusion from the previous parts. For cyclical sequential behavior that does not contain multiple signals (switching more than two times per cycle), the minimum logical function of each signal can be represented as follows (naturally, in the absence of CSC conflicts):
one)
where a * b * ... * c is an implicant consisting of one or more variables. g + h + ... + i is a possible empty implicant set consisting of one variable. x * f is an implicant of 2 variables, the presence of which in its minimal form is not necessary. All variables, except x, can be included in the formula both in direct and inverse form, depending on the arrangement of signs of the corresponding events. All variables are included in the formula as arguments strictly once.
')
Before going further, we will take a closer look at this phenomenon as decomposition. First of all, decomposition, which preserves self-synchronization, is of interest. When decomposing the logical function NOT-AND-OR as a new element can be identified:
a) one or more implicant
b) several signals (variables) of one implicants,
c) one input inverter.
To begin, consider the special case of the function NOT-AND-OR OR. The behavior of such a logical function (x = a + b + c + d) for the model in question:
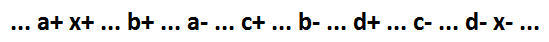
She has several signals as a separate element.
In fact, the selection of a new element in the decomposition is the addition of a new signal (f). In order to preserve the correctness of behavior, semi-modularity, and self-synchronization, the switchings of the newly added signal f must have event-effects. Since decomposition affects only one circuit element (in this case, x) and does not affect the remaining circuit elements, switching the signal f can only cause switching of the signal x. Otherwise, the logical function of a different signal would depend on the signal f. Considering this conclusion, we will try to select any several variables as the new element f, except the variable a. Take for example the variables b and c. They form a logical element f = b + c.
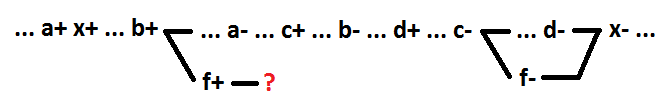
As you can see, for the f + event it is impossible to determine the event-consequence without violating the correctness of the behavior. Any group of signals that does not contain the variable a can not be allocated as a separate element while maintaining self-synchronization.
Such a signal as a in this example will be called inclusive. In general, the inclusive signal for the OR (AND) function is a signal whose switching to 1 (0) changes the value of the function from 0 to 1 (from 1 to 0). To maintain self-synchronization when decomposing the logical function OR (AND) when selecting a new element, it is necessary to use an enabling signal. When selecting a new element, it is also necessary to use only signals that form a linked chain (in the example below, a + b). x = f + c + d, f = a + b.
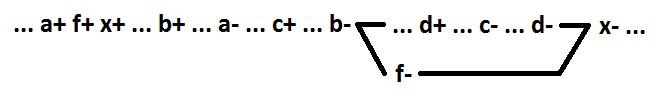
When using signals a + b + d, self-synchronization is not preserved.
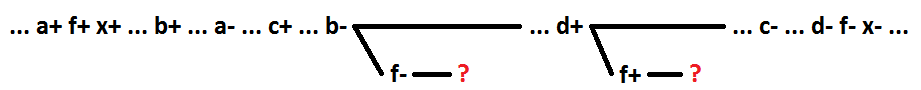
Thus, for consecutive behaviors without multiple signals when decomposing a logical function OR (AND), the selection of the first few elements as the process unfolds, starting with the inclusive one, ensures that the circuit is self-synchronous.
We now consider the function NOT-OR (x =! A +! B). As a separate element (f) with preservation of self-synchronization, only the input inverter that corresponds to the switching signal (x = f +! B, f =! A) can be distinguished. Selection as a separate element of other input inverters will lead to a violation of self-synchronization.
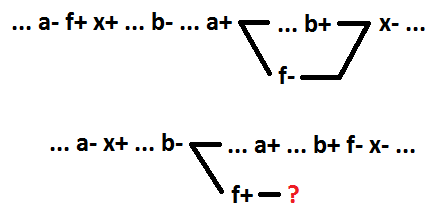
We turn to the consideration of the function AND-OR. Similarly, as an enable signal for the OR function, we define an inclusive signal for the AND-OR function. This implicant, changing the value of which from 0 to 1 leads to a change in the value of the function from 0 to 1. Similarly, as was found for the OR function, for consistent behaviors without multiple signals when decomposing the logical function AND-OR, the selection as a new element of the first few during the deployment process, the implicant, starting with the inclusive one, ensures that the scheme is self-synchronous. Otherwise, self-timing will be broken. In the example below, before decomposition, x = a * b + c. After decomposition x = f + c, f = a * b.
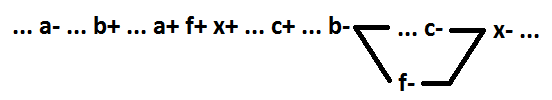
Now for the AND-OR function, we consider the selection as a new element of several variables belonging to the same implicant. Only minimal functions are considered. Below are all possible options for the function x = a * b * c + d (for option 4 - x = a * b * c + d + e, for option 6 - x = a * b * c * d + e) . The selected element f = a * b.

In option 1, switching one of the selected signals (a +) is the cause of the x + event. In option 2, the switching of one of the selected signals (a-) is the cause of the x- event. In variants 3 and 4, the switching of one of the selected signals (a + and a-, respectively) is located between the x + and x- events, and is not the cause of the x- event. Option 5 is a special case of option 4 when the implicant in which the signals are highlighted is inclusive. The remaining option 6 - all switchings of the allocated signals are located between the x- and x + events, and are not the causes of the x + event.
As you can see, in variants 1 and 6, event f- cannot be positioned correctly. Such transformations are not decomposition with preservation of self-synchronization. In variants 2, 3 and 4, self-timing is preserved. But the value of the function x thus turns out to be different from f * c + d (f * c + d + e for 4 variants). For option 2, x = f * (d + c), for option 3, x = c * x + d *! F + x *! F, for option 4, x = (f + d) * (e + c). Such transformations are not decomposition.
Only option 5 is decomposition with self-synchronization (x = f * c + d). In this case, as a separate element in the inclusive implicant, the first several signals are allocated, starting with the enabling one (the signal including the implicant AND, this is the same as the signal including the AND function). But, as shown above, a similar result is achieved in two steps. First, the inclusive implicant is highlighted. In the second step, the first few signals are highlighted in the new element, starting from the inclusive one.
Let us consider the function NOT-AND-OR. Select as a separate element input inverter. Signal a corresponds to the input element x, which is connected to the selected input inverter (f =! A).
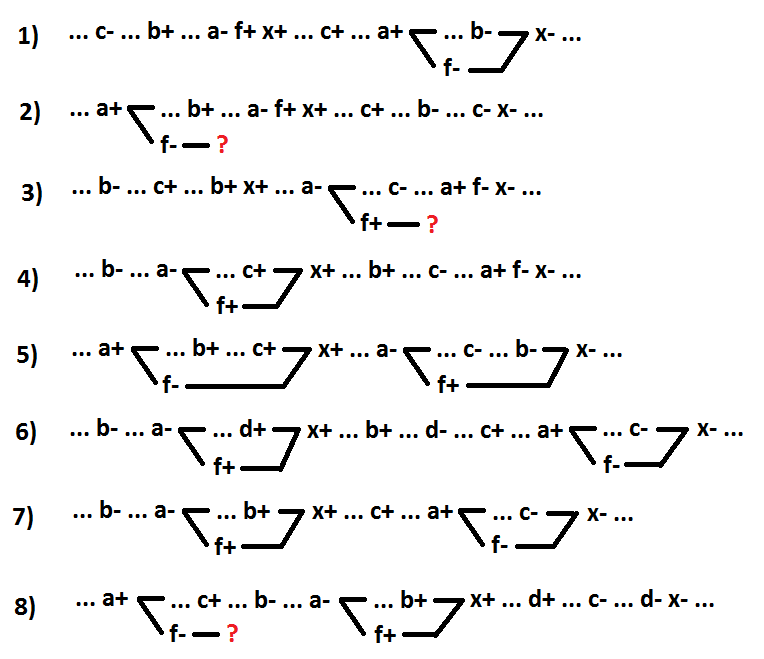
Options 1 and 2 - switching signal a is the cause of the event x + (1 - x =! A + b * c, 2 - x = b *! A + c). Options 3 and 4 - switching the signal a is the cause of the event x- (3 - x =! A + b * c, 4 - x =! A * b + c). Variants 5 and 6 - switching of signal a is located between x + and x- events, and is not the cause of x- event (5 - x = b *! A + c, 6 - x =! A * b + d + c). Option 7 is a special case of option 6, when signal a is an enable signal including implicants (x =! A * b + c). The remaining option 8 - all switchings of the signal a are located between the x- and x + events, and are not the causes of the x + event (x = c *! A * b + d).
As can be seen, options 2, 3 and 8 are not decomposition with preservation of self-synchronization, since it is impossible to correctly position the switching signal f. For option 4, after the transformation x = f * (c + b). For option 5, after the transformation, x = c *! F +! F * x + b * x. For option 6, after the transformation x = (f + c) * (d + b). These transformations (options 4, 5 and 6) are not decomposition. For option 7, after the transformation x = f * b + c. Option 7 is a self-synchronization decomposition. In this case, the inverter is selected as a separate element, corresponding to the switching on signal including the implicants. A similar result is achieved in two steps with the help of the above transformations. First, the inclusive implicant is allocated, then it is allocated the input inverter of the enable signal. For option 1, after the transformation x = f + b * c. Option 1 is also a self-synchronization decomposition. This is a special case of option 7, when including the implicant consists of a single signal.
We systematize the results. For the model under consideration, with the decomposition of the logical function NOT-AND-OR to maintain self-synchronization, only the following transformations are possible - the selection as a separate element:
1 - one or more, starting from the including, overlapping implicant (a special case is for the function NOT-OR selection of several overlapping signals, starting from the including);
2 - in the including several implicant, starting from the including, overlapping signals;
3 - input inverter corresponding to the switching on signal including implicants (a special case is for the NOT-OR function selecting the input inverter corresponding to the turning on signal).
These transformations do not allow the implicant to be included if it was not prior to the conversion. Hence the conclusion: if a logical function contains an implicant that consists of more than one signal and is not inclusive, such a function cannot be fragmented using decomposition that preserves self-synchronization, down to two-input elements. Any logical NOT-AND-OR function for which more than one variable contains only an implicant that can be included can be split up to two-input elements (2I-NO, 2ILE-NO) with the help of decomposition preserving self-synchronization.
Step 1 - if the logical element contains only one implicant (or all implicants consist of one variable) go to step 3, otherwise go to step 2.
Step 2 - we select as a separate element all implicants, except for one, starting from including. Next, work with the newly received element. Go to step 1.
Step 3 - if the element consists of two variables, go to step 5, otherwise proceed to step 4.
Step 4 - select as a separate element all variables, except for one, starting from including. Next, work with the newly received element. Go to step 3.
Step 5 - applies to all received two-input elements.
Step 5.1 - if the input inverters on both inputs, convert the element to dual.
Step 5.2 - if the input inverter is one and corresponds to a signal that is not inclusive, convert the element to dual.
Step 5.3 - input inverter, if any, select as a separate element. Crushing is complete.
Now back to formula 1 at the beginning of the text. If the implicant x * f is missing in a logical expression, then the function looks like this: x = a * b * c + g + h + i. Her behavior:
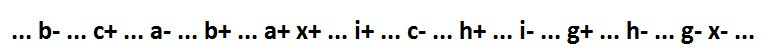
As can be seen, the only implicant consisting of more than one variable (a * b * c) is inclusive. And this function with the help of decomposition can be fragmented to the minimum components while maintaining self-synchronization.
If the implicant x * f is present in a logical expression, then the function looks like this: x = a * b * c + x * f + g + h + i. Her behavior:
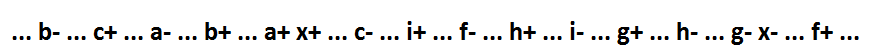
An implicant x * f, which is not inclusive, consists of more than one variable. Such a function cannot be fragmented while maintaining self-synchronization. But apply a self-synchronous transformation: add a signal y - dual to the signal x. Adding a signal y changes the function of only the signal x and the signal whose switching was a consequence of the x- event (the variable x is replaced with the variable y).
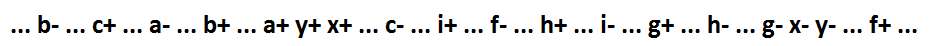
Now x = (f + i + h + g) * y, y = c * b * a + x. The implicants f + i + h + g and c * b * a include and, accordingly, the functions x and y can be fragmented to minimum components while maintaining self-synchronization.
A simplified model of behavior (without parallelism, choice, and multiple signals) allows us to identify properties naturally inherent in binary processes. Synthesis of self-timed circuits in a minimal basis is a natural phenomenon that does not require any design.
one)
where a * b * ... * c is an implicant consisting of one or more variables. g + h + ... + i is a possible empty implicant set consisting of one variable. x * f is an implicant of 2 variables, the presence of which in its minimal form is not necessary. All variables, except x, can be included in the formula both in direct and inverse form, depending on the arrangement of signs of the corresponding events. All variables are included in the formula as arguments strictly once.
')
Before going further, we will take a closer look at this phenomenon as decomposition. First of all, decomposition, which preserves self-synchronization, is of interest. When decomposing the logical function NOT-AND-OR as a new element can be identified:
a) one or more implicant
b) several signals (variables) of one implicants,
c) one input inverter.
To begin, consider the special case of the function NOT-AND-OR OR. The behavior of such a logical function (x = a + b + c + d) for the model in question:
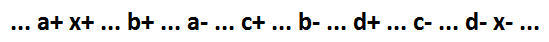
She has several signals as a separate element.
In fact, the selection of a new element in the decomposition is the addition of a new signal (f). In order to preserve the correctness of behavior, semi-modularity, and self-synchronization, the switchings of the newly added signal f must have event-effects. Since decomposition affects only one circuit element (in this case, x) and does not affect the remaining circuit elements, switching the signal f can only cause switching of the signal x. Otherwise, the logical function of a different signal would depend on the signal f. Considering this conclusion, we will try to select any several variables as the new element f, except the variable a. Take for example the variables b and c. They form a logical element f = b + c.
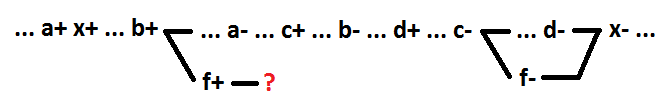
As you can see, for the f + event it is impossible to determine the event-consequence without violating the correctness of the behavior. Any group of signals that does not contain the variable a can not be allocated as a separate element while maintaining self-synchronization.
Such a signal as a in this example will be called inclusive. In general, the inclusive signal for the OR (AND) function is a signal whose switching to 1 (0) changes the value of the function from 0 to 1 (from 1 to 0). To maintain self-synchronization when decomposing the logical function OR (AND) when selecting a new element, it is necessary to use an enabling signal. When selecting a new element, it is also necessary to use only signals that form a linked chain (in the example below, a + b). x = f + c + d, f = a + b.
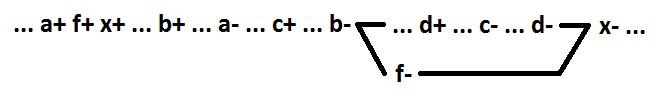
When using signals a + b + d, self-synchronization is not preserved.
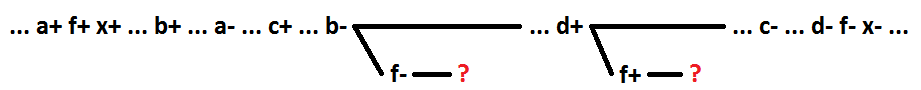
Thus, for consecutive behaviors without multiple signals when decomposing a logical function OR (AND), the selection of the first few elements as the process unfolds, starting with the inclusive one, ensures that the circuit is self-synchronous.
We now consider the function NOT-OR (x =! A +! B). As a separate element (f) with preservation of self-synchronization, only the input inverter that corresponds to the switching signal (x = f +! B, f =! A) can be distinguished. Selection as a separate element of other input inverters will lead to a violation of self-synchronization.
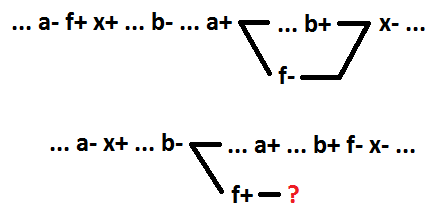
We turn to the consideration of the function AND-OR. Similarly, as an enable signal for the OR function, we define an inclusive signal for the AND-OR function. This implicant, changing the value of which from 0 to 1 leads to a change in the value of the function from 0 to 1. Similarly, as was found for the OR function, for consistent behaviors without multiple signals when decomposing the logical function AND-OR, the selection as a new element of the first few during the deployment process, the implicant, starting with the inclusive one, ensures that the scheme is self-synchronous. Otherwise, self-timing will be broken. In the example below, before decomposition, x = a * b + c. After decomposition x = f + c, f = a * b.
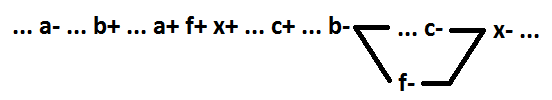
Now for the AND-OR function, we consider the selection as a new element of several variables belonging to the same implicant. Only minimal functions are considered. Below are all possible options for the function x = a * b * c + d (for option 4 - x = a * b * c + d + e, for option 6 - x = a * b * c * d + e) . The selected element f = a * b.

In option 1, switching one of the selected signals (a +) is the cause of the x + event. In option 2, the switching of one of the selected signals (a-) is the cause of the x- event. In variants 3 and 4, the switching of one of the selected signals (a + and a-, respectively) is located between the x + and x- events, and is not the cause of the x- event. Option 5 is a special case of option 4 when the implicant in which the signals are highlighted is inclusive. The remaining option 6 - all switchings of the allocated signals are located between the x- and x + events, and are not the causes of the x + event.
As you can see, in variants 1 and 6, event f- cannot be positioned correctly. Such transformations are not decomposition with preservation of self-synchronization. In variants 2, 3 and 4, self-timing is preserved. But the value of the function x thus turns out to be different from f * c + d (f * c + d + e for 4 variants). For option 2, x = f * (d + c), for option 3, x = c * x + d *! F + x *! F, for option 4, x = (f + d) * (e + c). Such transformations are not decomposition.
Only option 5 is decomposition with self-synchronization (x = f * c + d). In this case, as a separate element in the inclusive implicant, the first several signals are allocated, starting with the enabling one (the signal including the implicant AND, this is the same as the signal including the AND function). But, as shown above, a similar result is achieved in two steps. First, the inclusive implicant is highlighted. In the second step, the first few signals are highlighted in the new element, starting from the inclusive one.
Let us consider the function NOT-AND-OR. Select as a separate element input inverter. Signal a corresponds to the input element x, which is connected to the selected input inverter (f =! A).
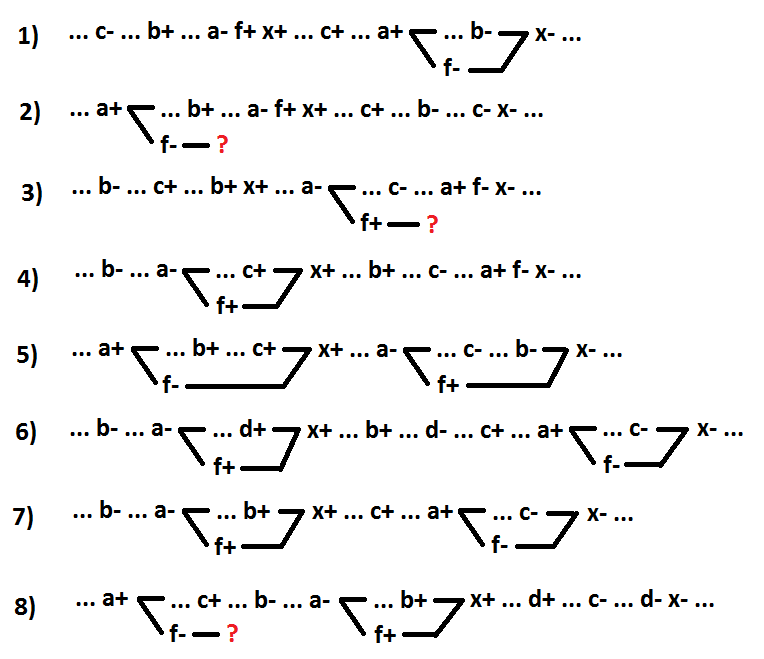
Options 1 and 2 - switching signal a is the cause of the event x + (1 - x =! A + b * c, 2 - x = b *! A + c). Options 3 and 4 - switching the signal a is the cause of the event x- (3 - x =! A + b * c, 4 - x =! A * b + c). Variants 5 and 6 - switching of signal a is located between x + and x- events, and is not the cause of x- event (5 - x = b *! A + c, 6 - x =! A * b + d + c). Option 7 is a special case of option 6, when signal a is an enable signal including implicants (x =! A * b + c). The remaining option 8 - all switchings of the signal a are located between the x- and x + events, and are not the causes of the x + event (x = c *! A * b + d).
As can be seen, options 2, 3 and 8 are not decomposition with preservation of self-synchronization, since it is impossible to correctly position the switching signal f. For option 4, after the transformation x = f * (c + b). For option 5, after the transformation, x = c *! F +! F * x + b * x. For option 6, after the transformation x = (f + c) * (d + b). These transformations (options 4, 5 and 6) are not decomposition. For option 7, after the transformation x = f * b + c. Option 7 is a self-synchronization decomposition. In this case, the inverter is selected as a separate element, corresponding to the switching on signal including the implicants. A similar result is achieved in two steps with the help of the above transformations. First, the inclusive implicant is allocated, then it is allocated the input inverter of the enable signal. For option 1, after the transformation x = f + b * c. Option 1 is also a self-synchronization decomposition. This is a special case of option 7, when including the implicant consists of a single signal.
We systematize the results. For the model under consideration, with the decomposition of the logical function NOT-AND-OR to maintain self-synchronization, only the following transformations are possible - the selection as a separate element:
1 - one or more, starting from the including, overlapping implicant (a special case is for the function NOT-OR selection of several overlapping signals, starting from the including);
2 - in the including several implicant, starting from the including, overlapping signals;
3 - input inverter corresponding to the switching on signal including implicants (a special case is for the NOT-OR function selecting the input inverter corresponding to the turning on signal).
These transformations do not allow the implicant to be included if it was not prior to the conversion. Hence the conclusion: if a logical function contains an implicant that consists of more than one signal and is not inclusive, such a function cannot be fragmented using decomposition that preserves self-synchronization, down to two-input elements. Any logical NOT-AND-OR function for which more than one variable contains only an implicant that can be included can be split up to two-input elements (2I-NO, 2ILE-NO) with the help of decomposition preserving self-synchronization.
Step 1 - if the logical element contains only one implicant (or all implicants consist of one variable) go to step 3, otherwise go to step 2.
Step 2 - we select as a separate element all implicants, except for one, starting from including. Next, work with the newly received element. Go to step 1.
Step 3 - if the element consists of two variables, go to step 5, otherwise proceed to step 4.
Step 4 - select as a separate element all variables, except for one, starting from including. Next, work with the newly received element. Go to step 3.
Step 5 - applies to all received two-input elements.
Step 5.1 - if the input inverters on both inputs, convert the element to dual.
Step 5.2 - if the input inverter is one and corresponds to a signal that is not inclusive, convert the element to dual.
Step 5.3 - input inverter, if any, select as a separate element. Crushing is complete.
Now back to formula 1 at the beginning of the text. If the implicant x * f is missing in a logical expression, then the function looks like this: x = a * b * c + g + h + i. Her behavior:
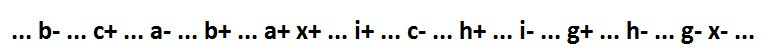
As can be seen, the only implicant consisting of more than one variable (a * b * c) is inclusive. And this function with the help of decomposition can be fragmented to the minimum components while maintaining self-synchronization.
If the implicant x * f is present in a logical expression, then the function looks like this: x = a * b * c + x * f + g + h + i. Her behavior:
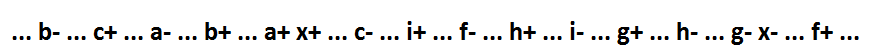
An implicant x * f, which is not inclusive, consists of more than one variable. Such a function cannot be fragmented while maintaining self-synchronization. But apply a self-synchronous transformation: add a signal y - dual to the signal x. Adding a signal y changes the function of only the signal x and the signal whose switching was a consequence of the x- event (the variable x is replaced with the variable y).
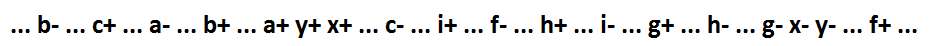
Now x = (f + i + h + g) * y, y = c * b * a + x. The implicants f + i + h + g and c * b * a include and, accordingly, the functions x and y can be fragmented to minimum components while maintaining self-synchronization.
A simplified model of behavior (without parallelism, choice, and multiple signals) allows us to identify properties naturally inherent in binary processes. Synthesis of self-timed circuits in a minimal basis is a natural phenomenon that does not require any design.
Source: https://habr.com/ru/post/444780/
All Articles